【期末真题】河南省周口市2023-2024学年度下期期末质量监测七年级数学(含答案)
文档属性
| 名称 | 【期末真题】河南省周口市2023-2024学年度下期期末质量监测七年级数学(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 578.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-10 20:29:06 | ||
图片预览



文档简介
2023-2024学年度下期期末质量监测
七年级数学
注意事项:
本试卷共6页,三个大题,满分120分,考试时间100分钟。
本试卷上不要答题,请按答题卡上注意事项的要求直接把答案填写在答题卡上。答在试卷上的答案无效。
选择题(每小题3分,共30分)下列个小题均有四个答案,其中只有一个是正确的。
1.下列关于的判断正确的是( )
A. -3>0 B . -2<0 C.2> D. <3
2.如图是光的反射规律示意图,CO是入射光线,OD是反射光线,OE是法线,EO⊥AB,∠EOD反射角,∠COE=∠EOD,若∠AOC=2∠EOD,则入射角∠COE的度数为( )
A.30° B.40°
C.45° D.60°
3.点P在第二象限,P到轴的距离为2,到轴的距离为3,则点P的坐标是( )
A.(-2,3) B. (-3,2) C. (3,-2) D. (2,-3)
4.解为 的方程组可以是( )
A. B. C. D.
5.已知,则下列不等式不成立的是( )
A. B. C. D.
6.下列调查中,适合采用全面调查的是( )
A.检测一批灯管的使用寿命 B.检测一批汽车的抗撞击能力
C.测试2024神舟18号飞船的零件质量 D.《2024年第九季诗词大会》的收视率
7.我国明代数学读本《算法统宗》有一道题,其题意为:客人一起分银子,若每人7两,还剩4两,若每人9两,还差8两.若客人为人,银子为两,则方程组为( )
A. B. C. D.
8.把变形成用表示的形式为( )
A. B. C. D.
9.下列说法正确的是( )
A.是不等式的一个解 B. 是不等式的解集
C. 是不等式的唯一解 D. 不是不等式的解
10.如图,在平面直角坐标系中,某点P从原点O出发,向右平移2个单位长度到达,再向上平移4个单位长度到达,再向左平移6个单位长度到达,再向下平移8个单位长度到达,再向右平移10个单位长度到达···,按此规律进行下去,点的坐标是( )
A.(-24,-24) B.(-12,-12)
C.(-24,24) D.(-12,12)
二、填空题(每小题3分,共15分)
11.请写出满足条件的一个无理数 .
12.在平面直角坐标系O中,将线段AB平移后得到线段,点(1,2)的对应点A’的坐标为(-1,-2),则点B(1,6)的对应点B’的坐标为 .
13.已知是关于,的二元一次方程组的解,则a+3b的立方根为 .
14.为了解某学校1500名学生的视力情况,从这些学生的视力评估报告中,简单随机抽取了300名学生的报告进行统计分析,以下说法:①1500名学生的视力情况是总体;②300名学生的视力情况是个体;③1500名学生的视力评估报告可以组成5个样本;④样本容量是300.其中正确的是 .
15.三个连续的正整数之和小于2024,这样的正整数有 组.
三、解答题(本大题共8个小题,满分75题)
16.(10分)
(1)计算:;
(2)已知,求的值.
17.(10分)用适当的方法解方程组:
(1)
(2)
18.(10分)
(1)解不等式,并写出最大整数解;
(2)解不等式,利用数轴确定不等式的解集.
19.(9分)如图,DE∥BC,BE平分∠ABC,∠ADE=50°,∠C=70°,求∠BEC的度数。
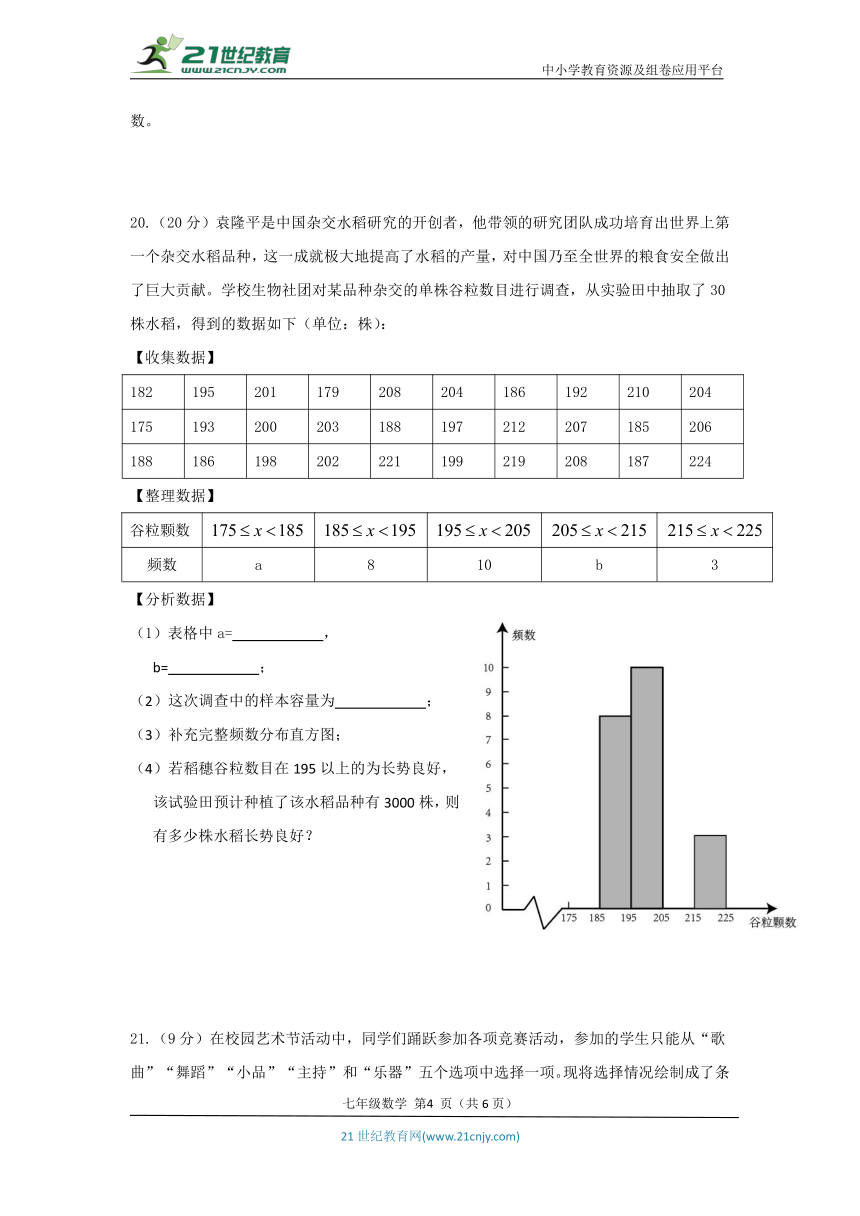
20.(20分)袁隆平是中国杂交水稻研究的开创者,他带领的研究团队成功培育出世界上第一个杂交水稻品种,这一成就极大地提高了水稻的产量,对中国乃至全世界的粮食安全做出了巨大贡献。学校生物社团对某品种杂交的单株谷粒数目进行调查,从实验田中抽取了30株水稻,得到的数据如下(单位:株):
【收集数据】
182 195 201 179 208 204 186 192 210 204
175 193 200 203 188 197 212 207 185 206
188 186 198 202 221 199 219 208 187 224
【整理数据】
谷粒颗数
频数 a 8 10 b 3
【分析数据】
(1)表格中a= , b= ;
(2)这次调查中的样本容量为 ;
(3)补充完整频数分布直方图;
(4)若稻穗谷粒数目在195以上的为长势良好,该试验田预计种植了该水稻品种有3000株,则有多少株水稻长势良好?
21.(9分)在校园艺术节活动中,同学们踊跃参加各项竞赛活动,参加的学生只能从“歌曲”“舞蹈”“小品”“主持”和“乐器”五个选项中选择一项。现将选择情况绘制成了条形统计图和不完整的扇形统计图如图所示,其中条形统计图部分被不小心污染,请根据统计图中的相关信息,回答下列问题:
(1)参加“主持”比赛的人数是参加“乐器”比赛人数的 倍;
(2)在图2中,“小品”部分所对应的圆心角的度数为 度;
(3)参加比赛活动的学生有50%将会获奖,奖项共设3个等次,其中一等奖与二等奖人数之比为1∶2,获三等奖的人数比获一等奖人数多50人,获一、二、三等奖的学生各有多少人?
22.(9分)根据等式和不等式的基本性质,我们可以得到比较两数大小的方法:
若,则;若,则;若,则。反之也成立,这种比较大小的方法称为“作差法比较大小”。
(1)若,则a-3 6+3(填“>”、“=”或“<”)
(2)若,,试比较M,N的大小,并说明理由。
23.(9分)为拓宽学生视野,传承优秀传统文化,我市某中学决定组织部分师生去老子故里开展研学活动,参加此次活动的师生,若每位老师带14名学生,则还剩10名学生没老师带;若每位老师带15名学生,就有一位老师少带6名学生。现有甲、乙两种客车,它们的载客量和租金如下表所示:
甲型客车 乙型客车
载客量(人辆) 35 30
租金(元/辆) 4000 3400
(1)参加此次研学活动的老师和学生各有多少人?
(2)为安全起见,要保证每辆车上至少要有2名老师,则租车总数最多 辆;
(3)在(2)的基础上,学校计划租用最多的客车,且这次研学活动的租车总费用不能超过3万元,你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由。
参考答案
选择题
D
A
B
C
D
C
B
A
A
B
二、填空题
11.
12.(-1,2)
13. 2
14.①④
15. 673
三、解答题
16.(1) (2)-8或12
17. (1) (2)
18.(1) (2)
19. 85°
20.(1)3 6 (2)30 (3)19000
21.(1)3 (2)86.4 (3)获得一、二、三等奖的人数分别为25人、50人、75人
22.(1)>
(2)
>0,所以M>N
23.(1) 学生234人,老师16人
(2)8
(3)有3种不同的租车方案
①租2辆甲型客车,6辆乙型客车,共花费4000×2+3400×6=28400(元)
②租3辆甲型客车,5辆乙型客车,共花费4000×3+3400×5=29000(元)
③租4辆甲型客车,4辆乙型客车,共花费4000×4+3400×4=29600(元)
种租车方案最省钱。
中小学教育资源及组卷应用平台
七年级数学 第8 页(共6页)
21世纪教育网(www.21cnjy.com)
七年级数学
注意事项:
本试卷共6页,三个大题,满分120分,考试时间100分钟。
本试卷上不要答题,请按答题卡上注意事项的要求直接把答案填写在答题卡上。答在试卷上的答案无效。
选择题(每小题3分,共30分)下列个小题均有四个答案,其中只有一个是正确的。
1.下列关于的判断正确的是( )
A. -3>0 B . -2<0 C.2> D. <3
2.如图是光的反射规律示意图,CO是入射光线,OD是反射光线,OE是法线,EO⊥AB,∠EOD反射角,∠COE=∠EOD,若∠AOC=2∠EOD,则入射角∠COE的度数为( )
A.30° B.40°
C.45° D.60°
3.点P在第二象限,P到轴的距离为2,到轴的距离为3,则点P的坐标是( )
A.(-2,3) B. (-3,2) C. (3,-2) D. (2,-3)
4.解为 的方程组可以是( )
A. B. C. D.
5.已知,则下列不等式不成立的是( )
A. B. C. D.
6.下列调查中,适合采用全面调查的是( )
A.检测一批灯管的使用寿命 B.检测一批汽车的抗撞击能力
C.测试2024神舟18号飞船的零件质量 D.《2024年第九季诗词大会》的收视率
7.我国明代数学读本《算法统宗》有一道题,其题意为:客人一起分银子,若每人7两,还剩4两,若每人9两,还差8两.若客人为人,银子为两,则方程组为( )
A. B. C. D.
8.把变形成用表示的形式为( )
A. B. C. D.
9.下列说法正确的是( )
A.是不等式的一个解 B. 是不等式的解集
C. 是不等式的唯一解 D. 不是不等式的解
10.如图,在平面直角坐标系中,某点P从原点O出发,向右平移2个单位长度到达,再向上平移4个单位长度到达,再向左平移6个单位长度到达,再向下平移8个单位长度到达,再向右平移10个单位长度到达···,按此规律进行下去,点的坐标是( )
A.(-24,-24) B.(-12,-12)
C.(-24,24) D.(-12,12)
二、填空题(每小题3分,共15分)
11.请写出满足条件的一个无理数 .
12.在平面直角坐标系O中,将线段AB平移后得到线段,点(1,2)的对应点A’的坐标为(-1,-2),则点B(1,6)的对应点B’的坐标为 .
13.已知是关于,的二元一次方程组的解,则a+3b的立方根为 .
14.为了解某学校1500名学生的视力情况,从这些学生的视力评估报告中,简单随机抽取了300名学生的报告进行统计分析,以下说法:①1500名学生的视力情况是总体;②300名学生的视力情况是个体;③1500名学生的视力评估报告可以组成5个样本;④样本容量是300.其中正确的是 .
15.三个连续的正整数之和小于2024,这样的正整数有 组.
三、解答题(本大题共8个小题,满分75题)
16.(10分)
(1)计算:;
(2)已知,求的值.
17.(10分)用适当的方法解方程组:
(1)
(2)
18.(10分)
(1)解不等式,并写出最大整数解;
(2)解不等式,利用数轴确定不等式的解集.
19.(9分)如图,DE∥BC,BE平分∠ABC,∠ADE=50°,∠C=70°,求∠BEC的度数。
20.(20分)袁隆平是中国杂交水稻研究的开创者,他带领的研究团队成功培育出世界上第一个杂交水稻品种,这一成就极大地提高了水稻的产量,对中国乃至全世界的粮食安全做出了巨大贡献。学校生物社团对某品种杂交的单株谷粒数目进行调查,从实验田中抽取了30株水稻,得到的数据如下(单位:株):
【收集数据】
182 195 201 179 208 204 186 192 210 204
175 193 200 203 188 197 212 207 185 206
188 186 198 202 221 199 219 208 187 224
【整理数据】
谷粒颗数
频数 a 8 10 b 3
【分析数据】
(1)表格中a= , b= ;
(2)这次调查中的样本容量为 ;
(3)补充完整频数分布直方图;
(4)若稻穗谷粒数目在195以上的为长势良好,该试验田预计种植了该水稻品种有3000株,则有多少株水稻长势良好?
21.(9分)在校园艺术节活动中,同学们踊跃参加各项竞赛活动,参加的学生只能从“歌曲”“舞蹈”“小品”“主持”和“乐器”五个选项中选择一项。现将选择情况绘制成了条形统计图和不完整的扇形统计图如图所示,其中条形统计图部分被不小心污染,请根据统计图中的相关信息,回答下列问题:
(1)参加“主持”比赛的人数是参加“乐器”比赛人数的 倍;
(2)在图2中,“小品”部分所对应的圆心角的度数为 度;
(3)参加比赛活动的学生有50%将会获奖,奖项共设3个等次,其中一等奖与二等奖人数之比为1∶2,获三等奖的人数比获一等奖人数多50人,获一、二、三等奖的学生各有多少人?
22.(9分)根据等式和不等式的基本性质,我们可以得到比较两数大小的方法:
若,则;若,则;若,则。反之也成立,这种比较大小的方法称为“作差法比较大小”。
(1)若,则a-3 6+3(填“>”、“=”或“<”)
(2)若,,试比较M,N的大小,并说明理由。
23.(9分)为拓宽学生视野,传承优秀传统文化,我市某中学决定组织部分师生去老子故里开展研学活动,参加此次活动的师生,若每位老师带14名学生,则还剩10名学生没老师带;若每位老师带15名学生,就有一位老师少带6名学生。现有甲、乙两种客车,它们的载客量和租金如下表所示:
甲型客车 乙型客车
载客量(人辆) 35 30
租金(元/辆) 4000 3400
(1)参加此次研学活动的老师和学生各有多少人?
(2)为安全起见,要保证每辆车上至少要有2名老师,则租车总数最多 辆;
(3)在(2)的基础上,学校计划租用最多的客车,且这次研学活动的租车总费用不能超过3万元,你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由。
参考答案
选择题
D
A
B
C
D
C
B
A
A
B
二、填空题
11.
12.(-1,2)
13. 2
14.①④
15. 673
三、解答题
16.(1) (2)-8或12
17. (1) (2)
18.(1) (2)
19. 85°
20.(1)3 6 (2)30 (3)19000
21.(1)3 (2)86.4 (3)获得一、二、三等奖的人数分别为25人、50人、75人
22.(1)>
(2)
>0,所以M>N
23.(1) 学生234人,老师16人
(2)8
(3)有3种不同的租车方案
①租2辆甲型客车,6辆乙型客车,共花费4000×2+3400×6=28400(元)
②租3辆甲型客车,5辆乙型客车,共花费4000×3+3400×5=29000(元)
③租4辆甲型客车,4辆乙型客车,共花费4000×4+3400×4=29600(元)
种租车方案最省钱。
中小学教育资源及组卷应用平台
七年级数学 第8 页(共6页)
21世纪教育网(www.21cnjy.com)
同课章节目录
