2.2.1用样本的频率分布估计总体分布
文档属性
| 名称 | 2.2.1用样本的频率分布估计总体分布 |

|
|
| 格式 | rar | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-09-13 00:00:00 | ||
图片预览



文档简介
课件29张PPT。2.2.1用样本的频率分布
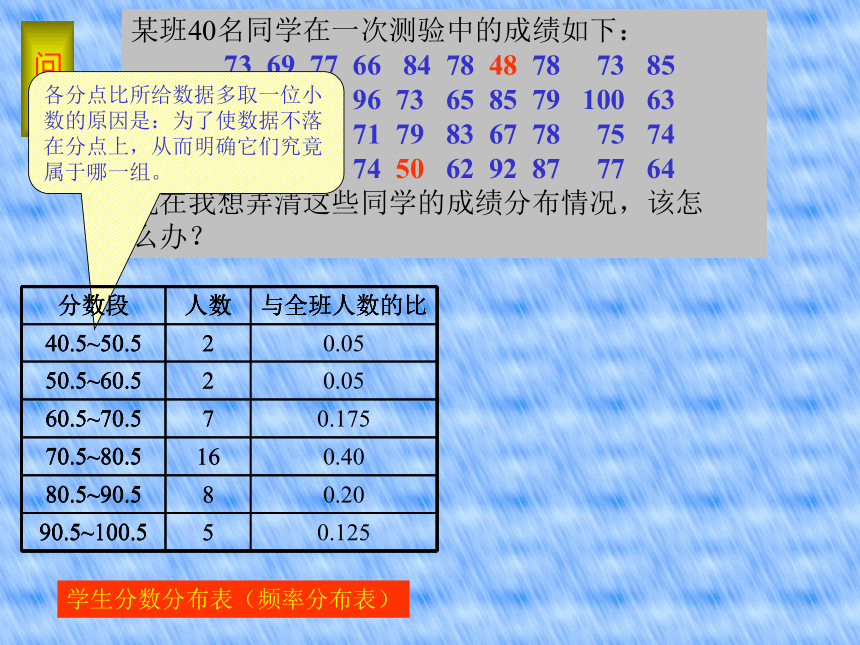
估计总体分布问题某班40名同学在一次测验中的成绩如下:
73 69 77 66 84 78 48 78 73 85
98 81 52 96 73 65 85 79 100 63
88 57 99 71 79 83 67 78 75 74
71 89 76 74 50 62 92 87 77 64
现在我想弄清这些同学的成绩分布情况,该怎
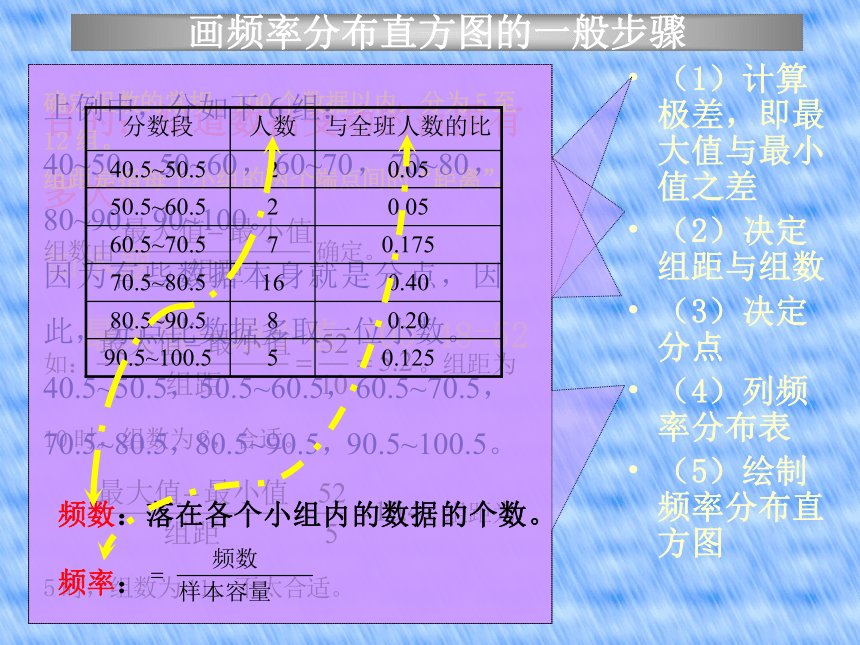
么办? 各分点比所给数据多取一位小数的原因是:为了使数据不落在分点上,从而明确它们究竟属于哪一组。学生分数分布表(频率分布表)(1)计算极差,即最大值与最小值之差
(2)决定组距与组数
(3)决定分点
(4)列频率分布表
(5)绘制频率分布直方图画频率分布直方图的一般步骤一、求极差,即数据中最大值与最小值的差二、决定组距与组数 :组距=极差/组数三、分组,通常对组内数值所在区间,
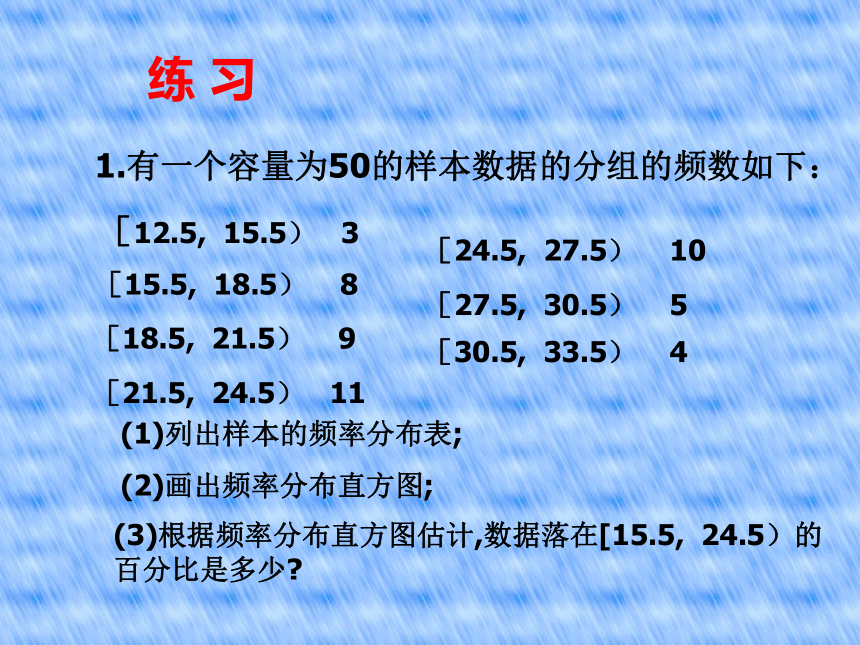
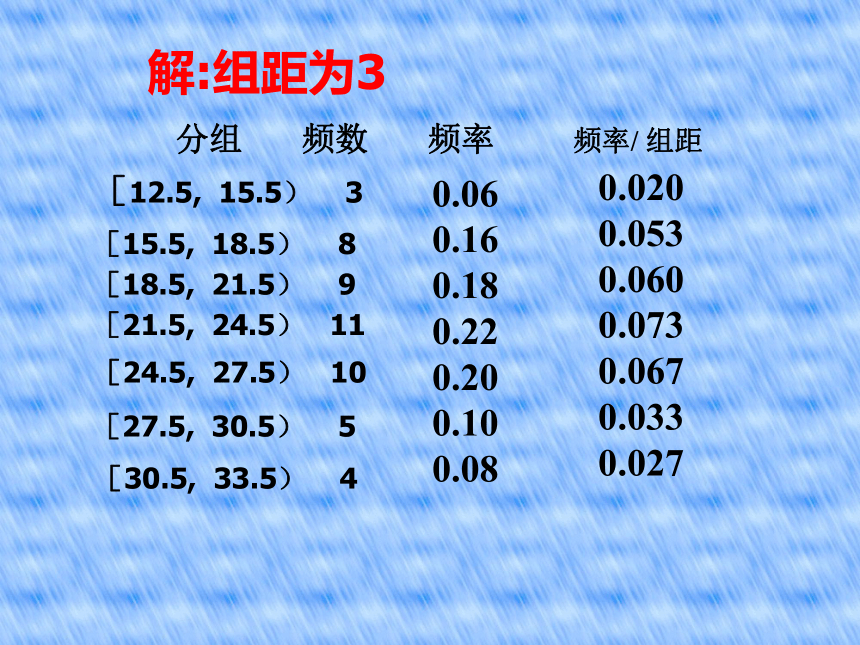
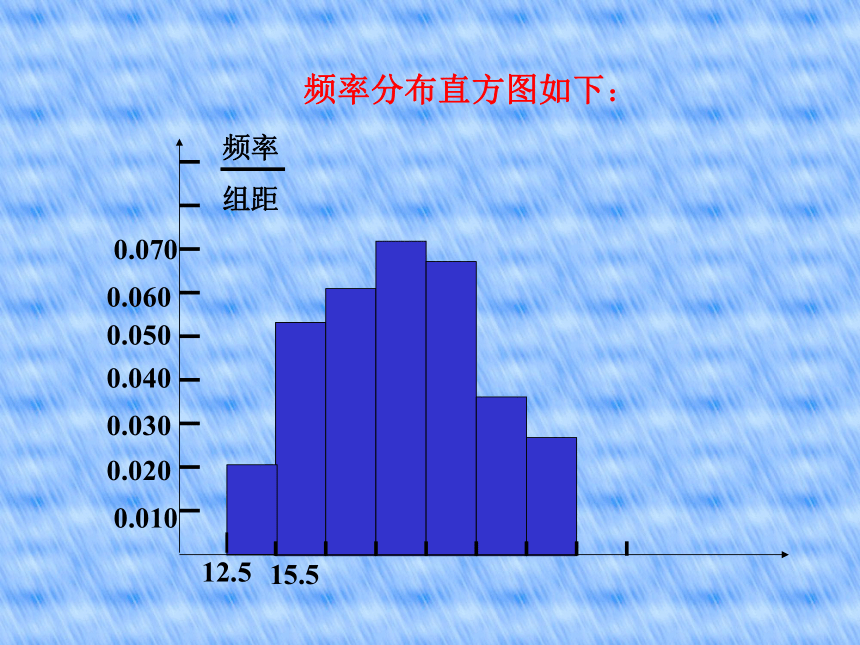
取左闭右开区间 , 最后一组取闭区间四、登记频数,计算频率,列出频率分布表画一组数据的频率分布直方图,可以按以下的步骤进行:五、画出频率分布直方图(纵轴表示频率/组距)练 习1.有一个容量为50的样本数据的分组的频数如下:[12.5, 15.5) 3[15.5, 18.5) 8[18.5, 21.5) 9[21.5, 24.5) 11[24.5, 27.5) 10[27.5, 30.5) 5[30.5, 33.5) 4(1)列出样本的频率分布表;(2)画出频率分布直方图;(3)根据频率分布直方图估计,数据落在[15.5, 24.5)的百分比是多少? 解:组距为3 分组 频数 频率 频率/ 组距[12.5, 15.5) 3[15.5, 18.5) 8[18.5, 21.5) 9[21.5, 24.5) 11[24.5, 27.5) 10[27.5, 30.5) 5[30.5, 33.5) 40.06
0.16
0.18
0.22
0.20
0.10
0.080.020
0.053
0.060
0.073
0.067
0.033
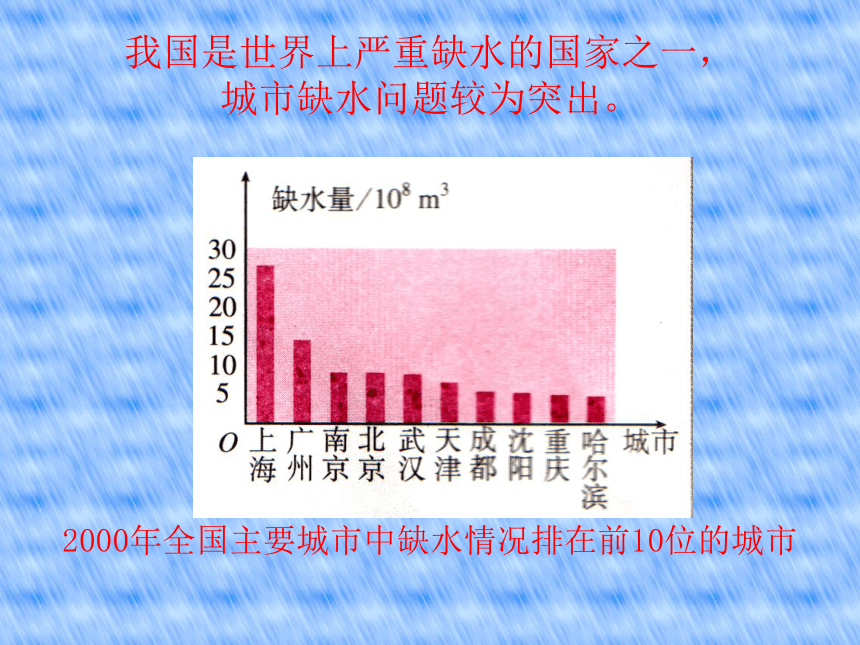
0.027频率分布直方图如下:0.0100.0200.0300.0400.05012.515.50.0600.070我国是世界上严重缺水的国家之一, 城市缺水问题较为突出。2000年全国主要城市中缺水情况排在前10位的城市 某市政府为了节约生活用水,计划在本市试行居
民生活用水定额管理,即确定一个居民月用水量
标准a , 用水量不超过a的部分按平价收费,超过a
的部分按议价收费。 ①如果希望大部分居民的日常生活不受影响,那 么标准a定为多少比较合理呢? ②为了较合理地确定这个标准,你认为需要做
哪些工作? 通过抽样,我们获得了100位居民某年的月均用 水量(单位:t) ,如下表: 思考:由上表,大家可以得到什么信息? 1.求极差: 步骤: 频率分布直方图 2.决定组距与组数 :组数= 4.3 - 0.2 = 4.13.将数据分组[0,0.5 ),[0.5,1 ),…,[4,4.5] 4.列频率分布表100位居民月均用水量的频率分布表5.画频率分布直方图
小长方形的面积=?频率分布直方图如下:
小长方形的面积总和=?注:小长方形的面积=组距×频率/组距=频率
各长方形的面积总和等于1。频率分布直方图如下:
月均用水量最多的在那个区间?图2.2-2 100位居民的月均用水量的频率分布折线图
频率分布折线图:连接频率分布直方图中各小长方形上 端
的中点,就得到频率分布折线图。探究:
同样一组数据,如果组距不同,横轴、纵轴的单位不同,得到的图的形状也会不同。不同的形状给人以不同的印象,这种印象有时会影响我们对总体的判断。分别以1和0.1为组距重新作图,然后谈谈你对图的印象。 ※总体密度曲线能够很好的反映总体在各个范围内的百分比,能构提供更准确的信息。尽管有些总体密度曲线是客观存在的,但是很难象函数图象那样准确的地画出来。
?思考一下图中阴影部分的面积表示什么? 用样本分布直方图去估计相应的总体分布时,一般样本容量越大,频率分布直方图就会无限接近总体密度曲线,就越精确地反映了总体的分布规律,即越精确地反映了总体在各个范围内取值百分比。 总体密度曲线反映了总体在各个范围内取值的百分比,精确地反映了总体的分布规律。是研究总体分布的工具.总体密度曲线练习:从一种零件中抽取了80件,尺寸数据表示如下(单位:cm):
?
?
?
?
?
?
这里用x×n表示有n件尺寸为x的零件,如362.51×1表示有1件尺寸为362.51cm的零件。作出样本的频率分布表和频率分布直方图。 想一想茎叶图某赛季甲、乙两名篮球运动员每场比赛得分的原始记录如下:(1)甲运动员得分:
13,51,23,8,26,38,16,33,14,28,39(1)乙运动员得分: 49,24,12,31,50,31,44,36,15,37,25,36,39茎叶图甲乙0
1
2
3
4
5
2 5
5 4
1 6 1 6 7 9
4 9
08
4 6 3
6 8
3 8 9
1 叶就是从茎的旁边生长出来的数,表示得分的个位数。 茎是指中间的一列数,表示得分的十位数 茎叶图不仅能够保留原始数据,而且能够展示数据的分布情况。
从运动员的成绩的分布来看,乙运动员的成绩更好;从叶在茎上的分布情况来看,乙运动员的得分更集中于峰值附近,说明乙运动员的发挥更稳定。
在样本数据较少时,用茎叶图表示数据的效果较好。它不但可以保留所有信息,而且可以随时纪录,这对数据的纪录和表示都能带来方便。但当样本数据较多时,茎叶图就显得不太方便。因为每一个数据都要在茎叶图中占据一个空间,如果数据很多,枝叶就会很长。 小结:思考 :
如果当地政府希望使 85% 以上的居民每月的用水量不超出标准,根据频率分布表和频率分布直方图,你能对制定月用水量标准提出建议吗? 频率分布直方图应用1.求极差2.决定组距与组数3.将数据分组4.列频率分布表5.画频率分布直方图再见!
估计总体分布问题某班40名同学在一次测验中的成绩如下:
73 69 77 66 84 78 48 78 73 85
98 81 52 96 73 65 85 79 100 63
88 57 99 71 79 83 67 78 75 74
71 89 76 74 50 62 92 87 77 64
现在我想弄清这些同学的成绩分布情况,该怎
么办? 各分点比所给数据多取一位小数的原因是:为了使数据不落在分点上,从而明确它们究竟属于哪一组。学生分数分布表(频率分布表)(1)计算极差,即最大值与最小值之差
(2)决定组距与组数
(3)决定分点
(4)列频率分布表
(5)绘制频率分布直方图画频率分布直方图的一般步骤一、求极差,即数据中最大值与最小值的差二、决定组距与组数 :组距=极差/组数三、分组,通常对组内数值所在区间,
取左闭右开区间 , 最后一组取闭区间四、登记频数,计算频率,列出频率分布表画一组数据的频率分布直方图,可以按以下的步骤进行:五、画出频率分布直方图(纵轴表示频率/组距)练 习1.有一个容量为50的样本数据的分组的频数如下:[12.5, 15.5) 3[15.5, 18.5) 8[18.5, 21.5) 9[21.5, 24.5) 11[24.5, 27.5) 10[27.5, 30.5) 5[30.5, 33.5) 4(1)列出样本的频率分布表;(2)画出频率分布直方图;(3)根据频率分布直方图估计,数据落在[15.5, 24.5)的百分比是多少? 解:组距为3 分组 频数 频率 频率/ 组距[12.5, 15.5) 3[15.5, 18.5) 8[18.5, 21.5) 9[21.5, 24.5) 11[24.5, 27.5) 10[27.5, 30.5) 5[30.5, 33.5) 40.06
0.16
0.18
0.22
0.20
0.10
0.080.020
0.053
0.060
0.073
0.067
0.033
0.027频率分布直方图如下:0.0100.0200.0300.0400.05012.515.50.0600.070我国是世界上严重缺水的国家之一, 城市缺水问题较为突出。2000年全国主要城市中缺水情况排在前10位的城市 某市政府为了节约生活用水,计划在本市试行居
民生活用水定额管理,即确定一个居民月用水量
标准a , 用水量不超过a的部分按平价收费,超过a
的部分按议价收费。 ①如果希望大部分居民的日常生活不受影响,那 么标准a定为多少比较合理呢? ②为了较合理地确定这个标准,你认为需要做
哪些工作? 通过抽样,我们获得了100位居民某年的月均用 水量(单位:t) ,如下表: 思考:由上表,大家可以得到什么信息? 1.求极差: 步骤: 频率分布直方图 2.决定组距与组数 :组数= 4.3 - 0.2 = 4.13.将数据分组[0,0.5 ),[0.5,1 ),…,[4,4.5] 4.列频率分布表100位居民月均用水量的频率分布表5.画频率分布直方图
小长方形的面积=?频率分布直方图如下:
小长方形的面积总和=?注:小长方形的面积=组距×频率/组距=频率
各长方形的面积总和等于1。频率分布直方图如下:
月均用水量最多的在那个区间?图2.2-2 100位居民的月均用水量的频率分布折线图
频率分布折线图:连接频率分布直方图中各小长方形上 端
的中点,就得到频率分布折线图。探究:
同样一组数据,如果组距不同,横轴、纵轴的单位不同,得到的图的形状也会不同。不同的形状给人以不同的印象,这种印象有时会影响我们对总体的判断。分别以1和0.1为组距重新作图,然后谈谈你对图的印象。 ※总体密度曲线能够很好的反映总体在各个范围内的百分比,能构提供更准确的信息。尽管有些总体密度曲线是客观存在的,但是很难象函数图象那样准确的地画出来。
?思考一下图中阴影部分的面积表示什么? 用样本分布直方图去估计相应的总体分布时,一般样本容量越大,频率分布直方图就会无限接近总体密度曲线,就越精确地反映了总体的分布规律,即越精确地反映了总体在各个范围内取值百分比。 总体密度曲线反映了总体在各个范围内取值的百分比,精确地反映了总体的分布规律。是研究总体分布的工具.总体密度曲线练习:从一种零件中抽取了80件,尺寸数据表示如下(单位:cm):
?
?
?
?
?
?
这里用x×n表示有n件尺寸为x的零件,如362.51×1表示有1件尺寸为362.51cm的零件。作出样本的频率分布表和频率分布直方图。 想一想茎叶图某赛季甲、乙两名篮球运动员每场比赛得分的原始记录如下:(1)甲运动员得分:
13,51,23,8,26,38,16,33,14,28,39(1)乙运动员得分: 49,24,12,31,50,31,44,36,15,37,25,36,39茎叶图甲乙0
1
2
3
4
5
2 5
5 4
1 6 1 6 7 9
4 9
08
4 6 3
6 8
3 8 9
1 叶就是从茎的旁边生长出来的数,表示得分的个位数。 茎是指中间的一列数,表示得分的十位数 茎叶图不仅能够保留原始数据,而且能够展示数据的分布情况。
从运动员的成绩的分布来看,乙运动员的成绩更好;从叶在茎上的分布情况来看,乙运动员的得分更集中于峰值附近,说明乙运动员的发挥更稳定。
在样本数据较少时,用茎叶图表示数据的效果较好。它不但可以保留所有信息,而且可以随时纪录,这对数据的纪录和表示都能带来方便。但当样本数据较多时,茎叶图就显得不太方便。因为每一个数据都要在茎叶图中占据一个空间,如果数据很多,枝叶就会很长。 小结:思考 :
如果当地政府希望使 85% 以上的居民每月的用水量不超出标准,根据频率分布表和频率分布直方图,你能对制定月用水量标准提出建议吗? 频率分布直方图应用1.求极差2.决定组距与组数3.将数据分组4.列频率分布表5.画频率分布直方图再见!
