1.3位置变化快慢的描述—速度 课件(共31张PPT)2024-2025学年高一上学期物理人教版(2019)必修第一册
文档属性
| 名称 | 1.3位置变化快慢的描述—速度 课件(共31张PPT)2024-2025学年高一上学期物理人教版(2019)必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 562.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-07-10 10:51:38 | ||
图片预览









文档简介
(共31张PPT)
1.3位置变化快慢的描述 ---- 速度
第一课时
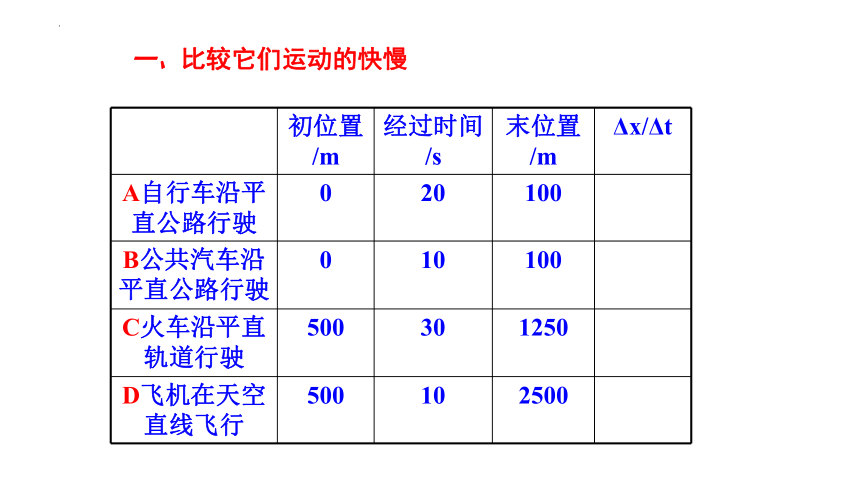
一、比较它们运动的快慢
初位置/m 经过时间/s 末位置/m Δx/Δt
A自行车沿平直公路行驶 0 20 100
B公共汽车沿平直公路行驶 0 10 100
C火车沿平直轨道行驶 500 30 1250
D飞机在天空直线飞行 500 10 2500
总结
比较运动快慢有两种方法:一是在位移相同的情况下,看所用时间的长短;二是在时间相同的情况下,看位移的大小。
若位移不相同,时间也不相同时,那如何去比较呢?
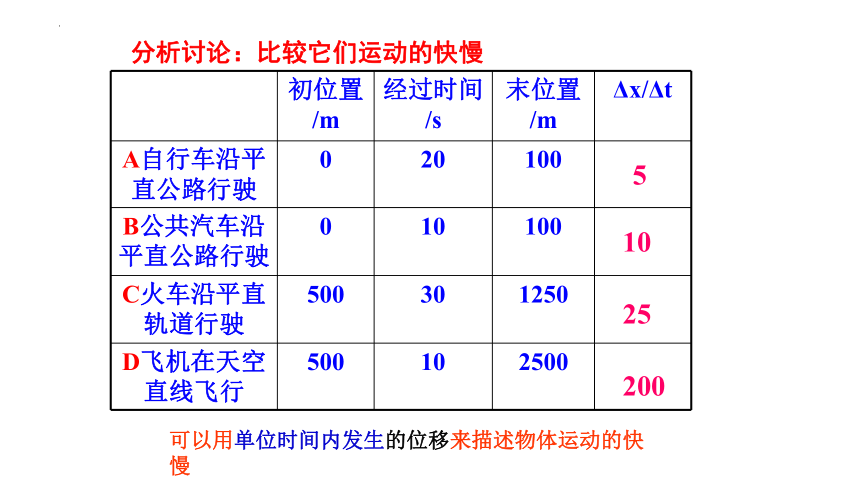
分析讨论:比较它们运动的快慢
初位置/m 经过时间/s 末位置/m Δx/Δt
A自行车沿平直公路行驶 0 20 100
B公共汽车沿平直公路行驶 0 10 100
C火车沿平直轨道行驶 500 30 1250
D飞机在天空直线飞行 500 10 2500
5
10
25
200
可以用单位时间内发生的位移来描述物体运动的快慢
知识生成:1.物理学中用位移 Δx 与发生这段位移所用_________的比值来表示物体运动的快慢,这就是速度,即速度 v= ____ 。
2.在国际单位制中,速度的单位是 ,符号 或 。常用的单位还有千米每时(km/h 或km·h -1)、厘米每秒(cm/s 或 cm s 1 )。1m/s= km/h 。
3.速度是_______,既有大小,又有方向,速度的方向与时间 Δt 内的 方向相同。
问题探究:
(1) 物理学中速度是如何定义的?
(2)物体沿直线运动,位移越大,其速度是否越大?
(3)既然速度 v=Δx/Δt,其中位移是有方向的矢量,那速度有方向吗?它的方向如何确定?
二、平均速度和瞬时速度
情境引入:
某同学研究小球从斜槽滚下,依次通过O、 A 、 B、 C四点时记录的数据如图1所示。
问题引领:1. OA 、A B 、 BC三段中,小球在哪一段运动得最快?
2.分别求出 OA 、 OB、 OC 段的平均速度。你认为 O 点的瞬时速度最接近哪一段的平均速度?
3.如果从 O点起取几段更小的位移,比如 OA1、OA2 、OA3 、OA,如右图所示,哪一段的平均速度更接近 O点的瞬时速度呢?
问题:对变速运动,在相等的时间内位移不相等,所以它没有恒定的速度,怎样来描述它运动的快慢呢?
平均速度
1、定义:在变速直线运动中,运动物体的位移和通过这段位移所用时间的比值叫做这段时间内(或这段位移内)的平均速度。
矢量性:方向与这段时间内发生的位移方向相同。
物理意义:反映做变速直线运动的物体在某段时间内运动的平均快慢程度,是对变速直线运动的粗略描述。
瞬时速度:
(1)物体在某一时刻(或位置)时的速度。
(2)当△t非常非常小, △x/ △t 可看作某时刻(某位置)的瞬时速度。
物理意义:反映物体在某一时刻(或某一位置)时运动的快慢,能对变速运动做精确描述。
说明:匀速直线运动是___________不变的运动,在匀速运动中平均速度和瞬时速度相等。
方向:某一时刻(或位置)的运动方向
(3)速率:_____________叫做瞬时速率,通常叫做速率,瞬时速度是矢量,而速率是 。
(4)平均速率:物体通过的 与通过这一路程所用时间的比值。
瞬时速度的大小
标量
路程
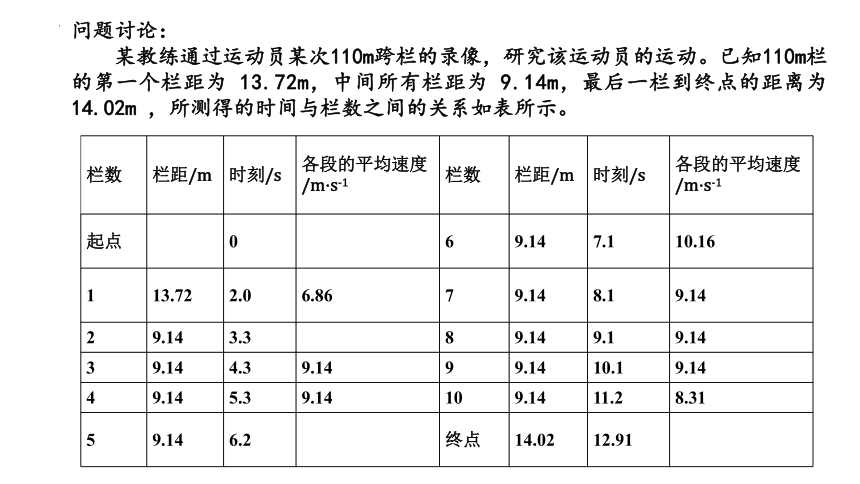
问题讨论:
某教练通过运动员某次110m跨栏的录像,研究该运动员的运动。已知110m栏的第一个栏距为 13.72m,中间所有栏距为 9.14m,最后一栏到终点的距离为 14.02m ,所测得的时间与栏数之间的关系如表所示。
栏数 栏距/m 时刻/s 各段的平均速度/m s-1 栏数 栏距/m 时刻/s 各段的平均速度/m s-1
起点 0 6 9.14 7.1 10.16
1 13.72 2.0 6.86 7 9.14 8.1 9.14
2 9.14 3.3 8 9.14 9.1 9.14
3 9.14 4.3 9.14 9 9.14 10.1 9.14
4 9.14 5.3 9.14 10 9.14 11.2 8.31
5 9.14 6.2 终点 14.02 12.91
(1)用总的位移 110m除以时间12.91s,求得的速度的物理意义是什么?
(2) 请把表中未算出来的平均速度算出来,并填入表中。
(3) 请描述该运动员在此次 110m跨栏全过程中速度的变化情况。
【例1】一辆汽车沿直线从甲地到乙地, 前一半时间的速度为60m/s,后一半时间的速度为80m/s,则:(1)全过程中的平均速度是多少? ⑵ 如果前一半位移的速度为60m/s,后一半位移的速度为80m/s,则全过程中的平均速度为多少?
⑴设一半时间为t,则由平均速度的定义式有:
解:
=70m/s
=68.6m/s
⑵设一半位移为x,则由平均速度的定义式有:
【例2】如果一位同学从操场中心A出发,向北走了40 m,到达C点,然后又向东走了30 m,共用20s到达B点,运动过程如图,该同学从A到B整个过程中的平均速率多大?平均速度多大?沿什么方向?
平均速度的方向:物体的位移方向。
3.5m/s
2.5m/s
A.物体做匀速直线运动时,速度v与运动的位移Δx成正比,与运动时间Δt成反比
B.速度v的大小与运动的位移Δx和时间Δt都无关
C.速度大小不变的运动是匀速直线运动
D.v1=2 m/s、v2=-3 m/s,因为2>-3,所以v1>v2
1、关于速度的定义式 ,以下叙述正确的是( )
巩固练习
2.下列情况中的速度,属于平均速度的是( )
A.刘翔在110米跨栏时冲过终点线时的速度为9.5m/s
B.由于堵车,汽车在通过隧道过程中的速度仅为1.2m/s
C.返回地球的太空舱落到太平洋水面时的速度为8m/s
D.子弹射到墙上时的速度为800m/s
3.(多选)以下关于瞬时速度、平均速度、平均速率的说法正确的是( )
A.瞬时速度是指物体在某一位置或某一时刻的速度
B.平均速度是物体在一段时间内各个时刻瞬时速度的平均值
C.做变速运动的物体,平均速率就是平均速度的大小
D.物体做变速运动时,平均速度是指物体通过的位移与所用时间的比值
4、小球由静止开始运动,在第1s内通过的位移为1m,在第2s内通过的位移为2m,在第3s内通过的位移为3m,在第4s内通过的位移为4m,下列描述正确的是( )
A.小球在这4s内的平均速度是2.5m/s
B.小球在3s末的瞬时速度是3m/s
C.小球在前3s内的平均速度是3m/s
D.小球在做匀加速直线运动
5、登山运动中,小张用100min由宿营地X爬到山顶Y。在山道上通过的路程是2400m,相对于X升高了1200m,如图所示。
(1)求小张由X运动到Y总的位移的大小;
(2)求小张爬山的平均速度的大小;
(3)他的朋友小李从Z点爬山,比小张晚20min开始,平均速率为0.5m/s,还比小张早20min到达山顶,问小李由Z爬到Y共通过了多少路程?
第二课时
一、测量纸带的平均速度和瞬时速度
要研究物体的运动,我们首先要准确记录物体运动快慢的信息,例如,要记录上下飞舞的蝴蝶、随风摆动的树枝、飘忽不定的风筝等的运动快慢,那就十分困难;若物体做直线运动,情况就要简单一些,但直接测定物体的速度也比较复杂,如果测量物体运动的时间和位移,再经过计算或作图来判断物体的运动情况就简便多了。打点计时器就可以记录物体运动的时间和位移。
问题:下面是某同学打出的三条纸带,拉动方向是从左向右,观察、比较三条纸带,回答下列问题:
1、哪条纸带运动最慢?
2、哪条纸带运动先快后慢?
3、哪条纸带的运动可以近似看作匀速运动?
实验步骤:
1. 将打点计时器固定在桌面上,用导线连入交流的6V电压;
2. 将纸带穿过限位孔;
3. 启动电源,拉纸带,纸带上就打出一行小点随后立即关电源
先开电源,
再拉纸带
4. 取下纸带,从能够看得清的某个点开始,往后数出若干个点,如果共有n个点,那么n个点的间隔数为n-1个,则纸带的运动时间
Δt=(n-1) ×0.02 s。
5. 用刻度尺测量出从开始计数的点到最后一个计数点间的距离Δx。
6.利用公式 计算出纸带在这段时间内的平均速度
数据处理:
D
G
0
1
2
3
计时点
T=0.02s
计数点
每隔0.02s打下一个点,每隔4个点作为一个计数点(或者说后面每5个点作为计数点)
对纸带进行测量时,不要分段测量各段的位移,正确的做法是一次测量完毕(可先统一测量点到起始测量点O之间的距离),读数时应估读的毫米的下一位。
0
1
2
3
位置 0 1 2 3
x/m 0 0.0596 0.1295 0.2096
Δx/m 0 0.0596 0.0699 0.0801
Δt/s 0 0.1 0.1 0.1
v/(m·s-1) 0.60 0.70 0.80
测平均速度:
1
2
3
4
5
D
E
Δx4
0.06s
可以取每3个点作为计数点分别计算每段的平均速度和某点的瞬时速度
Δx1
Δx2
Δx3
Δx5
A
B
C
测量瞬时速度:
位置 0 1 2 3 4 5
x/m 0 0.0342 0.0731 0.1149 0.1602 0.2096
Δx/m 0 0.0342 0.0389 0.0418 0.0453 0.0494
Δt/s 0 0.06 0.06 0.06 0.06 0.06
v/(m·s-1) 0.57 0.65 0.70 0.76 0.82
纸带上某一位置的瞬时速度,可以粗略地由包含这一位置在内的一小段位移Δx内的平均速度表示,
速度——时间图像:
1.以速度v为纵轴,时间t为横轴建立直角坐标系。
2.根据计算出的不同时刻的瞬时速度值,在坐标系中描点。
3.用 曲线把这些点连接起来就得到了一条能够描述速度v与时间t关系的图线,即v-t图像。如图所示。
平滑
作图
位置 0 1 2 3 4 5
x/m 0 0.0342 0.0731 0.1149 0.1602 0.2096
Δx/m 0 0.0342 0.0389 0.0418 0.0453 0.0494
Δt/s 0 0.06 0.06 0.06 0.06 0.06
v/(m·s-1) 0.57 0.65 0.70 0.76 0.82
(2)由图像的纵、横坐标可知任一时刻速度的大小和方向或物体的某一速度所对应的时刻。
认识图像:
(4)匀速直线运动的速度图象是一条平行于时间轴的直线.
(3)v-t图像只能描述直线运动的情况,在v-t图像中速度只有正负两个方向。
(1)图线上的“点”表示物体所处的状态,“图线”表示速度随时间的变化规律。它并不表示物体运动的轨迹。
平均速度 瞬时速度
物理意义 粗略描述运动快慢,与一段时间或一段位移相对应 精确描述运动快慢,与某一时刻或某一位置相对应
大小 (Δt极小)
方向 与位移方向相同,与运动方向不一定相同 与运动方向相同,与位移方向不一定相同
联系 1.瞬时速度为0,平均速度一定为0。平均速度为0,瞬时速度不一定为0。 2.匀速直线运动,平均速度等于瞬时速度。 3.当位移足够小或Δt足够短时可以认为平均速度等于瞬时速度。
“平均速度”与“瞬时速度”的区别
通过每段的初、末速度大小比较看出。
OA段加速,AB段匀速,BC段加速,CD段减速,DE段反向加速。
12
5
-12
5
14
18
22
t/s
v/(m·s-1)
A
B
C
D
E
问题:
例5、 (多选)若一质点从t=0开始由原点出发,其v-t图象如图所示,则该质点( )
A.当t=1 s时,离原点最远
B.当t=2 s时,离原点最远
C.当t=3 s时,回到原点
D.当t=4 s时,回到原点
BD
若为x-t图像?
1.3位置变化快慢的描述 ---- 速度
第一课时
一、比较它们运动的快慢
初位置/m 经过时间/s 末位置/m Δx/Δt
A自行车沿平直公路行驶 0 20 100
B公共汽车沿平直公路行驶 0 10 100
C火车沿平直轨道行驶 500 30 1250
D飞机在天空直线飞行 500 10 2500
总结
比较运动快慢有两种方法:一是在位移相同的情况下,看所用时间的长短;二是在时间相同的情况下,看位移的大小。
若位移不相同,时间也不相同时,那如何去比较呢?
分析讨论:比较它们运动的快慢
初位置/m 经过时间/s 末位置/m Δx/Δt
A自行车沿平直公路行驶 0 20 100
B公共汽车沿平直公路行驶 0 10 100
C火车沿平直轨道行驶 500 30 1250
D飞机在天空直线飞行 500 10 2500
5
10
25
200
可以用单位时间内发生的位移来描述物体运动的快慢
知识生成:1.物理学中用位移 Δx 与发生这段位移所用_________的比值来表示物体运动的快慢,这就是速度,即速度 v= ____ 。
2.在国际单位制中,速度的单位是 ,符号 或 。常用的单位还有千米每时(km/h 或km·h -1)、厘米每秒(cm/s 或 cm s 1 )。1m/s= km/h 。
3.速度是_______,既有大小,又有方向,速度的方向与时间 Δt 内的 方向相同。
问题探究:
(1) 物理学中速度是如何定义的?
(2)物体沿直线运动,位移越大,其速度是否越大?
(3)既然速度 v=Δx/Δt,其中位移是有方向的矢量,那速度有方向吗?它的方向如何确定?
二、平均速度和瞬时速度
情境引入:
某同学研究小球从斜槽滚下,依次通过O、 A 、 B、 C四点时记录的数据如图1所示。
问题引领:1. OA 、A B 、 BC三段中,小球在哪一段运动得最快?
2.分别求出 OA 、 OB、 OC 段的平均速度。你认为 O 点的瞬时速度最接近哪一段的平均速度?
3.如果从 O点起取几段更小的位移,比如 OA1、OA2 、OA3 、OA,如右图所示,哪一段的平均速度更接近 O点的瞬时速度呢?
问题:对变速运动,在相等的时间内位移不相等,所以它没有恒定的速度,怎样来描述它运动的快慢呢?
平均速度
1、定义:在变速直线运动中,运动物体的位移和通过这段位移所用时间的比值叫做这段时间内(或这段位移内)的平均速度。
矢量性:方向与这段时间内发生的位移方向相同。
物理意义:反映做变速直线运动的物体在某段时间内运动的平均快慢程度,是对变速直线运动的粗略描述。
瞬时速度:
(1)物体在某一时刻(或位置)时的速度。
(2)当△t非常非常小, △x/ △t 可看作某时刻(某位置)的瞬时速度。
物理意义:反映物体在某一时刻(或某一位置)时运动的快慢,能对变速运动做精确描述。
说明:匀速直线运动是___________不变的运动,在匀速运动中平均速度和瞬时速度相等。
方向:某一时刻(或位置)的运动方向
(3)速率:_____________叫做瞬时速率,通常叫做速率,瞬时速度是矢量,而速率是 。
(4)平均速率:物体通过的 与通过这一路程所用时间的比值。
瞬时速度的大小
标量
路程
问题讨论:
某教练通过运动员某次110m跨栏的录像,研究该运动员的运动。已知110m栏的第一个栏距为 13.72m,中间所有栏距为 9.14m,最后一栏到终点的距离为 14.02m ,所测得的时间与栏数之间的关系如表所示。
栏数 栏距/m 时刻/s 各段的平均速度/m s-1 栏数 栏距/m 时刻/s 各段的平均速度/m s-1
起点 0 6 9.14 7.1 10.16
1 13.72 2.0 6.86 7 9.14 8.1 9.14
2 9.14 3.3 8 9.14 9.1 9.14
3 9.14 4.3 9.14 9 9.14 10.1 9.14
4 9.14 5.3 9.14 10 9.14 11.2 8.31
5 9.14 6.2 终点 14.02 12.91
(1)用总的位移 110m除以时间12.91s,求得的速度的物理意义是什么?
(2) 请把表中未算出来的平均速度算出来,并填入表中。
(3) 请描述该运动员在此次 110m跨栏全过程中速度的变化情况。
【例1】一辆汽车沿直线从甲地到乙地, 前一半时间的速度为60m/s,后一半时间的速度为80m/s,则:(1)全过程中的平均速度是多少? ⑵ 如果前一半位移的速度为60m/s,后一半位移的速度为80m/s,则全过程中的平均速度为多少?
⑴设一半时间为t,则由平均速度的定义式有:
解:
=70m/s
=68.6m/s
⑵设一半位移为x,则由平均速度的定义式有:
【例2】如果一位同学从操场中心A出发,向北走了40 m,到达C点,然后又向东走了30 m,共用20s到达B点,运动过程如图,该同学从A到B整个过程中的平均速率多大?平均速度多大?沿什么方向?
平均速度的方向:物体的位移方向。
3.5m/s
2.5m/s
A.物体做匀速直线运动时,速度v与运动的位移Δx成正比,与运动时间Δt成反比
B.速度v的大小与运动的位移Δx和时间Δt都无关
C.速度大小不变的运动是匀速直线运动
D.v1=2 m/s、v2=-3 m/s,因为2>-3,所以v1>v2
1、关于速度的定义式 ,以下叙述正确的是( )
巩固练习
2.下列情况中的速度,属于平均速度的是( )
A.刘翔在110米跨栏时冲过终点线时的速度为9.5m/s
B.由于堵车,汽车在通过隧道过程中的速度仅为1.2m/s
C.返回地球的太空舱落到太平洋水面时的速度为8m/s
D.子弹射到墙上时的速度为800m/s
3.(多选)以下关于瞬时速度、平均速度、平均速率的说法正确的是( )
A.瞬时速度是指物体在某一位置或某一时刻的速度
B.平均速度是物体在一段时间内各个时刻瞬时速度的平均值
C.做变速运动的物体,平均速率就是平均速度的大小
D.物体做变速运动时,平均速度是指物体通过的位移与所用时间的比值
4、小球由静止开始运动,在第1s内通过的位移为1m,在第2s内通过的位移为2m,在第3s内通过的位移为3m,在第4s内通过的位移为4m,下列描述正确的是( )
A.小球在这4s内的平均速度是2.5m/s
B.小球在3s末的瞬时速度是3m/s
C.小球在前3s内的平均速度是3m/s
D.小球在做匀加速直线运动
5、登山运动中,小张用100min由宿营地X爬到山顶Y。在山道上通过的路程是2400m,相对于X升高了1200m,如图所示。
(1)求小张由X运动到Y总的位移的大小;
(2)求小张爬山的平均速度的大小;
(3)他的朋友小李从Z点爬山,比小张晚20min开始,平均速率为0.5m/s,还比小张早20min到达山顶,问小李由Z爬到Y共通过了多少路程?
第二课时
一、测量纸带的平均速度和瞬时速度
要研究物体的运动,我们首先要准确记录物体运动快慢的信息,例如,要记录上下飞舞的蝴蝶、随风摆动的树枝、飘忽不定的风筝等的运动快慢,那就十分困难;若物体做直线运动,情况就要简单一些,但直接测定物体的速度也比较复杂,如果测量物体运动的时间和位移,再经过计算或作图来判断物体的运动情况就简便多了。打点计时器就可以记录物体运动的时间和位移。
问题:下面是某同学打出的三条纸带,拉动方向是从左向右,观察、比较三条纸带,回答下列问题:
1、哪条纸带运动最慢?
2、哪条纸带运动先快后慢?
3、哪条纸带的运动可以近似看作匀速运动?
实验步骤:
1. 将打点计时器固定在桌面上,用导线连入交流的6V电压;
2. 将纸带穿过限位孔;
3. 启动电源,拉纸带,纸带上就打出一行小点随后立即关电源
先开电源,
再拉纸带
4. 取下纸带,从能够看得清的某个点开始,往后数出若干个点,如果共有n个点,那么n个点的间隔数为n-1个,则纸带的运动时间
Δt=(n-1) ×0.02 s。
5. 用刻度尺测量出从开始计数的点到最后一个计数点间的距离Δx。
6.利用公式 计算出纸带在这段时间内的平均速度
数据处理:
D
G
0
1
2
3
计时点
T=0.02s
计数点
每隔0.02s打下一个点,每隔4个点作为一个计数点(或者说后面每5个点作为计数点)
对纸带进行测量时,不要分段测量各段的位移,正确的做法是一次测量完毕(可先统一测量点到起始测量点O之间的距离),读数时应估读的毫米的下一位。
0
1
2
3
位置 0 1 2 3
x/m 0 0.0596 0.1295 0.2096
Δx/m 0 0.0596 0.0699 0.0801
Δt/s 0 0.1 0.1 0.1
v/(m·s-1) 0.60 0.70 0.80
测平均速度:
1
2
3
4
5
D
E
Δx4
0.06s
可以取每3个点作为计数点分别计算每段的平均速度和某点的瞬时速度
Δx1
Δx2
Δx3
Δx5
A
B
C
测量瞬时速度:
位置 0 1 2 3 4 5
x/m 0 0.0342 0.0731 0.1149 0.1602 0.2096
Δx/m 0 0.0342 0.0389 0.0418 0.0453 0.0494
Δt/s 0 0.06 0.06 0.06 0.06 0.06
v/(m·s-1) 0.57 0.65 0.70 0.76 0.82
纸带上某一位置的瞬时速度,可以粗略地由包含这一位置在内的一小段位移Δx内的平均速度表示,
速度——时间图像:
1.以速度v为纵轴,时间t为横轴建立直角坐标系。
2.根据计算出的不同时刻的瞬时速度值,在坐标系中描点。
3.用 曲线把这些点连接起来就得到了一条能够描述速度v与时间t关系的图线,即v-t图像。如图所示。
平滑
作图
位置 0 1 2 3 4 5
x/m 0 0.0342 0.0731 0.1149 0.1602 0.2096
Δx/m 0 0.0342 0.0389 0.0418 0.0453 0.0494
Δt/s 0 0.06 0.06 0.06 0.06 0.06
v/(m·s-1) 0.57 0.65 0.70 0.76 0.82
(2)由图像的纵、横坐标可知任一时刻速度的大小和方向或物体的某一速度所对应的时刻。
认识图像:
(4)匀速直线运动的速度图象是一条平行于时间轴的直线.
(3)v-t图像只能描述直线运动的情况,在v-t图像中速度只有正负两个方向。
(1)图线上的“点”表示物体所处的状态,“图线”表示速度随时间的变化规律。它并不表示物体运动的轨迹。
平均速度 瞬时速度
物理意义 粗略描述运动快慢,与一段时间或一段位移相对应 精确描述运动快慢,与某一时刻或某一位置相对应
大小 (Δt极小)
方向 与位移方向相同,与运动方向不一定相同 与运动方向相同,与位移方向不一定相同
联系 1.瞬时速度为0,平均速度一定为0。平均速度为0,瞬时速度不一定为0。 2.匀速直线运动,平均速度等于瞬时速度。 3.当位移足够小或Δt足够短时可以认为平均速度等于瞬时速度。
“平均速度”与“瞬时速度”的区别
通过每段的初、末速度大小比较看出。
OA段加速,AB段匀速,BC段加速,CD段减速,DE段反向加速。
12
5
-12
5
14
18
22
t/s
v/(m·s-1)
A
B
C
D
E
问题:
例5、 (多选)若一质点从t=0开始由原点出发,其v-t图象如图所示,则该质点( )
A.当t=1 s时,离原点最远
B.当t=2 s时,离原点最远
C.当t=3 s时,回到原点
D.当t=4 s时,回到原点
BD
若为x-t图像?
