湘教版数学八年级下册1.2直角三角形的性质和判定(2) 课件(共13张PPT)
文档属性
| 名称 | 湘教版数学八年级下册1.2直角三角形的性质和判定(2) 课件(共13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-09 17:15:30 | ||
图片预览





文档简介
(共13张PPT)
直角三角形的性质和判定1(2)
第一章
1、直角三角形有哪些性质?
新课引入
2.直角三角形的判定定理有哪些?
直角三角形的两个锐角互余.
直角三角形斜边上的中线等于斜边的一半.
有两个角互余的三角形是直角三角形.
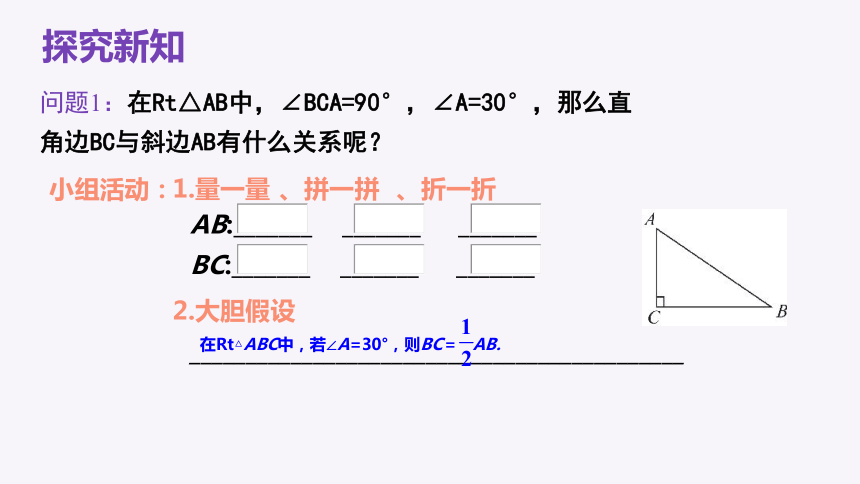
问题1:在Rt△AB中,∠BCA=90°,∠A=30°,那么直角边BC与斜边AB有什么关系呢?
探究新知
小组活动:
1.量一量
AB:_______ _______ _______
BC:_______ _______ _______
2.大胆假设
____________________________________________
在Rt△ABC中,若∠A=30°,则BC= AB.
、拼一拼
、折一折
证明:如图1-6,取线段AB的中点D,连接CD.
∵CD是Rt△ABC斜边AB上的中线,
∴CD=AB=BD.
∵∠BCA=90°,且∠A =30°,
∴∠B=60°.
∴△CBD为等边三角形,
∴BC=BD=AB.
如图1-6,在Rt△ABC中,∠BCA=90°,如果∠A=30°,那么直角边BC与斜边AB有什么关系呢
探究新知
C
B
A
图1-6
30°
D
总结归纳
在直角三角形中,如果一个锐角等于30°,那么这个直角所对的边等于斜边的一半.
几何语言:
∵ 在 Rt△ABC 中,∠C = 90°,∠A = 30°,
∴ BC = AB.
C
B
A
图1-6
30°
随堂跟练
(1)直角三角形中 30° 角所对的直角边等于另一直角边的一半.
(2)三角形中 30° 角所对的边等于最长边的一半.
(3)直角三角形中最小的直角边是斜边的一半.
1.判断
2.如图,在 Rt△ABC 中,∠ACB=90°,∠B=30°,CD 是斜边 AB 上的高,AD=3 cm,则 AB 的长度是( )
A.3 cm B.6 cm
C.9 cm D.12 cm
D
问题2 如图,在 Rt△ABC 中,如果 BC = AB,那么 ∠A 等于多少?
探究新知
解:如图,取线段 AB 的中点 D,连接 CD.
∵CD 是 Rt△ABC 斜边 AB 上的中线,
∴CD = AB = BD = BC,
即△BDC 为等边三角形.
∴∠B = 60°.
∵∠B +∠A = 90°,
∴∠A = 30°.
B
C
A
D
总结归纳
在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于 30°.
几何语言:
∵ 在 Rt△ABC 中,∠C = 90°,
BC = AB
∴∠A = 30°.
探究新知
例3 如图1-8,在A岛周围20海里水域内有暗礁,一轮船由西向东航行到O处时,测得A岛在北偏东60°的方向,且与轮船相距 海里.若该船继续保持由西向东的航向,那么有触礁的危险吗
D
当堂练习
1.如图,在△ABC中,∠C=45°,∠BAC=105°,AD⊥BC,DC=5cm,则AB=( )
A.5cm B.10cm C.15cm D.20cm
B
2. 如图,一棵树在一次强台风中,于离地面 3 米处折断倒下,倒下部分与地面成 30° 角,这棵树在折断前的高度为( )
A.6 米 B.9 米
C.12 米 D.15 米
B
3.如果等腰三角形腰长为4,腰上的高为2,则此等腰三角形的顶角度数为________.
60°
4.如图,Rt△ABC 中,∠A = 30°,AB + BC = 12 cm,则AB =______cm.
A
C
B
当堂练习
8
当堂练习
5. 如图所示,在四边形 ACBD 中,AD∥BC,AB⊥AC,且 AC = BC,求∠DAC 的度数.
解:∵AB⊥AC,
∴∠CAB = 90°.
∵AC = BC,
∴∠CBA = 30°.
∵AD∥BC,
∴∠BAD =∠CBA =30°.
∴∠DAC =∠CAB+∠BAD = 120°.
课堂小结
在直角三角形中,如果一个锐角等于 30°,那么它所对的直角边等于斜边的一半
含 30°角的直角三角形的性质
注意
前提条件:含30° 角的直角三角形中
性质
判定
在直角三角形中,如果一条直角边等于斜
边的一半,那么这条直角边所对的角等于 30°.
直角三角形的性质和判定1(2)
第一章
1、直角三角形有哪些性质?
新课引入
2.直角三角形的判定定理有哪些?
直角三角形的两个锐角互余.
直角三角形斜边上的中线等于斜边的一半.
有两个角互余的三角形是直角三角形.
问题1:在Rt△AB中,∠BCA=90°,∠A=30°,那么直角边BC与斜边AB有什么关系呢?
探究新知
小组活动:
1.量一量
AB:_______ _______ _______
BC:_______ _______ _______
2.大胆假设
____________________________________________
在Rt△ABC中,若∠A=30°,则BC= AB.
、拼一拼
、折一折
证明:如图1-6,取线段AB的中点D,连接CD.
∵CD是Rt△ABC斜边AB上的中线,
∴CD=AB=BD.
∵∠BCA=90°,且∠A =30°,
∴∠B=60°.
∴△CBD为等边三角形,
∴BC=BD=AB.
如图1-6,在Rt△ABC中,∠BCA=90°,如果∠A=30°,那么直角边BC与斜边AB有什么关系呢
探究新知
C
B
A
图1-6
30°
D
总结归纳
在直角三角形中,如果一个锐角等于30°,那么这个直角所对的边等于斜边的一半.
几何语言:
∵ 在 Rt△ABC 中,∠C = 90°,∠A = 30°,
∴ BC = AB.
C
B
A
图1-6
30°
随堂跟练
(1)直角三角形中 30° 角所对的直角边等于另一直角边的一半.
(2)三角形中 30° 角所对的边等于最长边的一半.
(3)直角三角形中最小的直角边是斜边的一半.
1.判断
2.如图,在 Rt△ABC 中,∠ACB=90°,∠B=30°,CD 是斜边 AB 上的高,AD=3 cm,则 AB 的长度是( )
A.3 cm B.6 cm
C.9 cm D.12 cm
D
问题2 如图,在 Rt△ABC 中,如果 BC = AB,那么 ∠A 等于多少?
探究新知
解:如图,取线段 AB 的中点 D,连接 CD.
∵CD 是 Rt△ABC 斜边 AB 上的中线,
∴CD = AB = BD = BC,
即△BDC 为等边三角形.
∴∠B = 60°.
∵∠B +∠A = 90°,
∴∠A = 30°.
B
C
A
D
总结归纳
在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的角等于 30°.
几何语言:
∵ 在 Rt△ABC 中,∠C = 90°,
BC = AB
∴∠A = 30°.
探究新知
例3 如图1-8,在A岛周围20海里水域内有暗礁,一轮船由西向东航行到O处时,测得A岛在北偏东60°的方向,且与轮船相距 海里.若该船继续保持由西向东的航向,那么有触礁的危险吗
D
当堂练习
1.如图,在△ABC中,∠C=45°,∠BAC=105°,AD⊥BC,DC=5cm,则AB=( )
A.5cm B.10cm C.15cm D.20cm
B
2. 如图,一棵树在一次强台风中,于离地面 3 米处折断倒下,倒下部分与地面成 30° 角,这棵树在折断前的高度为( )
A.6 米 B.9 米
C.12 米 D.15 米
B
3.如果等腰三角形腰长为4,腰上的高为2,则此等腰三角形的顶角度数为________.
60°
4.如图,Rt△ABC 中,∠A = 30°,AB + BC = 12 cm,则AB =______cm.
A
C
B
当堂练习
8
当堂练习
5. 如图所示,在四边形 ACBD 中,AD∥BC,AB⊥AC,且 AC = BC,求∠DAC 的度数.
解:∵AB⊥AC,
∴∠CAB = 90°.
∵AC = BC,
∴∠CBA = 30°.
∵AD∥BC,
∴∠BAD =∠CBA =30°.
∴∠DAC =∠CAB+∠BAD = 120°.
课堂小结
在直角三角形中,如果一个锐角等于 30°,那么它所对的直角边等于斜边的一半
含 30°角的直角三角形的性质
注意
前提条件:含30° 角的直角三角形中
性质
判定
在直角三角形中,如果一条直角边等于斜
边的一半,那么这条直角边所对的角等于 30°.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
