2.3.1等腰(边)三角形的性质 课件(共21张PPT)湘教版数学八年级上册
文档属性
| 名称 | 2.3.1等腰(边)三角形的性质 课件(共21张PPT)湘教版数学八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-09 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
2.3 等腰三角形
第2章 三角形
第1课时 等腰(边)三角形的性质
等腰三角形
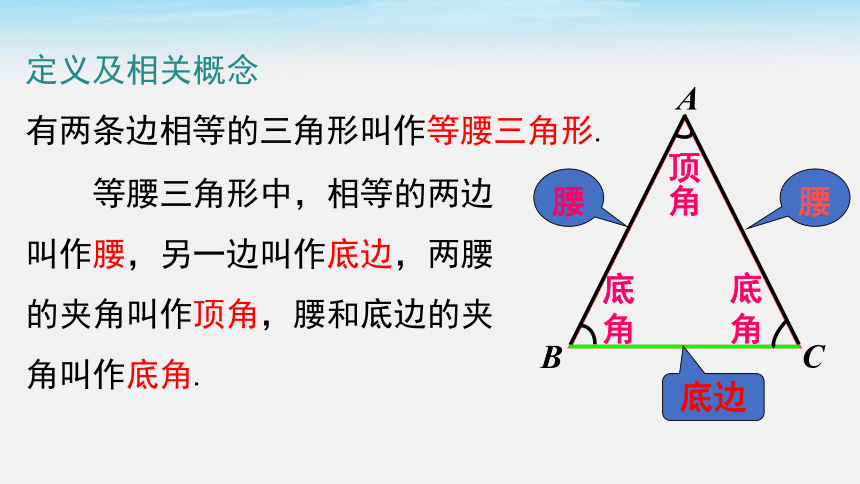
定义及相关概念
有两条边相等的三角形叫作等腰三角形.
等腰三角形中,相等的两边叫作腰,另一边叫作底边,两腰的夹角叫作顶角,腰和底边的夹角叫作底角.
A
C
B
腰
腰
底边
顶角
底角
底角
剪一剪:把一张长方形的纸按图中的红线对折,并剪下蓝色部分(一个直角三角形),再把得到的直角三角形展开,得到的三角形有什么特点?
互动探究
等腰三角形的性质
A
B
C
AB = AC
等腰三角形
操作内容:
1、按照步骤,用剪刀裁剪一个等腰三角形。
2、这个三角形是轴对称图形吗?它的对称轴是什么?
操作时间:3分钟
3分钟
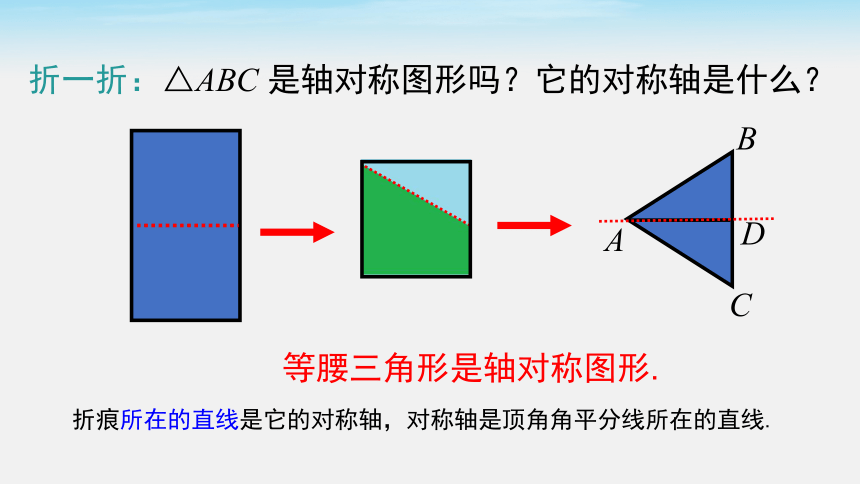
折一折:△ABC 是轴对称图形吗?它的对称轴是什么?
A
C
D
B
折痕所在的直线是它的对称轴,对称轴是顶角角平分线所在的直线.
等腰三角形是轴对称图形.
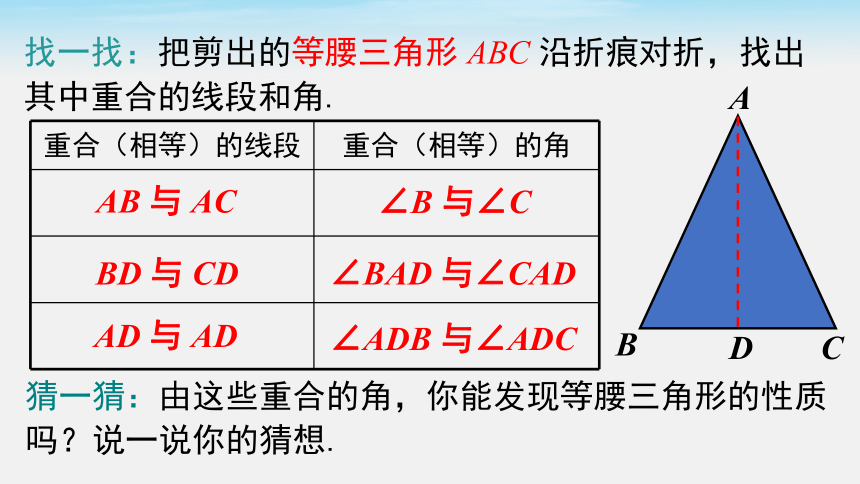
找一找:把剪出的等腰三角形 ABC 沿折痕对折,找出其中重合的线段和角.
重合(相等)的线段 重合(相等)的角
A
C
B
D
AB 与 AC
BD 与 CD
AD 与 AD
∠B 与∠C
∠BAD 与∠CAD
∠ADB 与∠ADC
猜一猜:由这些重合的角,你能发现等腰三角形的性质吗?说一说你的猜想.
由此得到等腰三角形的性质定理:
等腰三角形是轴对称图形,对称轴是顶角平分线所在的直线.
等腰三角形的两底角相等(简称“等边对等角”).
总结归纳
等腰三角形底边上的高、中线及顶角平分线重合(简称“三线合一”).
画出任意一个等腰三角形的底角平分线、这个底角所对的腰上的中线和高,看看它们是否重合?
不重合!
三线合一
为什么不一样
1. 等腰三角形的顶角一定是锐角.
2. 等腰三角形的底角可能是锐角或者直角、钝角.
3. 等腰三角形的角平分线、中线和高互相重合.
4. 等腰三角形底边上的中线一定平分顶角.
( X )
( X )
( X )
(√)
明辨是非
判断下列说法正误:
A
B
C
D
(
(
1
2
填一填:根据等腰三角形的性质定理完成下列填空.
在△ABC 中,AB = AC.
(1) ∵ AD⊥BC,
∴∠____=∠____,_____=_____.
(2) ∵ BD=CD,
∴ ____⊥____,∠____ =∠____.
(3) ∵ ∠1=∠2,
∴ ____⊥____,____ =____.
1
2
2
BD
CD
AD
BC
BD
1
BC
AD
CD
例 已知:如图,在△ABC 中,AB = AC,点 D,E 在边 BC 上,且 AD = AE. 求证:BD = CE.
证明:作 AF⊥BC,垂足为点 F,
则 AF 是等腰△ABC 和等腰△ADE 底边上的高,也是底边上的中线.
∴ BF = CF,
∴ BF - DF = CF - EF,
DF = EF.
即 BD = CE.
F
典例精析
方法总结:在等腰三角形的有关计算或证明中,会遇到一些添加辅助线的问题,其顶角平分线、底边上的高、底边上的中线是常见的辅助线.
问题1 等边三角形的三个内角之间有什么关系?
A
B
C
A
B
C
等腰三角形
AB = AC
∠B = ∠C
等边三角形
AB = AC = BC
AB = AC
∠B =∠C
AC = BC
∠A =∠B
∠A =∠B =∠C
类比探究
等边三角形的性质
性质:等边三角形的三个内角相等,且都等于 60°.
已知:△ABC 中,AB = AC = BC.
求证:∠A =∠B =∠C = 60°.
证明: ∵ AB = AC,
∴∠B =∠C (等边对等角).
同理,∠A =∠C.
∴∠A =∠B =∠C.
∵∠A +∠B +∠C = 180°,
∴∠A =∠B =∠C = 60°.
A
B
C
A
B
C
A
B
C
问题 等边三角形有“三线合一”的性质吗?等边三角形有几条对称轴?
结论:等边三角形每条边上的中线,高和所对角的平分线都“三线合一”.
顶角的平分线、底边的高
底边的中线
三线合一
一条对称轴
三条对称轴
2. 如图,在△ABC 中,AB = AC,过点 A 作 AD∥BC,若∠1 = 70°,则∠BAC 的大小为( )
A.30° B.40° C.50° D.70°
B
1. 等腰三角形有一个角是 90°,则另两个角的度数分别是 ( )
A. 30°,60° B. 45°,45°
C. 45°,90° D. 20°,70°
B
A
B
C
D
1
⌒
3. (1) 等腰三角形一个底角为 75°,它的另外两个角为
__________;
(2) 等腰三角形的一个角为 36°,它的另外两个角为
____________________;
(3) 等腰三角形的一个角为 120°,它的另外两个角为
.
75°,30°
72°,72° 或 36°,108°
30°,30°
4. 如图,在△ABC 中,AB = AC,D 是 BC 边上的中点,
∠B = 30°,求∠BAD 和 ∠ADC 的度数.
A
B
C
D
解:∵ AB = AC,D 是 BC 边上的中点,
∴∠C =∠B = 30°,
∠ADC = 90°.
∴∠BAD =∠ADC -∠B = 90° - 30° = 60°.
5. 如图,点 P 为等边△ABC 的边 BC 上一点,且∠APD = 80°,AD = AP,求∠DPC 的度数.
解:∵△ABC 是等边三角形,
∴∠C = 60°.
∵ AD = AP,
∴∠APD =∠ADP = 80°.
∴∠DPC =∠ADP -∠C = 20°.
等腰三角形的性质
等边对等角
三线合一
注意是指同一个三角形中
注意是指顶角的平分线,底边上的高和中线才有这一性质.而腰上高和中线与底角的平分线不具有这一性质.
推论
等边三角形三个内角相等,且均等于 60°
2.3 等腰三角形
第2章 三角形
第1课时 等腰(边)三角形的性质
等腰三角形
定义及相关概念
有两条边相等的三角形叫作等腰三角形.
等腰三角形中,相等的两边叫作腰,另一边叫作底边,两腰的夹角叫作顶角,腰和底边的夹角叫作底角.
A
C
B
腰
腰
底边
顶角
底角
底角
剪一剪:把一张长方形的纸按图中的红线对折,并剪下蓝色部分(一个直角三角形),再把得到的直角三角形展开,得到的三角形有什么特点?
互动探究
等腰三角形的性质
A
B
C
AB = AC
等腰三角形
操作内容:
1、按照步骤,用剪刀裁剪一个等腰三角形。
2、这个三角形是轴对称图形吗?它的对称轴是什么?
操作时间:3分钟
3分钟
折一折:△ABC 是轴对称图形吗?它的对称轴是什么?
A
C
D
B
折痕所在的直线是它的对称轴,对称轴是顶角角平分线所在的直线.
等腰三角形是轴对称图形.
找一找:把剪出的等腰三角形 ABC 沿折痕对折,找出其中重合的线段和角.
重合(相等)的线段 重合(相等)的角
A
C
B
D
AB 与 AC
BD 与 CD
AD 与 AD
∠B 与∠C
∠BAD 与∠CAD
∠ADB 与∠ADC
猜一猜:由这些重合的角,你能发现等腰三角形的性质吗?说一说你的猜想.
由此得到等腰三角形的性质定理:
等腰三角形是轴对称图形,对称轴是顶角平分线所在的直线.
等腰三角形的两底角相等(简称“等边对等角”).
总结归纳
等腰三角形底边上的高、中线及顶角平分线重合(简称“三线合一”).
画出任意一个等腰三角形的底角平分线、这个底角所对的腰上的中线和高,看看它们是否重合?
不重合!
三线合一
为什么不一样
1. 等腰三角形的顶角一定是锐角.
2. 等腰三角形的底角可能是锐角或者直角、钝角.
3. 等腰三角形的角平分线、中线和高互相重合.
4. 等腰三角形底边上的中线一定平分顶角.
( X )
( X )
( X )
(√)
明辨是非
判断下列说法正误:
A
B
C
D
(
(
1
2
填一填:根据等腰三角形的性质定理完成下列填空.
在△ABC 中,AB = AC.
(1) ∵ AD⊥BC,
∴∠____=∠____,_____=_____.
(2) ∵ BD=CD,
∴ ____⊥____,∠____ =∠____.
(3) ∵ ∠1=∠2,
∴ ____⊥____,____ =____.
1
2
2
BD
CD
AD
BC
BD
1
BC
AD
CD
例 已知:如图,在△ABC 中,AB = AC,点 D,E 在边 BC 上,且 AD = AE. 求证:BD = CE.
证明:作 AF⊥BC,垂足为点 F,
则 AF 是等腰△ABC 和等腰△ADE 底边上的高,也是底边上的中线.
∴ BF = CF,
∴ BF - DF = CF - EF,
DF = EF.
即 BD = CE.
F
典例精析
方法总结:在等腰三角形的有关计算或证明中,会遇到一些添加辅助线的问题,其顶角平分线、底边上的高、底边上的中线是常见的辅助线.
问题1 等边三角形的三个内角之间有什么关系?
A
B
C
A
B
C
等腰三角形
AB = AC
∠B = ∠C
等边三角形
AB = AC = BC
AB = AC
∠B =∠C
AC = BC
∠A =∠B
∠A =∠B =∠C
类比探究
等边三角形的性质
性质:等边三角形的三个内角相等,且都等于 60°.
已知:△ABC 中,AB = AC = BC.
求证:∠A =∠B =∠C = 60°.
证明: ∵ AB = AC,
∴∠B =∠C (等边对等角).
同理,∠A =∠C.
∴∠A =∠B =∠C.
∵∠A +∠B +∠C = 180°,
∴∠A =∠B =∠C = 60°.
A
B
C
A
B
C
A
B
C
问题 等边三角形有“三线合一”的性质吗?等边三角形有几条对称轴?
结论:等边三角形每条边上的中线,高和所对角的平分线都“三线合一”.
顶角的平分线、底边的高
底边的中线
三线合一
一条对称轴
三条对称轴
2. 如图,在△ABC 中,AB = AC,过点 A 作 AD∥BC,若∠1 = 70°,则∠BAC 的大小为( )
A.30° B.40° C.50° D.70°
B
1. 等腰三角形有一个角是 90°,则另两个角的度数分别是 ( )
A. 30°,60° B. 45°,45°
C. 45°,90° D. 20°,70°
B
A
B
C
D
1
⌒
3. (1) 等腰三角形一个底角为 75°,它的另外两个角为
__________;
(2) 等腰三角形的一个角为 36°,它的另外两个角为
____________________;
(3) 等腰三角形的一个角为 120°,它的另外两个角为
.
75°,30°
72°,72° 或 36°,108°
30°,30°
4. 如图,在△ABC 中,AB = AC,D 是 BC 边上的中点,
∠B = 30°,求∠BAD 和 ∠ADC 的度数.
A
B
C
D
解:∵ AB = AC,D 是 BC 边上的中点,
∴∠C =∠B = 30°,
∠ADC = 90°.
∴∠BAD =∠ADC -∠B = 90° - 30° = 60°.
5. 如图,点 P 为等边△ABC 的边 BC 上一点,且∠APD = 80°,AD = AP,求∠DPC 的度数.
解:∵△ABC 是等边三角形,
∴∠C = 60°.
∵ AD = AP,
∴∠APD =∠ADP = 80°.
∴∠DPC =∠ADP -∠C = 20°.
等腰三角形的性质
等边对等角
三线合一
注意是指同一个三角形中
注意是指顶角的平分线,底边上的高和中线才有这一性质.而腰上高和中线与底角的平分线不具有这一性质.
推论
等边三角形三个内角相等,且均等于 60°
同课章节目录
