北师大版数学七年级下册课件1.2 幂的乘方与积的乘方(共19张PPT)
文档属性
| 名称 | 北师大版数学七年级下册课件1.2 幂的乘方与积的乘方(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 549.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-26 20:51:32 | ||
图片预览






文档简介
课件19张PPT。第2课时 幂的乘方与积的乘方1.根据乘方的意义填空:
a·a·a= a2 a2 a2= ___________
am am am= (m为正整数)
2.若已知一个正方体的棱长为1.1×103cm,你能计算出它的体积是多少吗?
3.你能说出444与533 两个数中,哪个比较大吗?
学习本节后你就可以回答这个问题了! 创设情景 明确目标1.理解幂的乘方法则;
2.运用幂的乘方法则进行计算;
3. 理解积的乘方法则;
4.运用积的乘方法则进行计算.
学习目标探究点一 幂的乘方法则的推导 根据乘方的意义及同底数幂的乘法填空,看看计算的结果有什么规律:
(1)(32)3 = 32×32×32 = 3( )
(2)(a2)3 = a2 × a2 × a2 =a( )
(3)(am)3 = = (m是正整数)对于任意底数a与任意正整数m、n,(am)n =am.am… …am
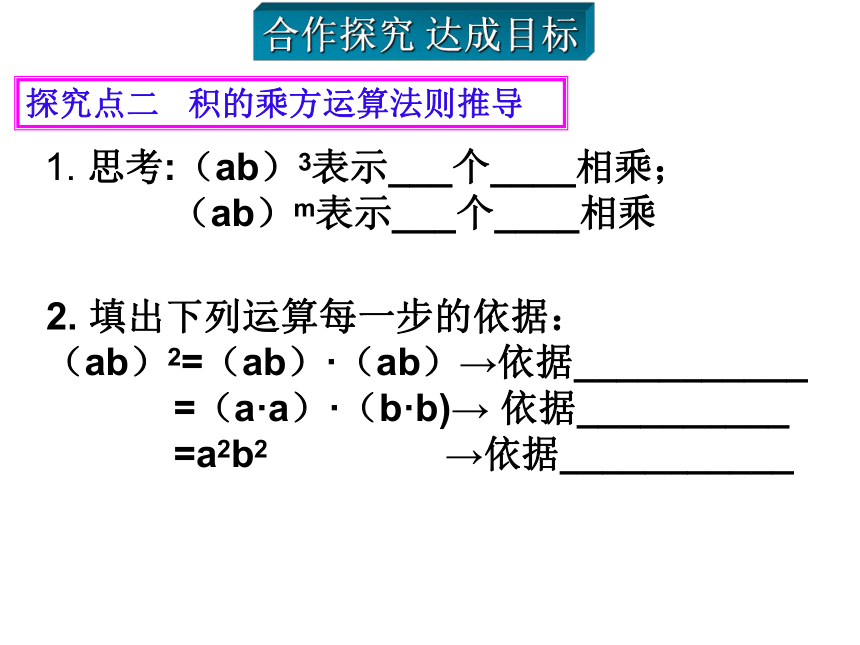
=am+m+…+m=amn(乘方的意义)(同底数幂相乘)合作探究 达成目标幂的乘方运算法则(m,n都是正整数)幂的乘方,底数________,指数_______.不变相乘幂的乘方法则一定要与同底数幂相乘的乘法法则区分开:两个法则都是底数不变,但同底数幂相乘时,指数相加;而幂的乘方时,指数相乘,这是本质区别.点拨升华探究点二 积的乘方运算法则推导 1. 思考:(ab)3表示___个____相乘;
(ab)m表示___个____相乘 2. 填出下列运算每一步的依据:
(ab)2=(ab)·(ab)→依据___________
=(a·a)·(b·b)→ 依据__________
=a2b2 →依据___________合作探究 达成目标 (ab)3 (ab)4 = (ab)? (ab)?(ab) = (a?a?a)?(b?b?b) = a3b3= a4b4试一试计算:你能说明你的猜想的正确性吗?由 (ab)3 = a3b3 (ab)4 = a4b4 anbn从左到右的变化 你能发现有何运算规律吗? 积的乘方: 根据乘方的意义和乘法的运算律,计算:
(n是正整数).(n是正整数). 当n 是正整数时,三个或三个以上因式的积的乘
方,也具有这一性质吗? 归纳 积的乘方,等于把积的每一个因式分别乘方,再
把所得的幂相乘.推广: 能用文字语言概述你发现的积的乘方运算规律吗?思考: 如何区分同底数幂相乘,幂的乘方,积的乘方这三个运算法则? 一是注意运算形式:同底数幂相乘是______运算,幂的乘方是______运算;二是注意法则,即(幂的)乘法指数就是____, (幂的)乘方指数就是____;积的乘方就是先将各个因式先_____再相_____.点拨升华探究点三 幂的乘方与积的乘方的应用 对于幂的运算,应当先观察形式:是同底数幂的乘法,还是幂的乘方,再应用相应的法则进行运算 .在幂的运算中若混合应用多个幂的运算法则时,应当先算_____,再算_____,最后再按四则混合运算顺序依次运算.
点拨升华 练习 计算下列各题:
(1) (2)
(3) (4)
(5) (6) 解:因为 ,
又 25=52,
所以 ,
故 . 例2 已知: ,求 的值. 解: ∵
∴
即 例3 若 比较a、b、c 的大小.乘方的
意义幂的乘方法则1.知识结构图 2.理解积的乘方法则,并能灵活进行运算;3.正确区分同底数幂、幂的乘方、积的乘方运算法则,并能灵活运用. 同底数幂的乘法法则积的乘方法则计算
实际
运用总结梳理 内化目标 1.(a2)3 = ;(x6)5 = _____
2.(am)4 = ; (x3m)2n =______
3.若a2m = 4,则a3m =_______
达标检测 反思目标6.计算:
(1)(ym)2·(- y3) (2)(y2)3·y2 + (y2)2 y4
1.上交作业:
一.计算
(1)- b·(- b3)5 (2)2(x3)5 - (x5)3 (3)a·(a2)4·(- a2)
二. 已知am = 2 , bm= 5 ,求(a3)m +(b2)m的值。
祝同学们学习愉快!
a·a·a= a2 a2 a2= ___________
am am am= (m为正整数)
2.若已知一个正方体的棱长为1.1×103cm,你能计算出它的体积是多少吗?
3.你能说出444与533 两个数中,哪个比较大吗?
学习本节后你就可以回答这个问题了! 创设情景 明确目标1.理解幂的乘方法则;
2.运用幂的乘方法则进行计算;
3. 理解积的乘方法则;
4.运用积的乘方法则进行计算.
学习目标探究点一 幂的乘方法则的推导 根据乘方的意义及同底数幂的乘法填空,看看计算的结果有什么规律:
(1)(32)3 = 32×32×32 = 3( )
(2)(a2)3 = a2 × a2 × a2 =a( )
(3)(am)3 = = (m是正整数)对于任意底数a与任意正整数m、n,(am)n =am.am… …am
=am+m+…+m=amn(乘方的意义)(同底数幂相乘)合作探究 达成目标幂的乘方运算法则(m,n都是正整数)幂的乘方,底数________,指数_______.不变相乘幂的乘方法则一定要与同底数幂相乘的乘法法则区分开:两个法则都是底数不变,但同底数幂相乘时,指数相加;而幂的乘方时,指数相乘,这是本质区别.点拨升华探究点二 积的乘方运算法则推导 1. 思考:(ab)3表示___个____相乘;
(ab)m表示___个____相乘 2. 填出下列运算每一步的依据:
(ab)2=(ab)·(ab)→依据___________
=(a·a)·(b·b)→ 依据__________
=a2b2 →依据___________合作探究 达成目标 (ab)3 (ab)4 = (ab)? (ab)?(ab) = (a?a?a)?(b?b?b) = a3b3= a4b4试一试计算:你能说明你的猜想的正确性吗?由 (ab)3 = a3b3 (ab)4 = a4b4 anbn从左到右的变化 你能发现有何运算规律吗? 积的乘方: 根据乘方的意义和乘法的运算律,计算:
(n是正整数).(n是正整数). 当n 是正整数时,三个或三个以上因式的积的乘
方,也具有这一性质吗? 归纳 积的乘方,等于把积的每一个因式分别乘方,再
把所得的幂相乘.推广: 能用文字语言概述你发现的积的乘方运算规律吗?思考: 如何区分同底数幂相乘,幂的乘方,积的乘方这三个运算法则? 一是注意运算形式:同底数幂相乘是______运算,幂的乘方是______运算;二是注意法则,即(幂的)乘法指数就是____, (幂的)乘方指数就是____;积的乘方就是先将各个因式先_____再相_____.点拨升华探究点三 幂的乘方与积的乘方的应用 对于幂的运算,应当先观察形式:是同底数幂的乘法,还是幂的乘方,再应用相应的法则进行运算 .在幂的运算中若混合应用多个幂的运算法则时,应当先算_____,再算_____,最后再按四则混合运算顺序依次运算.
点拨升华 练习 计算下列各题:
(1) (2)
(3) (4)
(5) (6) 解:因为 ,
又 25=52,
所以 ,
故 . 例2 已知: ,求 的值. 解: ∵
∴
即 例3 若 比较a、b、c 的大小.乘方的
意义幂的乘方法则1.知识结构图 2.理解积的乘方法则,并能灵活进行运算;3.正确区分同底数幂、幂的乘方、积的乘方运算法则,并能灵活运用. 同底数幂的乘法法则积的乘方法则计算
实际
运用总结梳理 内化目标 1.(a2)3 = ;(x6)5 = _____
2.(am)4 = ; (x3m)2n =______
3.若a2m = 4,则a3m =_______
达标检测 反思目标6.计算:
(1)(ym)2·(- y3) (2)(y2)3·y2 + (y2)2 y4
1.上交作业:
一.计算
(1)- b·(- b3)5 (2)2(x3)5 - (x5)3 (3)a·(a2)4·(- a2)
二. 已知am = 2 , bm= 5 ,求(a3)m +(b2)m的值。
祝同学们学习愉快!
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
