选择必修 第一章 1.4.1用空间向量研究直线、平面位置关系 3空间中直线、平面的垂直(25页ppt)
文档属性
| 名称 | 选择必修 第一章 1.4.1用空间向量研究直线、平面位置关系 3空间中直线、平面的垂直(25页ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-09-18 10:34:49 | ||
图片预览








文档简介
(共25张PPT)
选择必修 第一章
1.4.1 用空间向量研究直线、平面的位置关系
3.空间中直线、平面的垂直
人教A版(2019)
教学目标
学习目标 数学素养
1.能用向量语言表述直线与直线、直线与平面、平面与平面的垂直关系. 1.数学抽象素养和空间直观素养.
2.掌握利用向量方法证明直线与平面、平面与平面垂直. 2.空间直观素养和逻辑推理素养.
温故知新
1.设分别是直线l1,l2的方向向量.则
2.设是直线l的方向向量,是平面α的法向量,l α,则
l1∥l2 ∥
λ∈R,使得=λ.
x1=λx2,y1=λy2,z1=λz2.
l∥α ⊥ .
=0
x1x2+y1y2+z1z2=0.
3.设、分别是平面α,β的法向量,则
α∥β ∥ .
λ∈R,使得=λ
x1=λx2,y1=λy2,z1=λz2 .
4.空间中的垂直关系有哪些?
直线与直线、直线与平面、平面与平面垂直.
新知探究
类似空间中直线、平面平行的向量表示,在直线与直线、直线与平面、平面与平面的垂直关系中,直线的方向向量、平面的法向量之间有什么关系?
一般地,
直线与直线垂直,就是两直线的方向向量垂直;
直线与平面垂直,就是直线的方向向量与平面的法向量平行;
平面与平面垂直,就是两平面的法向量垂直.
新知探究
如图,设直线l1,l2的方向向量分别是 ,则
1.直线与直线垂直
l1 l2 .
思考:如何用向量的坐标刻画直线与直线垂直关系?
设直线l1,l2的方向向量=(x1,y1,z1), =(x2,y2,z2),则
l1 l2 .
x1x2+y1y2+z1z2=0.
新知探究
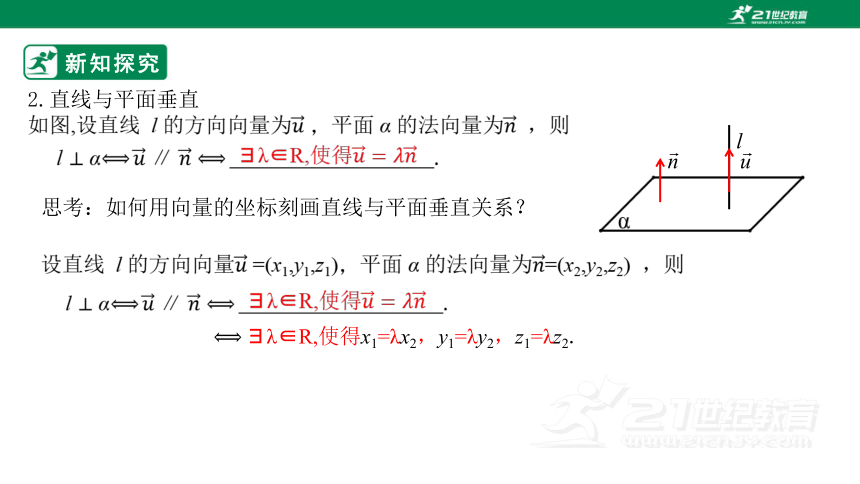
如图,设直线 l 的方向向量为 ,平面 α 的法向量为 ,则
2.直线与平面垂直
l α .
λ∈R,使得
思考:如何用向量的坐标刻画直线与平面垂直关系?
设直线 l 的方向向量 =(x1,y1,z1),平面 α 的法向量为=(x2,y2,z2) ,则
l α .
λ∈R,使得
λ∈R,使得x1=λx2,y1=λy2,z1=λz2.
新知探究
如图,设平面 α ,β的法向量分别为 ,则
3.平面与平面垂直
α β .
思考:如何用向量的坐标刻画平面与平面垂直关系?
设设平面 α ,β的法向量 =(x1,y1,z1),=(x2,y2,z2) ,则
α β .
x1x2+y1y2+z1z2=0.
我们随时随地向量运算的作用,你同意“向量是躯体,运算是灵魂”“没有运算的向量只起路标的作用”的说法吗?
新知探究
【例1】如图,已知正三棱柱ABC-A1B1C1的各棱长都是1,M是BC的中点,N是侧棱 CC1上的点,且CN=CC1.求证:AB1⊥MN.
证明:
设AB的中点为O,作OO1∥AA1,以O为原点,分别OB,
OC,OO1为x轴,y轴,z轴建立如图空间直角坐标系.则
A(,0,0),B(,0,0),C(0,,0),N(0,,),B1(,0,1),
∵M是BC的中点,
∴=0,
∴=(1,0,1),=(,,),
∴M(,,0)
∴,即AB1⊥MN.
新知探究
【例2】如图,在平行六面体ABCD-A1B1C1D1中,AB=AD=AA1=1,∠A1AB=∠A1AD=∠BAD=60°,求证:直线A1C⊥平面BDD1B1.
证明:
设,,,则{}为空间的一个基底,且,,,
∴,.
分析:根据条件,可以{ }为基底,并用基向量表示和平面BDD1B1,再通过向量运算证明是平面BDD1B1的法向量即可.
∵AB=AD=AA1=1,∠A1AB=∠A1AD=∠BAD=60°,
在平面BDD1B1上,取为基向量,则对于平面BDD1B1上任意一点P,存在唯一的有序实数对(λ,μ),使得,
新知探究
【例2】如图,在平行六面体ABCD-A1B1C1D1中,AB=AD=AA1=1,∠A1AB=∠A1AD=∠BAD=60°,求证:直线A1C⊥平面BDD1B1.
证明:
∴
∴是平面BDD1B1的法向量.
在平面BDD1B1上,取为基向量,则对于平面BDD1B1上任意一点P,存在唯一的有序实数对(λ,μ),使得,
==0,
∴直线A1C⊥平面BDD1B1.
新知探究
【例3】证明“平面与平面垂直的判定定理”:若一个平面过另一个平面的垂线,则这两个平面垂直.
证明:
取直线l的方向向量,平面β的法向量为,因为l⊥α,所以是平面α的法向量.
∴,
∵l β,而平面β的法向量,
已知:如图,l⊥α,l β,求证:α⊥β.
∴α⊥β.
新知探究
【例4】如图,在正方体ABCD-A1B1C1D1中,O是AC与BD的交点,G是CC1的中点.
求证:A1O⊥平面GBD.
证明:
方法1:设正方体棱长为2,以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示空间直角坐标系.则
∴,
∴,,
∴,即OA1⊥DB,OA1⊥BG,
D(0,0,0),O(1,1,0),A1(2,0,2),B(2,2,0),G(0,2,1),
∴OA1⊥平面GBD.
又DB∩BG=B,
新知探究
【例4】如图,在正方体ABCD-A1B1C1D1中,O是AC与BD的交点,G是CC1的中点.
求证:A1O⊥平面GBD.
证明:
方法2:同方法1建立空间直角坐标系,可得
,
设平面GBD的法向量=(x,y,z),则
令x=1,则y=-1,z=2,
∴OA1⊥平面GBD.
即,
,即,
∴平面GBD的一个法向量为=(1,-1,2)
新知探究
利用坐标法证明线面垂直的方法
(1)基向量法:选取基向量,用基向量表示直线所在的向量,在平面内找出两个不共线的向量,也用基向量表示,然后根据数量积运算律分别证明直线所在向量与两个不共线向量的数量积均为零,从而证得结论.
(2)坐标法:建立空间直角坐标系,求出直线方向向量的坐标以及平面内两个不共线向量的坐标,然后根据数量积的坐标运算法则证明直线的方向向量与两个不共线向量的数量积均为零,从而证得结论.
(3)法向量法:建立空间直角坐标系,求出直线方向向量的坐标以及平面法向量的坐标,然后说明直线方向向量与平面法向量共线,从而证得结论.
初试身手
1.⑴如图所示,在正方体ABCD-A1B1C1D1中,O是底面正方形ABCD的中心,M是D1D的中点,N是A1B1的中点,则NO,AM直线的位置关系是( )
A.平行 B.相交 C.异面垂直 D.异面不垂直
⑴设正方形的棱长为2,如图所示,建立空间直角坐标系,则
A(2,0,0),M(0,0,1),O(1,1,0),N(2,1,2),
⑵∵平面的法向量为=(1,3,z).又与α平面平行,
∵,
∴=(-2,0,1),=(-1,0,-2),
解得z=3.
⑵已知直线l与平面α垂直,直线l的一个方向向量为=(1,3,z),向量=(3,-2,1)与平面α平行,则z=__________.
解:
x
y
z
∴
∴,即NO⊥AM,故选C.
-3
C
初试身手
2.如图,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠ABC=
∠BCD=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD所成的角为30°.
求证:⑴CM∥平面PAD;
⑵平面PAB⊥平面PAD.
证明:
如图,以点C为坐标原点,分别以CB,CD,CP所在的直线为x轴、y轴、z轴建立的空间直角坐标系C-xyz.
∴PB=4,BC=2,
∵PC=2,
∴=(0,-1,2),=(2,3,0),=(,0,).
∴D(0,1,0),B(2,0,0),A(2,4,0),P(0,0,2),M(,0,),
∵PC⊥平面ABCD,
∴∠PBC为PB与平面ABCD所成的角.即∠PBC=30°.
初试身手
2.如图,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠ABC=
∠BCD=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD所成的角为30°.
求证:⑴CM∥平面PAD;
⑵平面PAB⊥平面PAD.
证明:
⑴设=(x,y,z)为平面PAD的法向量,则
∴CM∥平面PAD.
∵=0,
又CM 平面PAD,
∴,
,即,
令z=1,则y=2,x=-,=(-,2,1),
初试身手
2.如图,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠ABC=
∠BCD=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD所成的角为30°.
求证:⑴CM∥平面PAD;
⑵平面PAB⊥平面PAD.
证明:
⑵如图,取AP的中点为E,连接BE,则
∴BE⊥平面PAD.
∵=0,
又PA∩DA=A,
∴,即BE⊥DA,
E(,2,1),=(-,2,1),
∵PB=AB=4,
∴BE⊥PA,
又BE 平面PAB,
∴平面PAB⊥平面PAD.
初试身手
3.在四面体ABCD中,AB⊥平面BCD,BC=CD,∠BCD=90°,∠ADB=30°,
E、F分别是AC、AD的中点,求证:平面BEF⊥平面ABC.
证明:
设平面ABC的法向量=(x1,y1,z1), 则
=(0,0,-2),=(,0),=(,,1),=(0,,1),
,即,
令x1=1,则y1=-1,=(1,-1,0).
如图所示,以B为原点建立空间直角坐标系.取AB=2,
BD=,则
B(0,0,0),A(0,0,2),D(0,,0),C(,,0),E(,,1),F(0,,1),
初试身手
3.在四面体ABCD中,AB⊥平面BCD,BC=CD,∠BCD=90°,∠ADB=30°,
E、F分别是AC、AD的中点,求证:平面BEF⊥平面ABC.
证明:
设平面BEF的法向量=(x2,y2,z2), 则
,即,
令y2=1,则z2=-,x2=1,=(1,1,-).
∵=0,
∴,
∴平面BEF⊥平面ABC.
课堂小结
1.空间两条直线垂直
2.空间线面垂直
3.空间面面垂直
设直线l1,l2的方向向量=(x1,y1,z1), =(x2,y2,z2),则
l1 l2 .
x1x2+y1y2+z1z2=0.
设直线 l 的方向向量 =(x1,y1,z1),平面 α 的法向量为=(x2,y2,z2) ,则
l α .
λ∈R,使得
λ∈R,使得x1=λx2,y1=λy2,z1=λz2.
设设平面 α ,β的法向量 =(x1,y1,z1),=(x2,y2,z2) ,则
α β .
x1x2+y1y2+z1z2=0.
作业布置
作业: P33 练习 第1,2,3题
P42-43 习题1.4 第5,11题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
选择必修 第一章
1.4.1 用空间向量研究直线、平面的位置关系
3.空间中直线、平面的垂直
人教A版(2019)
教学目标
学习目标 数学素养
1.能用向量语言表述直线与直线、直线与平面、平面与平面的垂直关系. 1.数学抽象素养和空间直观素养.
2.掌握利用向量方法证明直线与平面、平面与平面垂直. 2.空间直观素养和逻辑推理素养.
温故知新
1.设分别是直线l1,l2的方向向量.则
2.设是直线l的方向向量,是平面α的法向量,l α,则
l1∥l2 ∥
λ∈R,使得=λ.
x1=λx2,y1=λy2,z1=λz2.
l∥α ⊥ .
=0
x1x2+y1y2+z1z2=0.
3.设、分别是平面α,β的法向量,则
α∥β ∥ .
λ∈R,使得=λ
x1=λx2,y1=λy2,z1=λz2 .
4.空间中的垂直关系有哪些?
直线与直线、直线与平面、平面与平面垂直.
新知探究
类似空间中直线、平面平行的向量表示,在直线与直线、直线与平面、平面与平面的垂直关系中,直线的方向向量、平面的法向量之间有什么关系?
一般地,
直线与直线垂直,就是两直线的方向向量垂直;
直线与平面垂直,就是直线的方向向量与平面的法向量平行;
平面与平面垂直,就是两平面的法向量垂直.
新知探究
如图,设直线l1,l2的方向向量分别是 ,则
1.直线与直线垂直
l1 l2 .
思考:如何用向量的坐标刻画直线与直线垂直关系?
设直线l1,l2的方向向量=(x1,y1,z1), =(x2,y2,z2),则
l1 l2 .
x1x2+y1y2+z1z2=0.
新知探究
如图,设直线 l 的方向向量为 ,平面 α 的法向量为 ,则
2.直线与平面垂直
l α .
λ∈R,使得
思考:如何用向量的坐标刻画直线与平面垂直关系?
设直线 l 的方向向量 =(x1,y1,z1),平面 α 的法向量为=(x2,y2,z2) ,则
l α .
λ∈R,使得
λ∈R,使得x1=λx2,y1=λy2,z1=λz2.
新知探究
如图,设平面 α ,β的法向量分别为 ,则
3.平面与平面垂直
α β .
思考:如何用向量的坐标刻画平面与平面垂直关系?
设设平面 α ,β的法向量 =(x1,y1,z1),=(x2,y2,z2) ,则
α β .
x1x2+y1y2+z1z2=0.
我们随时随地向量运算的作用,你同意“向量是躯体,运算是灵魂”“没有运算的向量只起路标的作用”的说法吗?
新知探究
【例1】如图,已知正三棱柱ABC-A1B1C1的各棱长都是1,M是BC的中点,N是侧棱 CC1上的点,且CN=CC1.求证:AB1⊥MN.
证明:
设AB的中点为O,作OO1∥AA1,以O为原点,分别OB,
OC,OO1为x轴,y轴,z轴建立如图空间直角坐标系.则
A(,0,0),B(,0,0),C(0,,0),N(0,,),B1(,0,1),
∵M是BC的中点,
∴=0,
∴=(1,0,1),=(,,),
∴M(,,0)
∴,即AB1⊥MN.
新知探究
【例2】如图,在平行六面体ABCD-A1B1C1D1中,AB=AD=AA1=1,∠A1AB=∠A1AD=∠BAD=60°,求证:直线A1C⊥平面BDD1B1.
证明:
设,,,则{}为空间的一个基底,且,,,
∴,.
分析:根据条件,可以{ }为基底,并用基向量表示和平面BDD1B1,再通过向量运算证明是平面BDD1B1的法向量即可.
∵AB=AD=AA1=1,∠A1AB=∠A1AD=∠BAD=60°,
在平面BDD1B1上,取为基向量,则对于平面BDD1B1上任意一点P,存在唯一的有序实数对(λ,μ),使得,
新知探究
【例2】如图,在平行六面体ABCD-A1B1C1D1中,AB=AD=AA1=1,∠A1AB=∠A1AD=∠BAD=60°,求证:直线A1C⊥平面BDD1B1.
证明:
∴
∴是平面BDD1B1的法向量.
在平面BDD1B1上,取为基向量,则对于平面BDD1B1上任意一点P,存在唯一的有序实数对(λ,μ),使得,
==0,
∴直线A1C⊥平面BDD1B1.
新知探究
【例3】证明“平面与平面垂直的判定定理”:若一个平面过另一个平面的垂线,则这两个平面垂直.
证明:
取直线l的方向向量,平面β的法向量为,因为l⊥α,所以是平面α的法向量.
∴,
∵l β,而平面β的法向量,
已知:如图,l⊥α,l β,求证:α⊥β.
∴α⊥β.
新知探究
【例4】如图,在正方体ABCD-A1B1C1D1中,O是AC与BD的交点,G是CC1的中点.
求证:A1O⊥平面GBD.
证明:
方法1:设正方体棱长为2,以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立如图所示空间直角坐标系.则
∴,
∴,,
∴,即OA1⊥DB,OA1⊥BG,
D(0,0,0),O(1,1,0),A1(2,0,2),B(2,2,0),G(0,2,1),
∴OA1⊥平面GBD.
又DB∩BG=B,
新知探究
【例4】如图,在正方体ABCD-A1B1C1D1中,O是AC与BD的交点,G是CC1的中点.
求证:A1O⊥平面GBD.
证明:
方法2:同方法1建立空间直角坐标系,可得
,
设平面GBD的法向量=(x,y,z),则
令x=1,则y=-1,z=2,
∴OA1⊥平面GBD.
即,
,即,
∴平面GBD的一个法向量为=(1,-1,2)
新知探究
利用坐标法证明线面垂直的方法
(1)基向量法:选取基向量,用基向量表示直线所在的向量,在平面内找出两个不共线的向量,也用基向量表示,然后根据数量积运算律分别证明直线所在向量与两个不共线向量的数量积均为零,从而证得结论.
(2)坐标法:建立空间直角坐标系,求出直线方向向量的坐标以及平面内两个不共线向量的坐标,然后根据数量积的坐标运算法则证明直线的方向向量与两个不共线向量的数量积均为零,从而证得结论.
(3)法向量法:建立空间直角坐标系,求出直线方向向量的坐标以及平面法向量的坐标,然后说明直线方向向量与平面法向量共线,从而证得结论.
初试身手
1.⑴如图所示,在正方体ABCD-A1B1C1D1中,O是底面正方形ABCD的中心,M是D1D的中点,N是A1B1的中点,则NO,AM直线的位置关系是( )
A.平行 B.相交 C.异面垂直 D.异面不垂直
⑴设正方形的棱长为2,如图所示,建立空间直角坐标系,则
A(2,0,0),M(0,0,1),O(1,1,0),N(2,1,2),
⑵∵平面的法向量为=(1,3,z).又与α平面平行,
∵,
∴=(-2,0,1),=(-1,0,-2),
解得z=3.
⑵已知直线l与平面α垂直,直线l的一个方向向量为=(1,3,z),向量=(3,-2,1)与平面α平行,则z=__________.
解:
x
y
z
∴
∴,即NO⊥AM,故选C.
-3
C
初试身手
2.如图,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠ABC=
∠BCD=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD所成的角为30°.
求证:⑴CM∥平面PAD;
⑵平面PAB⊥平面PAD.
证明:
如图,以点C为坐标原点,分别以CB,CD,CP所在的直线为x轴、y轴、z轴建立的空间直角坐标系C-xyz.
∴PB=4,BC=2,
∵PC=2,
∴=(0,-1,2),=(2,3,0),=(,0,).
∴D(0,1,0),B(2,0,0),A(2,4,0),P(0,0,2),M(,0,),
∵PC⊥平面ABCD,
∴∠PBC为PB与平面ABCD所成的角.即∠PBC=30°.
初试身手
2.如图,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠ABC=
∠BCD=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD所成的角为30°.
求证:⑴CM∥平面PAD;
⑵平面PAB⊥平面PAD.
证明:
⑴设=(x,y,z)为平面PAD的法向量,则
∴CM∥平面PAD.
∵=0,
又CM 平面PAD,
∴,
,即,
令z=1,则y=2,x=-,=(-,2,1),
初试身手
2.如图,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠ABC=
∠BCD=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD所成的角为30°.
求证:⑴CM∥平面PAD;
⑵平面PAB⊥平面PAD.
证明:
⑵如图,取AP的中点为E,连接BE,则
∴BE⊥平面PAD.
∵=0,
又PA∩DA=A,
∴,即BE⊥DA,
E(,2,1),=(-,2,1),
∵PB=AB=4,
∴BE⊥PA,
又BE 平面PAB,
∴平面PAB⊥平面PAD.
初试身手
3.在四面体ABCD中,AB⊥平面BCD,BC=CD,∠BCD=90°,∠ADB=30°,
E、F分别是AC、AD的中点,求证:平面BEF⊥平面ABC.
证明:
设平面ABC的法向量=(x1,y1,z1), 则
=(0,0,-2),=(,0),=(,,1),=(0,,1),
,即,
令x1=1,则y1=-1,=(1,-1,0).
如图所示,以B为原点建立空间直角坐标系.取AB=2,
BD=,则
B(0,0,0),A(0,0,2),D(0,,0),C(,,0),E(,,1),F(0,,1),
初试身手
3.在四面体ABCD中,AB⊥平面BCD,BC=CD,∠BCD=90°,∠ADB=30°,
E、F分别是AC、AD的中点,求证:平面BEF⊥平面ABC.
证明:
设平面BEF的法向量=(x2,y2,z2), 则
,即,
令y2=1,则z2=-,x2=1,=(1,1,-).
∵=0,
∴,
∴平面BEF⊥平面ABC.
课堂小结
1.空间两条直线垂直
2.空间线面垂直
3.空间面面垂直
设直线l1,l2的方向向量=(x1,y1,z1), =(x2,y2,z2),则
l1 l2 .
x1x2+y1y2+z1z2=0.
设直线 l 的方向向量 =(x1,y1,z1),平面 α 的法向量为=(x2,y2,z2) ,则
l α .
λ∈R,使得
λ∈R,使得x1=λx2,y1=λy2,z1=λz2.
设设平面 α ,β的法向量 =(x1,y1,z1),=(x2,y2,z2) ,则
α β .
x1x2+y1y2+z1z2=0.
作业布置
作业: P33 练习 第1,2,3题
P42-43 习题1.4 第5,11题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
