鲁教版九年级数学上学期期末总复习反比例函数复习(含答案)
文档属性
| 名称 | 鲁教版九年级数学上学期期末总复习反比例函数复习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 205.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-25 00:00:00 | ||
图片预览

文档简介
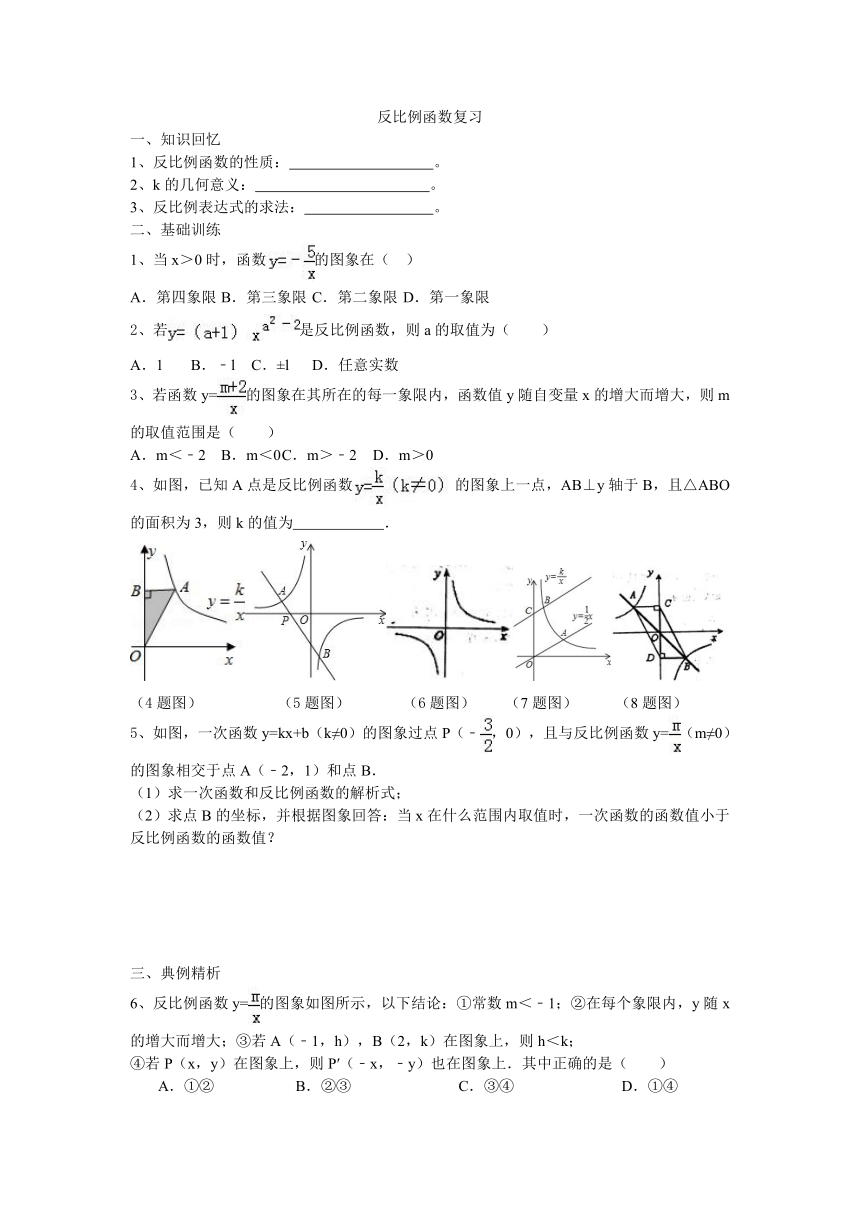
反比例函数复习
一、知识回忆
1、反比例函数的性质: 。
2、k的几何意义: 。
3、反比例表达式的求法: 。
二、基础训练
1、当x>0时,函数的图象在( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
2、若是反比例函数,则a的取值为( )
A.1 B.﹣l C.±l D.任意实数
3、若函数y=的图象在其所在的每一象限内,函数值y随自变量x的增大而增大,则m的取值范围是( )
A.m<﹣2 B.m<0 C.m>﹣2 D.m>0
4、如图,已知A点是反比例函数的图象上一点,AB⊥y轴于B,且△ABO的面积为3,则k的值为 .
(4题图) (5题图) (6题图) (7题图) (8题图)
5、如图,一次函数y=kx+b(k≠0)的图象过点P(﹣,0),且与反比例函数y=(m≠0)的图象相交于点A(﹣2,1)和点B.
(1)求一次函数和反比例函数的解析式;
(2)求点B的坐标,并根据图象回答:当x在什么范围内取值时,一次函数的函数值小于反比例函数的函数值?
三、典例精析
6、反比例函数y=的图象如图所示,以下结论:①常数m<﹣1;②在每个象限内,y随x的增大而增大;③若A(﹣1,h),B(2,k)在图象上,则h<k;
④若P(x,y)在图象上,则P′(﹣x,﹣y)也在图象上.其中正确的是( )
A.①② B. ②③ C. ③④ D. ①④
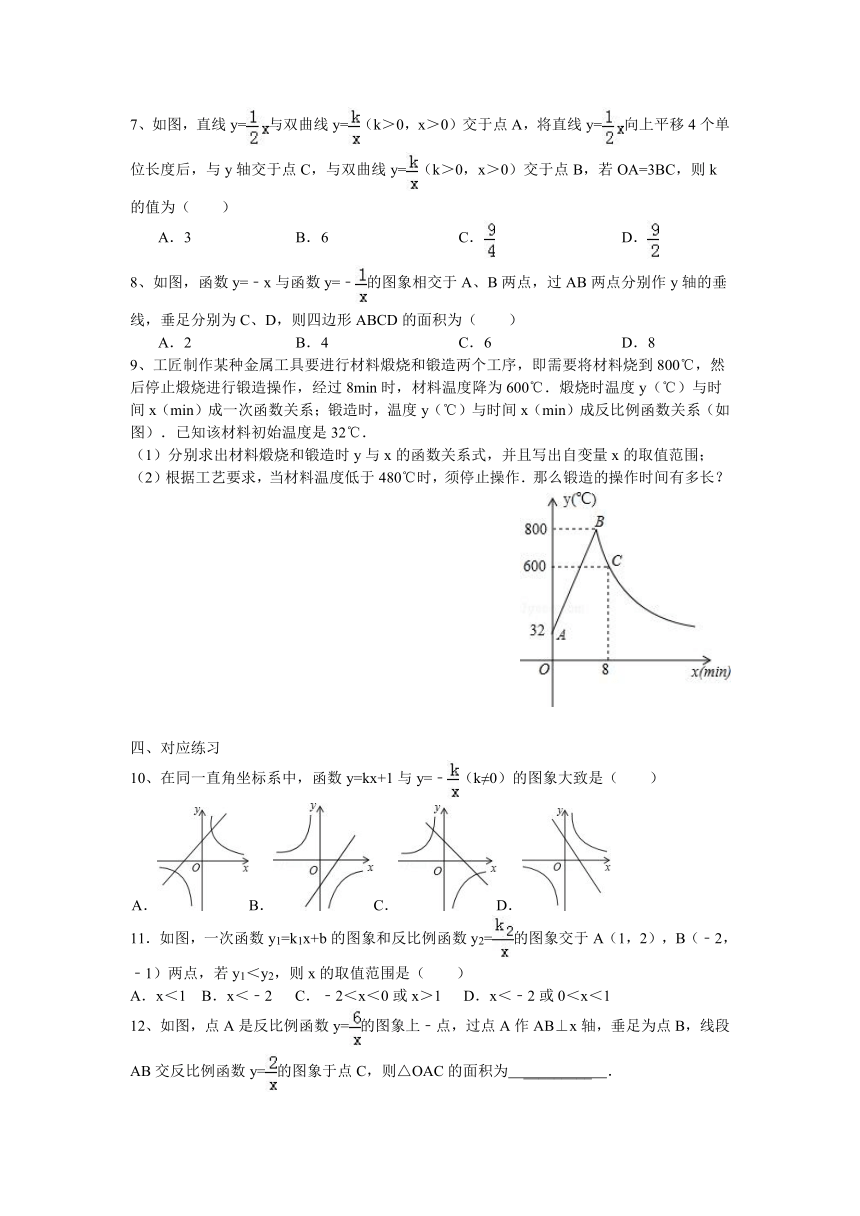
7、如图,直线y=与双曲线y=(k>0,x>0)交于点A,将直线y=向上平移4个单位长度后,与y轴交于点C,与双曲线y=(k>0,x>0)交于点B,若OA=3BC,则k的值为( )
A.3 B. 6 C. D.
8、如图,函数y=﹣x与函数y=﹣的图象相交于A、B两点,过AB两点分别作y轴的垂线,垂足分别为C、D,则四边形ABCD的面积为( )
A.2 B. 4 C. 6 D. 8
9、工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800℃,然后停止煅烧进行锻造操作,经过8min时,材料温度降为600℃.煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图).已知该材料初始温度是32℃.
(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作.那么锻造的操作时间有多长?
四、对应练习
10、在同一直角坐标系中,函数y=kx+1与y=﹣(k≠0)的图象大致是( )
A.B.C.D.
11.如图,一次函数y1=k1x+b的图象和反比例函数y2=的图象交于A(1,2),B(﹣2,﹣1)两点,若y1<y2,则x的取值范围是( )
A.x<1 B.x<﹣2 C.﹣2<x<0或x>1 D.x<﹣2或0<x<1
12、如图,点A是反比例函数y=的图象上﹣点,过点A作AB⊥x轴,垂足为点B,线段AB交反比例函数y=的图象于点C,则△OAC的面积为 _________ .
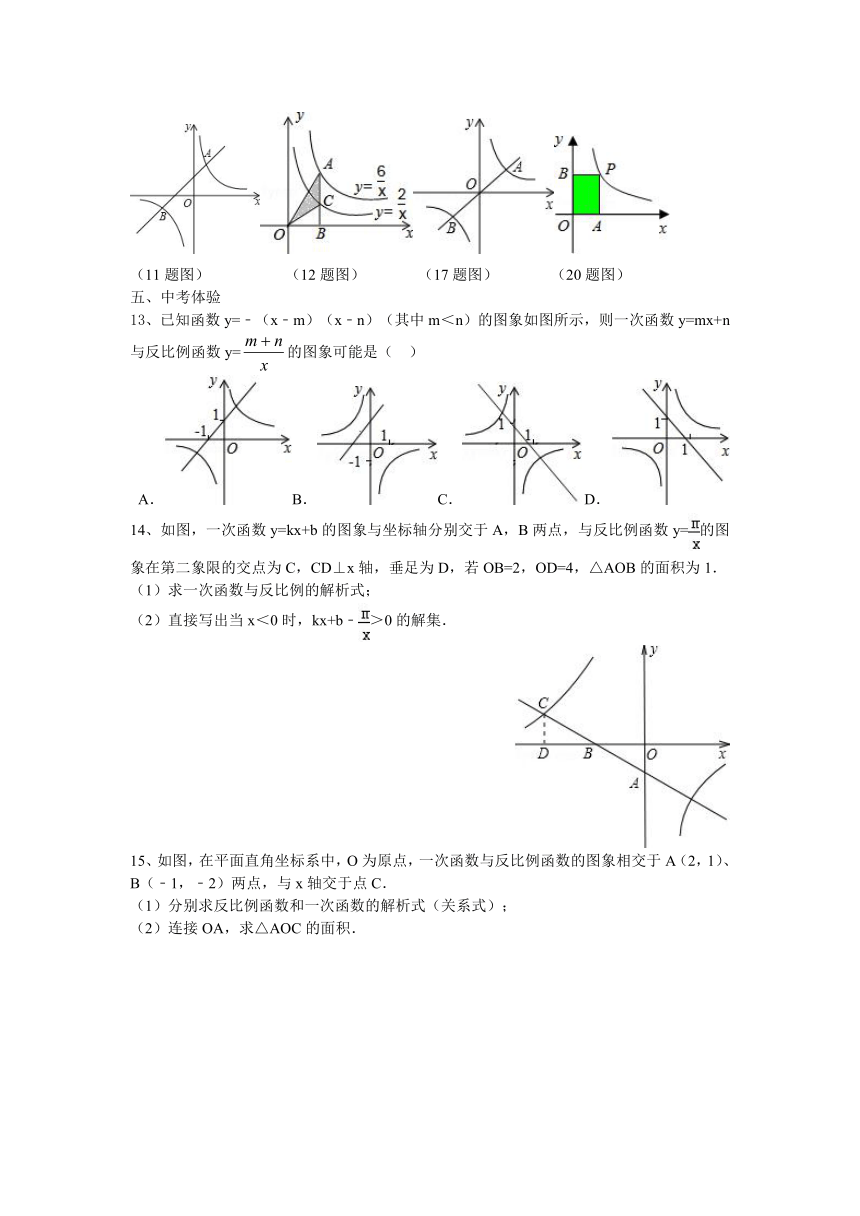
(11题图) (12题图) (17题图) (20题图)
中考体验
13、已知函数y=﹣(x﹣m)(x﹣n)(其中m<n)的图象如图所示,则一次函数y=mx+n与反比例函数y=的图象可能是( )
A.B.C. D.
14、如图,一次函数y=kx+b的图象与坐标轴分别交于A,B两点,与反比例函数y=的图象在第二象限的交点为C,CD⊥x轴,垂足为D,若OB=2,OD=4,△AOB的面积为1.
(1)求一次函数与反比例的解析式;
(2)直接写出当x<0时,kx+b﹣>0的解集.
15、如图,在平面直角坐标系中,O为原点,一次函数与反比例函数的图象相交于A(2,1)、B(﹣1,﹣2)两点,与x轴交于点C.
(1)分别求反比例函数和一次函数的解析式(关系式);
(2)连接OA,求△AOC的面积.
六、当堂测试
16.一次函数y=x+m(m≠0)与反比例函数的图象在同一平面直角坐标系中是( )
A.B.C.D.
17.如图,正比例函数y=k1x与反比例函数y=的图象相交于A、B两点,若点A的坐标为(2,1),则点B的坐标是( )
A.(1,2)B.(﹣2,1) C. (﹣1,﹣2)D.(﹣2,﹣1)
18.对于反比例函数,下列说法正确的是( )
A.图象经过点(1,﹣2) B. 图象在二、四象限
C.当x>0时,y随x的增大而增大 D. 图象关于原点成中心对称
19.对于函数,下列说法错误的是( )
A. 它的图象分布在一、三象限 B. 它的图象既是轴对称图形又是中心对称图形
C. 当x>0时,y的值随x的增大而增大 D. 当x<0时,y的值随x的增大而减小
20.如图,P(x,y)是反比例函数y=的图象在第一象限分支上的一个动点,PA⊥x轴于点A,PB⊥y轴于点B,随着自变量x的增大,矩形OAPB的面积( )
A.不变B.增大 C. 减小D.无法确定
21.若反比例函数的图象上有两点P1(1,y1)和P2(2,y2),那么( )
A.y2<y1<0 B.y1<y2<0 C.y2>y1>0 D.y1>y2>0
22.点(﹣1,y1),(2,y2),(3,y3)均在函数的图象上,则y1,y2,y3的大小关系是( )
A.y3<y2<y1 B.y2<y3<y1 C.y1<y2<y3 D.y1<y3<y2
23、如图,点A(3,n)在双曲线y=上,过点A作AC⊥x轴,垂足为C.线段OA的垂直平分线交OC于点M,则△AMC周长的值是________.
24、已知:如图,反比例函数y=的图象与一次函数y=x+b的图象交于点A(1,4)、点B(﹣4,n).
(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
反比例函数复习参考答案
1、A.2、A;3、A;4、6;
5、解:(1)一次函数y=kx+b(k≠0)的图象过点P(﹣,0)和A(﹣2,1),
∴,解得,∴一次函数的解析式为y=﹣2x﹣3,
反比例函数y=(m≠0)的图象过点A(﹣2,1),∴,解得m=﹣2,
∴反比例函数的解析式为y=﹣;
(2),解得,或,∴B(,﹣4)
由图象可知,当﹣2<x<0或x>时,一次函数的函数值小于反比例函数的函数值.
6、C.7、D.8、D.9、
10、D.11、D.12、2 13、C.
14、解:(1)∵OB=2,△AOB的面积为1。∴B(﹣2,0),OA=1,∴A(0,﹣1)
∴∴∴y=﹣x﹣1
又∵OD=4,CD⊥x轴,∴C(﹣4,y),
将x=﹣4代入y=﹣x﹣1得y=1,∴C(﹣4,1)
∴1=,∴m=﹣4,∴y=﹣,∴反比例函数的解析式为:y=﹣;
(2)当x<0时,kx+b﹣>0的解集是x<﹣4.
15、解:(1)设一次函数解析式为y1=kx+b(k≠0);反比例函数解析式为y2=(a≠0),
∵将A(2,1)、B(﹣1,﹣2)代入y1得:,∴,
∴y1=x﹣1;∵将A(2,1)代入y2得:a=2,∴;
答:反比例函数的解析式是y2=,一次函数的解析式是y1=x﹣1.
(2)∵y1=x﹣1,当y1=0时,x=1,∴C(1,0),∴OC=1,∴S△AOC=×1×1=.
答:△AOC的面积为.
16.C.17.D.18.D.19.C.20.A.21.D.22.D.23、4
24、解:(1)把A点(1,4)分别代入反比例函数y=,一次函数y=x+b,得k=1×4,1+b=4,
解得k=4,b=3,
∴反比例函数的解析式是y=,一次函数解析式是y=x+3;
(2)如图,设直线y=x+3与y轴的交点为C,
当x=﹣4时,y=﹣1,
∴B(﹣4,﹣1),
当x=0时,y=3,
∴C(0,3),
∴S△AOB=S△AOC+S△BOC==;
(3)∵B(﹣4,﹣1),A(1,4),
∴根据图象可知:当x>1或﹣4<x<0时,一次函数值大于反比例函数值.
一、知识回忆
1、反比例函数的性质: 。
2、k的几何意义: 。
3、反比例表达式的求法: 。
二、基础训练
1、当x>0时,函数的图象在( )
A.第四象限 B.第三象限 C.第二象限 D.第一象限
2、若是反比例函数,则a的取值为( )
A.1 B.﹣l C.±l D.任意实数
3、若函数y=的图象在其所在的每一象限内,函数值y随自变量x的增大而增大,则m的取值范围是( )
A.m<﹣2 B.m<0 C.m>﹣2 D.m>0
4、如图,已知A点是反比例函数的图象上一点,AB⊥y轴于B,且△ABO的面积为3,则k的值为 .
(4题图) (5题图) (6题图) (7题图) (8题图)
5、如图,一次函数y=kx+b(k≠0)的图象过点P(﹣,0),且与反比例函数y=(m≠0)的图象相交于点A(﹣2,1)和点B.
(1)求一次函数和反比例函数的解析式;
(2)求点B的坐标,并根据图象回答:当x在什么范围内取值时,一次函数的函数值小于反比例函数的函数值?
三、典例精析
6、反比例函数y=的图象如图所示,以下结论:①常数m<﹣1;②在每个象限内,y随x的增大而增大;③若A(﹣1,h),B(2,k)在图象上,则h<k;
④若P(x,y)在图象上,则P′(﹣x,﹣y)也在图象上.其中正确的是( )
A.①② B. ②③ C. ③④ D. ①④
7、如图,直线y=与双曲线y=(k>0,x>0)交于点A,将直线y=向上平移4个单位长度后,与y轴交于点C,与双曲线y=(k>0,x>0)交于点B,若OA=3BC,则k的值为( )
A.3 B. 6 C. D.
8、如图,函数y=﹣x与函数y=﹣的图象相交于A、B两点,过AB两点分别作y轴的垂线,垂足分别为C、D,则四边形ABCD的面积为( )
A.2 B. 4 C. 6 D. 8
9、工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800℃,然后停止煅烧进行锻造操作,经过8min时,材料温度降为600℃.煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图).已知该材料初始温度是32℃.
(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作.那么锻造的操作时间有多长?
四、对应练习
10、在同一直角坐标系中,函数y=kx+1与y=﹣(k≠0)的图象大致是( )
A.B.C.D.
11.如图,一次函数y1=k1x+b的图象和反比例函数y2=的图象交于A(1,2),B(﹣2,﹣1)两点,若y1<y2,则x的取值范围是( )
A.x<1 B.x<﹣2 C.﹣2<x<0或x>1 D.x<﹣2或0<x<1
12、如图,点A是反比例函数y=的图象上﹣点,过点A作AB⊥x轴,垂足为点B,线段AB交反比例函数y=的图象于点C,则△OAC的面积为 _________ .
(11题图) (12题图) (17题图) (20题图)
中考体验
13、已知函数y=﹣(x﹣m)(x﹣n)(其中m<n)的图象如图所示,则一次函数y=mx+n与反比例函数y=的图象可能是( )
A.B.C. D.
14、如图,一次函数y=kx+b的图象与坐标轴分别交于A,B两点,与反比例函数y=的图象在第二象限的交点为C,CD⊥x轴,垂足为D,若OB=2,OD=4,△AOB的面积为1.
(1)求一次函数与反比例的解析式;
(2)直接写出当x<0时,kx+b﹣>0的解集.
15、如图,在平面直角坐标系中,O为原点,一次函数与反比例函数的图象相交于A(2,1)、B(﹣1,﹣2)两点,与x轴交于点C.
(1)分别求反比例函数和一次函数的解析式(关系式);
(2)连接OA,求△AOC的面积.
六、当堂测试
16.一次函数y=x+m(m≠0)与反比例函数的图象在同一平面直角坐标系中是( )
A.B.C.D.
17.如图,正比例函数y=k1x与反比例函数y=的图象相交于A、B两点,若点A的坐标为(2,1),则点B的坐标是( )
A.(1,2)B.(﹣2,1) C. (﹣1,﹣2)D.(﹣2,﹣1)
18.对于反比例函数,下列说法正确的是( )
A.图象经过点(1,﹣2) B. 图象在二、四象限
C.当x>0时,y随x的增大而增大 D. 图象关于原点成中心对称
19.对于函数,下列说法错误的是( )
A. 它的图象分布在一、三象限 B. 它的图象既是轴对称图形又是中心对称图形
C. 当x>0时,y的值随x的增大而增大 D. 当x<0时,y的值随x的增大而减小
20.如图,P(x,y)是反比例函数y=的图象在第一象限分支上的一个动点,PA⊥x轴于点A,PB⊥y轴于点B,随着自变量x的增大,矩形OAPB的面积( )
A.不变B.增大 C. 减小D.无法确定
21.若反比例函数的图象上有两点P1(1,y1)和P2(2,y2),那么( )
A.y2<y1<0 B.y1<y2<0 C.y2>y1>0 D.y1>y2>0
22.点(﹣1,y1),(2,y2),(3,y3)均在函数的图象上,则y1,y2,y3的大小关系是( )
A.y3<y2<y1 B.y2<y3<y1 C.y1<y2<y3 D.y1<y3<y2
23、如图,点A(3,n)在双曲线y=上,过点A作AC⊥x轴,垂足为C.线段OA的垂直平分线交OC于点M,则△AMC周长的值是________.
24、已知:如图,反比例函数y=的图象与一次函数y=x+b的图象交于点A(1,4)、点B(﹣4,n).
(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
反比例函数复习参考答案
1、A.2、A;3、A;4、6;
5、解:(1)一次函数y=kx+b(k≠0)的图象过点P(﹣,0)和A(﹣2,1),
∴,解得,∴一次函数的解析式为y=﹣2x﹣3,
反比例函数y=(m≠0)的图象过点A(﹣2,1),∴,解得m=﹣2,
∴反比例函数的解析式为y=﹣;
(2),解得,或,∴B(,﹣4)
由图象可知,当﹣2<x<0或x>时,一次函数的函数值小于反比例函数的函数值.
6、C.7、D.8、D.9、
10、D.11、D.12、2 13、C.
14、解:(1)∵OB=2,△AOB的面积为1。∴B(﹣2,0),OA=1,∴A(0,﹣1)
∴∴∴y=﹣x﹣1
又∵OD=4,CD⊥x轴,∴C(﹣4,y),
将x=﹣4代入y=﹣x﹣1得y=1,∴C(﹣4,1)
∴1=,∴m=﹣4,∴y=﹣,∴反比例函数的解析式为:y=﹣;
(2)当x<0时,kx+b﹣>0的解集是x<﹣4.
15、解:(1)设一次函数解析式为y1=kx+b(k≠0);反比例函数解析式为y2=(a≠0),
∵将A(2,1)、B(﹣1,﹣2)代入y1得:,∴,
∴y1=x﹣1;∵将A(2,1)代入y2得:a=2,∴;
答:反比例函数的解析式是y2=,一次函数的解析式是y1=x﹣1.
(2)∵y1=x﹣1,当y1=0时,x=1,∴C(1,0),∴OC=1,∴S△AOC=×1×1=.
答:△AOC的面积为.
16.C.17.D.18.D.19.C.20.A.21.D.22.D.23、4
24、解:(1)把A点(1,4)分别代入反比例函数y=,一次函数y=x+b,得k=1×4,1+b=4,
解得k=4,b=3,
∴反比例函数的解析式是y=,一次函数解析式是y=x+3;
(2)如图,设直线y=x+3与y轴的交点为C,
当x=﹣4时,y=﹣1,
∴B(﹣4,﹣1),
当x=0时,y=3,
∴C(0,3),
∴S△AOB=S△AOC+S△BOC==;
(3)∵B(﹣4,﹣1),A(1,4),
∴根据图象可知:当x>1或﹣4<x<0时,一次函数值大于反比例函数值.
