鲁教版九年级数学上学期期末总复习三角函数复习(含答案)
文档属性
| 名称 | 鲁教版九年级数学上学期期末总复习三角函数复习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 261.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-25 11:21:16 | ||
图片预览

文档简介
鲁教版九年级数学上期末总复习三角函数复习(含答案)
一知识回顾
1、定义: 。
2、特殊值: 。
3、应用: 。
二基础练习
1、在△ABC中,若角A,B满足|cosA﹣|+(1﹣tanB)2=0,则∠C的大小是( )
A.45° B.60° C.75° D.105°
2.如图所示,△ABC的顶点是正方形网格的格点,则sinB的值为( )
A. B. C. D.1
(2题图) (3题图) (4题图) (5题图) (6题图)
3.如图,为安全起见,萌萌拟加长滑梯,将其倾斜角由45°降至30°.已知滑梯AB的长为3m,点D、B、C在同一水平地面上,那么加长后的滑梯AD的长是( )
A.2 B.2 C.3 D.3m
4.如图,马航370失联后,“海巡31”船匀速在印度洋搜救,当它行驶到A处时,发现它的北偏东30°方向有一灯塔B,海巡船继续向北航行4小时后到达C处,发现灯塔B在它的北偏东60°方向.若海巡船继续向北航行,那么要再过多少时间海巡船离灯塔B最近?( )A.1小时 B.2小时 C.小时 D.2小时
三、典例解析
5、如图,点A(t,3)在第一象限,OA与x轴所夹的锐角为α,tanα=,则t的值是( )
A. 1 B. 1.5 C. 2 D. 3
6、如图,在下列网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是( )
A. B. C. D.
7、如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走6m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.
(1)求∠BPQ的度数;
(2)求该电线杆PQ的高度(结果精确到1m).
备用数据:,.
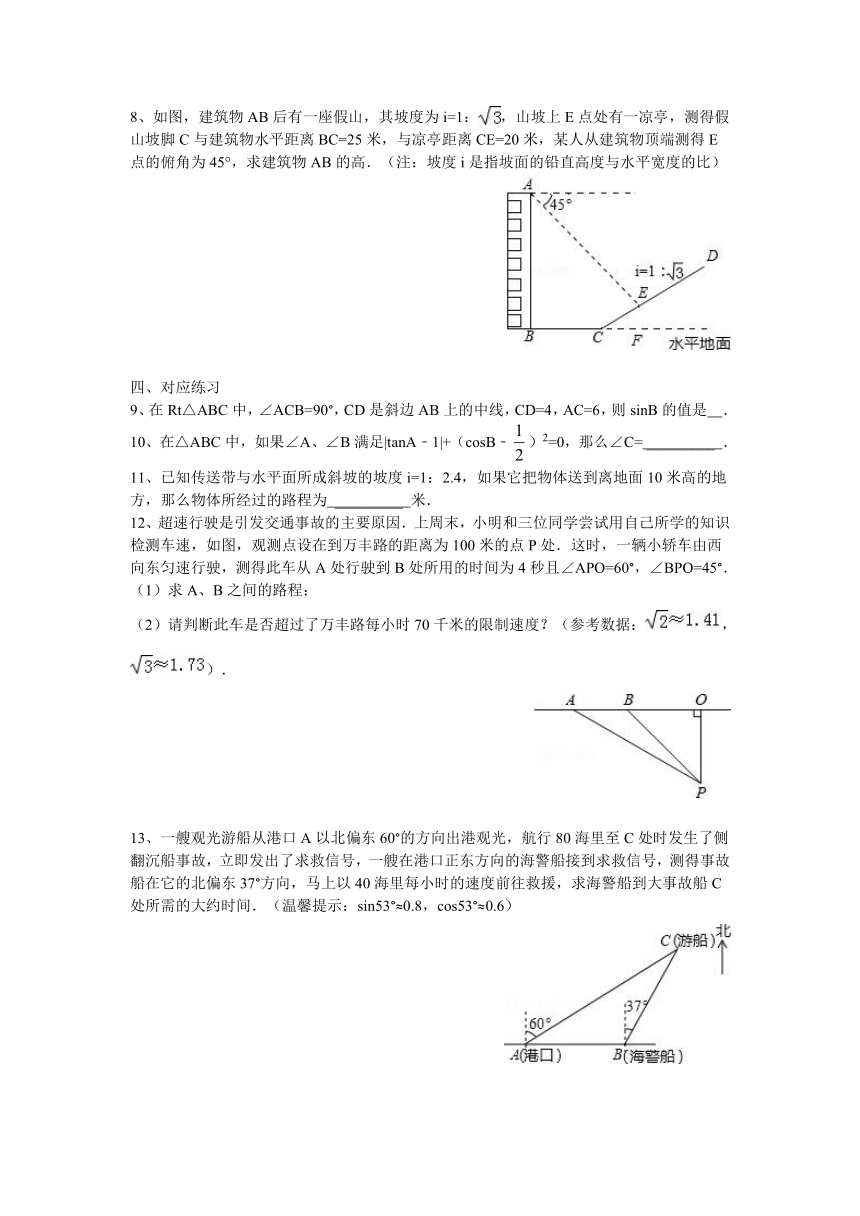
8、如图,建筑物AB后有一座假山,其坡度为i=1:,山坡上E点处有一凉亭,测得假山坡脚C与建筑物水平距离BC=25米,与凉亭距离CE=20米,某人从建筑物顶端测得E点的俯角为45°,求建筑物AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
四、对应练习
9、在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,CD=4,AC=6,则sinB的值是 .
10、在△ABC中,如果∠A、∠B满足|tanA﹣1|+(cosB﹣)2=0,那么∠C= _________ .
11、已知传送带与水平面所成斜坡的坡度i=1:2.4,如果它把物体送到离地面10米高的地方,那么物体所经过的路程为 _________ 米.
12、超速行驶是引发交通事故的主要原因.上周末,小明和三位同学尝试用自己所学的知识检测车速,如图,观测点设在到万丰路的距离为100米的点P处.这时,一辆小轿车由西向东匀速行驶,测得此车从A处行驶到B处所用的时间为4秒且∠APO=60°,∠BPO=45°.
(1)求A、B之间的路程;
(2)请判断此车是否超过了万丰路每小时70千米的限制速度?(参考数据:,).
13、一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)
五、中考体验
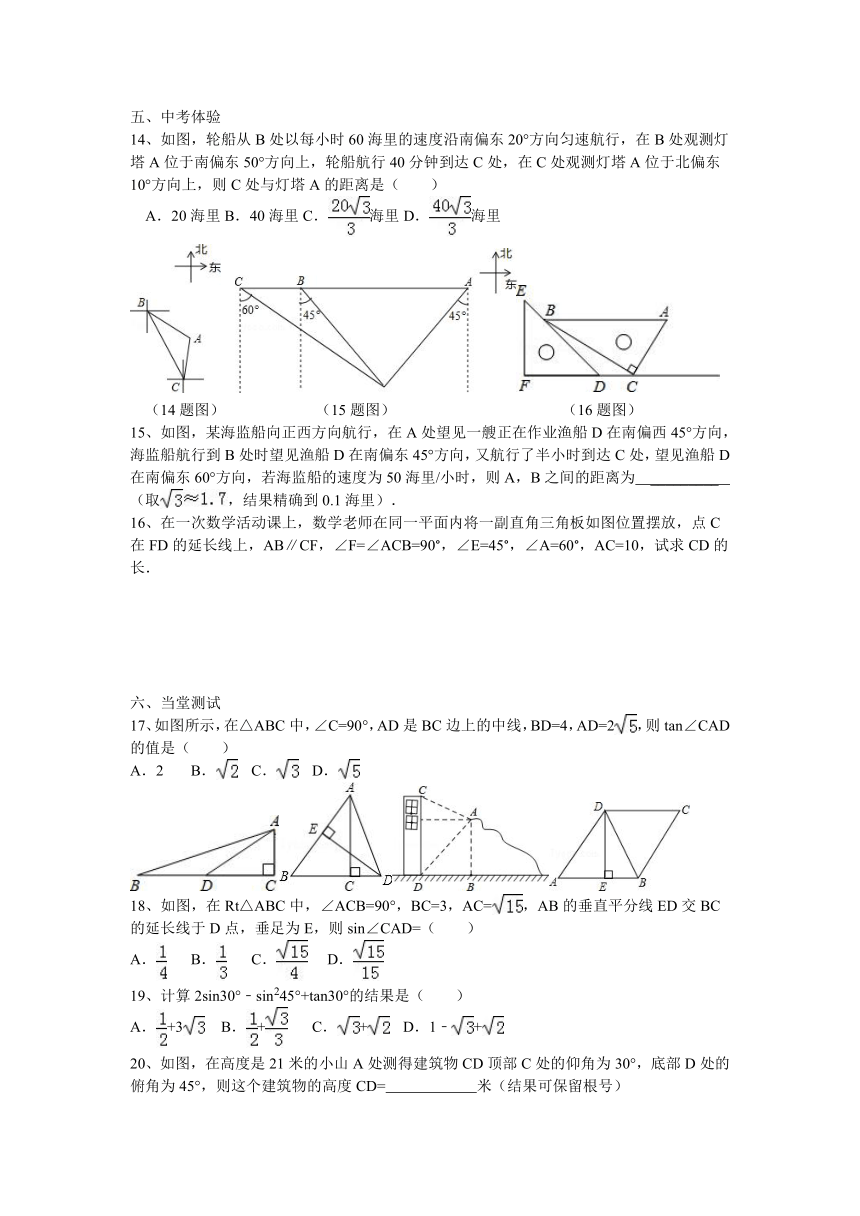
14、如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行40分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是( )
A.20海里B.40海里C.海里D.海里
(14题图) (15题图) (16题图)
15、如图,某海监船向正西方向航行,在A处望见一艘正在作业渔船D在南偏西45°方向,海监船航行到B处时望见渔船D在南偏东45°方向,又航行了半小时到达C处,望见渔船D在南偏东60°方向,若海监船的速度为50海里/小时,则A,B之间的距离为 _________ (取,结果精确到0.1海里).
16、在一次数学活动课上,数学老师在同一平面内将一副直角三角板如图位置摆放,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,试求CD的长.
六、当堂测试
17、如图所示,在△ABC中,∠C=90°,AD是BC边上的中线,BD=4,AD=2,则tan∠CAD的值是( )
A.2 B. C. D.
18、如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=,AB的垂直平分线ED交BC的延长线于D点,垂足为E,则sin∠CAD=( )
A. B. C. D.
19、计算2sin30°﹣sin245°+tan30°的结果是( )
A.+3 B.+ C.+ D.1﹣+
20、如图,在高度是21米的小山A处测得建筑物CD顶部C处的仰角为30°,底部D处的俯角为45°,则这个建筑物的高度CD= 米(结果可保留根号)
21、如图,在菱形ABCD中,DE⊥AB于点E,cosA=,BE=4,则tan∠DBE的值是 .
22、如图,在△ABC中,∠C=90°,∠B=60°,D是AC上一点,DE⊥AB于E,且CD=2,DE=1,则BC的长为 .
23、如图,美丽的徒骇河宛如一条玉带穿城而过,沿河两岸的滨河大道和风景带成为我市的一道新景观.在数学课外实践活动中,小亮在河西岸滨河大道一段AC上的A,B两点处,利用测角仪分别对东岸的观景台D进行了测量,分别测得∠DAC=60°,∠DBC=75°.又已知AB=100米,求观景台D到徒骇河西岸AC的距离约为多少米(精确到1米).(tan60°≈1.73,tan75°≈3.73)
24、如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
鲁教版九年级数学上期末总复习三角函数复习参考答案
1、D.2、B.3、C.4、B.5、C.6、D.
7、解:延长PQ交直线AB于点E,
(1)∠BPQ=90°﹣60°=30°;
(2)设PE=x米.
在直角△APE中,∠A=45°,则AE=PE=x米;
∵∠PBE=60°∴∠BPE=30°
在直角△BPE中,BE=PE=x米,
∵AB=AE﹣BE=6米,则x﹣x=6,解得:x=9+3.则BE=(3+3)米.
在直角△BEQ中,QE=BE=(3+3)=(3+)米.
∴PQ=PE﹣QE=9+3﹣(3+)=6+2≈9(米).
答:电线杆PQ的高度约9米.
8、解:过点E作EF⊥BC于点F,过点E作EN⊥AB于点N,
∵建筑物AB后有一座假山,其坡度为i=1:,
∴设EF=x,则FC=x,
∵CE=20米,
∴x2+(x)2=400,
解得:x=10,
则FC=10m,
∵BC=25m,∴BF=NE=(25+10)m,
∴AB=AN+BN=NE+EF=10+25+10=(35+10)m,
答:建筑物AB的高为(35+10)m.
9、 .10. 75° 11. 26
12、解:(1)在Rt△BOP中,∠BOP=90°,∵∠BPO=45°,OP=100,∴OB=OP=100.
在Rt△AOP中,∠AOP=90°,∵∠APO=60°,
∴AO=OP tan∠APO.∴A0=100,AB=100(﹣1)(米);
(2)∵此车的速度==25(﹣1)≈25×0.73=18.25米/秒,
70千米/小时=≈19.4米/秒,18.25米/秒<19.4米/秒,
∴此车没有超过了万丰路每小时70千米的限制速度.
13、解:如图,过点C作CD⊥AB交AB延长线于D.
在Rt△ACD中,
∵∠ADC=90°,∠CAD=30°,AC=80海里,∴CD=AC=40海里.
在Rt△CBD中,∵∠CDB=90°,∠CBD=90°﹣37°=53°,
∴BC=≈=50(海里),
∴海警船到大事故船C处所需的时间大约为:50÷40=(小时).
14、 D.15、 67.5
16、解:过点B作BM⊥FD于点M,
在△ACB中,∠ACB=90°,∠A=60°,AC=10,
∴∠ABC=30°,BC=AC tan60°=10,
∵AB∥CF,∴∠BCM=∠ABC=30°.∴BM=BC sin30°=10×=5,
CM=BC cos30°=10×=15,
在△EFD中,∠F=90°,∠E=45°,∴∠EDF=45°,∴MD=BM=5,
∴CD=CM﹣MD=15﹣5.
17、A 18、A 19、B 20、21+7 21、2 22、
23、解:如图,过点D作DE⊥AC于点E.
∵在Rt△EAD中,∠DAE=60°,∴tan60°=,∴AE=
同理,在Rt△EBD中,得到EB=.
又∵AB=100米,∴AE﹣EB=100米,即﹣=100.
则ED=≈≈323(米).
答:观景台D到徒骇河西岸AC的距离约为323米.
24、解:(1)根据题意得:BD∥AE,
∴∠ADB=∠EAD=45°,
∵∠ABD=90°,
∴∠BAD=∠ADB=45°,
∴BD=AB=60,
∴两建筑物底部之间水平距离BD的长度为60米;
(2)延长AE、DC交于点F,根据题意得四边形ABDF为正方形,
∴AF=BD=DF=60,
在Rt△AFC中,∠FAC=30°,
∴CF=AF tan∠FAC=60×=20,
又∵FD=60,
∴CD=60﹣20,
∴建筑物CD的高度为(60﹣20)米.
一知识回顾
1、定义: 。
2、特殊值: 。
3、应用: 。
二基础练习
1、在△ABC中,若角A,B满足|cosA﹣|+(1﹣tanB)2=0,则∠C的大小是( )
A.45° B.60° C.75° D.105°
2.如图所示,△ABC的顶点是正方形网格的格点,则sinB的值为( )
A. B. C. D.1
(2题图) (3题图) (4题图) (5题图) (6题图)
3.如图,为安全起见,萌萌拟加长滑梯,将其倾斜角由45°降至30°.已知滑梯AB的长为3m,点D、B、C在同一水平地面上,那么加长后的滑梯AD的长是( )
A.2 B.2 C.3 D.3m
4.如图,马航370失联后,“海巡31”船匀速在印度洋搜救,当它行驶到A处时,发现它的北偏东30°方向有一灯塔B,海巡船继续向北航行4小时后到达C处,发现灯塔B在它的北偏东60°方向.若海巡船继续向北航行,那么要再过多少时间海巡船离灯塔B最近?( )A.1小时 B.2小时 C.小时 D.2小时
三、典例解析
5、如图,点A(t,3)在第一象限,OA与x轴所夹的锐角为α,tanα=,则t的值是( )
A. 1 B. 1.5 C. 2 D. 3
6、如图,在下列网格中,小正方形的边长均为1,点A、B、O都在格点上,则∠AOB的正弦值是( )
A. B. C. D.
7、如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走6m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.
(1)求∠BPQ的度数;
(2)求该电线杆PQ的高度(结果精确到1m).
备用数据:,.
8、如图,建筑物AB后有一座假山,其坡度为i=1:,山坡上E点处有一凉亭,测得假山坡脚C与建筑物水平距离BC=25米,与凉亭距离CE=20米,某人从建筑物顶端测得E点的俯角为45°,求建筑物AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
四、对应练习
9、在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,CD=4,AC=6,则sinB的值是 .
10、在△ABC中,如果∠A、∠B满足|tanA﹣1|+(cosB﹣)2=0,那么∠C= _________ .
11、已知传送带与水平面所成斜坡的坡度i=1:2.4,如果它把物体送到离地面10米高的地方,那么物体所经过的路程为 _________ 米.
12、超速行驶是引发交通事故的主要原因.上周末,小明和三位同学尝试用自己所学的知识检测车速,如图,观测点设在到万丰路的距离为100米的点P处.这时,一辆小轿车由西向东匀速行驶,测得此车从A处行驶到B处所用的时间为4秒且∠APO=60°,∠BPO=45°.
(1)求A、B之间的路程;
(2)请判断此车是否超过了万丰路每小时70千米的限制速度?(参考数据:,).
13、一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)
五、中考体验
14、如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行40分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是( )
A.20海里B.40海里C.海里D.海里
(14题图) (15题图) (16题图)
15、如图,某海监船向正西方向航行,在A处望见一艘正在作业渔船D在南偏西45°方向,海监船航行到B处时望见渔船D在南偏东45°方向,又航行了半小时到达C处,望见渔船D在南偏东60°方向,若海监船的速度为50海里/小时,则A,B之间的距离为 _________ (取,结果精确到0.1海里).
16、在一次数学活动课上,数学老师在同一平面内将一副直角三角板如图位置摆放,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,试求CD的长.
六、当堂测试
17、如图所示,在△ABC中,∠C=90°,AD是BC边上的中线,BD=4,AD=2,则tan∠CAD的值是( )
A.2 B. C. D.
18、如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=,AB的垂直平分线ED交BC的延长线于D点,垂足为E,则sin∠CAD=( )
A. B. C. D.
19、计算2sin30°﹣sin245°+tan30°的结果是( )
A.+3 B.+ C.+ D.1﹣+
20、如图,在高度是21米的小山A处测得建筑物CD顶部C处的仰角为30°,底部D处的俯角为45°,则这个建筑物的高度CD= 米(结果可保留根号)
21、如图,在菱形ABCD中,DE⊥AB于点E,cosA=,BE=4,则tan∠DBE的值是 .
22、如图,在△ABC中,∠C=90°,∠B=60°,D是AC上一点,DE⊥AB于E,且CD=2,DE=1,则BC的长为 .
23、如图,美丽的徒骇河宛如一条玉带穿城而过,沿河两岸的滨河大道和风景带成为我市的一道新景观.在数学课外实践活动中,小亮在河西岸滨河大道一段AC上的A,B两点处,利用测角仪分别对东岸的观景台D进行了测量,分别测得∠DAC=60°,∠DBC=75°.又已知AB=100米,求观景台D到徒骇河西岸AC的距离约为多少米(精确到1米).(tan60°≈1.73,tan75°≈3.73)
24、如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).
鲁教版九年级数学上期末总复习三角函数复习参考答案
1、D.2、B.3、C.4、B.5、C.6、D.
7、解:延长PQ交直线AB于点E,
(1)∠BPQ=90°﹣60°=30°;
(2)设PE=x米.
在直角△APE中,∠A=45°,则AE=PE=x米;
∵∠PBE=60°∴∠BPE=30°
在直角△BPE中,BE=PE=x米,
∵AB=AE﹣BE=6米,则x﹣x=6,解得:x=9+3.则BE=(3+3)米.
在直角△BEQ中,QE=BE=(3+3)=(3+)米.
∴PQ=PE﹣QE=9+3﹣(3+)=6+2≈9(米).
答:电线杆PQ的高度约9米.
8、解:过点E作EF⊥BC于点F,过点E作EN⊥AB于点N,
∵建筑物AB后有一座假山,其坡度为i=1:,
∴设EF=x,则FC=x,
∵CE=20米,
∴x2+(x)2=400,
解得:x=10,
则FC=10m,
∵BC=25m,∴BF=NE=(25+10)m,
∴AB=AN+BN=NE+EF=10+25+10=(35+10)m,
答:建筑物AB的高为(35+10)m.
9、 .10. 75° 11. 26
12、解:(1)在Rt△BOP中,∠BOP=90°,∵∠BPO=45°,OP=100,∴OB=OP=100.
在Rt△AOP中,∠AOP=90°,∵∠APO=60°,
∴AO=OP tan∠APO.∴A0=100,AB=100(﹣1)(米);
(2)∵此车的速度==25(﹣1)≈25×0.73=18.25米/秒,
70千米/小时=≈19.4米/秒,18.25米/秒<19.4米/秒,
∴此车没有超过了万丰路每小时70千米的限制速度.
13、解:如图,过点C作CD⊥AB交AB延长线于D.
在Rt△ACD中,
∵∠ADC=90°,∠CAD=30°,AC=80海里,∴CD=AC=40海里.
在Rt△CBD中,∵∠CDB=90°,∠CBD=90°﹣37°=53°,
∴BC=≈=50(海里),
∴海警船到大事故船C处所需的时间大约为:50÷40=(小时).
14、 D.15、 67.5
16、解:过点B作BM⊥FD于点M,
在△ACB中,∠ACB=90°,∠A=60°,AC=10,
∴∠ABC=30°,BC=AC tan60°=10,
∵AB∥CF,∴∠BCM=∠ABC=30°.∴BM=BC sin30°=10×=5,
CM=BC cos30°=10×=15,
在△EFD中,∠F=90°,∠E=45°,∴∠EDF=45°,∴MD=BM=5,
∴CD=CM﹣MD=15﹣5.
17、A 18、A 19、B 20、21+7 21、2 22、
23、解:如图,过点D作DE⊥AC于点E.
∵在Rt△EAD中,∠DAE=60°,∴tan60°=,∴AE=
同理,在Rt△EBD中,得到EB=.
又∵AB=100米,∴AE﹣EB=100米,即﹣=100.
则ED=≈≈323(米).
答:观景台D到徒骇河西岸AC的距离约为323米.
24、解:(1)根据题意得:BD∥AE,
∴∠ADB=∠EAD=45°,
∵∠ABD=90°,
∴∠BAD=∠ADB=45°,
∴BD=AB=60,
∴两建筑物底部之间水平距离BD的长度为60米;
(2)延长AE、DC交于点F,根据题意得四边形ABDF为正方形,
∴AF=BD=DF=60,
在Rt△AFC中,∠FAC=30°,
∴CF=AF tan∠FAC=60×=20,
又∵FD=60,
∴CD=60﹣20,
∴建筑物CD的高度为(60﹣20)米.
