北师大版九年级上第一章特殊平行四边形1.3中点四边形专题课件(共33张PPT)
文档属性
| 名称 | 北师大版九年级上第一章特殊平行四边形1.3中点四边形专题课件(共33张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 224.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-26 00:00:00 | ||
图片预览

文档简介
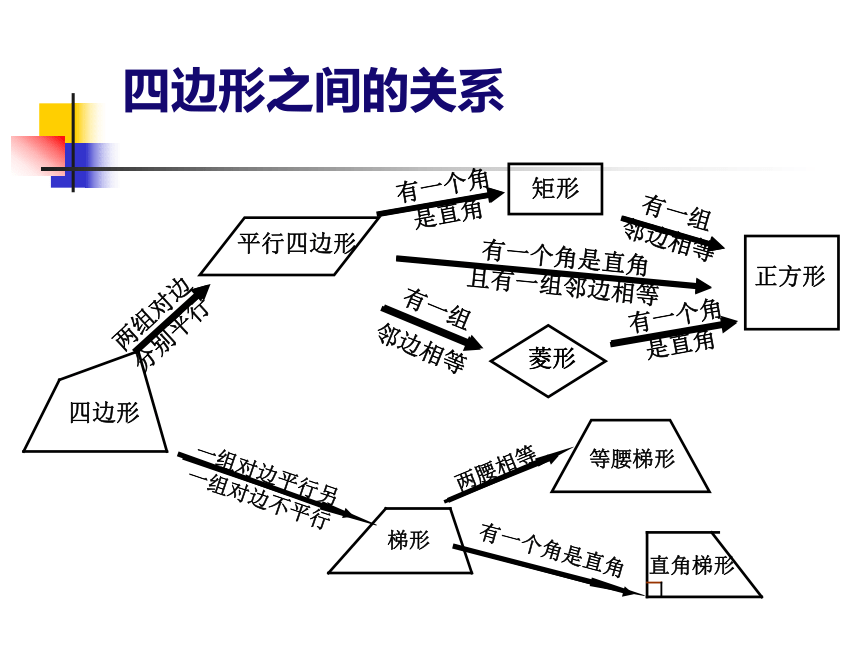
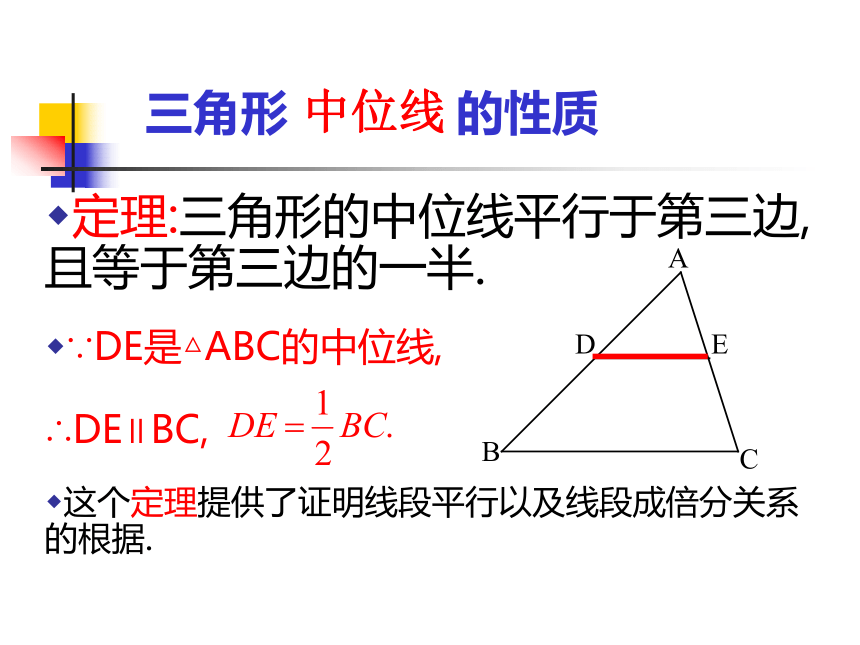
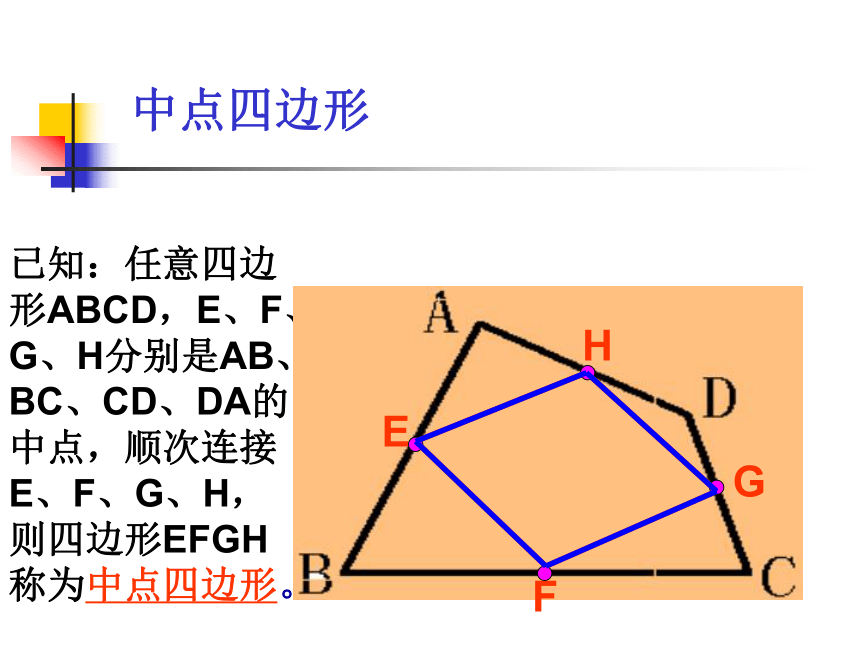
课件33张PPT。特殊的平行四边形(三)四边形之间的关系三角形 的性质定理:三角形的中位线平行于第三边,且等于第三边的一半.这个定理提供了证明线段平行以及线段成倍分关系的根据.∵DE是△ABC的中位线,∴DE∥BC,中位线中点四边形已知:任意四边形ABCD,E、F、G、H分别是AB、BC、CD、DA的中点,顺次连接E、F、G、H,则四边形EFGH称为中点四边形。HGFE练习1:
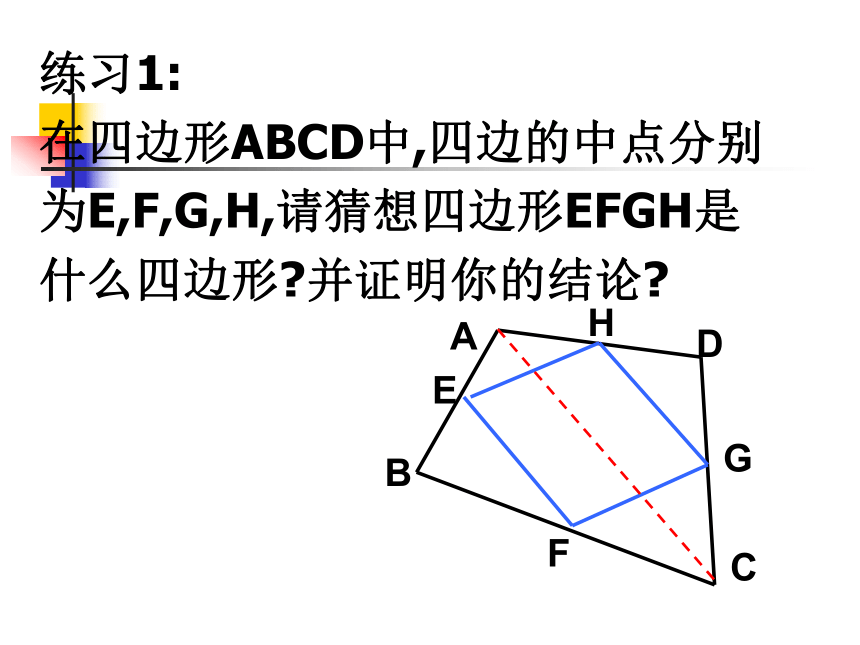
在四边形ABCD中,四边的中点分别
为E,F,G,H,请猜想四边形EFGH是
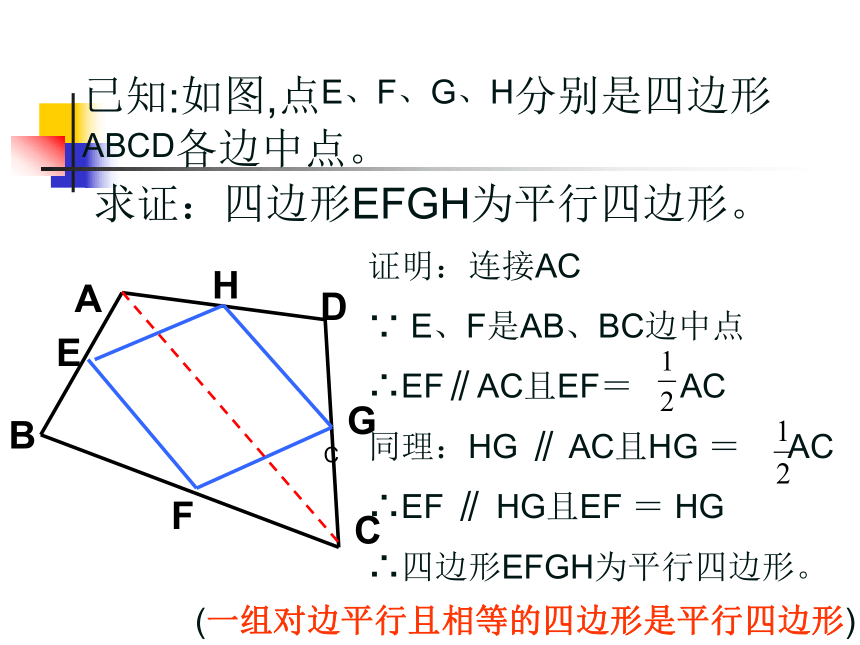
什么四边形?并证明你的结论?已知:如图,点E、F、G、H分别是四边形ABCD各边中点。求证:四边形EFGH为平行四边形。证明:连接AC
∵ E、F是AB、BC边中点
∴EF∥AC且EF= AC
同理:HG ∥ AC且HG = AC
∴EF ∥ HG且EF = HG
∴四边形EFGH为平行四边形。C(一组对边平行且相等的四边形是平行四边形)EFGH结论1:
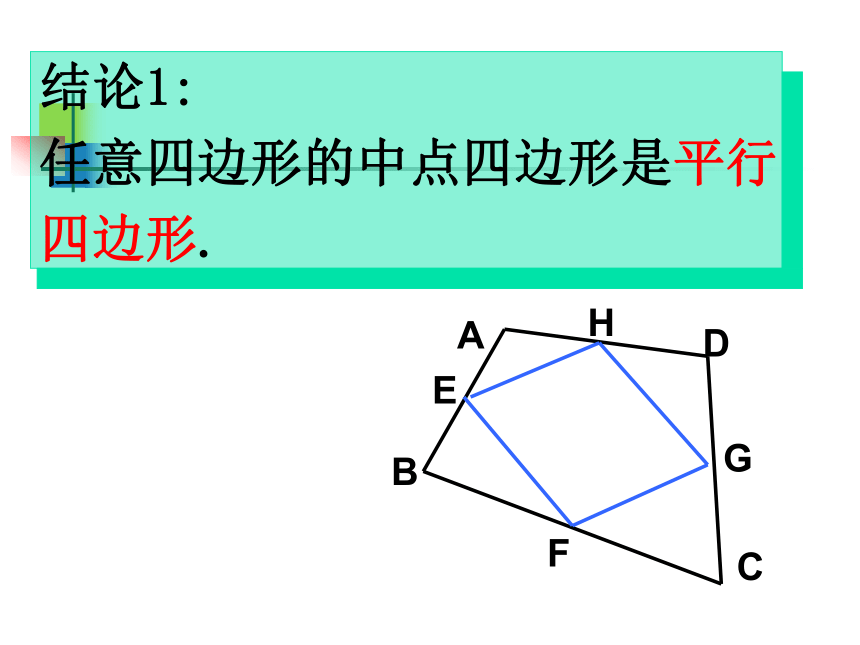
任意四边形的中点四边形是平行
四边形.练习1:
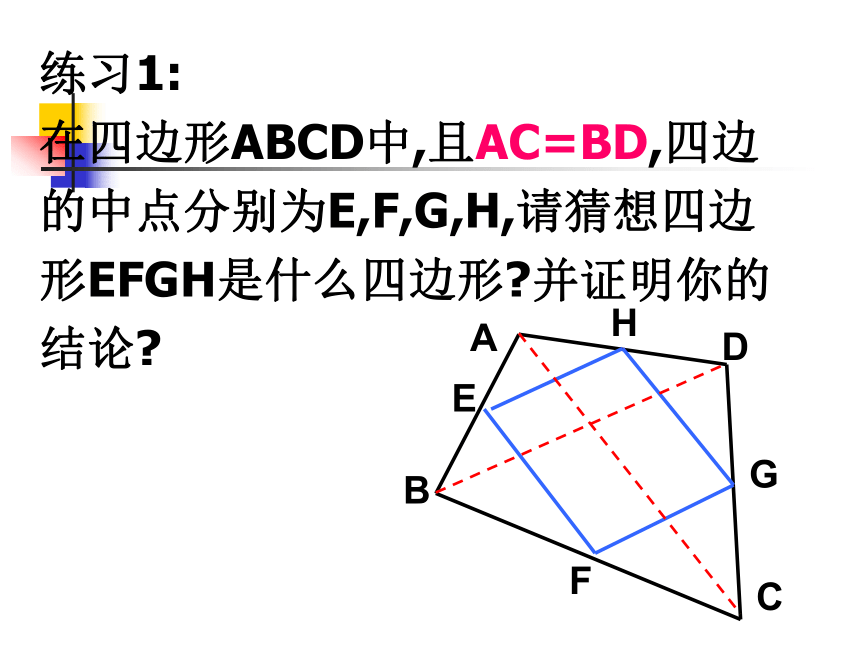
在四边形ABCD中,且AC=BD,四边
的中点分别为E,F,G,H,请猜想四边
形EFGH是什么四边形?并证明你的
结论?练习1:
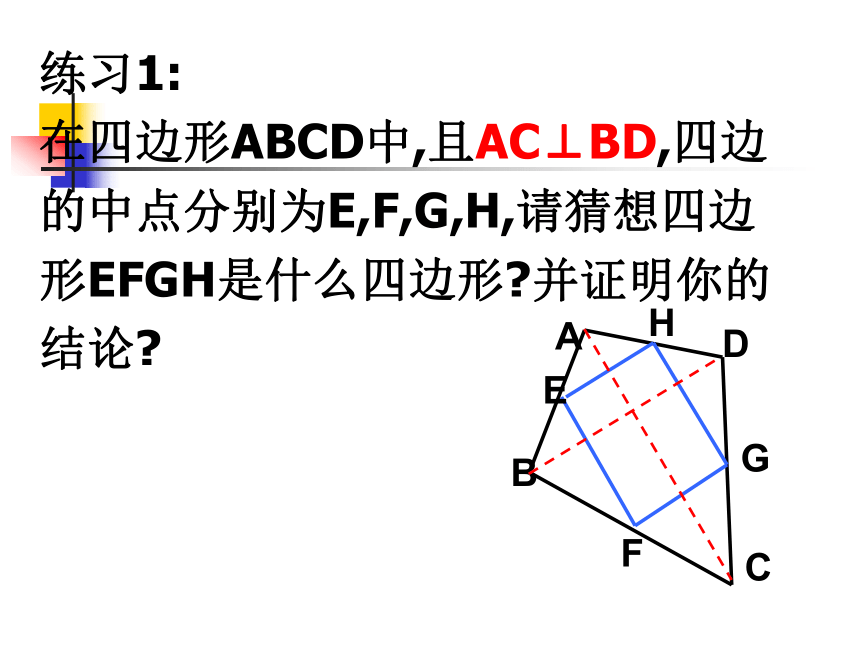
在四边形ABCD中,且AC⊥BD,四边
的中点分别为E,F,G,H,请猜想四边
形EFGH是什么四边形?并证明你的
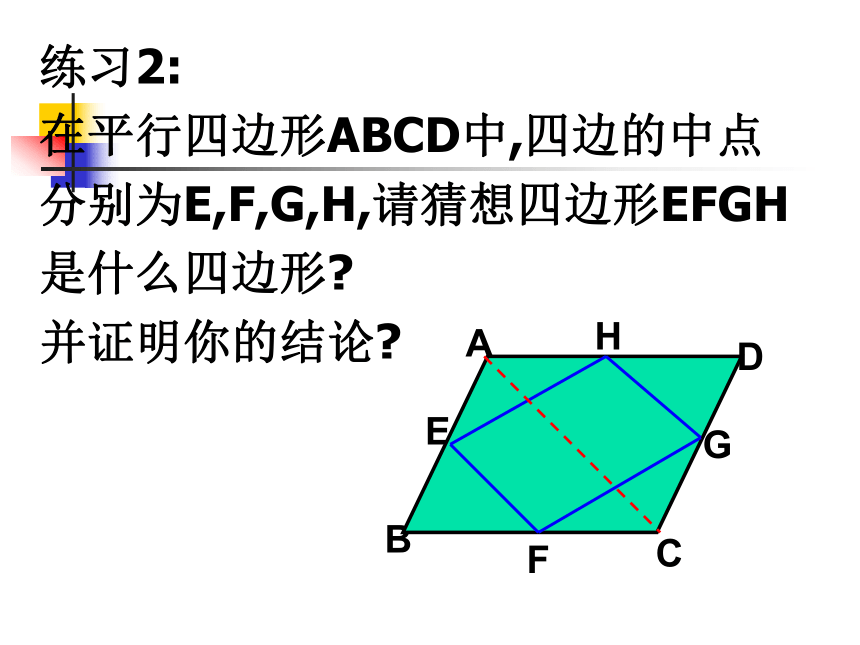
结论?练习2:
在平行四边形ABCD中,四边的中点
分别为E,F,G,H,请猜想四边形EFGH
是什么四边形?
并证明你的结论?ABCDEFGH结论2:
平行四边形的中点四边形是平行四边形.练习3:
在矩形ABCD中,四边的中点分别为
E,F,G,H,请猜想四边形EFGH是什么
四边形?并证明你的结论?ABCDEFGH结论3:
矩形的中点四边形是菱形.ABCDEFGH练习4:
在菱形ABCD中,四边的中点分别为
E,F,G,H,请猜想四边形EFGH是什么
四边形?并证明你的结论?ABCDEFGH结论4:
菱形的中点四边形是矩形.ABCDEFGH练习5:
在正方形ABCD中,四边的中点分别
为E,F,G,H,请猜想四边形EFGH是什
么四边形?并证明你的结论?ABCDEFGH结论5:
正方形的中点四边形是正方形.ABCDEFGH
在等腰梯形ABCD中,四边的中点分
别为E,F,G,H,请猜想四边形EFGH是
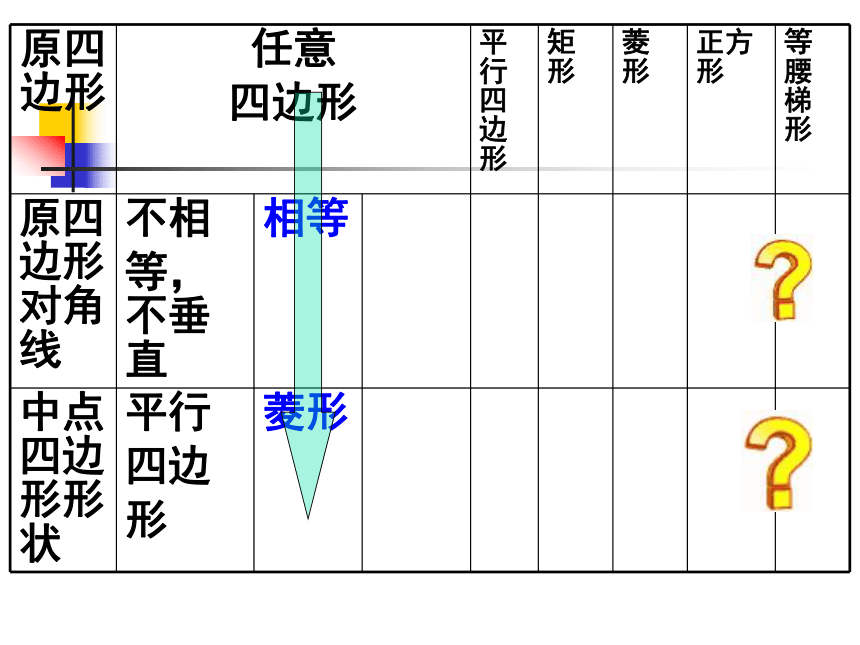
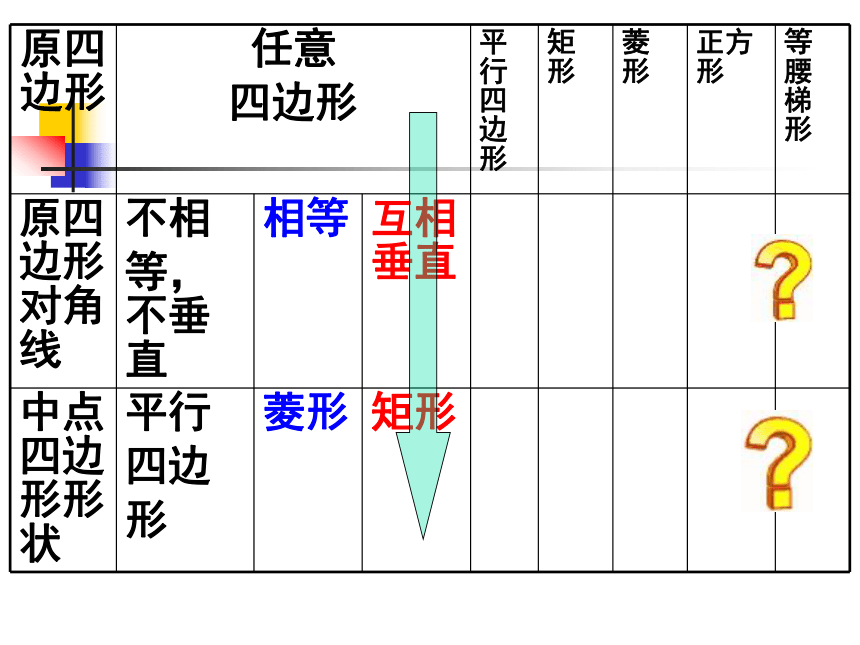
什么四边形?并证明你的结论?ABCDEFGH 依次连接四边形四边中点得到的图形的形状与哪些线段有关系?有怎样的关系?4、当原四边形对角线相等且互相垂直时,四边形
各边中点所得到的新四边形是正方形。3、当原四边形对角线 相等 时, 四边形
各边中点所得到的新四边形是菱形。2、当原四边形对角线 互相垂直时, 四边形
各边中点所得到的新四边形是矩形。1、当原四边形对角线不相等且不垂直时,四边形
各边中点所得到的新四边形是平行四边形。1.如图,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点,请添加一个条件,使四边形EFGH为菱形,并说明理由。
解:添加的条件_______
巩固练习2、选择
四边形四边中点依次连接能得到的图形
是矩形,则原四边形是( )
A、矩形
B、菱形
C、正方形
D、对角线垂直的四边形
巩固练习驶向胜利的彼岸四边形ABCD中,AC=6,BD=8,且AC⊥BD,
顺次连接四边ABCD的中点得到四边形A1B1C1D1,依次类推,得到四边形AnBnCnDn;挑战自我驶向胜利的彼岸四边形ABCD中,AC=6,BD=8,且AC⊥BD,
(1)四边形A1B1C1D1是___,四边形A2B2C2D2是___,
四边形A11B11C11D11是____;矩形矩形菱形挑战自我驶向胜利的彼岸四边形ABCD中,AC=6,BD=8,且AC⊥BD,
(2)四边形A1B1C1D1的面积是_____,
四边形A2B2C2D2的面积是_____。
(3)四边形AnBnCnDn的
面积是________;126挑战自我24/2n驶向胜利的彼岸四边形ABCD中,AC=6,BD=8,且AC⊥BD,
(4)四边形A1B1C1D1的周长是_____。
四边形A2B2C2D2的周长是_____。
四边形A3B3C3D3的周长是_____。
四边形A4B4C4D4的周长是_______;14107挑战自我5这一节课你学到了什么?1、中点四边形的定义;
2、中点四边形的形状与原四边形的对角线的关系。谢谢指导!
在四边形ABCD中,四边的中点分别
为E,F,G,H,请猜想四边形EFGH是
什么四边形?并证明你的结论?已知:如图,点E、F、G、H分别是四边形ABCD各边中点。求证:四边形EFGH为平行四边形。证明:连接AC
∵ E、F是AB、BC边中点
∴EF∥AC且EF= AC
同理:HG ∥ AC且HG = AC
∴EF ∥ HG且EF = HG
∴四边形EFGH为平行四边形。C(一组对边平行且相等的四边形是平行四边形)EFGH结论1:
任意四边形的中点四边形是平行
四边形.练习1:
在四边形ABCD中,且AC=BD,四边
的中点分别为E,F,G,H,请猜想四边
形EFGH是什么四边形?并证明你的
结论?练习1:
在四边形ABCD中,且AC⊥BD,四边
的中点分别为E,F,G,H,请猜想四边
形EFGH是什么四边形?并证明你的
结论?练习2:
在平行四边形ABCD中,四边的中点
分别为E,F,G,H,请猜想四边形EFGH
是什么四边形?
并证明你的结论?ABCDEFGH结论2:
平行四边形的中点四边形是平行四边形.练习3:
在矩形ABCD中,四边的中点分别为
E,F,G,H,请猜想四边形EFGH是什么
四边形?并证明你的结论?ABCDEFGH结论3:
矩形的中点四边形是菱形.ABCDEFGH练习4:
在菱形ABCD中,四边的中点分别为
E,F,G,H,请猜想四边形EFGH是什么
四边形?并证明你的结论?ABCDEFGH结论4:
菱形的中点四边形是矩形.ABCDEFGH练习5:
在正方形ABCD中,四边的中点分别
为E,F,G,H,请猜想四边形EFGH是什
么四边形?并证明你的结论?ABCDEFGH结论5:
正方形的中点四边形是正方形.ABCDEFGH
在等腰梯形ABCD中,四边的中点分
别为E,F,G,H,请猜想四边形EFGH是
什么四边形?并证明你的结论?ABCDEFGH 依次连接四边形四边中点得到的图形的形状与哪些线段有关系?有怎样的关系?4、当原四边形对角线相等且互相垂直时,四边形
各边中点所得到的新四边形是正方形。3、当原四边形对角线 相等 时, 四边形
各边中点所得到的新四边形是菱形。2、当原四边形对角线 互相垂直时, 四边形
各边中点所得到的新四边形是矩形。1、当原四边形对角线不相等且不垂直时,四边形
各边中点所得到的新四边形是平行四边形。1.如图,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点,请添加一个条件,使四边形EFGH为菱形,并说明理由。
解:添加的条件_______
巩固练习2、选择
四边形四边中点依次连接能得到的图形
是矩形,则原四边形是( )
A、矩形
B、菱形
C、正方形
D、对角线垂直的四边形
巩固练习驶向胜利的彼岸四边形ABCD中,AC=6,BD=8,且AC⊥BD,
顺次连接四边ABCD的中点得到四边形A1B1C1D1,依次类推,得到四边形AnBnCnDn;挑战自我驶向胜利的彼岸四边形ABCD中,AC=6,BD=8,且AC⊥BD,
(1)四边形A1B1C1D1是___,四边形A2B2C2D2是___,
四边形A11B11C11D11是____;矩形矩形菱形挑战自我驶向胜利的彼岸四边形ABCD中,AC=6,BD=8,且AC⊥BD,
(2)四边形A1B1C1D1的面积是_____,
四边形A2B2C2D2的面积是_____。
(3)四边形AnBnCnDn的
面积是________;126挑战自我24/2n驶向胜利的彼岸四边形ABCD中,AC=6,BD=8,且AC⊥BD,
(4)四边形A1B1C1D1的周长是_____。
四边形A2B2C2D2的周长是_____。
四边形A3B3C3D3的周长是_____。
四边形A4B4C4D4的周长是_______;14107挑战自我5这一节课你学到了什么?1、中点四边形的定义;
2、中点四边形的形状与原四边形的对角线的关系。谢谢指导!
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
