2023-2024学年度第二学期吉林省白城市大安市期末统考七年级数学(含答案)
文档属性
| 名称 | 2023-2024学年度第二学期吉林省白城市大安市期末统考七年级数学(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 555.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-10 08:44:05 | ||
图片预览



文档简介
七年级第二学期期末教学质量检测试题
——数 学——
题号 一 二 三 四 五 六 得分
得分
一、选择题(每小题2分,共12分)
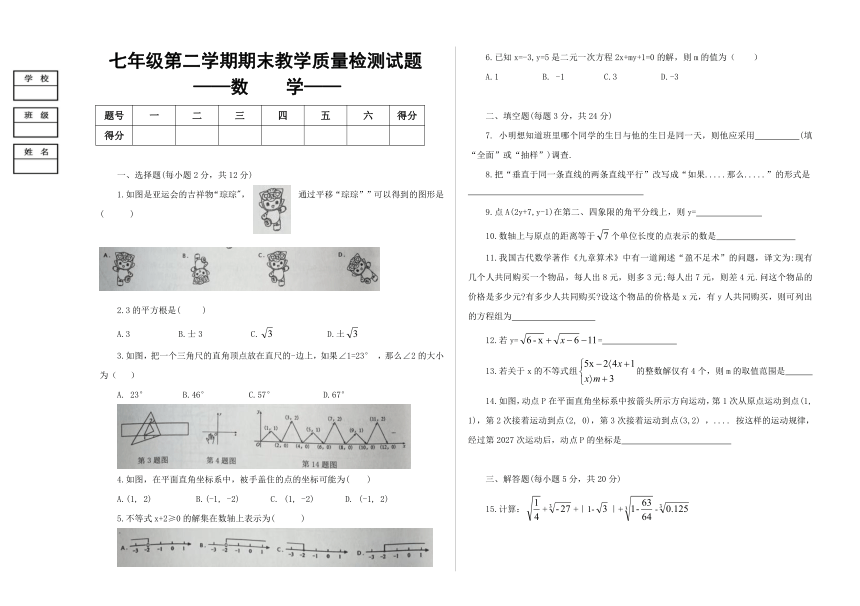
1.如图是亚运会的吉祥物“琮琮",通过平移“琮琮””可以得到的图形是( )
2.3的平方根是( )
A.3 B.士3 C. D.土
3.如图,把一个三角尺的直角顶点放在直尺的-边上,如果∠1=23° ,那么∠2的大小为( )
A. 23° B.46° C.57° D.67°
4.如图,在平面直角坐标系中,被手盖住的点的坐标可能为( )
A.(1, 2) B.(-1, -2) C. (1, -2) D. (-1, 2)
5.不等式x+2≥0的解集在数轴上表示为( )
6.已知x=-3,y=5是二元一次方程2x+my+1=0的解,则m的值为( )
A.1 B. -1 C.3 D.-3
二、填空题(每题3分,共24分)
7. 小明想知道班里哪个同学的生日与他的生日是同一天,则他应采用 (填“全面”或“抽样”)调查.
8.把“垂直于同一条直线的两条直线平行”改写成“如果.....那么.....”的形式是
9.点A(2y+7,y-1)在第二、四象限的角平分线上,则y=
10.数轴上与原点的距离等于个单位长度的点表示的数是
11.我国古代数学著作《九章算术》中有一道阐述“盈不足术”的问题,译文为:现有几个人共同购买一个物品,每人出8元,则多3元;每人出7元,则差4元.问这个物品的价格是多少元 有多少人共同购买 设这个物品的价格是x元,有y人共同购买,则可列出的方程组为
12.若y==
13.若关于x的不等式组的整数解仅有4个,则m的取值范围是
14.如图,动点P在平面直角坐标系中按箭头所示方向运动,第1次从原点运动到点(1, 1),第2次接着运动到点(2, 0),第3次接着运动到点(3,2) ,.... 按这样的运动规律,经过第2027次运动后,动点P的坐标是
三、解答题(每小题5分,共20分)
15.计算:++|1-|+-
16.解不等式组并把解集在数轴上表示出来.
17.解方程组
18.如图,直线EF分别与直线AB,CD交于点E,F. EM平分∠BEF, FN平分∠CFE,且EM// FN.
求证: AB//CD
四、解答题 (每小题7分, 共28分)
19.一艘轮船在相距120千米的甲、乙两地之间匀速航行,从甲地到乙地顺流航行用了6小时,逆流航行比顺流航行多用了4小时.求该轮船在静水中的速度和水流速度.
20.完成下面的证明.
如图,DG⊥BC, AC⊥BC,EF⊥AB, ∠1=∠2,求证: CD⊥AB.
证明: ∵ DG⊥BC, AC⊥BC (已知),
∴ ∠DGB=∠ACB=90° (垂直的定义) ,
∴ DG//AC ( ),
∴ ∠2=∠ ( )
∵ ∠1=∠2 (已知)
∴ ∠1= (等量代换),
∴ EF//CD( ),
∴ ∠AEF=∠ADC ( ) ,
∵ EF⊥AB(已知)
∴ ∠AEF=90° (垂直的定义 ),
∴ ∠ADC=90° ( ),
∴ CD⊥AB.
21.已知2a -7的平方根是士3, 2a+b- 1的算术平方根是4,求a+b- 1的立方根.
22.如图,在平面直角坐标系中,△ABC的顶点都在网格格点上,其中点C的坐标为(1,2)
(1)点A的坐标是 ,点B的坐标是
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A'B'C'.请在图中画出△A'B'C',并写出它的三个顶点的坐标.
(3)求△A'B'C'的面积.
五、解答题(每小题8分,共16分)
23.某校计划开设美术、书法、音乐、体育兴趣班,为了解学生报名意向,随机调查了部分学生,要求被调查的学生必选且只选项,根据调查结果绘制出如下不完整的统计图表:
根据统计图表的信息,解答下列问题:
(1)直接写出本次调查的样本容量和表中a,b, C的值.
(2)将折线图补充完整.
(3)该校现有3000名学生,估计该校参加音乐兴趣班的学生有多少人
24.如图,AE//CF,ZA=ZC.
(1)∠1=35°,求∠2的度数.
(2)判断BC与AD的位置关系,并说明理由.
(3)若DA平分∠BDF,求证: BC平分∠DBE.
六、解答题(每小题10分,共20分)
25.某市政府部门招标工程队负责在山脚下修建一座水库的土方施 工任务.该工程队有A、B两种型号的挖掘机,已知3台A型和5台B型挖掘机同时施工一小时挖 土165立方米;4台A型和7台B型挖掘机同时施工一小时挖 士225立方米.每台A型挖掘机小时的施工费用为300元,每台B型挖掘机小时的施工费用为180元.
(1)分别求每台A型,B型挖掘机小时挖土多少立方米
(2)若不同数量的A型,B型挖掘机共12台同时施工4小时,至少完成1080立方米的挖土量,且总费用不超过12960元.问施工时有哪几种调配方案,并指出哪种调配方案的施工费用最低,最低费用是多少元
26.如图,在平面直角坐标系中,长方形OABC的边0C、OA 分别在x轴、y轴上,B点在第一象限,点A的坐标是(0,4) ,0C=8.
(1)直接写出点B、点C的坐标.
(2)点P从原点0出发,在边OC上以每秒1个单位长度的速度匀速向C点运动,同时点Q从点B出发,在边BA上以每秒2个单位长度的速度匀速向A点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t秒,探究下列问题:
①当t为多少时,直线PQ//y轴
②在运动过程中,当点Q到y轴的距离为2个单位长度时,求t的值.
③在整个运动过程中,能否使得四边形BCPQ的面积是长方形0ABC面积的?若能,请求出P、Q两点的坐标;若不能,说明理由.
七年级第二学期期末教学质量检测
数学参考答案
一、选择题
1.C 2.D 3.D 4.B 5.D 6.A
二、填空题
7.全面
8.如果两条直线都垂直于同一条直线,那么这两直线互相平行
9.-2
10.
11.
12.-5
13.
14.(2027,2)
三、解答题
15.解:原式=
16.解:
解不等式①,得x>-2
解不等式②,得x≤1
∴原不等式组的解集为-2解:原方程组的解为
证明:∵EM平分∠BEF
∴∠MEF=∠BEF
∵FN平分∠CFE
∴∠NFE=∠CFE
∵EM//FN
∴∠MEF=∠NFE
∴∠BEF=∠CFE
∴ AB//CD
四、解答题
19.解:设该轮船在静水中的速度为,水流速度为.
依题意,得 解得
答:该轮船在静水中的速度为,水流速度为.
同位角相等两直线平行
∠DCA 两直线平行,内错角相等
∠ACD
同位角相等,两直线平行
两直线平行,同位角相等
等量代换
21.解:∵的平方根是 ∴ ∴
∵的算术平方根是4 ∴
∴
∴ ∴的立方根为2
22.(1)点A的坐标是 (2,-1) ,点B的坐标是 (4,3) ;
(2)如图
(3).
五、解答题
23.解:(1)样本容量是100,a=30%,b=40,c=20%
(2)图略
(3)3000×20%=600(人)
答:估计该校参加音乐兴趣班的学生有600人。
24.解:(1)∵AE∥CF
∴∠DBE=∠2
∵∠1=35°∴∠DBE=180°-∠1=180°-35°=145°
BC∥AD
理由:∵AE∥CF
∴∠A+∠ADC=180°
∵∠A=∠C
∴∠C+∠ADC=180°
∴BC∥AD
证明:∵AE∥CF ∴∠DBE=∠BDF
∵BC∥AD ∴∠DBC=∠ADB
∵AD平分∠BDF
∴∠ADB=∠BDF
∴∠DBC=∠DBE
∴AD平分∠BDF
25.解:(1)设每台A型,B型挖掘机一小时分别挖土x立方米和y立方米,由题意,得解得
答:每台A型挖掘机一小时挖土30立方米,每台B型挖掘机一小时挖土15立方米。
(2)设每台A型挖掘机有台,则B型挖掘机有台,由题意,得
总费用为4×300+4×180=480+8640
∴解得
∵≠12-∴ ∴
∴共有三种调配方案:
方案一:A型挖掘机7台,B型挖掘机5台,总费用为4×7×300+4×5×180=12000(元)
方案二:A型挖掘机8台,B型挖掘机4台,总费用为4×8×300+4×4×180=12480(元)
方案三:A型挖掘机9台,B型挖掘机3台,总费用为4×9×300+4×3×180=12960(元)
∵12000<12480<12960
∴当A型挖掘机7台,B型挖掘机5台时,施工费用最低,最低费用为12000元.
26.解:(1)点B(8,4),点C(8,0)
(2)①∵PQ∥y轴
∴OP=AQ
∴t=8-2t 解得t=
②∵点Q到y轴的距离为2个单位长度
∴AQ=2
∴8-2t=2
∴t=3
③∵=8×4=32
∴2t+16=32×
∴t=2
∴点P的坐标是(2,0)点Q的坐标是(4,4)
——数 学——
题号 一 二 三 四 五 六 得分
得分
一、选择题(每小题2分,共12分)
1.如图是亚运会的吉祥物“琮琮",通过平移“琮琮””可以得到的图形是( )
2.3的平方根是( )
A.3 B.士3 C. D.土
3.如图,把一个三角尺的直角顶点放在直尺的-边上,如果∠1=23° ,那么∠2的大小为( )
A. 23° B.46° C.57° D.67°
4.如图,在平面直角坐标系中,被手盖住的点的坐标可能为( )
A.(1, 2) B.(-1, -2) C. (1, -2) D. (-1, 2)
5.不等式x+2≥0的解集在数轴上表示为( )
6.已知x=-3,y=5是二元一次方程2x+my+1=0的解,则m的值为( )
A.1 B. -1 C.3 D.-3
二、填空题(每题3分,共24分)
7. 小明想知道班里哪个同学的生日与他的生日是同一天,则他应采用 (填“全面”或“抽样”)调查.
8.把“垂直于同一条直线的两条直线平行”改写成“如果.....那么.....”的形式是
9.点A(2y+7,y-1)在第二、四象限的角平分线上,则y=
10.数轴上与原点的距离等于个单位长度的点表示的数是
11.我国古代数学著作《九章算术》中有一道阐述“盈不足术”的问题,译文为:现有几个人共同购买一个物品,每人出8元,则多3元;每人出7元,则差4元.问这个物品的价格是多少元 有多少人共同购买 设这个物品的价格是x元,有y人共同购买,则可列出的方程组为
12.若y==
13.若关于x的不等式组的整数解仅有4个,则m的取值范围是
14.如图,动点P在平面直角坐标系中按箭头所示方向运动,第1次从原点运动到点(1, 1),第2次接着运动到点(2, 0),第3次接着运动到点(3,2) ,.... 按这样的运动规律,经过第2027次运动后,动点P的坐标是
三、解答题(每小题5分,共20分)
15.计算:++|1-|+-
16.解不等式组并把解集在数轴上表示出来.
17.解方程组
18.如图,直线EF分别与直线AB,CD交于点E,F. EM平分∠BEF, FN平分∠CFE,且EM// FN.
求证: AB//CD
四、解答题 (每小题7分, 共28分)
19.一艘轮船在相距120千米的甲、乙两地之间匀速航行,从甲地到乙地顺流航行用了6小时,逆流航行比顺流航行多用了4小时.求该轮船在静水中的速度和水流速度.
20.完成下面的证明.
如图,DG⊥BC, AC⊥BC,EF⊥AB, ∠1=∠2,求证: CD⊥AB.
证明: ∵ DG⊥BC, AC⊥BC (已知),
∴ ∠DGB=∠ACB=90° (垂直的定义) ,
∴ DG//AC ( ),
∴ ∠2=∠ ( )
∵ ∠1=∠2 (已知)
∴ ∠1= (等量代换),
∴ EF//CD( ),
∴ ∠AEF=∠ADC ( ) ,
∵ EF⊥AB(已知)
∴ ∠AEF=90° (垂直的定义 ),
∴ ∠ADC=90° ( ),
∴ CD⊥AB.
21.已知2a -7的平方根是士3, 2a+b- 1的算术平方根是4,求a+b- 1的立方根.
22.如图,在平面直角坐标系中,△ABC的顶点都在网格格点上,其中点C的坐标为(1,2)
(1)点A的坐标是 ,点B的坐标是
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A'B'C'.请在图中画出△A'B'C',并写出它的三个顶点的坐标.
(3)求△A'B'C'的面积.
五、解答题(每小题8分,共16分)
23.某校计划开设美术、书法、音乐、体育兴趣班,为了解学生报名意向,随机调查了部分学生,要求被调查的学生必选且只选项,根据调查结果绘制出如下不完整的统计图表:
根据统计图表的信息,解答下列问题:
(1)直接写出本次调查的样本容量和表中a,b, C的值.
(2)将折线图补充完整.
(3)该校现有3000名学生,估计该校参加音乐兴趣班的学生有多少人
24.如图,AE//CF,ZA=ZC.
(1)∠1=35°,求∠2的度数.
(2)判断BC与AD的位置关系,并说明理由.
(3)若DA平分∠BDF,求证: BC平分∠DBE.
六、解答题(每小题10分,共20分)
25.某市政府部门招标工程队负责在山脚下修建一座水库的土方施 工任务.该工程队有A、B两种型号的挖掘机,已知3台A型和5台B型挖掘机同时施工一小时挖 土165立方米;4台A型和7台B型挖掘机同时施工一小时挖 士225立方米.每台A型挖掘机小时的施工费用为300元,每台B型挖掘机小时的施工费用为180元.
(1)分别求每台A型,B型挖掘机小时挖土多少立方米
(2)若不同数量的A型,B型挖掘机共12台同时施工4小时,至少完成1080立方米的挖土量,且总费用不超过12960元.问施工时有哪几种调配方案,并指出哪种调配方案的施工费用最低,最低费用是多少元
26.如图,在平面直角坐标系中,长方形OABC的边0C、OA 分别在x轴、y轴上,B点在第一象限,点A的坐标是(0,4) ,0C=8.
(1)直接写出点B、点C的坐标.
(2)点P从原点0出发,在边OC上以每秒1个单位长度的速度匀速向C点运动,同时点Q从点B出发,在边BA上以每秒2个单位长度的速度匀速向A点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t秒,探究下列问题:
①当t为多少时,直线PQ//y轴
②在运动过程中,当点Q到y轴的距离为2个单位长度时,求t的值.
③在整个运动过程中,能否使得四边形BCPQ的面积是长方形0ABC面积的?若能,请求出P、Q两点的坐标;若不能,说明理由.
七年级第二学期期末教学质量检测
数学参考答案
一、选择题
1.C 2.D 3.D 4.B 5.D 6.A
二、填空题
7.全面
8.如果两条直线都垂直于同一条直线,那么这两直线互相平行
9.-2
10.
11.
12.-5
13.
14.(2027,2)
三、解答题
15.解:原式=
16.解:
解不等式①,得x>-2
解不等式②,得x≤1
∴原不等式组的解集为-2
证明:∵EM平分∠BEF
∴∠MEF=∠BEF
∵FN平分∠CFE
∴∠NFE=∠CFE
∵EM//FN
∴∠MEF=∠NFE
∴∠BEF=∠CFE
∴ AB//CD
四、解答题
19.解:设该轮船在静水中的速度为,水流速度为.
依题意,得 解得
答:该轮船在静水中的速度为,水流速度为.
同位角相等两直线平行
∠DCA 两直线平行,内错角相等
∠ACD
同位角相等,两直线平行
两直线平行,同位角相等
等量代换
21.解:∵的平方根是 ∴ ∴
∵的算术平方根是4 ∴
∴
∴ ∴的立方根为2
22.(1)点A的坐标是 (2,-1) ,点B的坐标是 (4,3) ;
(2)如图
(3).
五、解答题
23.解:(1)样本容量是100,a=30%,b=40,c=20%
(2)图略
(3)3000×20%=600(人)
答:估计该校参加音乐兴趣班的学生有600人。
24.解:(1)∵AE∥CF
∴∠DBE=∠2
∵∠1=35°∴∠DBE=180°-∠1=180°-35°=145°
BC∥AD
理由:∵AE∥CF
∴∠A+∠ADC=180°
∵∠A=∠C
∴∠C+∠ADC=180°
∴BC∥AD
证明:∵AE∥CF ∴∠DBE=∠BDF
∵BC∥AD ∴∠DBC=∠ADB
∵AD平分∠BDF
∴∠ADB=∠BDF
∴∠DBC=∠DBE
∴AD平分∠BDF
25.解:(1)设每台A型,B型挖掘机一小时分别挖土x立方米和y立方米,由题意,得解得
答:每台A型挖掘机一小时挖土30立方米,每台B型挖掘机一小时挖土15立方米。
(2)设每台A型挖掘机有台,则B型挖掘机有台,由题意,得
总费用为4×300+4×180=480+8640
∴解得
∵≠12-∴ ∴
∴共有三种调配方案:
方案一:A型挖掘机7台,B型挖掘机5台,总费用为4×7×300+4×5×180=12000(元)
方案二:A型挖掘机8台,B型挖掘机4台,总费用为4×8×300+4×4×180=12480(元)
方案三:A型挖掘机9台,B型挖掘机3台,总费用为4×9×300+4×3×180=12960(元)
∵12000<12480<12960
∴当A型挖掘机7台,B型挖掘机5台时,施工费用最低,最低费用为12000元.
26.解:(1)点B(8,4),点C(8,0)
(2)①∵PQ∥y轴
∴OP=AQ
∴t=8-2t 解得t=
②∵点Q到y轴的距离为2个单位长度
∴AQ=2
∴8-2t=2
∴t=3
③∵=8×4=32
∴2t+16=32×
∴t=2
∴点P的坐标是(2,0)点Q的坐标是(4,4)
同课章节目录
