2.3匀变速直线运动的位移与时间的关系 课件(共35张ppt)物理人教版(2019)必修第一册
文档属性
| 名称 | 2.3匀变速直线运动的位移与时间的关系 课件(共35张ppt)物理人教版(2019)必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-07-10 12:30:12 | ||
图片预览









文档简介
(共35张PPT)
第二章 匀变速直线运动的研究
2.3 匀变速直线运动的位移与时间的关系
目录
01
位移与时间的关系
02
速度与位移的关系
03
位移-时间图像
一、位移与时间的关系
v/m.s-1
3
2
1
0
1
2
3
4
t/s
5
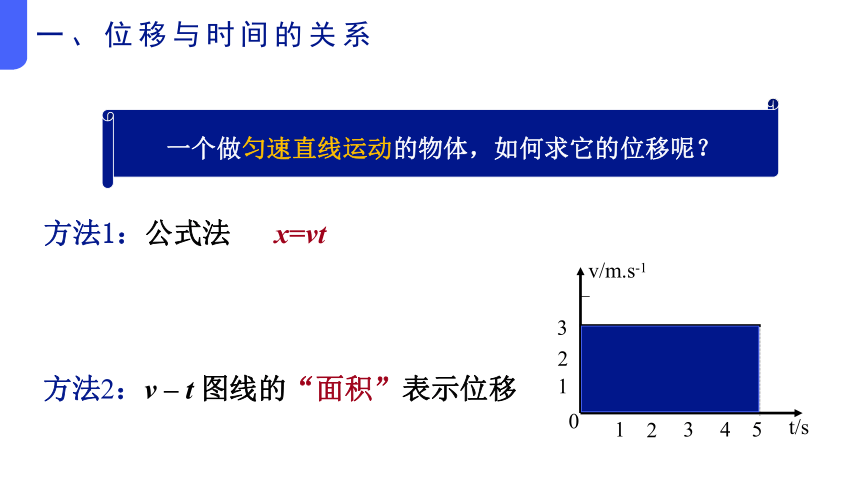
方法1:公式法 x=vt
方法2:v – t 图线的“面积”表示位移
一个做匀速直线运动的物体,如何求它的位移呢?
v/m·s-1
t/s
2
6
4
10
8
3
4
5
0
2
1
-2
-4
1、位移是矢量,有正有负,该如何用面积表示?
2、8s内位移是多少?如何用图像求解?
7
8
9
6
面积正负的含义:
(1)t轴上方面积为正,表示位移为正方向
(2)t轴下方面积为负,表示位移为负方向
一、位移与时间的关系
一、位移与时间的关系
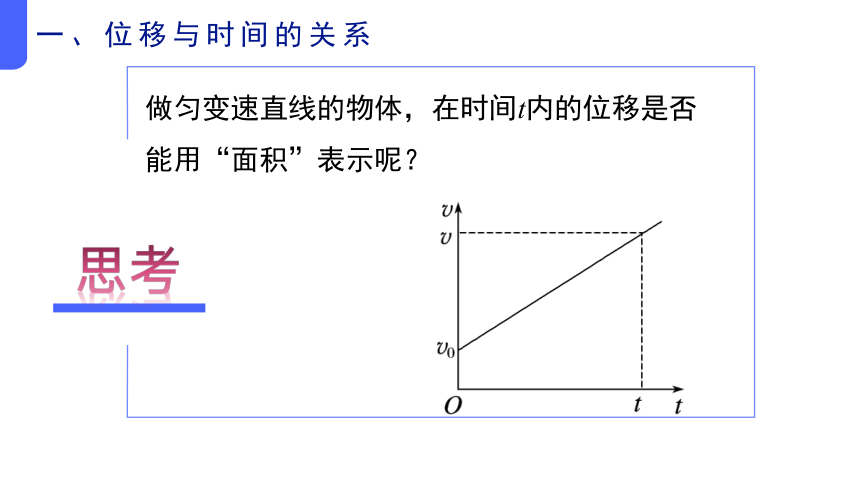
做匀变速直线的物体,在时间t内的位移是否能用“面积”表示呢?
思考
一、位移与时间的关系
把物体的运动分成5段,每一段时间内,看成匀速直线运动
如果把过程分割为更多的小段,和甲图相比,哪种情形更接近整个过程的位移?
依次类推,如果把过程分割成无数个小段,用梯形的面积代表物体在这段时间的位移
一、位移与时间的关系
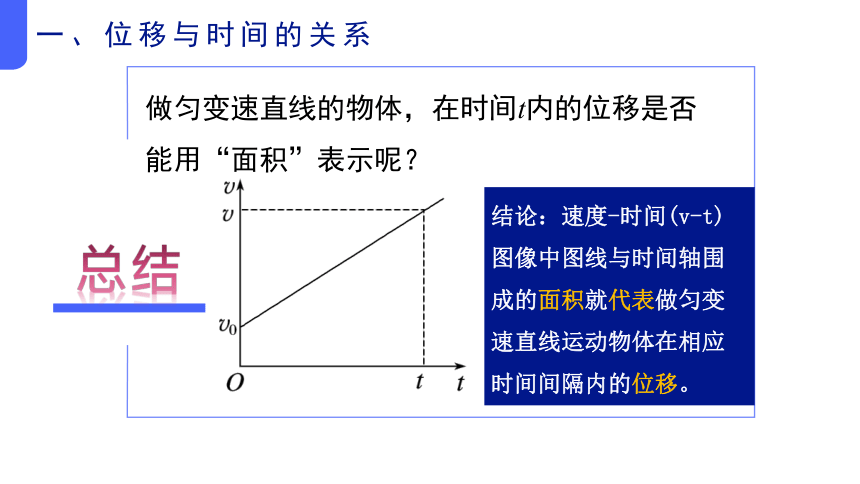
做匀变速直线的物体,在时间t内的位移是否能用“面积”表示呢?
总结
结论:速度-时间(v-t)图像中图线与时间轴围成的面积就代表做匀变速直线运动物体在相应时间间隔内的位移。
v
O
t
t
O
v
v0
t
t
2t
v
O
t
t
2t
思考与讨论
v
O
t
t
O
v
t
t
-v0
推导:由图可知梯形的面积:
即得位移:
将v=v0+at代入上式得:
一、位移与时间的关系
1.公式:
2.适用条件:只适用于匀变速直线运动。
3.矢量式:υ0、α、x均为矢量,使用公式时应先规定正方向。
(一般以υ0的方向为正方向)
一、位移与时间的关系
4.公式的特殊形式:
(1)当a=0时:
(2)当v0=0时:
(由静止开始的匀加速直线运动)。
(匀速直线运动)。
一、位移与时间的关系
逆向思维法:末速度为0的匀减速直线运动可视为反方向的初 速度为0的匀加速直线运动。
【例1】以36 km/h的速度行驶的列车开始下坡,在下坡路上的加速度等于0.2 m/s2,经过30 s到达坡底,求坡路的长度和列车到达坡底时的速度大小。
解:设坡路的长度为x,列车到达坡底时的速度大小为v,
初速度v0=36 km/h=10 m/s,
加速度a=0.2 m/s2,时间t=30 s,
根据v=v0+at,
得v=10 m/s+0.2 m/s2×30 s=16 m/s。
一、位移与时间的关系
【例2】以20m/s速度竖直上抛小球,加速度向下,大小为10m/s2,求1 s, 3 s, 5 s时小球的位移。
解:1 s, 3 s, 5 s时小球的位移分别为x1, x2, x3
根据匀变速直线运动的位移与时间的关系式得:
1 s, 3 s, 5 s时小球的位移分别为15m, 15m和-25m
一、位移与时间的关系
【例2拓展】
(1)位移为15m时物体运动的时间?
(2)位移为-25m时物体运动的时间?
(3)位移为25m时物体运动的时间?
t=1s;t=3s
t=5s;t=-1s(舍)
Δ<0,无实根
一、位移与时间的关系
一、位移与时间的关系
注意
①:公式中的x是位移不是路程
②:不能通过位移x正负判断速度v方向
③:注意时间t的物理意义,不能存在负数
思考与讨论
a不变
v=v0+at
?
时间
位移
速度
速度时间关系
位移时间关系
速度位移关系
速度公式:
位移公式:
二、速度与位移的关系
化简得:
代入
1.公式:
2.适用条件:只适用于匀变速直线运动
当v0=0时:
3.矢量式:v、υ0、α、x均为矢量,使用公式时应先规定正方向。 (一般以υ0的方向为正方向)
4.公式的特殊形式:
注:(1)物体做加速运动时,a取正值,做减速运动时,a取负值。
(2)x>0,说明物体通过的位移方向与初速度方向相同;x<0,说明位移的方向与初速度的方向相反。
二、速度与位移的关系
【例题3】某型号航空母舰上装有帮助飞机起飞的弹射系统,已知某型号的飞机在平直跑道上加速时可产生的最大加速度为5.0 m/s2,当飞机的速度达到50 m/s时才能离开航空母舰起飞,设航空母舰始终处于静止状态。问:
(1)若某舰上不装弹射系统,要求该型号飞机仍能在此舰上正常起飞,该舰身至少为多长?
(2)若要求该飞机滑行160 m后起飞,弹射系统必须使飞机具有多大的初速度?
二、速度与位移的关系
解:(1)不装弹射系统时,飞机从静止开始做匀加速直线运动, 由公式v2=2ax可知
该舰身长至少为x1= =250 m。
(2)设弹射系统使飞机具有的初速度为v0,
由速度与位移的关系式v2-v02=2ax
二、速度与位移的关系
【例题4】一汽车在水平路面上匀速行驶,速度v0=10 m/s,突然前方出现紧急情况,司机以5 m/s2的加速度刹车,求汽车开始刹车后1 s内和3 s内的位移。
解:首先根据v=v0+at0
因t2=3 s>t0
二、速度与位移的关系
刹车类问题的分析思路:
注意
(1)如果t0(2)如果t0>t,说明经过时间t运动还没有停止,则应用题目所给的时间t直接求解位移。
二、速度与位移的关系
三、位移—时间图像
0
t1
x1
A
t/s
x/m
x2
B
图像的斜率表示速度,斜率越大的速度越大。
斜率KA=x1/t1
斜率KB=x2/t1
x/m
0
t/s
斜率为0,表示物体静止。
三、位移—时间图像
30
20
10
0
x/m
1
2
3
①
②
①图象与x轴(纵轴)交点:
表示物体出发时的位置坐标 x=30m。
②图象与t轴(横轴)交点:
表示物体在t=1s时才开始出发。
③ x-t 图象中,两个图线的“交点”表示:
两物体在该( t=2s)时刻相遇。
x-t 图象—图线的交点
t/s
三、位移—时间图像
x/m
t/s
1
2
3
A
B
思考:A、B运动轨迹是曲线?
x-t 图象描述物体的位移随时间的变化规律,并不是物体运动的轨迹。
A质点速度越来越小
B质点速度越来越大
总结
三、位移—时间图像
物理意义:
描述物体位移随时间的变化关系
1、图线上任意一点的横纵坐标表示物体在某一时刻及所处的位置。
2、图线上起点的横纵坐标表示物体开始运动的时刻及位置。
3、x-t图像表示的是位移随时间变化的情况,不是运动的轨迹。
4、x-t图像只能表示直线运动,不能描述曲线运动。
5、x-t图像的斜率表示速度,图线倾斜程度(斜率)越大,速度越大。
其他非常规图像
图像种类 示例 解题关键
公式依据:
斜率意义:初速度v0
纵截距意义:
加速度的一半
a-x图像
公式依据:t=
面积意义:运动时间t
课堂小结
1.匀变速直线运动位移与时间的关系式:x=_________
当v0=0时,x=_____(由静止开始的匀加速直线运动),此时x∝t2。
2.适用范围:仅适用于_______直线运动。
3.公式的矢量性:公式中x、v0、a都是_____,应用时必须选取正方向。
4.匀变速直线运动速度与位移的关系式:_______=2ax。
适用范围:仅适用于___________运动。
5.位移-时间图像的斜率表示速度,斜率越大的速度越大。
匀变速
矢量
v2-v02
匀变速直线
课堂练习
1.某质点的位移随时间变化的关系式为x=4t+2t2,x与t的单位分别是m和s,则质点的初速度和加速度分别是( )
A.4m/s和2 m/s2
B.0和4m/s2
C.4m/s 和4 m/s2
D.4m/s和0
C
课堂练习
2.一质点做初速度为2 m/s,加速度为4 m/s2的匀加速直线运动,在0~2 s内质点的位移大小为
A.10 m B.12 m C.14 m D.16 m
B
课堂练习
3.
某质点从静止开始做匀加速直线运动,已知第1 s内通过的位移是2 m,则质点运动的加速度为
A.2 m/s B.2 m/s2 C.4 m/s D.4 m/s2
D
课堂练习
D
4.某汽车沿直线刹车时的位移x与时间t的关系式为x=12t-2t2,式中位移x的单位是m,时间t的单位是s,则该汽车在刹车过程中
A.加速度大小是2 m/s2
B.初速度是2 m/s
C.任意1 s内的速度变化量都是2 m/s
D.前4 s内的位移大小是18 m
5、从t=0时刻开始,物块在外力作用下沿x轴从原点出发,做匀变速直线运动,如图所示为其v-t图像,下列说法正确的是( )
A.物块的初速度v0=0
B.物块运动的加速度a=7.5m/s2
C.t=2s时,物块位于x=20m处
D.物块在前4s内的位移大小为x=80m
D
课堂练习
THANKS
感谢观看
THANKS
第二章 匀变速直线运动的研究
2.3 匀变速直线运动的位移与时间的关系
目录
01
位移与时间的关系
02
速度与位移的关系
03
位移-时间图像
一、位移与时间的关系
v/m.s-1
3
2
1
0
1
2
3
4
t/s
5
方法1:公式法 x=vt
方法2:v – t 图线的“面积”表示位移
一个做匀速直线运动的物体,如何求它的位移呢?
v/m·s-1
t/s
2
6
4
10
8
3
4
5
0
2
1
-2
-4
1、位移是矢量,有正有负,该如何用面积表示?
2、8s内位移是多少?如何用图像求解?
7
8
9
6
面积正负的含义:
(1)t轴上方面积为正,表示位移为正方向
(2)t轴下方面积为负,表示位移为负方向
一、位移与时间的关系
一、位移与时间的关系
做匀变速直线的物体,在时间t内的位移是否能用“面积”表示呢?
思考
一、位移与时间的关系
把物体的运动分成5段,每一段时间内,看成匀速直线运动
如果把过程分割为更多的小段,和甲图相比,哪种情形更接近整个过程的位移?
依次类推,如果把过程分割成无数个小段,用梯形的面积代表物体在这段时间的位移
一、位移与时间的关系
做匀变速直线的物体,在时间t内的位移是否能用“面积”表示呢?
总结
结论:速度-时间(v-t)图像中图线与时间轴围成的面积就代表做匀变速直线运动物体在相应时间间隔内的位移。
v
O
t
t
O
v
v0
t
t
2t
v
O
t
t
2t
思考与讨论
v
O
t
t
O
v
t
t
-v0
推导:由图可知梯形的面积:
即得位移:
将v=v0+at代入上式得:
一、位移与时间的关系
1.公式:
2.适用条件:只适用于匀变速直线运动。
3.矢量式:υ0、α、x均为矢量,使用公式时应先规定正方向。
(一般以υ0的方向为正方向)
一、位移与时间的关系
4.公式的特殊形式:
(1)当a=0时:
(2)当v0=0时:
(由静止开始的匀加速直线运动)。
(匀速直线运动)。
一、位移与时间的关系
逆向思维法:末速度为0的匀减速直线运动可视为反方向的初 速度为0的匀加速直线运动。
【例1】以36 km/h的速度行驶的列车开始下坡,在下坡路上的加速度等于0.2 m/s2,经过30 s到达坡底,求坡路的长度和列车到达坡底时的速度大小。
解:设坡路的长度为x,列车到达坡底时的速度大小为v,
初速度v0=36 km/h=10 m/s,
加速度a=0.2 m/s2,时间t=30 s,
根据v=v0+at,
得v=10 m/s+0.2 m/s2×30 s=16 m/s。
一、位移与时间的关系
【例2】以20m/s速度竖直上抛小球,加速度向下,大小为10m/s2,求1 s, 3 s, 5 s时小球的位移。
解:1 s, 3 s, 5 s时小球的位移分别为x1, x2, x3
根据匀变速直线运动的位移与时间的关系式得:
1 s, 3 s, 5 s时小球的位移分别为15m, 15m和-25m
一、位移与时间的关系
【例2拓展】
(1)位移为15m时物体运动的时间?
(2)位移为-25m时物体运动的时间?
(3)位移为25m时物体运动的时间?
t=1s;t=3s
t=5s;t=-1s(舍)
Δ<0,无实根
一、位移与时间的关系
一、位移与时间的关系
注意
①:公式中的x是位移不是路程
②:不能通过位移x正负判断速度v方向
③:注意时间t的物理意义,不能存在负数
思考与讨论
a不变
v=v0+at
?
时间
位移
速度
速度时间关系
位移时间关系
速度位移关系
速度公式:
位移公式:
二、速度与位移的关系
化简得:
代入
1.公式:
2.适用条件:只适用于匀变速直线运动
当v0=0时:
3.矢量式:v、υ0、α、x均为矢量,使用公式时应先规定正方向。 (一般以υ0的方向为正方向)
4.公式的特殊形式:
注:(1)物体做加速运动时,a取正值,做减速运动时,a取负值。
(2)x>0,说明物体通过的位移方向与初速度方向相同;x<0,说明位移的方向与初速度的方向相反。
二、速度与位移的关系
【例题3】某型号航空母舰上装有帮助飞机起飞的弹射系统,已知某型号的飞机在平直跑道上加速时可产生的最大加速度为5.0 m/s2,当飞机的速度达到50 m/s时才能离开航空母舰起飞,设航空母舰始终处于静止状态。问:
(1)若某舰上不装弹射系统,要求该型号飞机仍能在此舰上正常起飞,该舰身至少为多长?
(2)若要求该飞机滑行160 m后起飞,弹射系统必须使飞机具有多大的初速度?
二、速度与位移的关系
解:(1)不装弹射系统时,飞机从静止开始做匀加速直线运动, 由公式v2=2ax可知
该舰身长至少为x1= =250 m。
(2)设弹射系统使飞机具有的初速度为v0,
由速度与位移的关系式v2-v02=2ax
二、速度与位移的关系
【例题4】一汽车在水平路面上匀速行驶,速度v0=10 m/s,突然前方出现紧急情况,司机以5 m/s2的加速度刹车,求汽车开始刹车后1 s内和3 s内的位移。
解:首先根据v=v0+at0
因t2=3 s>t0
二、速度与位移的关系
刹车类问题的分析思路:
注意
(1)如果t0
二、速度与位移的关系
三、位移—时间图像
0
t1
x1
A
t/s
x/m
x2
B
图像的斜率表示速度,斜率越大的速度越大。
斜率KA=x1/t1
斜率KB=x2/t1
x/m
0
t/s
斜率为0,表示物体静止。
三、位移—时间图像
30
20
10
0
x/m
1
2
3
①
②
①图象与x轴(纵轴)交点:
表示物体出发时的位置坐标 x=30m。
②图象与t轴(横轴)交点:
表示物体在t=1s时才开始出发。
③ x-t 图象中,两个图线的“交点”表示:
两物体在该( t=2s)时刻相遇。
x-t 图象—图线的交点
t/s
三、位移—时间图像
x/m
t/s
1
2
3
A
B
思考:A、B运动轨迹是曲线?
x-t 图象描述物体的位移随时间的变化规律,并不是物体运动的轨迹。
A质点速度越来越小
B质点速度越来越大
总结
三、位移—时间图像
物理意义:
描述物体位移随时间的变化关系
1、图线上任意一点的横纵坐标表示物体在某一时刻及所处的位置。
2、图线上起点的横纵坐标表示物体开始运动的时刻及位置。
3、x-t图像表示的是位移随时间变化的情况,不是运动的轨迹。
4、x-t图像只能表示直线运动,不能描述曲线运动。
5、x-t图像的斜率表示速度,图线倾斜程度(斜率)越大,速度越大。
其他非常规图像
图像种类 示例 解题关键
公式依据:
斜率意义:初速度v0
纵截距意义:
加速度的一半
a-x图像
公式依据:t=
面积意义:运动时间t
课堂小结
1.匀变速直线运动位移与时间的关系式:x=_________
当v0=0时,x=_____(由静止开始的匀加速直线运动),此时x∝t2。
2.适用范围:仅适用于_______直线运动。
3.公式的矢量性:公式中x、v0、a都是_____,应用时必须选取正方向。
4.匀变速直线运动速度与位移的关系式:_______=2ax。
适用范围:仅适用于___________运动。
5.位移-时间图像的斜率表示速度,斜率越大的速度越大。
匀变速
矢量
v2-v02
匀变速直线
课堂练习
1.某质点的位移随时间变化的关系式为x=4t+2t2,x与t的单位分别是m和s,则质点的初速度和加速度分别是( )
A.4m/s和2 m/s2
B.0和4m/s2
C.4m/s 和4 m/s2
D.4m/s和0
C
课堂练习
2.一质点做初速度为2 m/s,加速度为4 m/s2的匀加速直线运动,在0~2 s内质点的位移大小为
A.10 m B.12 m C.14 m D.16 m
B
课堂练习
3.
某质点从静止开始做匀加速直线运动,已知第1 s内通过的位移是2 m,则质点运动的加速度为
A.2 m/s B.2 m/s2 C.4 m/s D.4 m/s2
D
课堂练习
D
4.某汽车沿直线刹车时的位移x与时间t的关系式为x=12t-2t2,式中位移x的单位是m,时间t的单位是s,则该汽车在刹车过程中
A.加速度大小是2 m/s2
B.初速度是2 m/s
C.任意1 s内的速度变化量都是2 m/s
D.前4 s内的位移大小是18 m
5、从t=0时刻开始,物块在外力作用下沿x轴从原点出发,做匀变速直线运动,如图所示为其v-t图像,下列说法正确的是( )
A.物块的初速度v0=0
B.物块运动的加速度a=7.5m/s2
C.t=2s时,物块位于x=20m处
D.物块在前4s内的位移大小为x=80m
D
课堂练习
THANKS
感谢观看
THANKS
