【湘教版数学八年级上册同步练习】 2.5全等三角形(含答案)
文档属性
| 名称 | 【湘教版数学八年级上册同步练习】 2.5全等三角形(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-10 17:24:26 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【湘教版数学八年级上册同步练习】
2.5全等三角形
一、单选题
1.如图,点在同一直线上,,添加以下条件不能判定的是( )
A. B. C. D.
2.如图,在∠AOB的两边上,分别取OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP,则OP平分∠AOB的依据是( )
A.SSS B.SAS C.AAS D.HL
3.如图,直角三角形被挡住了一部分,小明根据所学知识很快就另外画出了一个与原来完全一样的三角形,这两个三角形全等的依据是( )
A.SAS B.ASA C.AAS D.HL
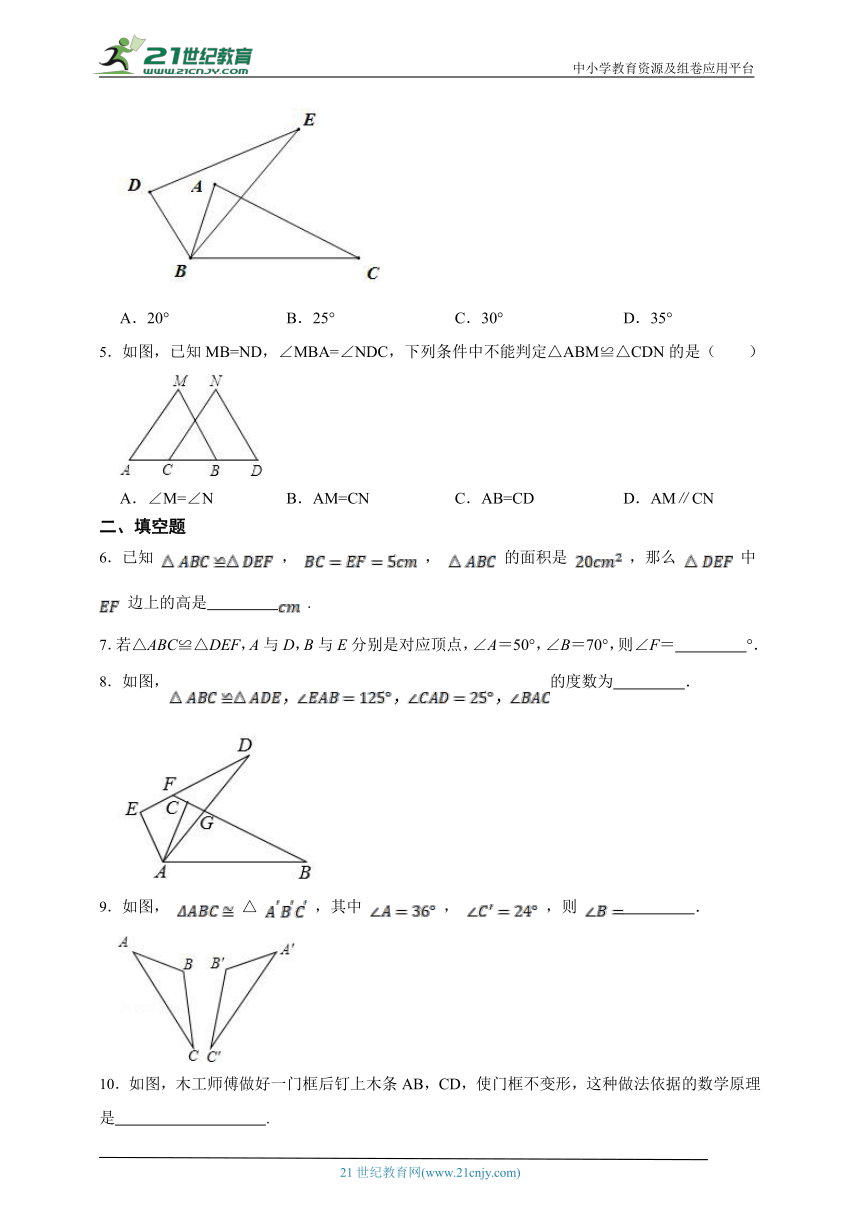
4.如图,,,,则的度数为( )
A.20° B.25° C.30° D.35°
5.如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )
A.∠M=∠N B.AM=CN C.AB=CD D.AM∥CN
二、填空题
6.已知 , , 的面积是 ,那么 中 边上的高是 .
7.若△ABC≌△DEF,A与D,B与E分别是对应顶点,∠A=50°,∠B=70°,则∠F= °.
8.如图,的度数为 .
9.如图, △ ,其中 , ,则 .
10.如图,木工师傅做好一门框后钉上木条AB,CD,使门框不变形,这种做法依据的数学原理是 .
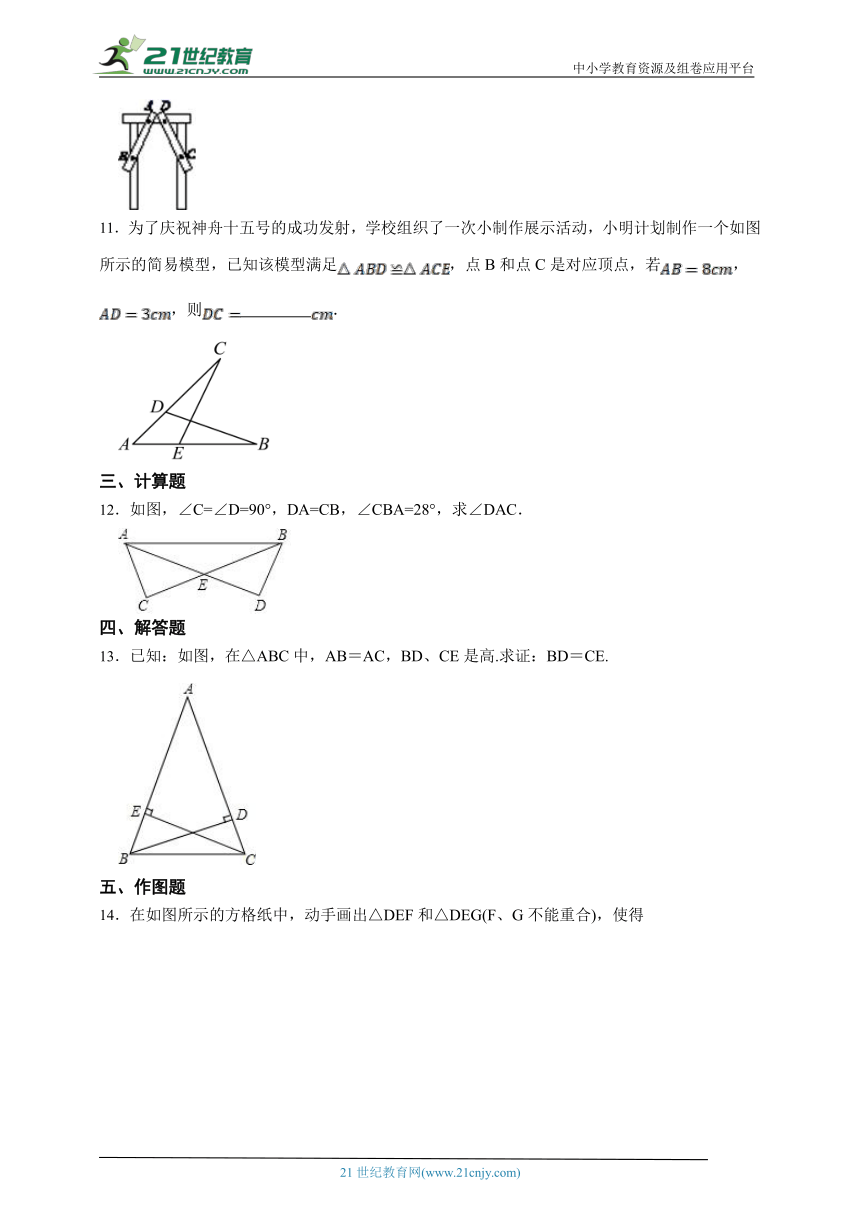
11.为了庆祝神舟十五号的成功发射,学校组织了一次小制作展示活动,小明计划制作一个如图所示的简易模型,已知该模型满足,点B和点C是对应顶点,若,,则 .
三、计算题
12.如图,∠C=∠D=90°,DA=CB,∠CBA=28°,求∠DAC.
四、解答题
13.已知:如图,在△ABC中,AB=AC,BD、CE是高.求证:BD=CE.
五、作图题
14.在如图所示的方格纸中,动手画出△DEF和△DEG(F、G不能重合),使得△ABC≌△DEF≌△DEG.(不用直尺画不得分)
六、综合题
15.已知:如图,已知 , , 和 相交于点 ,点 是 的中点,连接 .
(1)求证: ;
(2)求 的度数.
16.如图,点 B 为 AC 上一点,AD//CE,∠ADB = ∠CBE,BD = EB
求证:
(1)△ABD≌△CEB;
(2)AC = AD+ CE.
17.已知:如图,M是AB的中点,∠1=∠2,∠C=∠D,求证:
(1)△AMC≌△BMD;
(2)AC=BD.
答案解析部分
1.【答案】C
【知识点】三角形全等的判定
2.【答案】D
【知识点】三角形全等的判定
3.【答案】B
【知识点】三角形全等的判定-ASA
4.【答案】D
【知识点】三角形内角和定理;三角形全等及其性质
5.【答案】B
【知识点】三角形全等的判定
6.【答案】8
【知识点】三角形的面积;三角形全等及其性质
7.【答案】60
【知识点】三角形内角和定理;三角形全等及其性质
8.【答案】75°
【知识点】角的运算;三角形全等及其性质
9.【答案】
【知识点】三角形全等及其性质
10.【答案】三角形的稳定性
【知识点】三角形的稳定性
11.【答案】5
【知识点】三角形全等及其性质
12.【答案】解:在Rt△ABC和Rt△BAD中, ,
∴Rt△ABC≌Rt△BAD(HL),
∴∠DAB=∠CBA=28°,
∵∠C=90°,
∴∠BAC=90°﹣∠CBA=90°﹣28°=62°,
∴∠DAC=∠BAC﹣∠DAB=62°﹣28°=34°
【知识点】全等三角形的判定与性质
13.【答案】证明:∵BD、CE是高,
∴∠ADB=∠AEC=90°,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(AAS),
∴BD=CE.
【知识点】三角形全等的判定-AAS
14.【答案】解:
【知识点】三角形全等的判定
15.【答案】(1)证明:在 和 中,
,
∴
(2)解:∵ ,
∴ ,
∴ .
∵ 是 的中点,
∴ ,
∴
【知识点】等腰三角形的性质;三角形全等的判定-SSS
16.【答案】(1)证明:∵AD//CE,
∴∠A=∠C,
又∠ADB =
∠CBE,BD = EB
∴△ABD≌△CEB(AAS)
(2)证明:∵△ABD≌△CEB
∴AD=CB,AB=CE
∴AC
= AB+ BC= CE+AD,
即AC = AD+
CE
【知识点】全等三角形的判定与性质
17.【答案】(1)证明:∵点M是AB的中点,
∴AM=BM,
在△AMC和△BMD中,
,
∴△AMC≌△BMD(AAS)
(2)证明:∵△AMC≌△BMD,
∴AC=BD.
【知识点】三角形全等的判定-AAS
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【湘教版数学八年级上册同步练习】
2.5全等三角形
一、单选题
1.如图,点在同一直线上,,添加以下条件不能判定的是( )
A. B. C. D.
2.如图,在∠AOB的两边上,分别取OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP,则OP平分∠AOB的依据是( )
A.SSS B.SAS C.AAS D.HL
3.如图,直角三角形被挡住了一部分,小明根据所学知识很快就另外画出了一个与原来完全一样的三角形,这两个三角形全等的依据是( )
A.SAS B.ASA C.AAS D.HL
4.如图,,,,则的度数为( )
A.20° B.25° C.30° D.35°
5.如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )
A.∠M=∠N B.AM=CN C.AB=CD D.AM∥CN
二、填空题
6.已知 , , 的面积是 ,那么 中 边上的高是 .
7.若△ABC≌△DEF,A与D,B与E分别是对应顶点,∠A=50°,∠B=70°,则∠F= °.
8.如图,的度数为 .
9.如图, △ ,其中 , ,则 .
10.如图,木工师傅做好一门框后钉上木条AB,CD,使门框不变形,这种做法依据的数学原理是 .
11.为了庆祝神舟十五号的成功发射,学校组织了一次小制作展示活动,小明计划制作一个如图所示的简易模型,已知该模型满足,点B和点C是对应顶点,若,,则 .
三、计算题
12.如图,∠C=∠D=90°,DA=CB,∠CBA=28°,求∠DAC.
四、解答题
13.已知:如图,在△ABC中,AB=AC,BD、CE是高.求证:BD=CE.
五、作图题
14.在如图所示的方格纸中,动手画出△DEF和△DEG(F、G不能重合),使得△ABC≌△DEF≌△DEG.(不用直尺画不得分)
六、综合题
15.已知:如图,已知 , , 和 相交于点 ,点 是 的中点,连接 .
(1)求证: ;
(2)求 的度数.
16.如图,点 B 为 AC 上一点,AD//CE,∠ADB = ∠CBE,BD = EB
求证:
(1)△ABD≌△CEB;
(2)AC = AD+ CE.
17.已知:如图,M是AB的中点,∠1=∠2,∠C=∠D,求证:
(1)△AMC≌△BMD;
(2)AC=BD.
答案解析部分
1.【答案】C
【知识点】三角形全等的判定
2.【答案】D
【知识点】三角形全等的判定
3.【答案】B
【知识点】三角形全等的判定-ASA
4.【答案】D
【知识点】三角形内角和定理;三角形全等及其性质
5.【答案】B
【知识点】三角形全等的判定
6.【答案】8
【知识点】三角形的面积;三角形全等及其性质
7.【答案】60
【知识点】三角形内角和定理;三角形全等及其性质
8.【答案】75°
【知识点】角的运算;三角形全等及其性质
9.【答案】
【知识点】三角形全等及其性质
10.【答案】三角形的稳定性
【知识点】三角形的稳定性
11.【答案】5
【知识点】三角形全等及其性质
12.【答案】解:在Rt△ABC和Rt△BAD中, ,
∴Rt△ABC≌Rt△BAD(HL),
∴∠DAB=∠CBA=28°,
∵∠C=90°,
∴∠BAC=90°﹣∠CBA=90°﹣28°=62°,
∴∠DAC=∠BAC﹣∠DAB=62°﹣28°=34°
【知识点】全等三角形的判定与性质
13.【答案】证明:∵BD、CE是高,
∴∠ADB=∠AEC=90°,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(AAS),
∴BD=CE.
【知识点】三角形全等的判定-AAS
14.【答案】解:
【知识点】三角形全等的判定
15.【答案】(1)证明:在 和 中,
,
∴
(2)解:∵ ,
∴ ,
∴ .
∵ 是 的中点,
∴ ,
∴
【知识点】等腰三角形的性质;三角形全等的判定-SSS
16.【答案】(1)证明:∵AD//CE,
∴∠A=∠C,
又∠ADB =
∠CBE,BD = EB
∴△ABD≌△CEB(AAS)
(2)证明:∵△ABD≌△CEB
∴AD=CB,AB=CE
∴AC
= AB+ BC= CE+AD,
即AC = AD+
CE
【知识点】全等三角形的判定与性质
17.【答案】(1)证明:∵点M是AB的中点,
∴AM=BM,
在△AMC和△BMD中,
,
∴△AMC≌△BMD(AAS)
(2)证明:∵△AMC≌△BMD,
∴AC=BD.
【知识点】三角形全等的判定-AAS
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
