三年级上册数学人教版简单枚举课件(共23张PPT)
文档属性
| 名称 | 三年级上册数学人教版简单枚举课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 338.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-10 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
简单枚举
YOUR LOGO
2023秋 第19周
慧解题
01
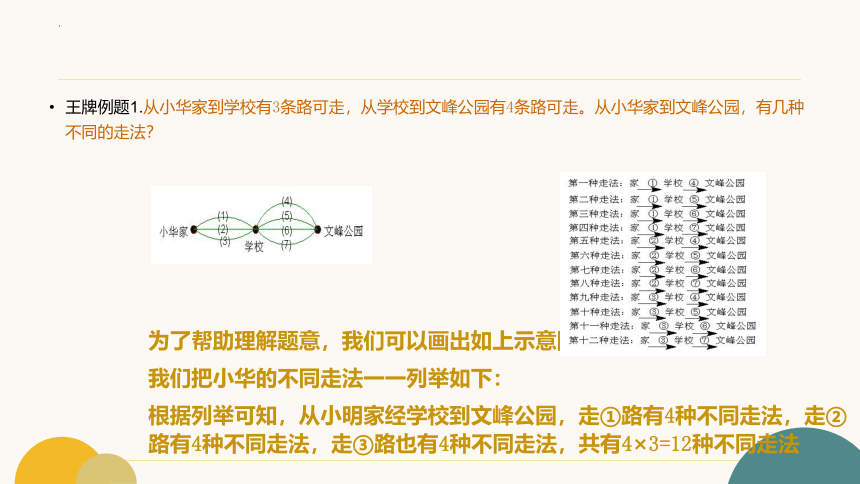
王牌例题1.从小华家到学校有3条路可走,从学校到文峰公园有4条路可走。从小华家到文峰公园,有几种不同的走法?
为了帮助理解题意,我们可以画出如上示意图。
我们把小华的不同走法一一列举如下:
根据列举可知,从小明家经学校到文峰公园,走①路有4种不同走法,走②路有4种不同走法,走③路也有4种不同走法,共有4×3=12种不同走法
练1-1.从甲地到乙地,有3条公路直达,从乙地到丙地有2条铁路直达。从甲地到丙地有多少种不同走法?
3×2=6(种)
答:从甲地到丙地有6种不同走法。
练1-2.书店有3种不同的英语辅导书,4种不同的数学辅导书。小明想买一本英语辅导书和一本数学辅导书。他有多少种不同的买法?
3×4=12(种)
答:共有12种不同买法.
练1-3.
2×3×4=24(种)
答:最多可搭配成24种不同的装束。
明明有2件不同的上衣,3条不同的裤子,4双不同的鞋子。最多可搭配成多少种不同的装束?
王牌例题2.
由于长方形的周长是22米,可知它的长与宽之和为11米。下面列举出符合这个条件的各种长方形:
答:这个长方形的面积有5种可能。
一个长方形的周长是22米,如果它的长和宽都是以米为单位的整数,那么这个长方形的面积有多少种可能?
练2-1.一个长方形的周长是30厘米,如果它的长和宽都是以厘来为单位的整数,那么这个长方形的面积有多少种可能?
那么这个长方形的面积有7种可能。
练2-2.把15个玻璃球分成数量不同的4堆,共有多少种不同的分法?
6种
练2-3.3个自然数的乘积是18,由这样的3个数所组成的数组有多少个?如(1,2,9)就是其中的一个,而且数组中数字相同但顺序不同的算作同一数组,如(1,2,9)和(2,9,1)是同一数组。
4组:(1,1,18) (1,2,9) (1,3,6) (2,3,3)
王牌例题3.4个小朋友在寒假中互相打一次电话,他们一共打了多少次电话?
【思路导航】把4个小朋友分别编号:A,B,C,D。A与其他小朋友打电话,应该打3次,同样B,C,D也应与其他小朋友打了3次电话,4个小朋友共打了3×4=12次电话。题目要求2个小朋友之间只要打一次电话,那么A打电话给B时,A,B两人已打过电话了,所以B没有必要再打电话给A。照这样计算,12次电话中有一半是重复计算的,所以实际打电话的次数是3×4÷2=6次。列式如下:
3×4÷2=6(次)
答:他们一共打了6次电话。
练3-1.6个小队进行排球比赛,每两队比赛一场,一共要进行多少场比赛?
共进行了5×6÷2=15场比赛。
练3-2.小芳参加有19人参与的研讨会,散会后每两人都要握一次手,他们一共握了多少次手?
他们一共握了19×18÷2=171次手。
练3-3.A,B,C,D,E这五个人一起回答一个问题,结果只有两人答对了,答对问题的两人的所有可能的情况共有多少种?
所有可能的回答情况一共有4×5÷2=10种。
王牌例题4.一条铁路共有10个车站。如果每个起点站到终点站只用一种车票(中间至少相隔5个车站),那么这样的车票共有多少种?
【思路导航】我们可用1~10编号,每个号码表示一个车站:
1 2 3 4 5 6 7 8 9 10
可以利用列举的方法:如果起点站是1,那么终点站只能是7.8.9或10:如果起点站是2,那么终点站只能是8,9或10;如果起点站
是3,那么终点站只能是9或10;如果起点站是4,终点站只能是10;如果起点站是5或6时,就找不到与它至少相隔5个车站的终点站了。而起点站是7时,终点站是1;起点站是8时,那终点站是2或
1:起点站是9时,那么终点站是3,2或1;起点站为10时,终点站是
43.2或1。那么起点站到终点站至少相隔5个车站的车票有:
4+3+2+1+0+0+1+2+3+4=20(种)
答:这样的车票有20种。
练4-1.若甲城、乙城、丙城三个城市分别建有一个飞机场,它们之间通航一共需要多少种不同的机票?
(2+1)×2=6(种)
答:它们之间通航一共需要6种不同的机票。
练4-2.小王准备从青岛、北京、海南、桂林4个城市中选2个去旅游,有多少种不同的选择方法?如果小王想去其中的3个城市旅游,又有多少种不同的选择方法?
.要从4个城市中选2个城市,有3+2+1=6种不同的选择方法;要从4个城市中选3个城市,有2+1+1=4种选择方法。
练4-3.一条公路上共有8个站点,如果每个起点站到终点站只用一种车票(中间至少相隔3个车站),那么共有多少种不同的车票?
可以给8个站点按照1~8的顺序从左到右分别编号。如果起点站是1,那么终点站只能是5,6,7,8;如果起点站是2,那么终点站只能是6,7,8;如果起点站是3,那么终点站只能是7,8……以此类推,那么共有4+3+2+1+1+2+3+4=20种不同的车票。
王牌例题例5.小悦买了一些大福娃和一些小福娃,一共不到10个,且两种福娃的个数不一样多。请问两种福娃的个数可能有多少种不同的情况?
【思路导航】当大、小福娃的总数是9个时,大、小福娃的个数可以分别是1,8;2,7;3,6;4,5;5,4;6,3;7,2;8,1,共8种;当大、小福娃的总数是8个时,大、小福娃的个数可以分别是1,7;2,6;3,5;
5,3;6,2;7,1,共6种;当大、小福娃的总数是7个时,大、小福娃的个数可以分别是1,6;2,5;3,4;4,3;5,2;6,1,共6种……当大、小福娃的总数是3个时,大、小福娃的个数可以分别是1,2;2,1,共2种。
所以,两种福娃的个数有8+6+6+4+4+2+2=32种不同的情况。
练5-1.在1~49中,任意取两个和小于50的数,共有多少种不同的取法?
第一个数取1时,另一个数可以是2,3,4,…,48,共47种;
第一个数取2时,另一个数可以是3,4,5,…,47,共45种;
第一个数取3时,另一个数可以是4,5,6,…,46,共43种;
第一个数取24时,另一个数只能取25,共1种。
因此,共47+45+43+…+3+1=576(种)。
练5-2.在算盘上用两颗珠子可以表示多少个不同的四位数?
两颗珠子全在下面:2000,1001,1010,1100
两颗珠子全在上面:5005,5050,5500
两颗珠子上、下各一颗:6000,1005,1050,1500,5001,5010,5100
共有:4+3+7=14(个)
练5-3.十把钥匙开十把锁,但钥匙放乱了,最多要试多少次才可以找到相应的锁?最多要试多少次才能保证打开相应的锁?
(1)第1把钥匙最多要试9次可以找到相应的锁,第2把钥匙最多要试8次才能找到相应的锁,第3把钥匙最多要试7次才能找到相应的锁……第9把钥匙最多要试1次才能找到相应的锁,第10把钥匙不用试了,就是剩下的一把锁。所以最多共要试9+8+7+6+5+4+3+2+1=45次,可以找到相应的锁。
(2)第1把钥匙最多要试10次才能打开相应的锁,第2把钥匙最多要试9次才能打开相应的锁……第10把钥匙要试1次。因此共要试10+9+8+7+6+5+4+3+2+1=55次才能打开相应的锁。
下周 不 见 不 散
YOUR LOGO
祝同学们生活愉快,学习进步!
简单枚举
YOUR LOGO
2023秋 第19周
慧解题
01
王牌例题1.从小华家到学校有3条路可走,从学校到文峰公园有4条路可走。从小华家到文峰公园,有几种不同的走法?
为了帮助理解题意,我们可以画出如上示意图。
我们把小华的不同走法一一列举如下:
根据列举可知,从小明家经学校到文峰公园,走①路有4种不同走法,走②路有4种不同走法,走③路也有4种不同走法,共有4×3=12种不同走法
练1-1.从甲地到乙地,有3条公路直达,从乙地到丙地有2条铁路直达。从甲地到丙地有多少种不同走法?
3×2=6(种)
答:从甲地到丙地有6种不同走法。
练1-2.书店有3种不同的英语辅导书,4种不同的数学辅导书。小明想买一本英语辅导书和一本数学辅导书。他有多少种不同的买法?
3×4=12(种)
答:共有12种不同买法.
练1-3.
2×3×4=24(种)
答:最多可搭配成24种不同的装束。
明明有2件不同的上衣,3条不同的裤子,4双不同的鞋子。最多可搭配成多少种不同的装束?
王牌例题2.
由于长方形的周长是22米,可知它的长与宽之和为11米。下面列举出符合这个条件的各种长方形:
答:这个长方形的面积有5种可能。
一个长方形的周长是22米,如果它的长和宽都是以米为单位的整数,那么这个长方形的面积有多少种可能?
练2-1.一个长方形的周长是30厘米,如果它的长和宽都是以厘来为单位的整数,那么这个长方形的面积有多少种可能?
那么这个长方形的面积有7种可能。
练2-2.把15个玻璃球分成数量不同的4堆,共有多少种不同的分法?
6种
练2-3.3个自然数的乘积是18,由这样的3个数所组成的数组有多少个?如(1,2,9)就是其中的一个,而且数组中数字相同但顺序不同的算作同一数组,如(1,2,9)和(2,9,1)是同一数组。
4组:(1,1,18) (1,2,9) (1,3,6) (2,3,3)
王牌例题3.4个小朋友在寒假中互相打一次电话,他们一共打了多少次电话?
【思路导航】把4个小朋友分别编号:A,B,C,D。A与其他小朋友打电话,应该打3次,同样B,C,D也应与其他小朋友打了3次电话,4个小朋友共打了3×4=12次电话。题目要求2个小朋友之间只要打一次电话,那么A打电话给B时,A,B两人已打过电话了,所以B没有必要再打电话给A。照这样计算,12次电话中有一半是重复计算的,所以实际打电话的次数是3×4÷2=6次。列式如下:
3×4÷2=6(次)
答:他们一共打了6次电话。
练3-1.6个小队进行排球比赛,每两队比赛一场,一共要进行多少场比赛?
共进行了5×6÷2=15场比赛。
练3-2.小芳参加有19人参与的研讨会,散会后每两人都要握一次手,他们一共握了多少次手?
他们一共握了19×18÷2=171次手。
练3-3.A,B,C,D,E这五个人一起回答一个问题,结果只有两人答对了,答对问题的两人的所有可能的情况共有多少种?
所有可能的回答情况一共有4×5÷2=10种。
王牌例题4.一条铁路共有10个车站。如果每个起点站到终点站只用一种车票(中间至少相隔5个车站),那么这样的车票共有多少种?
【思路导航】我们可用1~10编号,每个号码表示一个车站:
1 2 3 4 5 6 7 8 9 10
可以利用列举的方法:如果起点站是1,那么终点站只能是7.8.9或10:如果起点站是2,那么终点站只能是8,9或10;如果起点站
是3,那么终点站只能是9或10;如果起点站是4,终点站只能是10;如果起点站是5或6时,就找不到与它至少相隔5个车站的终点站了。而起点站是7时,终点站是1;起点站是8时,那终点站是2或
1:起点站是9时,那么终点站是3,2或1;起点站为10时,终点站是
43.2或1。那么起点站到终点站至少相隔5个车站的车票有:
4+3+2+1+0+0+1+2+3+4=20(种)
答:这样的车票有20种。
练4-1.若甲城、乙城、丙城三个城市分别建有一个飞机场,它们之间通航一共需要多少种不同的机票?
(2+1)×2=6(种)
答:它们之间通航一共需要6种不同的机票。
练4-2.小王准备从青岛、北京、海南、桂林4个城市中选2个去旅游,有多少种不同的选择方法?如果小王想去其中的3个城市旅游,又有多少种不同的选择方法?
.要从4个城市中选2个城市,有3+2+1=6种不同的选择方法;要从4个城市中选3个城市,有2+1+1=4种选择方法。
练4-3.一条公路上共有8个站点,如果每个起点站到终点站只用一种车票(中间至少相隔3个车站),那么共有多少种不同的车票?
可以给8个站点按照1~8的顺序从左到右分别编号。如果起点站是1,那么终点站只能是5,6,7,8;如果起点站是2,那么终点站只能是6,7,8;如果起点站是3,那么终点站只能是7,8……以此类推,那么共有4+3+2+1+1+2+3+4=20种不同的车票。
王牌例题例5.小悦买了一些大福娃和一些小福娃,一共不到10个,且两种福娃的个数不一样多。请问两种福娃的个数可能有多少种不同的情况?
【思路导航】当大、小福娃的总数是9个时,大、小福娃的个数可以分别是1,8;2,7;3,6;4,5;5,4;6,3;7,2;8,1,共8种;当大、小福娃的总数是8个时,大、小福娃的个数可以分别是1,7;2,6;3,5;
5,3;6,2;7,1,共6种;当大、小福娃的总数是7个时,大、小福娃的个数可以分别是1,6;2,5;3,4;4,3;5,2;6,1,共6种……当大、小福娃的总数是3个时,大、小福娃的个数可以分别是1,2;2,1,共2种。
所以,两种福娃的个数有8+6+6+4+4+2+2=32种不同的情况。
练5-1.在1~49中,任意取两个和小于50的数,共有多少种不同的取法?
第一个数取1时,另一个数可以是2,3,4,…,48,共47种;
第一个数取2时,另一个数可以是3,4,5,…,47,共45种;
第一个数取3时,另一个数可以是4,5,6,…,46,共43种;
第一个数取24时,另一个数只能取25,共1种。
因此,共47+45+43+…+3+1=576(种)。
练5-2.在算盘上用两颗珠子可以表示多少个不同的四位数?
两颗珠子全在下面:2000,1001,1010,1100
两颗珠子全在上面:5005,5050,5500
两颗珠子上、下各一颗:6000,1005,1050,1500,5001,5010,5100
共有:4+3+7=14(个)
练5-3.十把钥匙开十把锁,但钥匙放乱了,最多要试多少次才可以找到相应的锁?最多要试多少次才能保证打开相应的锁?
(1)第1把钥匙最多要试9次可以找到相应的锁,第2把钥匙最多要试8次才能找到相应的锁,第3把钥匙最多要试7次才能找到相应的锁……第9把钥匙最多要试1次才能找到相应的锁,第10把钥匙不用试了,就是剩下的一把锁。所以最多共要试9+8+7+6+5+4+3+2+1=45次,可以找到相应的锁。
(2)第1把钥匙最多要试10次才能打开相应的锁,第2把钥匙最多要试9次才能打开相应的锁……第10把钥匙要试1次。因此共要试10+9+8+7+6+5+4+3+2+1=55次才能打开相应的锁。
下周 不 见 不 散
YOUR LOGO
祝同学们生活愉快,学习进步!
同课章节目录
