1.3位置变化快慢的描述—速度(课件)-【扬帆起航系列】高中物理同步备课(人教版2019必修第一册)
文档属性
| 名称 | 1.3位置变化快慢的描述—速度(课件)-【扬帆起航系列】高中物理同步备课(人教版2019必修第一册) |

|
|
| 格式 | pptx | ||
| 文件大小 | 35.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-07-30 15:54:08 | ||
图片预览









文档简介
(共46张PPT)
1.3 位置变化快慢的描述—速度
【扬帆起航系列】2024-2025学年高中物理同步备课必修第一册
授课人:扬帆起航
新人教版(2019)
第一章 运动的描述
01
速度
02
平均速度和瞬时速度
目录/contents
03
典例分析
新课导入
生活和科学研究中经常需要知道物体运动的快慢和方向,你还记得初中是怎样描述物体运动快慢的吗?运动员在比赛中的不同时段,运动的快慢一样吗?
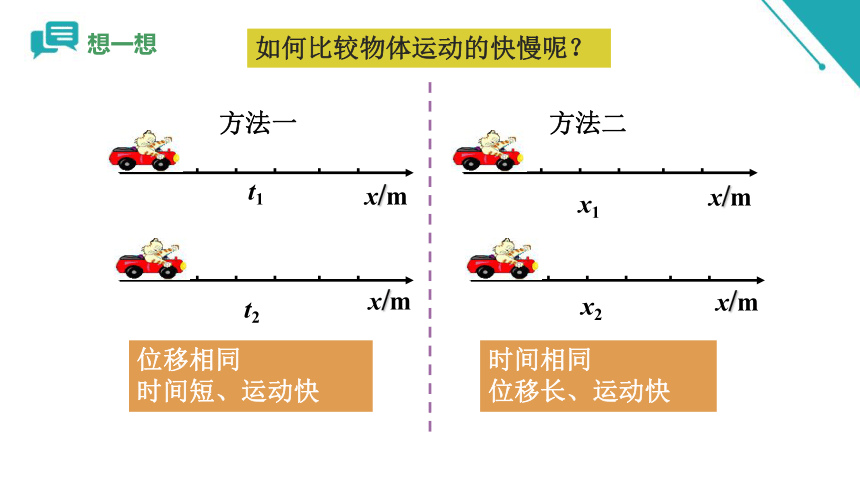
如何比较物体运动的快慢呢?
方法二
方法一
x/m
x/m
位移相同
时间短、运动快
x/m
x/m
时间相同
位移长、运动快
t1
t2
x1
x2
想一想
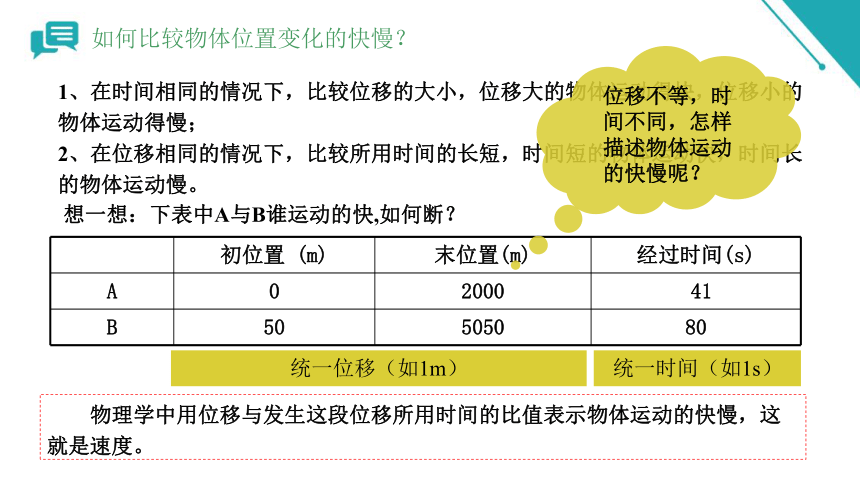
如何比较物体位置变化的快慢?
1、在时间相同的情况下,比较位移的大小,位移大的物体运动得快,位移小的物体运动得慢;
2、在位移相同的情况下,比较所用时间的长短,时间短的物体运动快,时间长的物体运动慢。
想一想:下表中A与B谁运动的快,如何断?
初位置 (m) 末位置(m) 经过时间(s)
A 0 2000 41
B 50 5050 80
统一位移(如1m)
统一时间(如1s)
位移不等,时间不同,怎样描述物体运动的快慢呢?
物理学中用位移与发生这段位移所用时间的比值表示物体运动的快慢,这就是速度。
速度(velocity)
01
1、速度定义:位移与发生这个位移所用时间的比值
v=
2、定义式:
3、物理意义:表示物体运动快慢(位置变化快慢)和方向的物理量
4、 国际单位: 米每秒(m/s)、
常用单位: 千米每时(km/h)、厘米每秒(cm/s)等
1m/s=3.6km/h
大小
方向
单位时间内的位移大小
与物体运动的方向相同
5、矢量性:
△x 越大,v越大吗?
比值定义法
速度
两辆汽车从某地出发,速度都是20m/s,他们的运动情况完全相同吗?
—— 可能是背道而驰 !!
体会:速度仅指出大小是不够的,
还必须具有______
方向
注意:求矢量时既要求出大小,同时还要指出方向!
想一想
【例题】下列关于速度的说法不正确的是 ( )
A. 速度描述物体运动的快慢,只有大小
B. 物体运动时间越短,速度越大
C. 物体运动位移越大,速度越大
D. 物体位置变化越快,速度越大
ABC
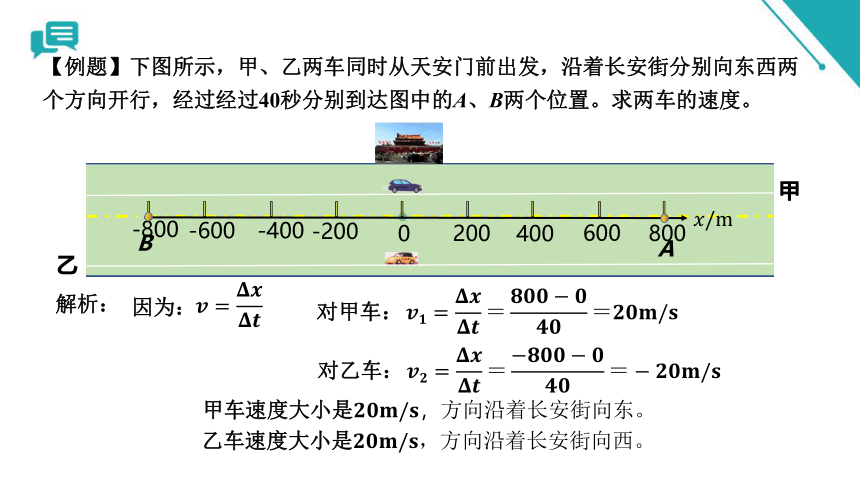
【例题】下图所示,甲、乙两车同时从天安门前出发,沿着长安街分别向东西两个方向开行,经过经过40秒分别到达图中的A、B两个位置。求两车的速度。
0
200
400
600
800
-200
-400
-600
-800
A
B
解析:
乙
甲
因为:
对甲车:
对乙车:
甲车速度大小是
乙车速度大小是
生活中的速度
中国高铁时速可达250-350km/h
火箭发射时速度约为4500m/s
生活中的速度
交通工具的速度是不是越快越好?
龟兔赛跑,谁跑得更快一点呢?
想一想
解析:
【例题】龟兔赛跑的位移时间如图所示。
⑴求龟的速度;⑵求兔的速度;⑶分析说明兔的运动过程。
⑴龟的速度:
⑵兔的速度:
⑶兔的运动过程可分为三个阶段:
①兔的速度是20米/分,跑了10分钟;
②兔睡觉40分钟;
③兔的速度是30米/分,跑了10分钟。
x-t图像是一条直线,直线的斜率等于物体运动的速度。
龟兔赛跑龟胜了,只反应了在赛跑过程中兔跑步的平均效果,而不能反应兔跑步快慢的真实情况。
平均速度和瞬时速度
02
(1)定义:位移与发生这个位移所用时间的比值,叫做物体在这段时间(或这段位移)内的平均速度。
(2)定义:
(3)物理意义:粗略地描述物体在某段时间内运动的平均快慢和方向。
(4)平均速度的方向:与所对应时间内位移方向相同。
(5)注意:计算物体的平均速度时必须指明物体是在哪段时间内或哪段位移上的平均速度。
(6)平均速度是从整体上来研究物体的运动情况的,平均速度不考虑运动过程的细节问题,只考虑初末位置及整个过程的运动时间问题.描述的是物体(质点)在某段时间内或某段位移内运动的平均快慢(位置改变的大致状况)。
(7) ★平均速度的大小不能叫做平均速率。
时间越短,描述越准确
平均速率
1、平均速度
解析:
【例题】有三个物体甲、乙、丙,同时从O点出发,在相同时间(10秒)内都走过了70米的路程,分别到达C、B、A三点,求三个物体的平均速度和平均速率。
平均速度:
甲的平均速度:
乙的平均速度:
丙的平均速度:
取向东方向为正方向
方向与规定正方向相反——向西
方向东偏北530
平均速率:
甲的平均速率:
乙的平均速率:
丙的平均速率:
路程除以时间得到的值是相等的,但三个物体最终到达位置是不同的,因此用路程除以时间不能体现这种差异,而用位移与时间的比可以反应位置变化上的不同。
平均速度描述物体在一段时间内运动的平均快慢程度及方向。那么,怎样描述物体在某一时刻运动的快慢和方向呢
如:怎样求图中5秒末的速度?
思考与讨论
(1)在数学一次函数y=kx+b所对应的图像中,用斜率表示图线倾斜程度大小,公式中的K值即为直线的斜率。
(2)斜率的定义:
(3)斜率的正负:
①若Δy与Δx同号时,即图线向上倾斜(过1、3象限),斜率为正;
②若Δy与Δx异号时,即图线向下倾斜(过2、4象限),斜率为负。
x
A
B
y2
y1
x2
x1
Δx
Δy
y
C
D
x
y2
y1
x2
x1
Δx
Δy
y
数学知识补充
如:怎样求图中5秒末的速度?
先求5~9秒内的平均速度
等于直线AB的斜率
再求5~8秒内的平均速度
—图像中过某一点的切线的斜率等于该点所对应时刻的速度
比较和
距5秒末的时间间隔趋近于0时的平均速度等于5秒末的速度。
等于直线AC的斜率
这种处理方式用到了数学中极限的知识。
当△t 非常非常小时(接近于0), 就可以看做某时刻(或某位置)的瞬时速度。(极限思想)
△x
△x
x/m
A
求出的是物体在△t内的平均速度。
v =
——
Δ t
Δ x
_
极限
Δ t→0
平均速度
瞬时速度
用由时刻t到t +Δt 一小段时间内的平均速度来代替时刻t物体的速度,如果Δt取得小一些,物体在Δt这样一个较小的时间内,运动快慢的差异就不会太大。Δt越小,运动快慢的差异就越小。当Δt非常非常小时,运动快慢的差异可以忽略不计,此时,我们就把叫作物体在时刻t的瞬时速度。
物体在某一时刻或经过某一位置的速度。
2、瞬时速度
(1)定义:
(3)物理意义:精确描述物体运动的快慢和方向。
(2)定义式:
→0
x/m
1
0
2
3
4
5
6
x = 3 m
t/s
1
0
2
3
4
5
6
t = 3 s
瞬时速度
某一位置
某一时刻
(4)方向:这一时刻物体的运动方向。即物体在运动轨迹上过该点的切线方向.
(5)匀速直线运动
匀速直线运动,平均速度与瞬时速度相等。
瞬时速度保持不变的运动
(6)速率
瞬时速度的大小通常叫作速率。速率是标量,只有大小,没有方向.
汽车速度计不能显示车辆运动的方向,它的示数实际是汽车的速率 。日常生活中说到的“速度”,有时是指速率。 要根据上下文判断。
1.平均速度和瞬时速度的区别与联系
物理量 比较项目 平均速度 瞬时速度
区 别 对应关系 与一段时间或一段位移对应 与某一时刻或某一位置对应
物理意义 粗略地描述做变速直线运动的物体在某段时间内或某段位移上的平均快慢程度 精确地描述做变速直线运动的物体在某时刻或某位置时的快慢程度
方向 与所对应时间内位移方向相同 物体在该时刻的运动方向
联系 (1)在公式v=中,Δt→0时,平均速度即为瞬时速度 (2)匀速直线运动中,任意一段时间内的平均速度等于任意时刻的瞬时速度 2.平均速度和平均速率的区别与联系
平均速度 瞬时速度 平均速率 速率
定义
方向
意义
对应
与位移 x方向相同
运动质点的位移与时间的比值
运动质点在某一时刻(或位置)的速度
瞬时速度的大小
运动质点的路程与时间的比值
此时刻的运动方向,即物体在运动轨迹上过该点的切线方向
无方向,标量
无方向,标量
精确描述物体运动的快慢
某段时间(或位移)
精确描述物体运动的快慢
粗略描述物体运动的快慢
粗略描述物体运动的快慢
某一时刻(或位置)
某段时间(或路程)
某一时刻(或位置)
典例分析
03
×
×
×
√
×
√
|基础小题·做一做|
2、甲、乙两地直线距离为20 km.
(1)小明开车从甲地到乙地,用时20分钟,他的平均速度多大?
答案 此时刻的速率为70 km/h.
(2)途中某时刻,小明发现速度计示数为70 km/h,此示数表示什么?
答案 因为全程的位移为零,所以平均速度为0 不能
(3)若小明由乙地返回甲地又用了20分钟,则从甲地出发又返回甲地的整个过程的平均速度是多少?它能反映汽车运动的快慢吗?
【例题】甲、乙两质点在同一直线上匀速运动,设向右为正,甲质点的速度为2m/s,乙质点的速度为-4m/s,则可知( )
A.乙质点的速率大于甲质点的速率
B.因为2>-4,所以甲质点的速度大于乙质点的速度
C.这里的正、负号的物理意义是表示运动的方向
D.若甲、乙两质点同时由同一点出发,则10 s后甲、乙两质点相距60 m
ACD
解析:因为速度是矢量,所以其正、负号表示物体的运动方向,选项C正确。速率是标量,等于速度的大小,甲、乙的速率分别为2 m/s、4 m/s,故选项A正确。速度是矢量,其正、负不表示大小,只有速度的数值才能比较大小,选项B错误;甲、乙两质点在同一直线上沿相反方向运动,10 s后的距离等于两者位移大小之和,计算可得选项D正确。
答案 :ACD
【例题】关于速度的定义式v = ,以下叙述正确的是( )
A.物体做匀速直线运动时,速度v与运动的位移Δx成正比,与运动时间Δt成反比
B.速度v的大小与运动的位移Δx和时间Δt都无关
C.此速度定义式适用于任何运动
D.速度是表示物体运动快慢及方向的物理量
解析: v = 是计算速度的公式,适用于任何运动,C对;此式只说明速度可用位移Δx除以时间Δt来计算,并不是说v与Δx成正比,与Δt成反比,A错,B对;速度的大小表示物体运动的快慢,方向表示物体的运动方向,D对。
BCD
【例题】关于瞬时速度和平均速度的说法,正确的是( )
A.平均速度一定等于初速度与末速度的平均值
B.匀速直线运动的平均速度等于瞬时速度
C.平均速度为0的物体,一定始终处于静止状态
D.任意时刻瞬时速度都相等的两个物体,它们的平均速度不一定相等
解析:只有匀加速直线运动,平均速度才等于初速度与末速度的平均值,故A错误;匀速直线运动的速度保持不变,各段时间内的平均速度等于瞬时速度,故B正确;平均速度只能粗略反映物体的运动,平均速度为零,只能说明物体在一段时间内回到了出发点;不能说明物体一定静止,故C错误;任意时刻瞬时速度都相等的两个物体,它们在相等时间内通过的位移相等,所以它们的平均速度一定相等,故D错误。
B
【例题】小蒙骑自行车由静止沿直线运动,他在第1s内、第2s内、第3s内、第4s内通过的位移分别为1m、2m、3m、4m,则( )
A.他4s末的瞬时速度为4m/s
B.他第2s内的平均速度为1.5m/s
C.他4s内的平均速度为2.5m/s
D.他1s末的速度为1m/s
解析:自行车速度逐渐增大的,无法确定它的瞬时速度,只能求出平均速度,第2 s内平均速度为 m/s=2 m/s;4 s内的平均速度 m/s
=2.5 m/s。
答案:C
【例题】(多选)(2021·广西·钟山中学高一阶段练习)甲乙两同学同时从学校出发前往书城,甲步行,乙骑自行车,路线如图,两人同时到达书城,则( )
A.甲乙的平均速度相等 B.甲的平均速度较大
C.甲的平均速率较大 D.甲的平均速率较小
AD
【例题】某质点由A出发做直线运动,前5 s向东运动了30 m经过B点,又运动了5 s前进了60 m到达C点,在C点停了4 s后又向西运动,经历了6 s运动120 m到达A点西侧的D点,如图所示,求:
(1)全过程的平均速度。
(2)全过程的平均速率。
答案:(1)1.5 m/s 方向向西 (2)10.5 m/s
例6.一物体沿正东方向以4m/s的速度匀速运动4s,又以3m/s的速度向北匀速运动4s,求这8s内物体的平均速度和平均速率(tan 37°=0.75)。
答案:平均速度大小2.5 m/s,方向为东偏北37° 平均速率为3.5 m/s
B
C
D
A
【例题】小虫沿小桌边缘由A点开始顺时针爬行一周所用时间为t,桌面为正方形,边长为l,求:小虫由A再次爬回到A这个过程的平均速度及平均速率.
【例题】物体沿直线运动。
⑴前一半时间的平均速度是20m/s,后一半时间的平均速度是30m/s,物体全程的平均速度是多少?
⑵前半段位移的平均速度是20m/s,后半段位移的平均速度是30m/s,则物体全程的平均速度多少?
⑴ =
=
⑵
解:
1.3 位置变化快慢的描述—速度
【扬帆起航系列】2024-2025学年高中物理同步备课必修第一册
授课人:扬帆起航
新人教版(2019)
第一章 运动的描述
01
速度
02
平均速度和瞬时速度
目录/contents
03
典例分析
新课导入
生活和科学研究中经常需要知道物体运动的快慢和方向,你还记得初中是怎样描述物体运动快慢的吗?运动员在比赛中的不同时段,运动的快慢一样吗?
如何比较物体运动的快慢呢?
方法二
方法一
x/m
x/m
位移相同
时间短、运动快
x/m
x/m
时间相同
位移长、运动快
t1
t2
x1
x2
想一想
如何比较物体位置变化的快慢?
1、在时间相同的情况下,比较位移的大小,位移大的物体运动得快,位移小的物体运动得慢;
2、在位移相同的情况下,比较所用时间的长短,时间短的物体运动快,时间长的物体运动慢。
想一想:下表中A与B谁运动的快,如何断?
初位置 (m) 末位置(m) 经过时间(s)
A 0 2000 41
B 50 5050 80
统一位移(如1m)
统一时间(如1s)
位移不等,时间不同,怎样描述物体运动的快慢呢?
物理学中用位移与发生这段位移所用时间的比值表示物体运动的快慢,这就是速度。
速度(velocity)
01
1、速度定义:位移与发生这个位移所用时间的比值
v=
2、定义式:
3、物理意义:表示物体运动快慢(位置变化快慢)和方向的物理量
4、 国际单位: 米每秒(m/s)、
常用单位: 千米每时(km/h)、厘米每秒(cm/s)等
1m/s=3.6km/h
大小
方向
单位时间内的位移大小
与物体运动的方向相同
5、矢量性:
△x 越大,v越大吗?
比值定义法
速度
两辆汽车从某地出发,速度都是20m/s,他们的运动情况完全相同吗?
—— 可能是背道而驰 !!
体会:速度仅指出大小是不够的,
还必须具有______
方向
注意:求矢量时既要求出大小,同时还要指出方向!
想一想
【例题】下列关于速度的说法不正确的是 ( )
A. 速度描述物体运动的快慢,只有大小
B. 物体运动时间越短,速度越大
C. 物体运动位移越大,速度越大
D. 物体位置变化越快,速度越大
ABC
【例题】下图所示,甲、乙两车同时从天安门前出发,沿着长安街分别向东西两个方向开行,经过经过40秒分别到达图中的A、B两个位置。求两车的速度。
0
200
400
600
800
-200
-400
-600
-800
A
B
解析:
乙
甲
因为:
对甲车:
对乙车:
甲车速度大小是
乙车速度大小是
生活中的速度
中国高铁时速可达250-350km/h
火箭发射时速度约为4500m/s
生活中的速度
交通工具的速度是不是越快越好?
龟兔赛跑,谁跑得更快一点呢?
想一想
解析:
【例题】龟兔赛跑的位移时间如图所示。
⑴求龟的速度;⑵求兔的速度;⑶分析说明兔的运动过程。
⑴龟的速度:
⑵兔的速度:
⑶兔的运动过程可分为三个阶段:
①兔的速度是20米/分,跑了10分钟;
②兔睡觉40分钟;
③兔的速度是30米/分,跑了10分钟。
x-t图像是一条直线,直线的斜率等于物体运动的速度。
龟兔赛跑龟胜了,只反应了在赛跑过程中兔跑步的平均效果,而不能反应兔跑步快慢的真实情况。
平均速度和瞬时速度
02
(1)定义:位移与发生这个位移所用时间的比值,叫做物体在这段时间(或这段位移)内的平均速度。
(2)定义:
(3)物理意义:粗略地描述物体在某段时间内运动的平均快慢和方向。
(4)平均速度的方向:与所对应时间内位移方向相同。
(5)注意:计算物体的平均速度时必须指明物体是在哪段时间内或哪段位移上的平均速度。
(6)平均速度是从整体上来研究物体的运动情况的,平均速度不考虑运动过程的细节问题,只考虑初末位置及整个过程的运动时间问题.描述的是物体(质点)在某段时间内或某段位移内运动的平均快慢(位置改变的大致状况)。
(7) ★平均速度的大小不能叫做平均速率。
时间越短,描述越准确
平均速率
1、平均速度
解析:
【例题】有三个物体甲、乙、丙,同时从O点出发,在相同时间(10秒)内都走过了70米的路程,分别到达C、B、A三点,求三个物体的平均速度和平均速率。
平均速度:
甲的平均速度:
乙的平均速度:
丙的平均速度:
取向东方向为正方向
方向与规定正方向相反——向西
方向东偏北530
平均速率:
甲的平均速率:
乙的平均速率:
丙的平均速率:
路程除以时间得到的值是相等的,但三个物体最终到达位置是不同的,因此用路程除以时间不能体现这种差异,而用位移与时间的比可以反应位置变化上的不同。
平均速度描述物体在一段时间内运动的平均快慢程度及方向。那么,怎样描述物体在某一时刻运动的快慢和方向呢
如:怎样求图中5秒末的速度?
思考与讨论
(1)在数学一次函数y=kx+b所对应的图像中,用斜率表示图线倾斜程度大小,公式中的K值即为直线的斜率。
(2)斜率的定义:
(3)斜率的正负:
①若Δy与Δx同号时,即图线向上倾斜(过1、3象限),斜率为正;
②若Δy与Δx异号时,即图线向下倾斜(过2、4象限),斜率为负。
x
A
B
y2
y1
x2
x1
Δx
Δy
y
C
D
x
y2
y1
x2
x1
Δx
Δy
y
数学知识补充
如:怎样求图中5秒末的速度?
先求5~9秒内的平均速度
等于直线AB的斜率
再求5~8秒内的平均速度
—图像中过某一点的切线的斜率等于该点所对应时刻的速度
比较和
距5秒末的时间间隔趋近于0时的平均速度等于5秒末的速度。
等于直线AC的斜率
这种处理方式用到了数学中极限的知识。
当△t 非常非常小时(接近于0), 就可以看做某时刻(或某位置)的瞬时速度。(极限思想)
△x
△x
x/m
A
求出的是物体在△t内的平均速度。
v =
——
Δ t
Δ x
_
极限
Δ t→0
平均速度
瞬时速度
用由时刻t到t +Δt 一小段时间内的平均速度来代替时刻t物体的速度,如果Δt取得小一些,物体在Δt这样一个较小的时间内,运动快慢的差异就不会太大。Δt越小,运动快慢的差异就越小。当Δt非常非常小时,运动快慢的差异可以忽略不计,此时,我们就把叫作物体在时刻t的瞬时速度。
物体在某一时刻或经过某一位置的速度。
2、瞬时速度
(1)定义:
(3)物理意义:精确描述物体运动的快慢和方向。
(2)定义式:
→0
x/m
1
0
2
3
4
5
6
x = 3 m
t/s
1
0
2
3
4
5
6
t = 3 s
瞬时速度
某一位置
某一时刻
(4)方向:这一时刻物体的运动方向。即物体在运动轨迹上过该点的切线方向.
(5)匀速直线运动
匀速直线运动,平均速度与瞬时速度相等。
瞬时速度保持不变的运动
(6)速率
瞬时速度的大小通常叫作速率。速率是标量,只有大小,没有方向.
汽车速度计不能显示车辆运动的方向,它的示数实际是汽车的速率 。日常生活中说到的“速度”,有时是指速率。 要根据上下文判断。
1.平均速度和瞬时速度的区别与联系
物理量 比较项目 平均速度 瞬时速度
区 别 对应关系 与一段时间或一段位移对应 与某一时刻或某一位置对应
物理意义 粗略地描述做变速直线运动的物体在某段时间内或某段位移上的平均快慢程度 精确地描述做变速直线运动的物体在某时刻或某位置时的快慢程度
方向 与所对应时间内位移方向相同 物体在该时刻的运动方向
联系 (1)在公式v=中,Δt→0时,平均速度即为瞬时速度 (2)匀速直线运动中,任意一段时间内的平均速度等于任意时刻的瞬时速度 2.平均速度和平均速率的区别与联系
平均速度 瞬时速度 平均速率 速率
定义
方向
意义
对应
与位移 x方向相同
运动质点的位移与时间的比值
运动质点在某一时刻(或位置)的速度
瞬时速度的大小
运动质点的路程与时间的比值
此时刻的运动方向,即物体在运动轨迹上过该点的切线方向
无方向,标量
无方向,标量
精确描述物体运动的快慢
某段时间(或位移)
精确描述物体运动的快慢
粗略描述物体运动的快慢
粗略描述物体运动的快慢
某一时刻(或位置)
某段时间(或路程)
某一时刻(或位置)
典例分析
03
×
×
×
√
×
√
|基础小题·做一做|
2、甲、乙两地直线距离为20 km.
(1)小明开车从甲地到乙地,用时20分钟,他的平均速度多大?
答案 此时刻的速率为70 km/h.
(2)途中某时刻,小明发现速度计示数为70 km/h,此示数表示什么?
答案 因为全程的位移为零,所以平均速度为0 不能
(3)若小明由乙地返回甲地又用了20分钟,则从甲地出发又返回甲地的整个过程的平均速度是多少?它能反映汽车运动的快慢吗?
【例题】甲、乙两质点在同一直线上匀速运动,设向右为正,甲质点的速度为2m/s,乙质点的速度为-4m/s,则可知( )
A.乙质点的速率大于甲质点的速率
B.因为2>-4,所以甲质点的速度大于乙质点的速度
C.这里的正、负号的物理意义是表示运动的方向
D.若甲、乙两质点同时由同一点出发,则10 s后甲、乙两质点相距60 m
ACD
解析:因为速度是矢量,所以其正、负号表示物体的运动方向,选项C正确。速率是标量,等于速度的大小,甲、乙的速率分别为2 m/s、4 m/s,故选项A正确。速度是矢量,其正、负不表示大小,只有速度的数值才能比较大小,选项B错误;甲、乙两质点在同一直线上沿相反方向运动,10 s后的距离等于两者位移大小之和,计算可得选项D正确。
答案 :ACD
【例题】关于速度的定义式v = ,以下叙述正确的是( )
A.物体做匀速直线运动时,速度v与运动的位移Δx成正比,与运动时间Δt成反比
B.速度v的大小与运动的位移Δx和时间Δt都无关
C.此速度定义式适用于任何运动
D.速度是表示物体运动快慢及方向的物理量
解析: v = 是计算速度的公式,适用于任何运动,C对;此式只说明速度可用位移Δx除以时间Δt来计算,并不是说v与Δx成正比,与Δt成反比,A错,B对;速度的大小表示物体运动的快慢,方向表示物体的运动方向,D对。
BCD
【例题】关于瞬时速度和平均速度的说法,正确的是( )
A.平均速度一定等于初速度与末速度的平均值
B.匀速直线运动的平均速度等于瞬时速度
C.平均速度为0的物体,一定始终处于静止状态
D.任意时刻瞬时速度都相等的两个物体,它们的平均速度不一定相等
解析:只有匀加速直线运动,平均速度才等于初速度与末速度的平均值,故A错误;匀速直线运动的速度保持不变,各段时间内的平均速度等于瞬时速度,故B正确;平均速度只能粗略反映物体的运动,平均速度为零,只能说明物体在一段时间内回到了出发点;不能说明物体一定静止,故C错误;任意时刻瞬时速度都相等的两个物体,它们在相等时间内通过的位移相等,所以它们的平均速度一定相等,故D错误。
B
【例题】小蒙骑自行车由静止沿直线运动,他在第1s内、第2s内、第3s内、第4s内通过的位移分别为1m、2m、3m、4m,则( )
A.他4s末的瞬时速度为4m/s
B.他第2s内的平均速度为1.5m/s
C.他4s内的平均速度为2.5m/s
D.他1s末的速度为1m/s
解析:自行车速度逐渐增大的,无法确定它的瞬时速度,只能求出平均速度,第2 s内平均速度为 m/s=2 m/s;4 s内的平均速度 m/s
=2.5 m/s。
答案:C
【例题】(多选)(2021·广西·钟山中学高一阶段练习)甲乙两同学同时从学校出发前往书城,甲步行,乙骑自行车,路线如图,两人同时到达书城,则( )
A.甲乙的平均速度相等 B.甲的平均速度较大
C.甲的平均速率较大 D.甲的平均速率较小
AD
【例题】某质点由A出发做直线运动,前5 s向东运动了30 m经过B点,又运动了5 s前进了60 m到达C点,在C点停了4 s后又向西运动,经历了6 s运动120 m到达A点西侧的D点,如图所示,求:
(1)全过程的平均速度。
(2)全过程的平均速率。
答案:(1)1.5 m/s 方向向西 (2)10.5 m/s
例6.一物体沿正东方向以4m/s的速度匀速运动4s,又以3m/s的速度向北匀速运动4s,求这8s内物体的平均速度和平均速率(tan 37°=0.75)。
答案:平均速度大小2.5 m/s,方向为东偏北37° 平均速率为3.5 m/s
B
C
D
A
【例题】小虫沿小桌边缘由A点开始顺时针爬行一周所用时间为t,桌面为正方形,边长为l,求:小虫由A再次爬回到A这个过程的平均速度及平均速率.
【例题】物体沿直线运动。
⑴前一半时间的平均速度是20m/s,后一半时间的平均速度是30m/s,物体全程的平均速度是多少?
⑵前半段位移的平均速度是20m/s,后半段位移的平均速度是30m/s,则物体全程的平均速度多少?
⑴ =
=
⑵
解:
