五年级下册数学人教版第7讲 长方体与正方体(四)(课件)(共27张PPT)
文档属性
| 名称 | 五年级下册数学人教版第7讲 长方体与正方体(四)(课件)(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 448.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-10 17:03:17 | ||
图片预览





文档简介
(共27张PPT)
长方体与正方体(四)
第 7 讲
专题解析
专题分享
课后巩固
专题附加
专题解析
1.
1.长方体的体积=长×宽×高 V=abh
2.正方体的体积=棱长×棱长×棱长 V=a×a×a = a3
3.*形状不规则的物体可以用排水法求体积,形状规则的物体可以用公式直接求体积。
排水法的公式:
V物体 =V现在-V原来
也可以 V物体 =S×(h现在- h原来)
V物体 =S×h升高
专题解析
专题分享
2.
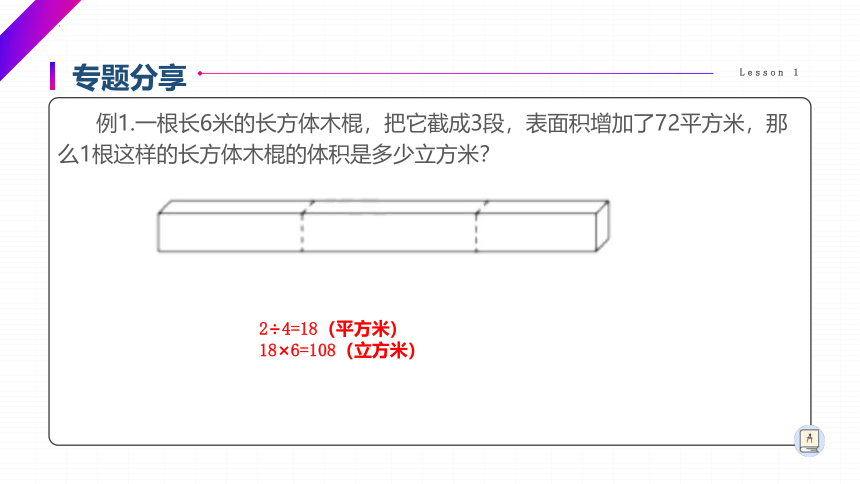
例1.一根长6米的长方体木棍,把它截成3段,表面积增加了72平方米,那么1根这样的长方体木棍的体积是多少立方米?
专题分享
2÷4=18(平方米)
18×6=108(立方米)
练习1-1.如图,三根长度均为20米的长方体木棍粘合在一起,表面积减少了64平方米,那么粘合后的长方体木棍的体积是多少立方米
专题分享
64÷4=16(平方米)
16×20×3=960(立方米)
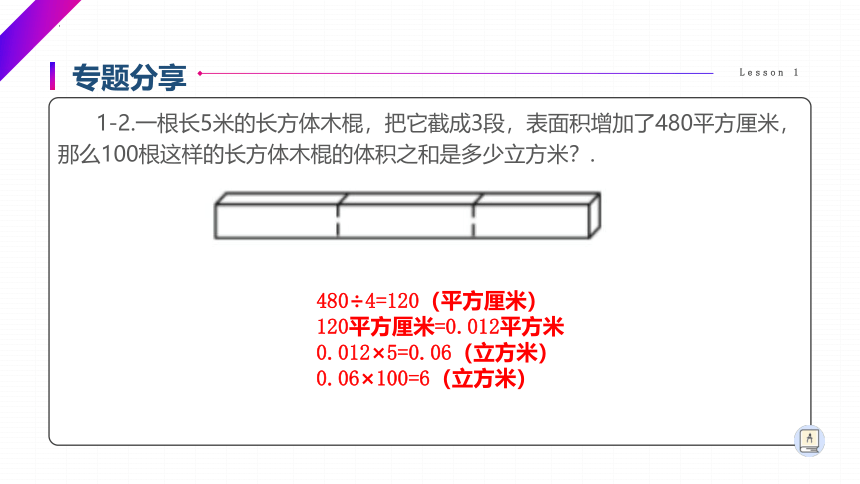
1-2.一根长5米的长方体木棍,把它截成3段,表面积增加了480平方厘米,那么100根这样的长方体木棍的体积之和是多少立方米?.
专题分享
480÷4=120(平方厘米)
120平方厘米=0.012平方米
0.012×5=0.06(立方米)
0.06×100=6(立方米)
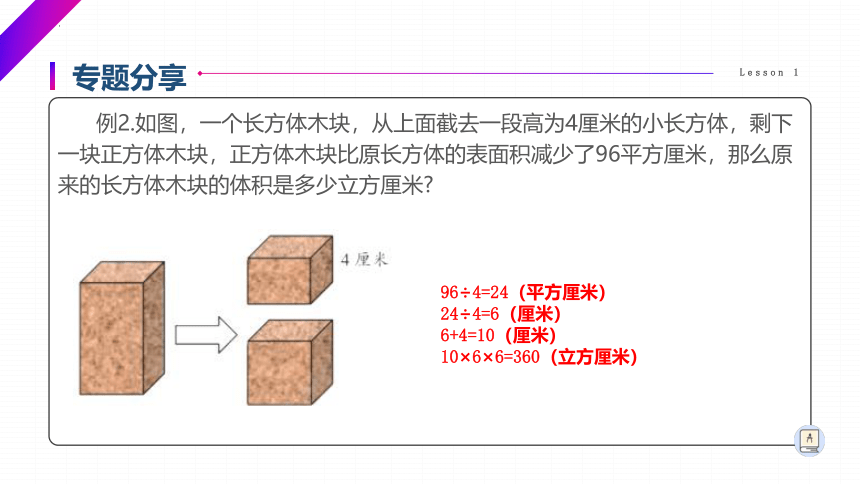
例2.如图,一个长方体木块,从上面截去一段高为4厘米的小长方体,剩下一块正方体木块,正方体木块比原长方体的表面积减少了96平方厘米,那么原来的长方体木块的体积是多少立方厘米
专题分享
96÷4=24(平方厘米)
24÷4=6(厘米)
6+4=10(厘米)
10×6×6=360(立方厘米)
练习2-1.如图,一个长方体木块,从上面截去一段高为5厘米的小长方体,剩下一块正方体木块,正方体木块比原长方体的表面积减少了60平方厘米,那么原来的长方体木块的体积是多少立方厘米
专题分享
每个面的面积为60÷4=15(平方厘米)
原长方体的长和宽都为15÷5=3(厘米)
原长方体的高为3+5=8(厘米)
长方体的体积是8×3×3=72(立方厘米)
2-2.如图,两根长度均为10米的长方体木棍粘合在一起,表面积减少了300平方厘米,那么粘合后的长方体木棍的体积是多少立方米
专题分享
一个横截面的面积为300÷2=150(平方厘米)
150平方厘米=0.015平方米
粘合后的长方体木棍的体积是0.015×10×2=0.3(立方米)
例3.已知一个正方体容器,棱长是20厘米,容器内的水面高度是8厘米,现在将一个长方体铁块完全浸没在水中,水面高度上升至11厘米,那么这个铁块的体积是多少立方厘米?
专题分享
水面上升的高度:11-8=3(厘米)
铁块的体积是:20×20×3=1200(立方厘米).
练习3-1.一个长方体玻璃缸,从里面量,长是35厘米,宽是20厘米,水深15厘米,当把一个土豆完全浸没在水中时,水的高度上升至16厘米(水未溢出),这个土豆的体积是多少立方厘米
专题分享
水面上升的高度:16一15=1(厘米)
土豆的体积是:35×20×1=700(立方厘米).
3-2.观察下面的图形,回答问题,
已知水池内每个小正方体的大小形状完全相同,球的大小形状也完全相同,且水均未溢出,请回答:
(1)这个水池的容积是( )立方厘米;
(2)每个小正方体的体积是( )立方厘米;
(3)球的体积是( ) 立方厘米;
(4)水池内水的体积是( )立方厘米,
专题分享
8400
280
840
6160
例4.有一个长方体容器,从里面量长12厘米,宽9厘米,高8厘米,里面注有一部分水,水深5厘米如果把一块棱长为6厘米的正方体铁块完全浸没在水中,水面会上升多少厘米
专题分享
铁块的体积是6×6×6=216(立方厘米)
水面上升的高度:216÷(12×9)=2(厘米)
练习4-1.有一个长方体容器,从里面量长5厘米,宽4厘米,高6厘米,里面注有一部分水,水深3厘米,如果把一块按长为2厘米的正方体铁块完全浸没在水中,水面会上升多少厘米
专题分享
铁块的体积是2×2×2=8(立方厘米)
水面上升的高度:8÷(5×4)=0.4(厘米)
4-2.一个长14分米,宽10分米,高8分米的玻璃容器,水面的高度是5分米,现在向容器中放入一个350立方分米的鹅卵石,并且完全浸没,现在水面的高度是多少分米?
专题分享
水上升的高度为350:14÷10=2.5(分米)
现在水面的高度是2.5+5=7.5(分米)
例5.在一个棱长为2.4分米的正方体水槽中装满水,现在将一个铅球完全浸没在水中,水槽中有一部分水溢出,再将铅球从水槽中取出,现在的水面高度是20厘米那么这个铅球的体积是多少立方分米?(不计损耗)
小心陷阱
20厘米=2分米
铅球的体积就是溢出水的体积为
2.4×2.4×(2.4-2)=2.304(立方分米)
课后巩固
3.
例1.如图,一个长方体木块,从上面截去一段高为6厘米的小长方体,剩下一块正方体木块,正方体木块比原长方体的表面积减少了168平方厘米,那么原来的长方体木块的体积是多少立方厘米?
课后巩固
每个面的面积为168÷4=42(平方厘米)
原长方体的长和宽都为42÷6=7(厘米)
原长方体的高为6+7=13(厘米)
长方体的体积是13×7×7=637(立方厘米)
例2.一个长方体鱼缸长是40分米,宽是10分米,水面的高度是2分米,放入1块鹅卵石完全浸没后,无水溢出,水面的高度变成2.5分米,那么鹅卵石的体积是多少立方分米?
课后巩固
鹅卵石的体积为40×10×(2.5一2)=200(立方厘米)
例3.一个长方体水槽的长、宽、高分别是15分米、10分米、6分米,水槽内水面的高度是3分米,现往水槽内投入一个铁块,铁块完全浸没在水中,水面上升到4分米,那么这个铁块的体积是多少平方分米?
课后巩固
铁块的体积为15×10×(4一3)=150(立方分米).
例4.观察下面的图形,回答问题:
已知水池内每个小正方体的大小形状完全相同,球的大小形状也完全相同,且水均未溢出,请回答:
(1)每个小正方体的体积是 ( )立方厘米;
(2)球的体积是( )立方厘米
课后巩固
25
50
例5.一个长5分米,宽3分米,高2分米的玻璃容器,水面的高度是0.8分米,现在向容器中放入一个1500立方厘米的石头,并且这块石头可以完全浸没,现在水面的高度是多少分米?
课后巩固
1500立方厘米=1.5立方分米
0.8+1.5(5×3)=0.9(分米)
专题附加
4.
挑战1. 一个长方体水缸,从里面量长8dm,宽6dm,高4dm,水深3.8dm,如果投入一块棱长为3dm的正方体铁块,缸里的水溢出多少升?
专题附加
正方体铁块的体积:3×3×3=27(dm)
长方体水缸除去水的体积:8×6×(4-3.8)=9.6(dm3)
溢出水的体积:27-9.6=17.4(dm3),
17.4立方分米=17.4升,则溢出17.4升.
再 见
祝同学们生活愉快!
长方体与正方体(四)
第 7 讲
专题解析
专题分享
课后巩固
专题附加
专题解析
1.
1.长方体的体积=长×宽×高 V=abh
2.正方体的体积=棱长×棱长×棱长 V=a×a×a = a3
3.*形状不规则的物体可以用排水法求体积,形状规则的物体可以用公式直接求体积。
排水法的公式:
V物体 =V现在-V原来
也可以 V物体 =S×(h现在- h原来)
V物体 =S×h升高
专题解析
专题分享
2.
例1.一根长6米的长方体木棍,把它截成3段,表面积增加了72平方米,那么1根这样的长方体木棍的体积是多少立方米?
专题分享
2÷4=18(平方米)
18×6=108(立方米)
练习1-1.如图,三根长度均为20米的长方体木棍粘合在一起,表面积减少了64平方米,那么粘合后的长方体木棍的体积是多少立方米
专题分享
64÷4=16(平方米)
16×20×3=960(立方米)
1-2.一根长5米的长方体木棍,把它截成3段,表面积增加了480平方厘米,那么100根这样的长方体木棍的体积之和是多少立方米?.
专题分享
480÷4=120(平方厘米)
120平方厘米=0.012平方米
0.012×5=0.06(立方米)
0.06×100=6(立方米)
例2.如图,一个长方体木块,从上面截去一段高为4厘米的小长方体,剩下一块正方体木块,正方体木块比原长方体的表面积减少了96平方厘米,那么原来的长方体木块的体积是多少立方厘米
专题分享
96÷4=24(平方厘米)
24÷4=6(厘米)
6+4=10(厘米)
10×6×6=360(立方厘米)
练习2-1.如图,一个长方体木块,从上面截去一段高为5厘米的小长方体,剩下一块正方体木块,正方体木块比原长方体的表面积减少了60平方厘米,那么原来的长方体木块的体积是多少立方厘米
专题分享
每个面的面积为60÷4=15(平方厘米)
原长方体的长和宽都为15÷5=3(厘米)
原长方体的高为3+5=8(厘米)
长方体的体积是8×3×3=72(立方厘米)
2-2.如图,两根长度均为10米的长方体木棍粘合在一起,表面积减少了300平方厘米,那么粘合后的长方体木棍的体积是多少立方米
专题分享
一个横截面的面积为300÷2=150(平方厘米)
150平方厘米=0.015平方米
粘合后的长方体木棍的体积是0.015×10×2=0.3(立方米)
例3.已知一个正方体容器,棱长是20厘米,容器内的水面高度是8厘米,现在将一个长方体铁块完全浸没在水中,水面高度上升至11厘米,那么这个铁块的体积是多少立方厘米?
专题分享
水面上升的高度:11-8=3(厘米)
铁块的体积是:20×20×3=1200(立方厘米).
练习3-1.一个长方体玻璃缸,从里面量,长是35厘米,宽是20厘米,水深15厘米,当把一个土豆完全浸没在水中时,水的高度上升至16厘米(水未溢出),这个土豆的体积是多少立方厘米
专题分享
水面上升的高度:16一15=1(厘米)
土豆的体积是:35×20×1=700(立方厘米).
3-2.观察下面的图形,回答问题,
已知水池内每个小正方体的大小形状完全相同,球的大小形状也完全相同,且水均未溢出,请回答:
(1)这个水池的容积是( )立方厘米;
(2)每个小正方体的体积是( )立方厘米;
(3)球的体积是( ) 立方厘米;
(4)水池内水的体积是( )立方厘米,
专题分享
8400
280
840
6160
例4.有一个长方体容器,从里面量长12厘米,宽9厘米,高8厘米,里面注有一部分水,水深5厘米如果把一块棱长为6厘米的正方体铁块完全浸没在水中,水面会上升多少厘米
专题分享
铁块的体积是6×6×6=216(立方厘米)
水面上升的高度:216÷(12×9)=2(厘米)
练习4-1.有一个长方体容器,从里面量长5厘米,宽4厘米,高6厘米,里面注有一部分水,水深3厘米,如果把一块按长为2厘米的正方体铁块完全浸没在水中,水面会上升多少厘米
专题分享
铁块的体积是2×2×2=8(立方厘米)
水面上升的高度:8÷(5×4)=0.4(厘米)
4-2.一个长14分米,宽10分米,高8分米的玻璃容器,水面的高度是5分米,现在向容器中放入一个350立方分米的鹅卵石,并且完全浸没,现在水面的高度是多少分米?
专题分享
水上升的高度为350:14÷10=2.5(分米)
现在水面的高度是2.5+5=7.5(分米)
例5.在一个棱长为2.4分米的正方体水槽中装满水,现在将一个铅球完全浸没在水中,水槽中有一部分水溢出,再将铅球从水槽中取出,现在的水面高度是20厘米那么这个铅球的体积是多少立方分米?(不计损耗)
小心陷阱
20厘米=2分米
铅球的体积就是溢出水的体积为
2.4×2.4×(2.4-2)=2.304(立方分米)
课后巩固
3.
例1.如图,一个长方体木块,从上面截去一段高为6厘米的小长方体,剩下一块正方体木块,正方体木块比原长方体的表面积减少了168平方厘米,那么原来的长方体木块的体积是多少立方厘米?
课后巩固
每个面的面积为168÷4=42(平方厘米)
原长方体的长和宽都为42÷6=7(厘米)
原长方体的高为6+7=13(厘米)
长方体的体积是13×7×7=637(立方厘米)
例2.一个长方体鱼缸长是40分米,宽是10分米,水面的高度是2分米,放入1块鹅卵石完全浸没后,无水溢出,水面的高度变成2.5分米,那么鹅卵石的体积是多少立方分米?
课后巩固
鹅卵石的体积为40×10×(2.5一2)=200(立方厘米)
例3.一个长方体水槽的长、宽、高分别是15分米、10分米、6分米,水槽内水面的高度是3分米,现往水槽内投入一个铁块,铁块完全浸没在水中,水面上升到4分米,那么这个铁块的体积是多少平方分米?
课后巩固
铁块的体积为15×10×(4一3)=150(立方分米).
例4.观察下面的图形,回答问题:
已知水池内每个小正方体的大小形状完全相同,球的大小形状也完全相同,且水均未溢出,请回答:
(1)每个小正方体的体积是 ( )立方厘米;
(2)球的体积是( )立方厘米
课后巩固
25
50
例5.一个长5分米,宽3分米,高2分米的玻璃容器,水面的高度是0.8分米,现在向容器中放入一个1500立方厘米的石头,并且这块石头可以完全浸没,现在水面的高度是多少分米?
课后巩固
1500立方厘米=1.5立方分米
0.8+1.5(5×3)=0.9(分米)
专题附加
4.
挑战1. 一个长方体水缸,从里面量长8dm,宽6dm,高4dm,水深3.8dm,如果投入一块棱长为3dm的正方体铁块,缸里的水溢出多少升?
专题附加
正方体铁块的体积:3×3×3=27(dm)
长方体水缸除去水的体积:8×6×(4-3.8)=9.6(dm3)
溢出水的体积:27-9.6=17.4(dm3),
17.4立方分米=17.4升,则溢出17.4升.
再 见
祝同学们生活愉快!
