数学人教A版(2019)必修第一册1.5全称量词与存在量词 课件(共17张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册1.5全称量词与存在量词 课件(共17张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 26.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-11 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
人教A版 必修第一册
第一章 集合与常用逻辑用语
1.5 全称量词与存在量词
一、创设情境,呈现目标
1.理解全称量词与存在量词的含义,熟悉常见的全称量词和存在量词.
2.了解含有量词的全称命题和存在命题的含义,并能用数学符号表示含有量词的命题及判断命题的真假性.
3.能正确地对含有一个量词的命题进行否定,理解全称命题与存在命题之间的关系.
二、问题预设,精讲点拨
1.什么是全称量词?常见的全称量词有哪些?怎样表示全称量词命题?
2.什么是存在量词?常见的存在量词有哪些?怎样表示存在量词命题?
1.全称量词与全称命题
(1)短语“所有的”“任意一个”在逻辑中通常叫做__________,并用符号“ ”表示.
(2)含有全称量词的命题,叫做__________________.
(3)全称命题的表述形式:对M中任意一个x,有p(x)成立,可简记为:___________,读作“对任意x属于M,有p(x)成立”.
(4)全称量词命题的真假判断:要判断一个全称命题量词是真命题,必须对限定集合M中的每一个元素x,验证p(x)成立;但要判断一个全称量词命题是假命题,只需列举出一个x0∈M,使得p(x0)不成立即可.
名师点拨常用的全称量词还有“所有”“每一个”“任何”“任意”“一切”“任给”“全部”.只要含有这些量词,或者命题具有全称量词所表达的含义,就是全称量词命题.
全称量词
全称量词命题
x∈M,p(x)
二、问题预设,精讲点拨
2.存在量词与存在量词命题
(1)短语“存在一个”“至少有一个”在逻辑中通常叫做_________,并用符号“ ”表示.
(2)含有存在量词的命题,叫做__________________.
(3)存在量词命题的表述形式:存在M中的一个x0,使p(x0)成立,可简记为_____________:,读作“存在M中的元素x0,使p(x0)成立”.
(4)存在量词命题的真假判断:要判断一个存在量词命题是真命题,只要在限定集合M中,能找到一个x0,使得命题p(x0)成立即可;否则这一命题就是假命题.
名师点拨常用的存在量词还有“有些”、“有一个”、“存在”、“某个”、“有的”等.只要含有这些量词,或者命题具有存在量词所表达的含义,就是存在量词命题.
全称量词
全称量词命题
x0∈M,p(x0)
二、问题预设,精讲点拨
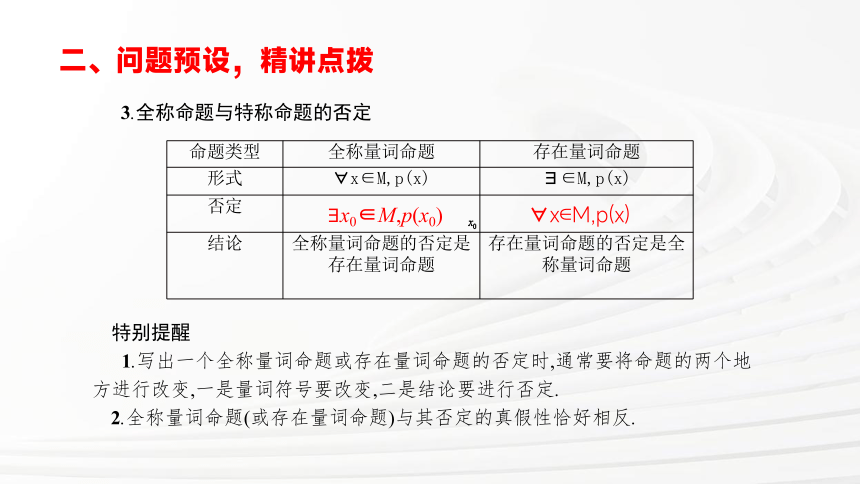
3.全称命题与特称命题的否定
特别提醒
1.写出一个全称量词命题或存在量词命题的否定时,通常要将命题的两个地方进行改变,一是量词符号要改变,二是结论要进行否定.
2.全称量词命题(或存在量词命题)与其否定的真假性恰好相反.
命题类型 全称量词命题 存在量词命题
形式 x∈M,p(x) ∈M,p(x)
否定
结论 全称量词命题的否定是存在量词命题 存在量词命题的否定是全称量词命题
x0∈M,p(x0)
x∈M,p(x)
二、问题预设,精讲点拨
三、自主内化,发现问题
阅读课本28-30页,思考并发现提出问题
要求:学生独立完成,以小组为单位,组内可商量,最终选出代表将问题写在小组对应的黑板区域内。
四,合作交流,解决问题
小组讨论黑板上各组提出的问题,并选出代表上黑板讲解。
各组根据自己组内提出的问题,分析判断其他组讲解是否正确全面、并做好随时补充的准备。
解题方法(判断一个命题是全称量词命题还是存在量词命题的方法)
(1)分析命题中所含的量词,含有全称量词的命题是全称量词命题,含有存在量词的命题是存在量词命题.
(2)当命题中不含量词时,要注意根据命题的含义进行判断.
(3)全称量词命题有时会省略全称量词,但存在量词命题的量词一般不能省略.
五,当堂训练,归纳延伸
解题方法(全称量词命题与存在量词命题真假的判断技巧)
(1)全称量词命题:要判定一个全称量词命题是真命题,必须对限定集合M中的每个元素x验证p(x)成立;但要判定全称量词 命题是假命题,只要能举出集合M中的一个x=x0,使得p(x0)不成立即可.
(2)存在量词命题:要判定一个存在量词命题是真命题,只要在限定集合M中,找到一个x=x0,使p(x0)成立即可;否则,这一存在量词命题就是假命题.
五,当堂训练,归纳延伸
解题方法(含有一个量词的命题的否定方法)
(1)一般地,写含有一个量词的命题的否定,首先要明确这个命题是全称量词命题还是存在量词命题,并找到其量词的位置及相应结论,然后把命题中的全称量词改成存在量词,存在量词改成全称量词,同时否定结论.
(2)对于省略量词的命题,应先挖掘命题中隐含的量词,改写成含量词的完整形式,再依据规则来写出命题的否定.
五,当堂训练,归纳延伸
2.写出下列命题的否定,并判断其真假:
(1)有些质数是奇数;
(2)菱形的对角线互相垂直;
(4)不论m取何实数,方程x2+2x-m=0都有实数根.
解析:(1)“有些质数是奇数”是特称命题,其否定为“所有质数都不是奇数”,它是假命题.
(2)“菱形的对角线互相垂直”是全称命题,其否定为“有的菱形的对角线不垂直”,它是假命题.
(4)“不论m取何实数,方程x2+2x-m=0都有实数根”是全称命题,其否定为“存在实数m0,使得方程x2+2x-m0=0没有实数根”,它是真命题.
本节课你学习了什么内容?
六,课堂小结
人教A版 必修第一册
第一章 集合与常用逻辑用语
1.5 全称量词与存在量词
一、创设情境,呈现目标
1.理解全称量词与存在量词的含义,熟悉常见的全称量词和存在量词.
2.了解含有量词的全称命题和存在命题的含义,并能用数学符号表示含有量词的命题及判断命题的真假性.
3.能正确地对含有一个量词的命题进行否定,理解全称命题与存在命题之间的关系.
二、问题预设,精讲点拨
1.什么是全称量词?常见的全称量词有哪些?怎样表示全称量词命题?
2.什么是存在量词?常见的存在量词有哪些?怎样表示存在量词命题?
1.全称量词与全称命题
(1)短语“所有的”“任意一个”在逻辑中通常叫做__________,并用符号“ ”表示.
(2)含有全称量词的命题,叫做__________________.
(3)全称命题的表述形式:对M中任意一个x,有p(x)成立,可简记为:___________,读作“对任意x属于M,有p(x)成立”.
(4)全称量词命题的真假判断:要判断一个全称命题量词是真命题,必须对限定集合M中的每一个元素x,验证p(x)成立;但要判断一个全称量词命题是假命题,只需列举出一个x0∈M,使得p(x0)不成立即可.
名师点拨常用的全称量词还有“所有”“每一个”“任何”“任意”“一切”“任给”“全部”.只要含有这些量词,或者命题具有全称量词所表达的含义,就是全称量词命题.
全称量词
全称量词命题
x∈M,p(x)
二、问题预设,精讲点拨
2.存在量词与存在量词命题
(1)短语“存在一个”“至少有一个”在逻辑中通常叫做_________,并用符号“ ”表示.
(2)含有存在量词的命题,叫做__________________.
(3)存在量词命题的表述形式:存在M中的一个x0,使p(x0)成立,可简记为_____________:,读作“存在M中的元素x0,使p(x0)成立”.
(4)存在量词命题的真假判断:要判断一个存在量词命题是真命题,只要在限定集合M中,能找到一个x0,使得命题p(x0)成立即可;否则这一命题就是假命题.
名师点拨常用的存在量词还有“有些”、“有一个”、“存在”、“某个”、“有的”等.只要含有这些量词,或者命题具有存在量词所表达的含义,就是存在量词命题.
全称量词
全称量词命题
x0∈M,p(x0)
二、问题预设,精讲点拨
3.全称命题与特称命题的否定
特别提醒
1.写出一个全称量词命题或存在量词命题的否定时,通常要将命题的两个地方进行改变,一是量词符号要改变,二是结论要进行否定.
2.全称量词命题(或存在量词命题)与其否定的真假性恰好相反.
命题类型 全称量词命题 存在量词命题
形式 x∈M,p(x) ∈M,p(x)
否定
结论 全称量词命题的否定是存在量词命题 存在量词命题的否定是全称量词命题
x0∈M,p(x0)
x∈M,p(x)
二、问题预设,精讲点拨
三、自主内化,发现问题
阅读课本28-30页,思考并发现提出问题
要求:学生独立完成,以小组为单位,组内可商量,最终选出代表将问题写在小组对应的黑板区域内。
四,合作交流,解决问题
小组讨论黑板上各组提出的问题,并选出代表上黑板讲解。
各组根据自己组内提出的问题,分析判断其他组讲解是否正确全面、并做好随时补充的准备。
解题方法(判断一个命题是全称量词命题还是存在量词命题的方法)
(1)分析命题中所含的量词,含有全称量词的命题是全称量词命题,含有存在量词的命题是存在量词命题.
(2)当命题中不含量词时,要注意根据命题的含义进行判断.
(3)全称量词命题有时会省略全称量词,但存在量词命题的量词一般不能省略.
五,当堂训练,归纳延伸
解题方法(全称量词命题与存在量词命题真假的判断技巧)
(1)全称量词命题:要判定一个全称量词命题是真命题,必须对限定集合M中的每个元素x验证p(x)成立;但要判定全称量词 命题是假命题,只要能举出集合M中的一个x=x0,使得p(x0)不成立即可.
(2)存在量词命题:要判定一个存在量词命题是真命题,只要在限定集合M中,找到一个x=x0,使p(x0)成立即可;否则,这一存在量词命题就是假命题.
五,当堂训练,归纳延伸
解题方法(含有一个量词的命题的否定方法)
(1)一般地,写含有一个量词的命题的否定,首先要明确这个命题是全称量词命题还是存在量词命题,并找到其量词的位置及相应结论,然后把命题中的全称量词改成存在量词,存在量词改成全称量词,同时否定结论.
(2)对于省略量词的命题,应先挖掘命题中隐含的量词,改写成含量词的完整形式,再依据规则来写出命题的否定.
五,当堂训练,归纳延伸
2.写出下列命题的否定,并判断其真假:
(1)有些质数是奇数;
(2)菱形的对角线互相垂直;
(4)不论m取何实数,方程x2+2x-m=0都有实数根.
解析:(1)“有些质数是奇数”是特称命题,其否定为“所有质数都不是奇数”,它是假命题.
(2)“菱形的对角线互相垂直”是全称命题,其否定为“有的菱形的对角线不垂直”,它是假命题.
(4)“不论m取何实数,方程x2+2x-m=0都有实数根”是全称命题,其否定为“存在实数m0,使得方程x2+2x-m0=0没有实数根”,它是真命题.
本节课你学习了什么内容?
六,课堂小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
