小升初分班考易错点真题检测卷(试题)数学六年级下册苏教版(含解析)
文档属性
| 名称 | 小升初分班考易错点真题检测卷(试题)数学六年级下册苏教版(含解析) | 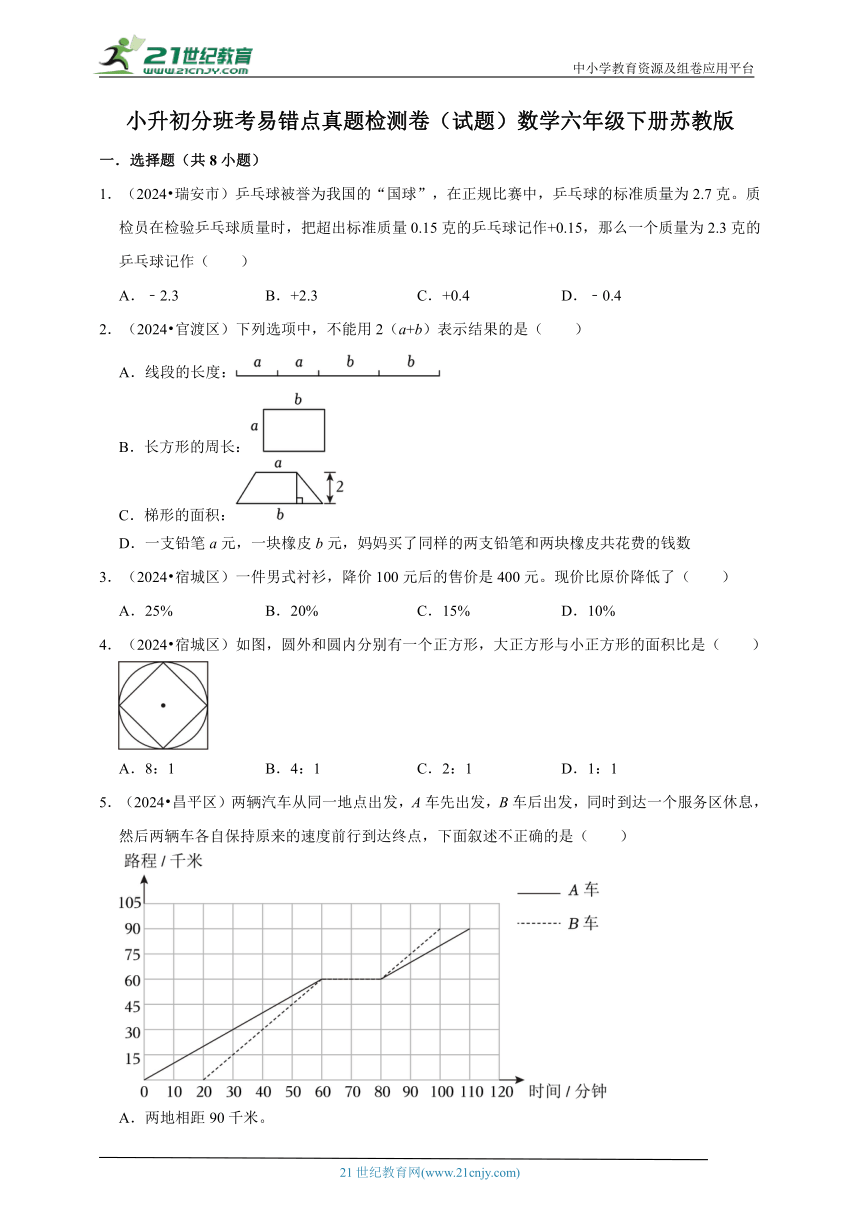 | |
| 格式 | doc | ||
| 文件大小 | 566.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-11 20:52:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
小升初分班考易错点真题检测卷(试题)数学六年级下册苏教版
一.选择题(共8小题)
1.(2024 瑞安市)乒乓球被誉为我国的“国球”,在正规比赛中,乒乓球的标准质量为2.7克。质检员在检验乒乓球质量时,把超出标准质量0.15克的乒乓球记作+0.15,那么一个质量为2.3克的乒乓球记作( )
A.﹣2.3 B.+2.3 C.+0.4 D.﹣0.4
2.(2024 官渡区)下列选项中,不能用2(a+b)表示结果的是( )
A.线段的长度:
B.长方形的周长:
C.梯形的面积:
D.一支铅笔a元,一块橡皮b元,妈妈买了同样的两支铅笔和两块橡皮共花费的钱数
3.(2024 宿城区)一件男式衬衫,降价100元后的售价是400元。现价比原价降低了( )
A.25% B.20% C.15% D.10%
4.(2024 宿城区)如图,圆外和圆内分别有一个正方形,大正方形与小正方形的面积比是( )
A.8:1 B.4:1 C.2:1 D.1:1
5.(2024 昌平区)两辆汽车从同一地点出发,A车先出发,B车后出发,同时到达一个服务区休息,然后两辆车各自保持原来的速度前行到达终点,下面叙述不正确的是( )
A.两地相距90千米。
B.两车休息时间为20分钟。
C.B车共用时80分钟。
D.A车的速度比B车的速度快。
6.(2024 慈溪市)已知a×1.2=b+=c÷=d﹣=1,则a,b,c,d中最小的数是( )
A.a B.b C.c D.d
7.(2024 仓山区)某商品售价60元,比原来定价便宜15%,求比原来定价便宜多少元?正确算式是( )
A.60÷(1﹣15%)﹣60 B.60÷(1﹣15%)
C.60÷(1+15%)﹣60 D.60×(1﹣15%)
8.(2023春 台江区期中)下面关于正比例和反比例的四个说法,正确的有( )
①正比例关系的图象是一条从(0,0)出发的无限延伸的射线
②一个人的年龄和体重既不成正比例关系,也不成反比例关系
③圆柱的底面积一定,它的体积和高成反比例关系
④路程一定,已走的路程和剩下的路程不成比例关系
A.①②③ B.①②④ C.②③④ D.①③④
二.填空题(共8小题)
9.(2024 江陵县)夏季是溺水高发期,防溺水安全记心间。某蓄水池的标准水位记作0米,正数表示高于标准水位的水面高度,那么高于标准水位1.5米,应该记作 米,低于标准水位1.8米,应该记作 米。
10.(2024 徐州)比40千克多是 千克: 千克比40千克少千克。
11.(2024 颍泉区)如果=y,那么x和y成 比例;如果14x=y,那么x和y成 比例。
12.(2024 江北区)做一份工作,已知甲单独完成该工作的所需时间与乙单独完成该工作的所需时间相等,那么甲乙工作效率之比是 。
13.(2024 开封)端午节,笑笑和妈妈用芦苇叶和糯米包近似圆锥形的粽子,底面直径为6厘米,高为5厘米。如果每立方厘米糯米重1.8克,包100个这样的粽子一共需要糯米 克。
14.(2024 江北区)用四根小棒搭成正方形,按规律依次摆下去,摆第5个需要 根小棒,摆n个需要 根小棒。
15.(2024 蜀山区)学校合唱团受邀参加合肥市文化艺术节开幕式活动,合唱团里,男生人数是女生人数的,男生人数比女生少,女生人数是合唱团总人数的 %。
16.(2024 永定区)在比例尺是1:10000000的地图上,量得甲地到乙地的距离是4.2厘米,甲地到乙地的实际距离是 千米,甲、乙两辆汽车同时从两地相对开出,甲车每小时行80千米,乙车的速度是甲车的75%,经过 小时两车相遇。
三.计算题(共4小题)
17.(2024 包河区)直接写得数。
612÷6= = 4.67+5.33= 78×0=
45×80%= 0.42= = =
18.(2024 江北区)下面各题,怎样算简便就怎样算。
46.7﹣19.13﹣6.87 1.25×2.5×3.2
35×12+350÷70 5
19.(2024 江北区)解方程。
2x+30%x=6.9
x
20.(2021 丹江口市)求阴影部分的面积。(单位:厘米)
四.应用题(共6小题)
21.(2024 锡山区)某市地铁1号线地下总长27.35千米,比地上总长的3倍还多5.6千米。该市地铁1号线地上总长多少千米?
22.(2024 项城市)保护家园,人人有责。前进小学开展“做讲卫生小卫士”活动,六年级男同学收废纸20kg,比女同学少收。六年级同学一共收废纸多少千克?
23.(2024 项城市)有两筐梨,甲筐梨的质量是32kg,从乙筐取出20%后,甲、乙两筐梨的质量比是4:3。原来甲、乙两筐梨共有多少千克?
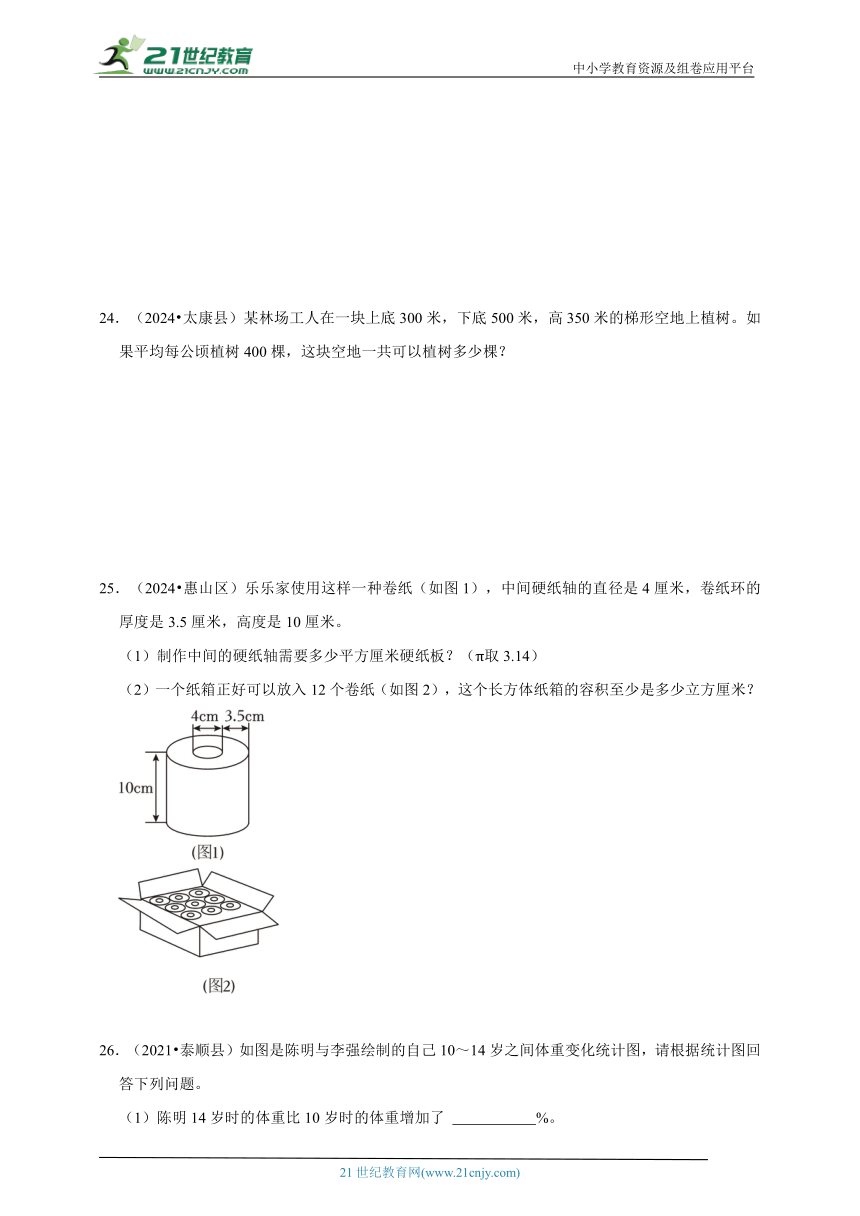
24.(2024 太康县)某林场工人在一块上底300米,下底500米,高350米的梯形空地上植树。如果平均每公顷植树400棵,这块空地一共可以植树多少棵?
25.(2024 惠山区)乐乐家使用这样一种卷纸(如图1),中间硬纸轴的直径是4厘米,卷纸环的厚度是3.5厘米,高度是10厘米。
(1)制作中间的硬纸轴需要多少平方厘米硬纸板?(π取3.14)
(2)一个纸箱正好可以放入12个卷纸(如图2),这个长方体纸箱的容积至少是多少立方厘米?
26.(2021 泰顺县)如图是陈明与李强绘制的自己10~14岁之间体重变化统计图,请根据统计图回答下列问题。
(1)陈明14岁时的体重比10岁时的体重增加了 %。
(2)周宏说:“表示陈明体重变化的折线倾斜度较大,所以陈明的体重增长较快。”你认为她说的是否正确?简要说明理由。
小升初分班考易错点真题检测卷(试题)数学六年级下册苏教版
参考答案与试题解析
一.选择题(共8小题)
1.【分析】在用正、负数表示两种具有相反意义的量时,要先规定哪种量为正(或负)。如果一种量用正数表示,那么另一种与它相反的量就用负数表示。据此解答即可。
【解答】解:把一个超出标准质量0.15克的乒乓球记作+0.15,那么一个质量为2.3克的乒乓球记作2.3﹣2.7=﹣0.4(克)。
故选:D。
【点评】在用正、负数表示两种具有相反意义的量时,一般用正数表示增加、上升、超出……用负数表示减少、下降、不足……
2.【分析】A.从图中可知,线段的长度是2个a与2个b的和;
B.根据“长方形的周长=(长+宽)×2”解答;
C.根据“梯形的面积=(上底+下底)×高÷2”解答;
D.根据“单价×数量=总价”可得数量关系:铅笔的单价×铅笔的数量+橡皮的单价×橡皮的数量=买铅笔和橡皮的总花费;
根据数量关系找出不能用2(a+b)表示结果的选项即可。
【解答】A.线段的长度:2a+2b=2(a+b);能用2(a+b)表示结果,不符合题意;
B.长方形的周长:2(a+b);能用2(a+b)表示结果,不符合题意;
C.梯形的面积:(a+b)×2÷2=a+b;不能用2(a+b)表示结果,符合题意;
D.共花费的钱数:2a+2b=2(a+b);能用2(a+b)表示结果,不符合题意。
所以C选项不能用2(a+b)表示。
故选:C。
【点评】本题考查用字母表示式子,根据线段图、长方形的周长公式、梯形的面积公式、单价、数量与总价之间的关系,得出数量关系,按数量关系写出含字母的式子。
3.【分析】一件男式衬衫,降价100元后的售价是400元,则原价是(400+100)元。求现价比原价降低了百分之几,用100元除以原价。
【解答】解:100÷(400+100)
=100÷500
=0.2
=20%
答:现价比原价降低了20%。
故选:B。
【点评】求一个数是另一个数的几分之几,用这两数之差除以另一个数。
4.【分析】设圆的直径是d,则大正方形的边长是d,小正方形的对角线为d,根据“正方形的面积=边长×边长”,“正方形的面积=对角线×对角线×”进行分别计算出大正方形的面积和小正方形的面积,最后写出比。
【解答】解:根据分析,设圆的半径是d,则大正方形的边长是d,小正方形的对角线为d;
则大正方形的面积为:d×d=d2
小正方形的面积为:d×d×=d2
则大正方形与小正方形的面积比为:d2:d2=2:1。
故选:C。
【点评】解答此题的关键是先根据正方形的面积计算公式,分别计算出大正方形的面积和小正方形的面积。
5.【分析】由图可知,两地相距90千米,A车从出发到到达目的地用了110分钟,中间休息了20分钟,所以行驶时间为(110﹣20)分钟,根据“速度=路程÷时间”,代入数据可求出A车的速度;B车从出发到到达目的地用了(100﹣20)分钟,中间休息了20分钟,所以行驶时间为(100﹣20﹣20)分钟,根据“速度=路程÷时间”,代入数据可求出B车的速度;据此对这四个选项逐一分析即可解答。
【解答】解:A.两地相距90千米。原题说法正确,不符合题意;
B.80﹣60=20(分钟),两车休息时间为20分钟。原题说法正确,不符合题意;
C.100﹣20=80(分钟),B车共用时80分钟。说原题法正确,不符合题意;
D.A车的速度:90÷(110﹣20)=1(千米/分)
B车的速度:90÷(100﹣20﹣20)=1.5(千米/分)
1<1.5,所以A车的速度比B车的速度慢。原题说法错误,符合题意。
故选:D。
【点评】解答本题的关键是先从图中找到关键信息,再利用路程、速度、时间之间的关系式进行计算。
6.【分析】本题有加减乘除法四个算式,四个算式的得数都等于1,根据加减乘除法各部分之间的关系求出a、b、c、d,再比较大小。
【解答】解:已知a×1.2=b+=c÷=d﹣=1
即a×1.2=1,则a=
b+=1,则b=
c÷=1,则c=
d﹣=1,则d=
因为>>>,所以d>a>c>b。
故选:B。
【点评】本题考查了分数大小比较的方法,解答的关键是四个算式的得数都等于1,求出a、b、c、d的值。
7.【分析】把原价看成单位“1”,现价是原价的(1﹣15%),它对应的数量是60元,由此用除法求出原价,再用原价减去现价就是便宜了多少钱.
【解答】解:原价表示为:
60÷(1﹣15%),
便宜的钱数就是60÷(1﹣85%)﹣60.
故选:A.
【点评】本题的关键是找出单位“1”,并找出单位“1”的百分之几对应的数量,用除法就可以求出单位“1”的量.
8.【分析】对于①,两种相关联的量的商一定时,它们成正比例关系,确定正比例关系的图象的特点;
对于②,人的体重与年龄不是相关联的量,体重随着年龄的增长可能增加、不变或者减少;
对于③,由圆柱的体积公式可知“圆柱的体积÷高=底面积(一定)”,据此判断说法的正误;
对于④,路程一定时,已走的路程与剩下的路程的和一定,据此判断说法的正误。
【解答】解:①正比例关系的图象是一条从(0,0)出发的无限延伸的射线,所以原题说法正确;
②一个人的年龄和体重既不成正比例关系,也不成反比例关系,所以原题说法正确;
③圆柱的体积÷高=底面积(一定),则圆柱的底面积一定,它的体积和高成正比例关系,所以原题说法错误;
④已走的路程+剩下的路程=总路程,则已走的路程和剩下的路程不成比例,所以原题说法正确。
综上可知,①②④正确。
故选:B。
【点评】本题关键是掌握两个相关联的量,如果两个数的比值一定,这两个量成正比例关系,如果两个量的乘积一定,这两个量成反比例关系。
二.填空题(共8小题)
9.【分析】根据题意,高于标准水位1.5米,应该记作1.5米,低于标准水位1.8米,应该记作﹣1.8米。
【解答】解:某蓄水池的标准水位记作0米,正数表示高于标准水位的水面高度,那么高于标准水位1.5米,应该记作1.5米,低于标准水位1.8米,应该记作﹣1.8米。
故答案为:1.5,﹣1.8。
【点评】此题考查了负数的意义及其应用,要求学生掌握。
10.【分析】把40千克看作单位“1”,则未知的质量是40千克的(1),根据分数乘法的意义,即可计算出未知的质量。
用40千克直接减去千克,即可计算出比40千克少千克是多少千克。
【解答】解:
=40×
=48(千克)
40=39.8(千克)
答:比40千克多是48千克:39.8千克比40千克少千克。
故答案为:48;39.8。
【点评】本题解题的关键是根据分数乘法的意义与分数减法的意义,列式计算。
11.【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【解答】解:如果=y,则xy=6,x和y的乘积一定,那么x和y成反比例;
如果14x=y,则x÷y=,x和y的比值一定,那么x和y成正比例。
故答案为:反;正。
【点评】掌握正、反比例的辨识是解答本题的关键。
12.【分析】根据工作时间一定,工作量和工作效率成正比例,可知甲与乙工作效率的比是:,再化简即可解答。
【解答】解::
=(×12):(×12)
=3:2
答:甲乙工作效率之比是3:2。
故答案为:3:2。
【点评】本题的关键是根据工作时间一定,工作量和工作效率成正比例,求出甲乙两人工作效率的比。
13.【分析】根据圆锥的体积公式:V=πr2h,把数据代入公式求出一个粽子的体积,然后用一个粽子的体积乘每立方厘米糯米的质量,再乘粽子的个数即可。
【解答】解:×3.14×(6÷2)2×5×1.8×100
=×3.14×9×5×1.8×100
=3.14×3×5×1.8×100
=9.42×5×1.8×100
=47.1×1.8×100
=84.78×100
=8478(克)
答:包100个这样的粽子需要糯米8478克。
故答案为:8478。
【点评】此题主要考查圆锥体积公式的灵活运用,关键是熟记公式。
14.【分析】由图可知,从第二个图形开始,每增加一个正方形,就会增加3根小棒;摆2个正方形,需要[4+(2﹣1)×3]根小棒;摆2个正方形,需要[4+(3﹣1)×3]根小棒……;据此规律解答。
【解答】解:4+(5﹣1)×3
=4+12
=16(根)
4+(n﹣1)×3
=4+3n﹣3
=(3n+1)(根)
答:摆第5个需要16根小棒,摆n个需要(3n+1)根小棒。
故答案为:16;(3n+1)。
【点评】解答本题需准确分析搭成的正方形个数与需要的小棒根数之间的关系,灵活找规律解答。
15.【分析】把女生人数看作单位“1”,则男生人数是,合唱团总人数是(1+)。求男生人数比女生少几分之几,用男、女生人数之差除以女生人数;求女生人数是合唱团总人数的百分之几,用女生人数除以合唱团总人数。
【解答】解:(1﹣)÷1
=÷1
=
1÷(1+)
=1÷
=0.625
=62.5%
答:男生人数比女生少,女生人数是合唱团总人数的62.5%。
故答案为:,62.5。
【点评】求一个数比另一个数多或少几分之几,用这两数之差除以另一个数;求一个数是另一个数的百分之几,用这个数除以另一个数。
16.【分析】根据图上距离÷比例尺=实际距离,列式求得甲、乙两地的实际距离,再根据“乙车的速度是甲车的75%,”知道75%的单位“1”是甲车的速度,根据分数乘法的意义求出乙车的速度,再根据路程÷速度和=相遇时间,列式解答即可。
【解答】解:4.2÷=42000000(厘米)
42000000厘米=420千米
420÷(80+80×75%)
=420÷(80+60)
=420÷140
=3(小时)
答:甲地到乙地的实际距离是420千米,经过3小时两车相遇。
故答案为:420,3。
【点评】此题主要考查比例尺、图上距离、实际距离三者之间的数量关系及速度,路程与时间的数量关系。
三.计算题(共4小题)
17.【分析】根据三位数除以一位数、小数加法、分数的加减乘除法、小数加法的计算方法以及0、乘方、百分数的运算计算即可。
【解答】解:
612÷6=102 = 4.67+5.33=10 78×0=0
45×80%=36 0.42=0.16 = =
【点评】熟练掌握三位数除以一位数、小数加法、分数的加减乘除法、小数加法的计算方法以及0、乘方、百分数的运算,是解答本题的关键。
18.【分析】按照减法的性质计算;
把3.2看成0.8×4,再按照乘法交换律和结合律计算;
按照乘法分配律计算;
先算乘法和除法,再算加法;
先算小括号里面的加法,再算除法;
先算小括号里面的加法,再算中括号里面的乘法,最后算除法。
【解答】解:46.7﹣19.13﹣6.87
=46.7﹣(19.13+6.87)
=46.7﹣26
=20.7
1.25×2.5×3.2
=(1.25×0.8)×(4×2.5)
=1×10
=10
=×(+)
=×2
=
35×12+350÷70
=420+5
=425
=22÷
=60
5
=5÷[×]
=5÷
=75
【点评】本题考查了四则混合运算,注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
19.【分析】第一题:在方程两边同时乘即可求出解;
第二题:首先在方程两边同时减去1,然后在方程两边同时除以即可求出解;
第三题:先将方程左边化简,然后在方程两边同时除以(2+30%)的和即可求出解;
第四题:先根据比例的基本性质将比例写成方程的形式,再根据解方程的方法求出解。
【解答】解:
x÷=
x=
x=12﹣1
x=11
x=11÷
x=55
2x+30%x=6.9
2.3x=6.9
x=6.9÷2.3
x=3
x
x=25×4
x=100
x=100÷
x=150
【点评】此题考查解方程和解比例。掌握比例的基性质和等式的性质是解答的关键。
20.【分析】如图,把半圆上的三个点分别命名为点A、点B、点C,由弧AC与弦AC围的阴影部分绕点O顺时针旋转90°后,同由弧BC与弦BC围成的图形重合,阴影部分则合成一个梯形,这个梯形的上底与圆的半径相等,下底是8厘米,高与圆的半径相等,根据“梯形面积=(上底+下底)×高÷2”即可算阴影部分的面积。
【解答】解:(6+8)×6÷2
=14×6÷2
=84÷2
=42(平方厘米)
答:阴影部分的面积为42平方厘米。
【点评】此题重点考查把不规则的阴影部分通过割拼法组合为规则图形再求面积的方法。
四.应用题(共6小题)
21.【分析】用地下总长减去地下总长比地上总长的3倍还多的5.6千米,用求得的差除以3即可求出该市地铁1号线地上总长。
【解答】解:(27.35﹣5.6)÷3
=21.75÷3
=7.25(千米)
答:该市地铁1号线地上总长7.25千米。
【点评】解答此题的关键是理清数量关系,再列式计算。
22.【分析】把女同学收废纸的千克数看作单位“1”,用女同学收废纸的千克数除以对应的分率(1﹣),求出女同学收废纸的千克数,再加男同学收废纸的千克数即可。
【解答】解:20÷(1﹣)+20
=20÷+20
=25+20
=45(千克)
答:六年级同学一共收废纸45千克。
【点评】本题主要考查了分数除法应用题,解题的关键是明确:已知一个数的几分之几是多少,求这个数,用除法计算。
23.【分析】先求出从乙筐取出20%后乙筐梨占甲筐梨的分率,然后将甲筐梨的质量看作单位“1”,用32千克乘所得的分率,求出乙筐梨取出20%后的质量;再除以(1﹣20%),可求出乙筐梨原有的质量,最后与甲筐梨的质量相加即可。
【解答】解:3÷4=
32×÷(1﹣20%)
=24÷80%
=30(千克)
32+30=62(千克)
答:原来甲、乙两筐梨共有62千克。
【点评】本题考查了利用比的知识、分数及百分数乘除混合运算解决问题,需准确分析题目中的数量关系。
24.【分析】根据梯形面积=(上底+下底)×高÷2求出梯形面积,把得数单位平方米换算成公顷,再乘400棵即可解答。
【解答】解:(300+500)×350÷2
=800×350÷2
=280000÷2
=140000(平方米)
140000平方米=14公顷
14×400=5600(棵)
答:这块空地一共可以植树5600棵。
【点评】本题考查的是梯形面积,熟记公式是解答关键。
25.【分析】(1)根据圆柱的侧面积公式:S=πdh,把数据代入公式解答。
(2)通过观察图形可知,纸箱的长等于纸卷底面直径的4倍,宽等于纸卷底面直径的3倍,高等于纸卷的高,根据长方体的容积公式:V=abh,把数据代入公式解答。
【解答】解:(1)3.14×4×10
=12.56×10
=125.6(平方厘米)
答:制作中间的硬纸轴需要125.6平方厘米硬纸板。
(2)4+3.5×2
=4+7
=11(厘米)
(11×4)×(11×3)×10
=44×33×10
=1452×10
=14520(立方厘米)
答:这个长方形纸箱的容积是14520立方厘米。
【点评】此题主要考查圆柱的侧面积公式、长方体的容积公式的灵活运用,关键是熟记公式。
26.【分析】(1)用陈明14岁时的体重减10岁时的体重,再除以10岁时的体重即可。
(2)陈明体重变化的折线纵轴上一格表示2千克,李强体重变化的折线纵轴上一格表示5千克,所以不能根据倾斜度来看体重增长快慢。
【解答】解:(1)(50﹣30)÷30
=20÷30
≈66.7%
答:陈明14岁时的体重比10岁时的体重增加了66.7%。
(2)她说的不正确,陈明体重变化的折线纵轴上一格表示2千克,李强体重变化的折线纵轴上一格表示5千克,所以不能根据倾斜度来看体重增长快慢。
故答案为:66.7。
【点评】本题是复式折线统计图,要通过坐标轴以及图例等读懂本图,根据图中所示的数量解决问题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
小升初分班考易错点真题检测卷(试题)数学六年级下册苏教版
一.选择题(共8小题)
1.(2024 瑞安市)乒乓球被誉为我国的“国球”,在正规比赛中,乒乓球的标准质量为2.7克。质检员在检验乒乓球质量时,把超出标准质量0.15克的乒乓球记作+0.15,那么一个质量为2.3克的乒乓球记作( )
A.﹣2.3 B.+2.3 C.+0.4 D.﹣0.4
2.(2024 官渡区)下列选项中,不能用2(a+b)表示结果的是( )
A.线段的长度:
B.长方形的周长:
C.梯形的面积:
D.一支铅笔a元,一块橡皮b元,妈妈买了同样的两支铅笔和两块橡皮共花费的钱数
3.(2024 宿城区)一件男式衬衫,降价100元后的售价是400元。现价比原价降低了( )
A.25% B.20% C.15% D.10%
4.(2024 宿城区)如图,圆外和圆内分别有一个正方形,大正方形与小正方形的面积比是( )
A.8:1 B.4:1 C.2:1 D.1:1
5.(2024 昌平区)两辆汽车从同一地点出发,A车先出发,B车后出发,同时到达一个服务区休息,然后两辆车各自保持原来的速度前行到达终点,下面叙述不正确的是( )
A.两地相距90千米。
B.两车休息时间为20分钟。
C.B车共用时80分钟。
D.A车的速度比B车的速度快。
6.(2024 慈溪市)已知a×1.2=b+=c÷=d﹣=1,则a,b,c,d中最小的数是( )
A.a B.b C.c D.d
7.(2024 仓山区)某商品售价60元,比原来定价便宜15%,求比原来定价便宜多少元?正确算式是( )
A.60÷(1﹣15%)﹣60 B.60÷(1﹣15%)
C.60÷(1+15%)﹣60 D.60×(1﹣15%)
8.(2023春 台江区期中)下面关于正比例和反比例的四个说法,正确的有( )
①正比例关系的图象是一条从(0,0)出发的无限延伸的射线
②一个人的年龄和体重既不成正比例关系,也不成反比例关系
③圆柱的底面积一定,它的体积和高成反比例关系
④路程一定,已走的路程和剩下的路程不成比例关系
A.①②③ B.①②④ C.②③④ D.①③④
二.填空题(共8小题)
9.(2024 江陵县)夏季是溺水高发期,防溺水安全记心间。某蓄水池的标准水位记作0米,正数表示高于标准水位的水面高度,那么高于标准水位1.5米,应该记作 米,低于标准水位1.8米,应该记作 米。
10.(2024 徐州)比40千克多是 千克: 千克比40千克少千克。
11.(2024 颍泉区)如果=y,那么x和y成 比例;如果14x=y,那么x和y成 比例。
12.(2024 江北区)做一份工作,已知甲单独完成该工作的所需时间与乙单独完成该工作的所需时间相等,那么甲乙工作效率之比是 。
13.(2024 开封)端午节,笑笑和妈妈用芦苇叶和糯米包近似圆锥形的粽子,底面直径为6厘米,高为5厘米。如果每立方厘米糯米重1.8克,包100个这样的粽子一共需要糯米 克。
14.(2024 江北区)用四根小棒搭成正方形,按规律依次摆下去,摆第5个需要 根小棒,摆n个需要 根小棒。
15.(2024 蜀山区)学校合唱团受邀参加合肥市文化艺术节开幕式活动,合唱团里,男生人数是女生人数的,男生人数比女生少,女生人数是合唱团总人数的 %。
16.(2024 永定区)在比例尺是1:10000000的地图上,量得甲地到乙地的距离是4.2厘米,甲地到乙地的实际距离是 千米,甲、乙两辆汽车同时从两地相对开出,甲车每小时行80千米,乙车的速度是甲车的75%,经过 小时两车相遇。
三.计算题(共4小题)
17.(2024 包河区)直接写得数。
612÷6= = 4.67+5.33= 78×0=
45×80%= 0.42= = =
18.(2024 江北区)下面各题,怎样算简便就怎样算。
46.7﹣19.13﹣6.87 1.25×2.5×3.2
35×12+350÷70 5
19.(2024 江北区)解方程。
2x+30%x=6.9
x
20.(2021 丹江口市)求阴影部分的面积。(单位:厘米)
四.应用题(共6小题)
21.(2024 锡山区)某市地铁1号线地下总长27.35千米,比地上总长的3倍还多5.6千米。该市地铁1号线地上总长多少千米?
22.(2024 项城市)保护家园,人人有责。前进小学开展“做讲卫生小卫士”活动,六年级男同学收废纸20kg,比女同学少收。六年级同学一共收废纸多少千克?
23.(2024 项城市)有两筐梨,甲筐梨的质量是32kg,从乙筐取出20%后,甲、乙两筐梨的质量比是4:3。原来甲、乙两筐梨共有多少千克?
24.(2024 太康县)某林场工人在一块上底300米,下底500米,高350米的梯形空地上植树。如果平均每公顷植树400棵,这块空地一共可以植树多少棵?
25.(2024 惠山区)乐乐家使用这样一种卷纸(如图1),中间硬纸轴的直径是4厘米,卷纸环的厚度是3.5厘米,高度是10厘米。
(1)制作中间的硬纸轴需要多少平方厘米硬纸板?(π取3.14)
(2)一个纸箱正好可以放入12个卷纸(如图2),这个长方体纸箱的容积至少是多少立方厘米?
26.(2021 泰顺县)如图是陈明与李强绘制的自己10~14岁之间体重变化统计图,请根据统计图回答下列问题。
(1)陈明14岁时的体重比10岁时的体重增加了 %。
(2)周宏说:“表示陈明体重变化的折线倾斜度较大,所以陈明的体重增长较快。”你认为她说的是否正确?简要说明理由。
小升初分班考易错点真题检测卷(试题)数学六年级下册苏教版
参考答案与试题解析
一.选择题(共8小题)
1.【分析】在用正、负数表示两种具有相反意义的量时,要先规定哪种量为正(或负)。如果一种量用正数表示,那么另一种与它相反的量就用负数表示。据此解答即可。
【解答】解:把一个超出标准质量0.15克的乒乓球记作+0.15,那么一个质量为2.3克的乒乓球记作2.3﹣2.7=﹣0.4(克)。
故选:D。
【点评】在用正、负数表示两种具有相反意义的量时,一般用正数表示增加、上升、超出……用负数表示减少、下降、不足……
2.【分析】A.从图中可知,线段的长度是2个a与2个b的和;
B.根据“长方形的周长=(长+宽)×2”解答;
C.根据“梯形的面积=(上底+下底)×高÷2”解答;
D.根据“单价×数量=总价”可得数量关系:铅笔的单价×铅笔的数量+橡皮的单价×橡皮的数量=买铅笔和橡皮的总花费;
根据数量关系找出不能用2(a+b)表示结果的选项即可。
【解答】A.线段的长度:2a+2b=2(a+b);能用2(a+b)表示结果,不符合题意;
B.长方形的周长:2(a+b);能用2(a+b)表示结果,不符合题意;
C.梯形的面积:(a+b)×2÷2=a+b;不能用2(a+b)表示结果,符合题意;
D.共花费的钱数:2a+2b=2(a+b);能用2(a+b)表示结果,不符合题意。
所以C选项不能用2(a+b)表示。
故选:C。
【点评】本题考查用字母表示式子,根据线段图、长方形的周长公式、梯形的面积公式、单价、数量与总价之间的关系,得出数量关系,按数量关系写出含字母的式子。
3.【分析】一件男式衬衫,降价100元后的售价是400元,则原价是(400+100)元。求现价比原价降低了百分之几,用100元除以原价。
【解答】解:100÷(400+100)
=100÷500
=0.2
=20%
答:现价比原价降低了20%。
故选:B。
【点评】求一个数是另一个数的几分之几,用这两数之差除以另一个数。
4.【分析】设圆的直径是d,则大正方形的边长是d,小正方形的对角线为d,根据“正方形的面积=边长×边长”,“正方形的面积=对角线×对角线×”进行分别计算出大正方形的面积和小正方形的面积,最后写出比。
【解答】解:根据分析,设圆的半径是d,则大正方形的边长是d,小正方形的对角线为d;
则大正方形的面积为:d×d=d2
小正方形的面积为:d×d×=d2
则大正方形与小正方形的面积比为:d2:d2=2:1。
故选:C。
【点评】解答此题的关键是先根据正方形的面积计算公式,分别计算出大正方形的面积和小正方形的面积。
5.【分析】由图可知,两地相距90千米,A车从出发到到达目的地用了110分钟,中间休息了20分钟,所以行驶时间为(110﹣20)分钟,根据“速度=路程÷时间”,代入数据可求出A车的速度;B车从出发到到达目的地用了(100﹣20)分钟,中间休息了20分钟,所以行驶时间为(100﹣20﹣20)分钟,根据“速度=路程÷时间”,代入数据可求出B车的速度;据此对这四个选项逐一分析即可解答。
【解答】解:A.两地相距90千米。原题说法正确,不符合题意;
B.80﹣60=20(分钟),两车休息时间为20分钟。原题说法正确,不符合题意;
C.100﹣20=80(分钟),B车共用时80分钟。说原题法正确,不符合题意;
D.A车的速度:90÷(110﹣20)=1(千米/分)
B车的速度:90÷(100﹣20﹣20)=1.5(千米/分)
1<1.5,所以A车的速度比B车的速度慢。原题说法错误,符合题意。
故选:D。
【点评】解答本题的关键是先从图中找到关键信息,再利用路程、速度、时间之间的关系式进行计算。
6.【分析】本题有加减乘除法四个算式,四个算式的得数都等于1,根据加减乘除法各部分之间的关系求出a、b、c、d,再比较大小。
【解答】解:已知a×1.2=b+=c÷=d﹣=1
即a×1.2=1,则a=
b+=1,则b=
c÷=1,则c=
d﹣=1,则d=
因为>>>,所以d>a>c>b。
故选:B。
【点评】本题考查了分数大小比较的方法,解答的关键是四个算式的得数都等于1,求出a、b、c、d的值。
7.【分析】把原价看成单位“1”,现价是原价的(1﹣15%),它对应的数量是60元,由此用除法求出原价,再用原价减去现价就是便宜了多少钱.
【解答】解:原价表示为:
60÷(1﹣15%),
便宜的钱数就是60÷(1﹣85%)﹣60.
故选:A.
【点评】本题的关键是找出单位“1”,并找出单位“1”的百分之几对应的数量,用除法就可以求出单位“1”的量.
8.【分析】对于①,两种相关联的量的商一定时,它们成正比例关系,确定正比例关系的图象的特点;
对于②,人的体重与年龄不是相关联的量,体重随着年龄的增长可能增加、不变或者减少;
对于③,由圆柱的体积公式可知“圆柱的体积÷高=底面积(一定)”,据此判断说法的正误;
对于④,路程一定时,已走的路程与剩下的路程的和一定,据此判断说法的正误。
【解答】解:①正比例关系的图象是一条从(0,0)出发的无限延伸的射线,所以原题说法正确;
②一个人的年龄和体重既不成正比例关系,也不成反比例关系,所以原题说法正确;
③圆柱的体积÷高=底面积(一定),则圆柱的底面积一定,它的体积和高成正比例关系,所以原题说法错误;
④已走的路程+剩下的路程=总路程,则已走的路程和剩下的路程不成比例,所以原题说法正确。
综上可知,①②④正确。
故选:B。
【点评】本题关键是掌握两个相关联的量,如果两个数的比值一定,这两个量成正比例关系,如果两个量的乘积一定,这两个量成反比例关系。
二.填空题(共8小题)
9.【分析】根据题意,高于标准水位1.5米,应该记作1.5米,低于标准水位1.8米,应该记作﹣1.8米。
【解答】解:某蓄水池的标准水位记作0米,正数表示高于标准水位的水面高度,那么高于标准水位1.5米,应该记作1.5米,低于标准水位1.8米,应该记作﹣1.8米。
故答案为:1.5,﹣1.8。
【点评】此题考查了负数的意义及其应用,要求学生掌握。
10.【分析】把40千克看作单位“1”,则未知的质量是40千克的(1),根据分数乘法的意义,即可计算出未知的质量。
用40千克直接减去千克,即可计算出比40千克少千克是多少千克。
【解答】解:
=40×
=48(千克)
40=39.8(千克)
答:比40千克多是48千克:39.8千克比40千克少千克。
故答案为:48;39.8。
【点评】本题解题的关键是根据分数乘法的意义与分数减法的意义,列式计算。
11.【分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【解答】解:如果=y,则xy=6,x和y的乘积一定,那么x和y成反比例;
如果14x=y,则x÷y=,x和y的比值一定,那么x和y成正比例。
故答案为:反;正。
【点评】掌握正、反比例的辨识是解答本题的关键。
12.【分析】根据工作时间一定,工作量和工作效率成正比例,可知甲与乙工作效率的比是:,再化简即可解答。
【解答】解::
=(×12):(×12)
=3:2
答:甲乙工作效率之比是3:2。
故答案为:3:2。
【点评】本题的关键是根据工作时间一定,工作量和工作效率成正比例,求出甲乙两人工作效率的比。
13.【分析】根据圆锥的体积公式:V=πr2h,把数据代入公式求出一个粽子的体积,然后用一个粽子的体积乘每立方厘米糯米的质量,再乘粽子的个数即可。
【解答】解:×3.14×(6÷2)2×5×1.8×100
=×3.14×9×5×1.8×100
=3.14×3×5×1.8×100
=9.42×5×1.8×100
=47.1×1.8×100
=84.78×100
=8478(克)
答:包100个这样的粽子需要糯米8478克。
故答案为:8478。
【点评】此题主要考查圆锥体积公式的灵活运用,关键是熟记公式。
14.【分析】由图可知,从第二个图形开始,每增加一个正方形,就会增加3根小棒;摆2个正方形,需要[4+(2﹣1)×3]根小棒;摆2个正方形,需要[4+(3﹣1)×3]根小棒……;据此规律解答。
【解答】解:4+(5﹣1)×3
=4+12
=16(根)
4+(n﹣1)×3
=4+3n﹣3
=(3n+1)(根)
答:摆第5个需要16根小棒,摆n个需要(3n+1)根小棒。
故答案为:16;(3n+1)。
【点评】解答本题需准确分析搭成的正方形个数与需要的小棒根数之间的关系,灵活找规律解答。
15.【分析】把女生人数看作单位“1”,则男生人数是,合唱团总人数是(1+)。求男生人数比女生少几分之几,用男、女生人数之差除以女生人数;求女生人数是合唱团总人数的百分之几,用女生人数除以合唱团总人数。
【解答】解:(1﹣)÷1
=÷1
=
1÷(1+)
=1÷
=0.625
=62.5%
答:男生人数比女生少,女生人数是合唱团总人数的62.5%。
故答案为:,62.5。
【点评】求一个数比另一个数多或少几分之几,用这两数之差除以另一个数;求一个数是另一个数的百分之几,用这个数除以另一个数。
16.【分析】根据图上距离÷比例尺=实际距离,列式求得甲、乙两地的实际距离,再根据“乙车的速度是甲车的75%,”知道75%的单位“1”是甲车的速度,根据分数乘法的意义求出乙车的速度,再根据路程÷速度和=相遇时间,列式解答即可。
【解答】解:4.2÷=42000000(厘米)
42000000厘米=420千米
420÷(80+80×75%)
=420÷(80+60)
=420÷140
=3(小时)
答:甲地到乙地的实际距离是420千米,经过3小时两车相遇。
故答案为:420,3。
【点评】此题主要考查比例尺、图上距离、实际距离三者之间的数量关系及速度,路程与时间的数量关系。
三.计算题(共4小题)
17.【分析】根据三位数除以一位数、小数加法、分数的加减乘除法、小数加法的计算方法以及0、乘方、百分数的运算计算即可。
【解答】解:
612÷6=102 = 4.67+5.33=10 78×0=0
45×80%=36 0.42=0.16 = =
【点评】熟练掌握三位数除以一位数、小数加法、分数的加减乘除法、小数加法的计算方法以及0、乘方、百分数的运算,是解答本题的关键。
18.【分析】按照减法的性质计算;
把3.2看成0.8×4,再按照乘法交换律和结合律计算;
按照乘法分配律计算;
先算乘法和除法,再算加法;
先算小括号里面的加法,再算除法;
先算小括号里面的加法,再算中括号里面的乘法,最后算除法。
【解答】解:46.7﹣19.13﹣6.87
=46.7﹣(19.13+6.87)
=46.7﹣26
=20.7
1.25×2.5×3.2
=(1.25×0.8)×(4×2.5)
=1×10
=10
=×(+)
=×2
=
35×12+350÷70
=420+5
=425
=22÷
=60
5
=5÷[×]
=5÷
=75
【点评】本题考查了四则混合运算,注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
19.【分析】第一题:在方程两边同时乘即可求出解;
第二题:首先在方程两边同时减去1,然后在方程两边同时除以即可求出解;
第三题:先将方程左边化简,然后在方程两边同时除以(2+30%)的和即可求出解;
第四题:先根据比例的基本性质将比例写成方程的形式,再根据解方程的方法求出解。
【解答】解:
x÷=
x=
x=12﹣1
x=11
x=11÷
x=55
2x+30%x=6.9
2.3x=6.9
x=6.9÷2.3
x=3
x
x=25×4
x=100
x=100÷
x=150
【点评】此题考查解方程和解比例。掌握比例的基性质和等式的性质是解答的关键。
20.【分析】如图,把半圆上的三个点分别命名为点A、点B、点C,由弧AC与弦AC围的阴影部分绕点O顺时针旋转90°后,同由弧BC与弦BC围成的图形重合,阴影部分则合成一个梯形,这个梯形的上底与圆的半径相等,下底是8厘米,高与圆的半径相等,根据“梯形面积=(上底+下底)×高÷2”即可算阴影部分的面积。
【解答】解:(6+8)×6÷2
=14×6÷2
=84÷2
=42(平方厘米)
答:阴影部分的面积为42平方厘米。
【点评】此题重点考查把不规则的阴影部分通过割拼法组合为规则图形再求面积的方法。
四.应用题(共6小题)
21.【分析】用地下总长减去地下总长比地上总长的3倍还多的5.6千米,用求得的差除以3即可求出该市地铁1号线地上总长。
【解答】解:(27.35﹣5.6)÷3
=21.75÷3
=7.25(千米)
答:该市地铁1号线地上总长7.25千米。
【点评】解答此题的关键是理清数量关系,再列式计算。
22.【分析】把女同学收废纸的千克数看作单位“1”,用女同学收废纸的千克数除以对应的分率(1﹣),求出女同学收废纸的千克数,再加男同学收废纸的千克数即可。
【解答】解:20÷(1﹣)+20
=20÷+20
=25+20
=45(千克)
答:六年级同学一共收废纸45千克。
【点评】本题主要考查了分数除法应用题,解题的关键是明确:已知一个数的几分之几是多少,求这个数,用除法计算。
23.【分析】先求出从乙筐取出20%后乙筐梨占甲筐梨的分率,然后将甲筐梨的质量看作单位“1”,用32千克乘所得的分率,求出乙筐梨取出20%后的质量;再除以(1﹣20%),可求出乙筐梨原有的质量,最后与甲筐梨的质量相加即可。
【解答】解:3÷4=
32×÷(1﹣20%)
=24÷80%
=30(千克)
32+30=62(千克)
答:原来甲、乙两筐梨共有62千克。
【点评】本题考查了利用比的知识、分数及百分数乘除混合运算解决问题,需准确分析题目中的数量关系。
24.【分析】根据梯形面积=(上底+下底)×高÷2求出梯形面积,把得数单位平方米换算成公顷,再乘400棵即可解答。
【解答】解:(300+500)×350÷2
=800×350÷2
=280000÷2
=140000(平方米)
140000平方米=14公顷
14×400=5600(棵)
答:这块空地一共可以植树5600棵。
【点评】本题考查的是梯形面积,熟记公式是解答关键。
25.【分析】(1)根据圆柱的侧面积公式:S=πdh,把数据代入公式解答。
(2)通过观察图形可知,纸箱的长等于纸卷底面直径的4倍,宽等于纸卷底面直径的3倍,高等于纸卷的高,根据长方体的容积公式:V=abh,把数据代入公式解答。
【解答】解:(1)3.14×4×10
=12.56×10
=125.6(平方厘米)
答:制作中间的硬纸轴需要125.6平方厘米硬纸板。
(2)4+3.5×2
=4+7
=11(厘米)
(11×4)×(11×3)×10
=44×33×10
=1452×10
=14520(立方厘米)
答:这个长方形纸箱的容积是14520立方厘米。
【点评】此题主要考查圆柱的侧面积公式、长方体的容积公式的灵活运用,关键是熟记公式。
26.【分析】(1)用陈明14岁时的体重减10岁时的体重,再除以10岁时的体重即可。
(2)陈明体重变化的折线纵轴上一格表示2千克,李强体重变化的折线纵轴上一格表示5千克,所以不能根据倾斜度来看体重增长快慢。
【解答】解:(1)(50﹣30)÷30
=20÷30
≈66.7%
答:陈明14岁时的体重比10岁时的体重增加了66.7%。
(2)她说的不正确,陈明体重变化的折线纵轴上一格表示2千克,李强体重变化的折线纵轴上一格表示5千克,所以不能根据倾斜度来看体重增长快慢。
故答案为:66.7。
【点评】本题是复式折线统计图,要通过坐标轴以及图例等读懂本图,根据图中所示的数量解决问题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
