小升初分班考常考题(试题)2023-2024学年数学六年级下册人教版(含答案)
文档属性
| 名称 | 小升初分班考常考题(试题)2023-2024学年数学六年级下册人教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 474.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-11 22:03:15 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
绝密★启用前
小升初分班考常考题(试题)2023-2024学年数学六年级下册人教版
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题
1.如果李明以家为出发点,先向东走6m记作m,然后他又走了m。这时李明距离出发点( )m。
A.8 B.6 C.4 D.2
2.小汽车速度的和公交车速度的相等,那么小汽车和公交车的速度比是( )。
A.3∶2 B.2∶3 C.8∶3 D.3∶8
3.哥哥比弟弟多40%的画片,弟弟比哥哥约少( )的画片。
A.40% B.29% C.50% D.45%
4.学校买了红花、黄花、蓝花准备摆在花坛里,其中红花24盆, ,三种花共买了多少盆?要解决这个问题,可以补充的信息是( )。
A.黄花和蓝花的数量比为3∶5 B.三种花的总数是蓝花的6倍
C.红花比黄花多买了10盆 D.黄花、蓝花的总数比红花多50%
5.婷婷做投掷硬币试验,前4次中,3次正面朝上,1次反面朝上。那么,她投掷第5次时,( )。
A.正面朝上的可能性大 B.反面朝上的可能性大
C.两面朝上的可能性一样大 D.无法确定
6.如下图,将长方形ABCD分别沿长和宽所在的直线旋转一周,得到圆柱(1)和圆柱(2)。这两个圆柱相比较,( )。
A.表面积和体积都相等 B.表面积相等,体积不相等
C.表面积不相等,体积相等 D.表面积和体积都不相等
7.要把一块长400米、宽200米的长方形菜地画在一张16开(18.4厘米×26厘米)的纸上,选用的比例尺最合适的是( )。
A.1∶400 B.1∶800 C.1∶2000 D.1∶8000
8.如果M代表一个非零自然数,那么下列算式中,得数最大的是( )。
A. B.M×96% C. D.M÷(1+20%)
二、填空题
9.我国计划2023年建成全球低轨卫星星座一鸿雁星座系统,该系统将为手机网络用户提供无死角、全覆盖的网络服务。截至2020年7月末,我国三家基础电信企业的4G用户数为十二亿九千万人。横线上的数写作( ),用“四舍五入”法精确到“亿”位约是( )亿
10.的分数单位是( ),再添上( )个这样的分数单位,就得到2。
11.山坡上有a只猴子,兔子的数量是猴子的5倍,山坡上猴子和兔子共有( )只。
12.六(2)班男生人数与女生人数的比是5∶4,男生人数是女生人数的( )%,女生人数是男生人数的( )%。
13.( )+( )=24,请在括号里填入质数。
14.一个精密零件长0.8毫米,画在一幅图上是2厘米,这幅图的比例尺是( )。
15.小丽将一张长方形纸的一半涂上黑色,将另一半的涂上红色,红色部分是这张纸的( )。(填分数)
16.把一根48分米长的铁丝焊接成一个正方体框架(接头处忽略不计),它的棱长是( )分米。
17.有60个图形按规律排列:○△□○△□……,那么第35个图形是( )。
18.小圆的半径是3厘米,大圆的半径是4厘米,小圆和大圆周长的比是( ),面积的比是( )。
三、计算题
19.直接写得数。
20.计算下列各题,能简算的要简算。
21.解方程。
四、解答题
22.某工厂去年用电350万千瓦时,今年比去年节电二成五,今年用电多少万千瓦时?
23.妈妈把五万元钱存入银行,存期为2年,年利率为2.50%。到期时可以取回多少钱?
24.周老师带240元钱去买一批笔记本.在甲商店,看到一种标价为8元的笔记本,周老师感到很满意,问营业员怎么卖?营业员说:“买十本送一本”.到了乙商店,看到同样的笔记本,营业员介绍说:“每本8元.十本起,可打九折”.根据以上信息请你算一下,周老师到那家商店购买合算,为什么?
25.小亚做了一个笔筒,她想给笔筒的侧面和底面贴上彩纸,至少需要用多少彩纸?这个笔筒的体积是多少?
26.今年全国各地都在倡导垃圾分类活动,其中上海市被评为执行最好的城市。至10月底,全市可回收垃圾回收量达5600吨/日,比去年10月平均每日增长460%;湿垃圾分出量约达8710吨/日,比去年10月平均每日增长100%;干垃圾处置量控制低于13000吨/日,比去年10月平均每日减少50%。
(1)去年10月平均每日上海市可回收垃圾回收量达多少吨/日?
(2)去年10月平均每日上海市干垃圾处置量达多少吨/日?
(3)对照今年上海市湿垃圾和干垃圾的增减情况,请你做一个合理的解释。
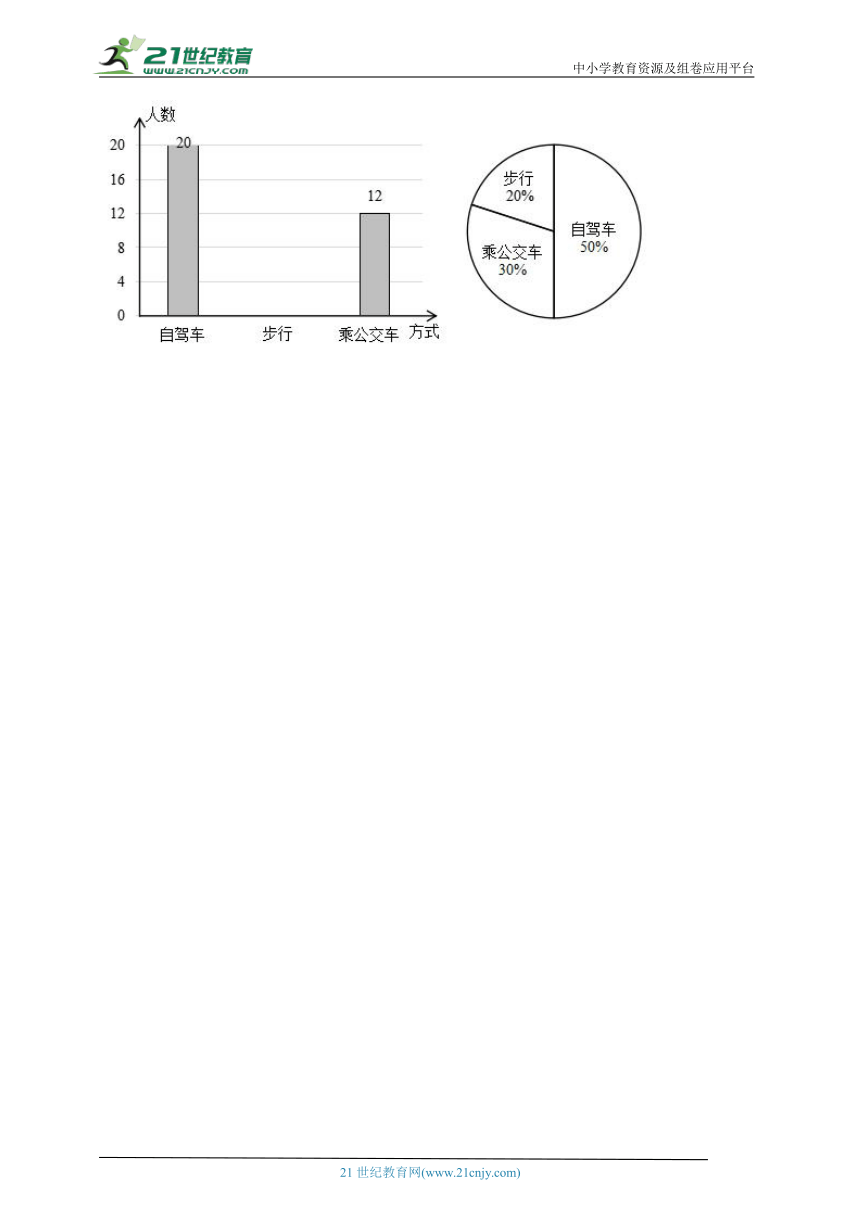
27.学校组织老师去博物馆参展,前往博物馆,自驾车,乘公交车和步行的人数如条形统计图(部分)和扇形统计图所示。
(1)学校共有( )名老师去参展。
(2)步行前往博物馆的有( )名老师。
(3)把条形统计图补充完整。
参考答案:
1.C
【分析】如果向东走记为正,那么向西走记为负;李明以家为出发点,先向东走6m记作+6m,然后他又走了 2m,说明小明是先向东走6m,再向西走2m,两次距离的差就是现在距离出发点的距离。
【详解】(m)
这时李明距离出发点4m。
故答案为:C
【点睛】本题考查正负数,解答本题的关键是掌握正负数表示具有相反意义的量。
2.A
【分析】小汽车速度的和公交车速度的相等,将这句话用数学语言表达出来就是:小汽车速度×=公交车速度×,我们可以假设这两个式子都是等于1,那么汽车速度就是2,公交车速度就是,可以得出小汽车和公交车的速度比=2:,再化简比可得出结果。
【详解】1÷=2
1÷=
小汽车和公交车的速度比是:
2∶
=6∶4
=3∶2
小汽车和公交车的速度比是3∶2。
故答案为:A
3.B
【分析】40%改写成分数就是,此题就变成了“哥哥比弟弟多的画片”,将弟弟的画片数量看作单位“1”。我们可以假设弟弟的画片有5份,则哥哥的画片就有5+5×=7份;题目中要求“弟弟比哥哥约少百分之多少的画片”就相当于是求“5份比7份约少百分之多少的画片”,把哥哥的画片数量看作单位“1”,就可以列式为:(7-5)÷7,再计算即可得出结果。
【详解】40%=
5+5×
=5+2
=7(份)
(7-5)÷7
=2÷7
=
≈0.29=29%
弟弟比哥哥约少29%的画片。
故答案为:B
【点睛】本题主要是考查学生对于单位“1”的理解。
4.D
【分析】要求学校这三种花共买了多少盆,就需要知道黄花、蓝花的总盆数与红花的盆数之间的关系,或者蓝花、黄花分别与红花盆数之间的关系,据此先选择需要补充的信息即可。
【详解】A.黄花和蓝花的数量比为3∶5,与红花盆数无关,所以无法求出黄花、蓝花的盆数;
B.三种花的总数是蓝花的6倍,与红花盆数无关,所以无法求出黄花、蓝花、红花的总盆数;
C.红花比黄花多买了10盆,只能求出黄花盆数,无法求出蓝花盆数,也就无法求出黄花、蓝花、红花的总盆数;
D.黄花、蓝花的总数比红花多50%,把红花的数量看作单位“1”,黄花、蓝花的总数是红花的(1+50%),根据百分数乘法的意义,用24×(1+50%)即可求出黄花、蓝花的总数,再加上红花的数量即可求出三种花的总数;
故答案为:D
【点睛】本题考查百分数,解答本题的关键是根据问题和已知条件补充条件解决问题,需准确分析条件和问题之间的关系。
5.C
【分析】硬币有正反两个面,无论投掷几次,每次投掷,正面和反面朝上的可能性都一样大,据此分析。
【详解】根据分析,她投掷第5次时,两面朝上的可能性一样大。
故答案为:C
6.D
【分析】根据题意,以长方形ABCD分别沿长和宽所在的直线旋转一周,可以得到两种不同的圆柱体。
圆柱(1)是以长方形的长所在的直线为轴,旋转一周,那么形成圆柱的高等于长方形的长,圆柱的底面半径等于长方形的宽;
圆柱(2)是以长方形的宽所在的直线为轴,旋转一周,那么形成圆柱的高等于长方形的宽,圆柱的底面半径等于长方形的长;
然后根据圆柱的表面积公式S表=S侧+2S底,其中S侧=2πrh,S底=πr2,代入数据计算,求出两种圆柱的表面积,再比较大小即可;
根据圆柱的体积公式V=πr2h,代入数据计算,求出两种圆柱的体积,再比较大小,得出结论。
【详解】圆柱(1)的表面积:
2×3.14×3×6+3.14×32×2
=18.84×6+3.14×9×2
=113.04+56.52
=169.56(cm2)
圆柱(1)的体积:
3.14×32×6
=3.14×9×6
=169.56(cm3)
圆柱(2)的表面积:
2×3.14×6×3+3.14×62×2
=37.68×3+3.14×36×2
=113.04+226.08
=339.12(cm2)
圆柱(2)的体积:
3.14×62×3
=3.14×36×3
=339.12(cm3)
表面积:169.56≠339.12
体积:169.56≠339.12
所以,圆柱(1)和圆柱(2)的表面积和体积都不相等。
故答案为:D
7.C
【分析】根据图上距离=实际距离×比例尺,分别计算出各选项比例尺的图上距离,结合纸的大小,选择即可。
【详解】400米=40000厘米、200米=20000厘米
A.40000×=100(厘米)
20000×=50(厘米)
100>26、50>18.4
图上长和宽均大于纸的长和宽,不合适;
B.40000×=50(厘米)
20000×=25(厘米)
50>26、25>18.4
图上长和宽均大于纸的长和宽,不合适;
C.40000×=20(厘米)
20000×=10(厘米)
20<26、10<18.4
图上长和宽均小于纸的长和宽,且大小也合适,合适;
D.40000×=5(厘米)
20000×=2.5(厘米)
5<26、2.5<18.4
虽然图上长和宽均小于纸的长和宽,但是画到纸上的图太小,不合适。
选用的比例尺最合适的是1∶2000。
故答案为:C
8.C
【分析】可以假设M是一个具体的数,比如1,从而求出各个算式的结果,再比较出得数最大的即可。
分数乘法:分子乘分子,分母乘分母,能约分的可先约分,再计算;
百分数的运算:可将百分数写成小数,再计算;
分数除法:除以一个数,就是乘它的倒数。
【详解】令M=1,
A.1×(1+)
=1×
=
=1.2;
B.1×96%=96%=0.96;
C.1÷(1-)
=1÷
=1×
=
=1.333……;
D.1÷(1+20%)
=1÷1.2
=0.8333……
1.333……>1.2>0.96>0.8333……,所以得数最大的是。
故答案为:C
9. 1290000000 13
【分析】根据整数的写法,从高级到低位,一级一级地写,哪一个数位上一个单位也没有,就在那个数位上写0,据此写出此数;精确到“亿”位,就看千万位上的数,再根据“四舍五入”法进行求出近似的,再在数的后面写上“亿”字。
【详解】十二亿九千万写作:1290000000
1290000000≈13亿
【点睛】本题考查整数的写法和求近似数,关键求近似数时要带计数单位。
10. 9
【分析】分母是几分数单位就是几分之一;将2化成分母是7的假分数,求出两个分子的差,就是需要再添上的分数单位的个数,据此分析。
【详解】2=、14-5=9(个)
的分数单位是,再添上9个这样的分数单位,就得到2。
【点睛】分数单位:把单位“1”平均分成若干份,表示其中一份的叫分数单位。
11.6a
【分析】兔子的数量=猴子的数量×5,猴子和兔子的总数量=猴子的数量+兔子的数量,据此解答。
【详解】a+5a=6a(只)
所以,山坡上猴子和兔子共有6a只。
【点睛】掌握含有字母的式子化简的方法是解答题目的关键。
12. 125 80
【分析】男生人数与女生人数的比是5∶4,可以将男生人数看作5,女生人数看作4,男生人数÷女生人数=男生人数是女生人数的百分之几;女生人数÷男生人数=女生人数是男生人数的百分之几。
【详解】5÷4=125%
4÷5=80%
【点睛】关键是理解比的意义,求一个数占另一个数的百分之几用除法。
13. 7 17
【分析】一个大于1的自然数,除了1和它自身外,不能整除其他自然数的数, 即除了1和它本身以外不再有其他因数,这样的数叫质数。
【详解】5+19=24或7+17=24或11+13=24。
【点睛】关键是理解质数、合数的分类标准,找到符合条件的质数。
14.25∶1
【分析】根据图上距离∶实际距离=比例尺,进行分析。
【详解】2厘米∶0.8毫米=20毫米∶0.8毫米=200∶8=25∶1
【点睛】比例尺没有单位名称。为了方便,通常把比例尺的前项化作1(图上距离大于实际距离的,常把后项化为1)。
15.
【分析】把整张长方形的纸看作单位“1”,涂上黑色的部分占整张纸的,剩下部分占整张纸的(1-),红色部分占剩下部分的,用乘法求出红色部分占整张纸的分率,据此解答。
【详解】(1-)×
=×
=
所以,红色部分是这张纸的。
【点睛】已知一个数,求这个数的几分之几是多少用乘法计算。
16.4
【分析】根据正方体棱长=棱长总和÷12,列式计算即可。
【详解】48÷12=4(分米)
【点睛】关键是熟悉正方体特征,正方体有12条棱,所有的棱长度相等。
17.△
【分析】○△□,3个图形一个周期,确定周期后,用总量除以周期,如果正好是整数个周期,结果为周期的最后一个;如果比整数个周期多n个,也就是余数是n,那么结果为下一个周期里的第n个。
【详解】35÷3=11(组)……2(个)
第35个图形是△。
【点睛】解答周期问题的关键是找出周期。
18. 3∶4 9∶16
【分析】根据半径比=周长比,平方以后的比是面积比,进行分析。
【详解】32∶42=9∶16,小圆和大圆周长的比是3∶4,面积的比是9∶16。
【点睛】两数相除又叫两个数的比,圆的周长=2πr,圆的面积=πr2。
19.100;;;0.4;
0.6;10;;3000
【详解】略
20.65.5;;;
;;
【分析】(1)先计算小数除法,再计算乘法,最后计算加法;
(2)交换25%和的位置,利用乘法交换律和乘法结合律简便计算;
(3)先通分计算括号里的减法,再计算括号外的除法;
(4)利用乘法分配律,括号里的两个数分别乘20,再求出它们的和,最后计算除法;
(5)2022拆解成(2021+1),再利用乘法分配律简便计算;
(6)先通分计算小括号里的减法,再计算中括号里的乘法,最后计算中括号外的除法。
【详解】
=37.5+7×4
=37.5+28
=65.5
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
21.;
【分析】(1)根据等式的性质1和性质2,方程左右两边先同时加0.25,再同时除以0.5,解出方程;
(2)根据比例的基本性质,两内项之积等于两外项之积,把比例转化成方程后,再根据等式的性质2,方程左右两边同时除以,解出方程。
【详解】
解:
解:
22.262.5万千瓦时
【分析】由题意可知,把去年用电看做单位“1”,二成五即25%,今年用电是去年用电总量的1-25%,据此列式解答即可。
【详解】350×(1-25%)
=350×75%
=262.5(万千瓦时)
答:今年用电262.5万千瓦时。
【点睛】找准单位“1”,理解成数与百分数的关系是解题关键,求一个数的百分之几是多少用乘法计算即可。
23.52500元
【分析】根据利息=本金×利率×时间,代入数据,求出利息,再加上本金,即可解答。
【详解】五万=50000元
50000×2.50%×2+50000
=1250×2+50000
=2500+50000
=52500(元)
答:到期时可以取回52500元。
【点睛】本题考查利率问题,关键是熟记利息公式。
24.乙点购买合算
【详解】根据“甲店买十送一本”,可得到:240÷8=30本,有3个10,还要赠送3本,再加点花240元买了33本笔记本,乙店十本起打九折,因为周老师买的本数肯定在10本以上,所以就是打九折,可以计算一下乙店买33本所花的钱:33×8×90%=237.6元,通过比较发现237.3<240,所以到乙店购买合算.
25.376.8平方厘米;653.12立方厘米
【分析】根据题意,求至少需要用多少彩纸,就是求这个圆柱形笔筒的表面积去掉一个底面的面积,根据圆柱的表面积公式:侧面积+底面积,代入数据,求出需要的彩纸的面积;再根据圆柱的体积公式:底面积×高,代入数据,即可解答。
【详解】3.14×(8÷2)2+3.14×8×13
=3.14×16+25.12×13
=50.24+326.56
=376.8(平方厘米)
3.14×(8÷2)2×13
=3.14×16×13
=50.24×13
=653.12(立方厘米)
答:至少需要用376.8平方厘米的彩纸,这个笔筒的体积是653.12立方厘米。
【点睛】利用圆柱的表面积公式、体积公式进行解答,关键是熟记公式。
26.(1)1000吨/日;
(2)26000吨/日;
(3)上海市垃圾分类做得越来越好,干垃圾处置量减少很多,环境变得更好。
【分析】(1)全市可回收量为5600吨/日,比去年10月平均每日增长460%,用5600除以1+460%,即可得解;
(2)干垃圾处置量控制低于13000吨/日,比去年10月平均每日减少50%,用13000除以1-50%,即可得解;
(3)从数据来看,上海市的可回收垃圾增加明显,干垃圾处置量减少明显,垃圾分类做的越来越好,环境也更好。
【详解】(1)5600÷(1+460%)
=5600×
=1000(吨/日)
答:去年10月平均每日上海市可回收垃圾回收量达1000吨/日。
(2)13000÷(1-50%)
=13000×2
=26000(吨/日)
答:去年10月平均每日上海市干垃圾处置量达26000吨/日。
(3)答:上海市垃圾分类做得越来越好,干垃圾处置量减少很多,环境变得更好。
【点睛】本题主要考查百分比的计算。
27.(1)40;(2)8;(3)见详解
【分析】(1)把总人数看作单位“1”,其中自驾去参展的有20人,占总人数的50%,根据已知一个数的百分之几是多少,求这个数,用除法解答;(2)步行前往的占20%,根据求一个数的百分之几是多少,用乘法解答;(3)根据步行的人数,完成条形统计图。
【详解】(1)20÷50%=40(名)
(2)40×20%=8(名)
(3)条形统计图补充如下:
【点睛】本题主要考查的是理解掌握扇形统计图、条形统计图的特点及作用,解答本题的关键是根据统计图提供的信息,解决有关的实际问题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
绝密★启用前
小升初分班考常考题(试题)2023-2024学年数学六年级下册人教版
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题
1.如果李明以家为出发点,先向东走6m记作m,然后他又走了m。这时李明距离出发点( )m。
A.8 B.6 C.4 D.2
2.小汽车速度的和公交车速度的相等,那么小汽车和公交车的速度比是( )。
A.3∶2 B.2∶3 C.8∶3 D.3∶8
3.哥哥比弟弟多40%的画片,弟弟比哥哥约少( )的画片。
A.40% B.29% C.50% D.45%
4.学校买了红花、黄花、蓝花准备摆在花坛里,其中红花24盆, ,三种花共买了多少盆?要解决这个问题,可以补充的信息是( )。
A.黄花和蓝花的数量比为3∶5 B.三种花的总数是蓝花的6倍
C.红花比黄花多买了10盆 D.黄花、蓝花的总数比红花多50%
5.婷婷做投掷硬币试验,前4次中,3次正面朝上,1次反面朝上。那么,她投掷第5次时,( )。
A.正面朝上的可能性大 B.反面朝上的可能性大
C.两面朝上的可能性一样大 D.无法确定
6.如下图,将长方形ABCD分别沿长和宽所在的直线旋转一周,得到圆柱(1)和圆柱(2)。这两个圆柱相比较,( )。
A.表面积和体积都相等 B.表面积相等,体积不相等
C.表面积不相等,体积相等 D.表面积和体积都不相等
7.要把一块长400米、宽200米的长方形菜地画在一张16开(18.4厘米×26厘米)的纸上,选用的比例尺最合适的是( )。
A.1∶400 B.1∶800 C.1∶2000 D.1∶8000
8.如果M代表一个非零自然数,那么下列算式中,得数最大的是( )。
A. B.M×96% C. D.M÷(1+20%)
二、填空题
9.我国计划2023年建成全球低轨卫星星座一鸿雁星座系统,该系统将为手机网络用户提供无死角、全覆盖的网络服务。截至2020年7月末,我国三家基础电信企业的4G用户数为十二亿九千万人。横线上的数写作( ),用“四舍五入”法精确到“亿”位约是( )亿
10.的分数单位是( ),再添上( )个这样的分数单位,就得到2。
11.山坡上有a只猴子,兔子的数量是猴子的5倍,山坡上猴子和兔子共有( )只。
12.六(2)班男生人数与女生人数的比是5∶4,男生人数是女生人数的( )%,女生人数是男生人数的( )%。
13.( )+( )=24,请在括号里填入质数。
14.一个精密零件长0.8毫米,画在一幅图上是2厘米,这幅图的比例尺是( )。
15.小丽将一张长方形纸的一半涂上黑色,将另一半的涂上红色,红色部分是这张纸的( )。(填分数)
16.把一根48分米长的铁丝焊接成一个正方体框架(接头处忽略不计),它的棱长是( )分米。
17.有60个图形按规律排列:○△□○△□……,那么第35个图形是( )。
18.小圆的半径是3厘米,大圆的半径是4厘米,小圆和大圆周长的比是( ),面积的比是( )。
三、计算题
19.直接写得数。
20.计算下列各题,能简算的要简算。
21.解方程。
四、解答题
22.某工厂去年用电350万千瓦时,今年比去年节电二成五,今年用电多少万千瓦时?
23.妈妈把五万元钱存入银行,存期为2年,年利率为2.50%。到期时可以取回多少钱?
24.周老师带240元钱去买一批笔记本.在甲商店,看到一种标价为8元的笔记本,周老师感到很满意,问营业员怎么卖?营业员说:“买十本送一本”.到了乙商店,看到同样的笔记本,营业员介绍说:“每本8元.十本起,可打九折”.根据以上信息请你算一下,周老师到那家商店购买合算,为什么?
25.小亚做了一个笔筒,她想给笔筒的侧面和底面贴上彩纸,至少需要用多少彩纸?这个笔筒的体积是多少?
26.今年全国各地都在倡导垃圾分类活动,其中上海市被评为执行最好的城市。至10月底,全市可回收垃圾回收量达5600吨/日,比去年10月平均每日增长460%;湿垃圾分出量约达8710吨/日,比去年10月平均每日增长100%;干垃圾处置量控制低于13000吨/日,比去年10月平均每日减少50%。
(1)去年10月平均每日上海市可回收垃圾回收量达多少吨/日?
(2)去年10月平均每日上海市干垃圾处置量达多少吨/日?
(3)对照今年上海市湿垃圾和干垃圾的增减情况,请你做一个合理的解释。
27.学校组织老师去博物馆参展,前往博物馆,自驾车,乘公交车和步行的人数如条形统计图(部分)和扇形统计图所示。
(1)学校共有( )名老师去参展。
(2)步行前往博物馆的有( )名老师。
(3)把条形统计图补充完整。
参考答案:
1.C
【分析】如果向东走记为正,那么向西走记为负;李明以家为出发点,先向东走6m记作+6m,然后他又走了 2m,说明小明是先向东走6m,再向西走2m,两次距离的差就是现在距离出发点的距离。
【详解】(m)
这时李明距离出发点4m。
故答案为:C
【点睛】本题考查正负数,解答本题的关键是掌握正负数表示具有相反意义的量。
2.A
【分析】小汽车速度的和公交车速度的相等,将这句话用数学语言表达出来就是:小汽车速度×=公交车速度×,我们可以假设这两个式子都是等于1,那么汽车速度就是2,公交车速度就是,可以得出小汽车和公交车的速度比=2:,再化简比可得出结果。
【详解】1÷=2
1÷=
小汽车和公交车的速度比是:
2∶
=6∶4
=3∶2
小汽车和公交车的速度比是3∶2。
故答案为:A
3.B
【分析】40%改写成分数就是,此题就变成了“哥哥比弟弟多的画片”,将弟弟的画片数量看作单位“1”。我们可以假设弟弟的画片有5份,则哥哥的画片就有5+5×=7份;题目中要求“弟弟比哥哥约少百分之多少的画片”就相当于是求“5份比7份约少百分之多少的画片”,把哥哥的画片数量看作单位“1”,就可以列式为:(7-5)÷7,再计算即可得出结果。
【详解】40%=
5+5×
=5+2
=7(份)
(7-5)÷7
=2÷7
=
≈0.29=29%
弟弟比哥哥约少29%的画片。
故答案为:B
【点睛】本题主要是考查学生对于单位“1”的理解。
4.D
【分析】要求学校这三种花共买了多少盆,就需要知道黄花、蓝花的总盆数与红花的盆数之间的关系,或者蓝花、黄花分别与红花盆数之间的关系,据此先选择需要补充的信息即可。
【详解】A.黄花和蓝花的数量比为3∶5,与红花盆数无关,所以无法求出黄花、蓝花的盆数;
B.三种花的总数是蓝花的6倍,与红花盆数无关,所以无法求出黄花、蓝花、红花的总盆数;
C.红花比黄花多买了10盆,只能求出黄花盆数,无法求出蓝花盆数,也就无法求出黄花、蓝花、红花的总盆数;
D.黄花、蓝花的总数比红花多50%,把红花的数量看作单位“1”,黄花、蓝花的总数是红花的(1+50%),根据百分数乘法的意义,用24×(1+50%)即可求出黄花、蓝花的总数,再加上红花的数量即可求出三种花的总数;
故答案为:D
【点睛】本题考查百分数,解答本题的关键是根据问题和已知条件补充条件解决问题,需准确分析条件和问题之间的关系。
5.C
【分析】硬币有正反两个面,无论投掷几次,每次投掷,正面和反面朝上的可能性都一样大,据此分析。
【详解】根据分析,她投掷第5次时,两面朝上的可能性一样大。
故答案为:C
6.D
【分析】根据题意,以长方形ABCD分别沿长和宽所在的直线旋转一周,可以得到两种不同的圆柱体。
圆柱(1)是以长方形的长所在的直线为轴,旋转一周,那么形成圆柱的高等于长方形的长,圆柱的底面半径等于长方形的宽;
圆柱(2)是以长方形的宽所在的直线为轴,旋转一周,那么形成圆柱的高等于长方形的宽,圆柱的底面半径等于长方形的长;
然后根据圆柱的表面积公式S表=S侧+2S底,其中S侧=2πrh,S底=πr2,代入数据计算,求出两种圆柱的表面积,再比较大小即可;
根据圆柱的体积公式V=πr2h,代入数据计算,求出两种圆柱的体积,再比较大小,得出结论。
【详解】圆柱(1)的表面积:
2×3.14×3×6+3.14×32×2
=18.84×6+3.14×9×2
=113.04+56.52
=169.56(cm2)
圆柱(1)的体积:
3.14×32×6
=3.14×9×6
=169.56(cm3)
圆柱(2)的表面积:
2×3.14×6×3+3.14×62×2
=37.68×3+3.14×36×2
=113.04+226.08
=339.12(cm2)
圆柱(2)的体积:
3.14×62×3
=3.14×36×3
=339.12(cm3)
表面积:169.56≠339.12
体积:169.56≠339.12
所以,圆柱(1)和圆柱(2)的表面积和体积都不相等。
故答案为:D
7.C
【分析】根据图上距离=实际距离×比例尺,分别计算出各选项比例尺的图上距离,结合纸的大小,选择即可。
【详解】400米=40000厘米、200米=20000厘米
A.40000×=100(厘米)
20000×=50(厘米)
100>26、50>18.4
图上长和宽均大于纸的长和宽,不合适;
B.40000×=50(厘米)
20000×=25(厘米)
50>26、25>18.4
图上长和宽均大于纸的长和宽,不合适;
C.40000×=20(厘米)
20000×=10(厘米)
20<26、10<18.4
图上长和宽均小于纸的长和宽,且大小也合适,合适;
D.40000×=5(厘米)
20000×=2.5(厘米)
5<26、2.5<18.4
虽然图上长和宽均小于纸的长和宽,但是画到纸上的图太小,不合适。
选用的比例尺最合适的是1∶2000。
故答案为:C
8.C
【分析】可以假设M是一个具体的数,比如1,从而求出各个算式的结果,再比较出得数最大的即可。
分数乘法:分子乘分子,分母乘分母,能约分的可先约分,再计算;
百分数的运算:可将百分数写成小数,再计算;
分数除法:除以一个数,就是乘它的倒数。
【详解】令M=1,
A.1×(1+)
=1×
=
=1.2;
B.1×96%=96%=0.96;
C.1÷(1-)
=1÷
=1×
=
=1.333……;
D.1÷(1+20%)
=1÷1.2
=0.8333……
1.333……>1.2>0.96>0.8333……,所以得数最大的是。
故答案为:C
9. 1290000000 13
【分析】根据整数的写法,从高级到低位,一级一级地写,哪一个数位上一个单位也没有,就在那个数位上写0,据此写出此数;精确到“亿”位,就看千万位上的数,再根据“四舍五入”法进行求出近似的,再在数的后面写上“亿”字。
【详解】十二亿九千万写作:1290000000
1290000000≈13亿
【点睛】本题考查整数的写法和求近似数,关键求近似数时要带计数单位。
10. 9
【分析】分母是几分数单位就是几分之一;将2化成分母是7的假分数,求出两个分子的差,就是需要再添上的分数单位的个数,据此分析。
【详解】2=、14-5=9(个)
的分数单位是,再添上9个这样的分数单位,就得到2。
【点睛】分数单位:把单位“1”平均分成若干份,表示其中一份的叫分数单位。
11.6a
【分析】兔子的数量=猴子的数量×5,猴子和兔子的总数量=猴子的数量+兔子的数量,据此解答。
【详解】a+5a=6a(只)
所以,山坡上猴子和兔子共有6a只。
【点睛】掌握含有字母的式子化简的方法是解答题目的关键。
12. 125 80
【分析】男生人数与女生人数的比是5∶4,可以将男生人数看作5,女生人数看作4,男生人数÷女生人数=男生人数是女生人数的百分之几;女生人数÷男生人数=女生人数是男生人数的百分之几。
【详解】5÷4=125%
4÷5=80%
【点睛】关键是理解比的意义,求一个数占另一个数的百分之几用除法。
13. 7 17
【分析】一个大于1的自然数,除了1和它自身外,不能整除其他自然数的数, 即除了1和它本身以外不再有其他因数,这样的数叫质数。
【详解】5+19=24或7+17=24或11+13=24。
【点睛】关键是理解质数、合数的分类标准,找到符合条件的质数。
14.25∶1
【分析】根据图上距离∶实际距离=比例尺,进行分析。
【详解】2厘米∶0.8毫米=20毫米∶0.8毫米=200∶8=25∶1
【点睛】比例尺没有单位名称。为了方便,通常把比例尺的前项化作1(图上距离大于实际距离的,常把后项化为1)。
15.
【分析】把整张长方形的纸看作单位“1”,涂上黑色的部分占整张纸的,剩下部分占整张纸的(1-),红色部分占剩下部分的,用乘法求出红色部分占整张纸的分率,据此解答。
【详解】(1-)×
=×
=
所以,红色部分是这张纸的。
【点睛】已知一个数,求这个数的几分之几是多少用乘法计算。
16.4
【分析】根据正方体棱长=棱长总和÷12,列式计算即可。
【详解】48÷12=4(分米)
【点睛】关键是熟悉正方体特征,正方体有12条棱,所有的棱长度相等。
17.△
【分析】○△□,3个图形一个周期,确定周期后,用总量除以周期,如果正好是整数个周期,结果为周期的最后一个;如果比整数个周期多n个,也就是余数是n,那么结果为下一个周期里的第n个。
【详解】35÷3=11(组)……2(个)
第35个图形是△。
【点睛】解答周期问题的关键是找出周期。
18. 3∶4 9∶16
【分析】根据半径比=周长比,平方以后的比是面积比,进行分析。
【详解】32∶42=9∶16,小圆和大圆周长的比是3∶4,面积的比是9∶16。
【点睛】两数相除又叫两个数的比,圆的周长=2πr,圆的面积=πr2。
19.100;;;0.4;
0.6;10;;3000
【详解】略
20.65.5;;;
;;
【分析】(1)先计算小数除法,再计算乘法,最后计算加法;
(2)交换25%和的位置,利用乘法交换律和乘法结合律简便计算;
(3)先通分计算括号里的减法,再计算括号外的除法;
(4)利用乘法分配律,括号里的两个数分别乘20,再求出它们的和,最后计算除法;
(5)2022拆解成(2021+1),再利用乘法分配律简便计算;
(6)先通分计算小括号里的减法,再计算中括号里的乘法,最后计算中括号外的除法。
【详解】
=37.5+7×4
=37.5+28
=65.5
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
21.;
【分析】(1)根据等式的性质1和性质2,方程左右两边先同时加0.25,再同时除以0.5,解出方程;
(2)根据比例的基本性质,两内项之积等于两外项之积,把比例转化成方程后,再根据等式的性质2,方程左右两边同时除以,解出方程。
【详解】
解:
解:
22.262.5万千瓦时
【分析】由题意可知,把去年用电看做单位“1”,二成五即25%,今年用电是去年用电总量的1-25%,据此列式解答即可。
【详解】350×(1-25%)
=350×75%
=262.5(万千瓦时)
答:今年用电262.5万千瓦时。
【点睛】找准单位“1”,理解成数与百分数的关系是解题关键,求一个数的百分之几是多少用乘法计算即可。
23.52500元
【分析】根据利息=本金×利率×时间,代入数据,求出利息,再加上本金,即可解答。
【详解】五万=50000元
50000×2.50%×2+50000
=1250×2+50000
=2500+50000
=52500(元)
答:到期时可以取回52500元。
【点睛】本题考查利率问题,关键是熟记利息公式。
24.乙点购买合算
【详解】根据“甲店买十送一本”,可得到:240÷8=30本,有3个10,还要赠送3本,再加点花240元买了33本笔记本,乙店十本起打九折,因为周老师买的本数肯定在10本以上,所以就是打九折,可以计算一下乙店买33本所花的钱:33×8×90%=237.6元,通过比较发现237.3<240,所以到乙店购买合算.
25.376.8平方厘米;653.12立方厘米
【分析】根据题意,求至少需要用多少彩纸,就是求这个圆柱形笔筒的表面积去掉一个底面的面积,根据圆柱的表面积公式:侧面积+底面积,代入数据,求出需要的彩纸的面积;再根据圆柱的体积公式:底面积×高,代入数据,即可解答。
【详解】3.14×(8÷2)2+3.14×8×13
=3.14×16+25.12×13
=50.24+326.56
=376.8(平方厘米)
3.14×(8÷2)2×13
=3.14×16×13
=50.24×13
=653.12(立方厘米)
答:至少需要用376.8平方厘米的彩纸,这个笔筒的体积是653.12立方厘米。
【点睛】利用圆柱的表面积公式、体积公式进行解答,关键是熟记公式。
26.(1)1000吨/日;
(2)26000吨/日;
(3)上海市垃圾分类做得越来越好,干垃圾处置量减少很多,环境变得更好。
【分析】(1)全市可回收量为5600吨/日,比去年10月平均每日增长460%,用5600除以1+460%,即可得解;
(2)干垃圾处置量控制低于13000吨/日,比去年10月平均每日减少50%,用13000除以1-50%,即可得解;
(3)从数据来看,上海市的可回收垃圾增加明显,干垃圾处置量减少明显,垃圾分类做的越来越好,环境也更好。
【详解】(1)5600÷(1+460%)
=5600×
=1000(吨/日)
答:去年10月平均每日上海市可回收垃圾回收量达1000吨/日。
(2)13000÷(1-50%)
=13000×2
=26000(吨/日)
答:去年10月平均每日上海市干垃圾处置量达26000吨/日。
(3)答:上海市垃圾分类做得越来越好,干垃圾处置量减少很多,环境变得更好。
【点睛】本题主要考查百分比的计算。
27.(1)40;(2)8;(3)见详解
【分析】(1)把总人数看作单位“1”,其中自驾去参展的有20人,占总人数的50%,根据已知一个数的百分之几是多少,求这个数,用除法解答;(2)步行前往的占20%,根据求一个数的百分之几是多少,用乘法解答;(3)根据步行的人数,完成条形统计图。
【详解】(1)20÷50%=40(名)
(2)40×20%=8(名)
(3)条形统计图补充如下:
【点睛】本题主要考查的是理解掌握扇形统计图、条形统计图的特点及作用,解答本题的关键是根据统计图提供的信息,解决有关的实际问题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
