第十一章 三角形预习检测卷(含解析)
文档属性
| 名称 | 第十一章 三角形预习检测卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 758.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-12 18:34:54 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第十一章三角形预习检测卷-数学八年级下册人教版
一、选择题
1.如图,在人字梯的中间有一“拉杆”,这样做的数学原理是( )
A.三角形具有稳定性 B.垂线段最短
C.两直线平行,内错角相等 D.两点之间,线段最短
2.若一个多边形的每个内角都为,则它的边数为( )
A.4 B.5 C.6 D.7
3.如果三角形的一个外角小于与它相邻的内角,那么这个三角形是( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.等腰直角三角形
4.将一副三角板按如图所示的方式摆放,,与交于点,则的度数为( )
A. B. C. D.
5.下列说法正确的是( )
A.若,则为锐角三角形
B.若,则为锐角三角形
C.若,则为锐角三角形
D.若且,则为锐角三角形
6.如图,是的中线,点E是的中点,连接,若,则四边形的面积为( )
A.10 B.12 C.15 D.18
7.如图,已知a//b,∠1=120°,∠2=90°,则∠3的度数是( )
A.120° B.130° C.140° D.150°
8.直线l与正六边形ABCDEF的边AB,EF分别相交于点M,N,如图所示,则α+β=( )
A.115° B.120° C.135° D.144°
9.如图,△ABC的面积为1cm2,AP垂直∠B的平分线BP于P,则△PBC的面积为( )
A.0.4 cm2 B.0.5 cm2 C.0.6 cm2 D.0.7 cm2
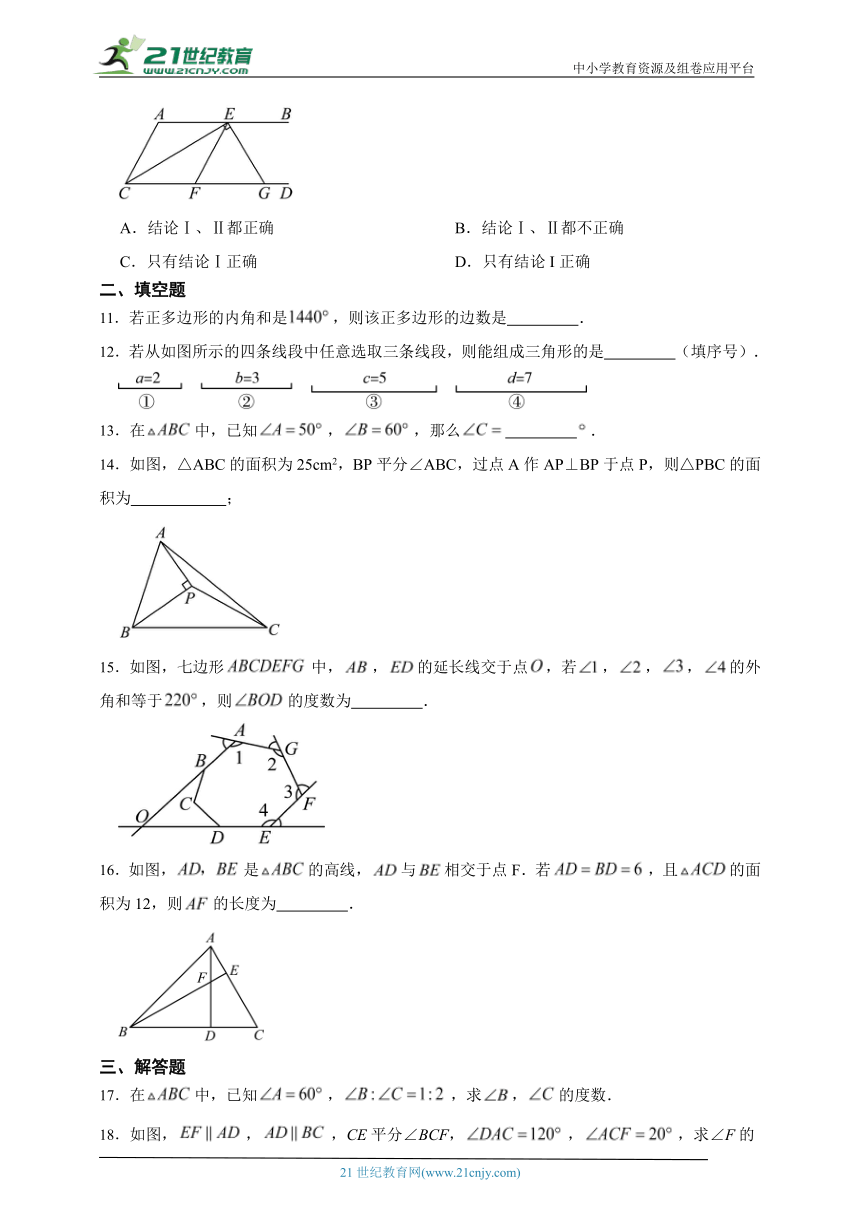
10.如图,,,,垂足为,平分.关于结论Ⅰ、Ⅱ,下列判断正确的是
结论Ⅰ:
结论Ⅱ:若的度数每增加,则的度数会减少
A.结论Ⅰ、Ⅱ都正确 B.结论Ⅰ、Ⅱ都不正确
C.只有结论Ⅰ正确 D.只有结论I正确
二、填空题
11.若正多边形的内角和是,则该正多边形的边数是 .
12.若从如图所示的四条线段中任意选取三条线段,则能组成三角形的是 (填序号).
13.在中,已知,,那么 .
14.如图,△ABC的面积为25cm2,BP平分∠ABC,过点A作AP⊥BP于点P,则△PBC的面积为 ;
15.如图,七边形中,,的延长线交于点,若,,,的外角和等于,则的度数为 .
16.如图,是的高线,与相交于点F.若,且的面积为12,则的长度为 .
三、解答题
17.在中,已知,,求,的度数.
18.如图,,,CE平分∠BCF,,,求∠F的度数.
19.已知的三边长均为整数,的周长为奇数.
(1)若,,求AB的长.
(2)若,求AB的最小值.
20.阅读明明和芳芳的对话,解答下列问题.
(1)明明通过计算,发现少加了一个锐角,则这个“少加的锐角”的度数是_________°.
(2)在(1)的条件下,明明求的是几边形的内角和?
(3)在(1)的条件下,若这是一个正多边形,则这个正多边形的每一个外角的度数是多少?
21.如图,已知平分,是的高,若,,求的度数.
22. 如图,已知∠1+∠2=180°,且∠AFE=∠ACB.
(1)求证:∠3=∠B;
(2)若CE平分∠ACB,且∠2=110°,∠3=50°,求∠ACB的度数.
23.秦九韶(1208年~1268年),字道古,南宋著名数学家.与李冶、杨辉、朱世杰并称宋元数学四大家,他精研星象、音律、算术、诗词、弓剑、营造之学,他于1247年完成著作《数学九章》中关于三角形的面积公式与古希腊几何学家海伦的成果并称“海伦 秦九韶公式”,它的主要内容是,如果一个三角形的三边长分别是a,b,c,记,S为三角形的面积,那么.
(1)如图在中,,,,请用上面的公式计算的面积;
(2)一个三角形的三边长分别为a,b,c,,,求的值,
24.在平面直角坐标系中,O为坐标原点,过点分别作x轴、y轴的垂线,交x轴于点C,交y轴于点B,动点P从点C出发,沿以每秒3个单位长度的速度向终点B运动,运动时间为t(秒),a,b满足.
(1)直接写出点B和点C的坐标;
(2)用含t的式子表示线段的长,并写出t的取值范围;
(3)已知点,连接,,在(2)条件下是否存在t值,使四边形的面积是三角形的面积的3倍,若存在,请求出t值及点P的坐标,若不存在,请说明理由.
答案解析部分
1.【答案】A
2.【答案】B
3.【答案】B
4.【答案】A
5.【答案】C
6.【答案】C
7.【答案】D
8.【答案】B
9.【答案】B
10.【答案】A
11.【答案】10
12.【答案】②③④
13.【答案】
14.【答案】
15.【答案】
16.【答案】2
17.【答案】,
18.【答案】解:∵CE平分∠ACF,∴
∴∴∴
又∴
∴
∴
19.【答案】(1)7或9;(2)6.
20.【答案】(1)
(2)
(3)
21.【答案】
22.【答案】(1)证明:∵∠1+∠2=180°,∠1+∠FDE=180°,
∴∠FDE=∠2,
∴,
∴∠3=∠AEF,
∵∠AFE=∠ACB,
∴,
∴∠AEF=∠B,
∴∠B=∠3;
(2)解:∵∠3=∠B,∠3=50°,
∴∠B=50°,
∵∠2+∠B+∠ECB=180°,∠2=110°,
∴∠ECB=20°,
∵CE平分∠ACB,
∴∠ACB=2∠ECB=40°.
23.【答案】(1)解:由题意,,
∴.
即的面积为;
(2)解:由题意,,
∴,
∵,
∴
∴.
∴,即
∴.
24.【答案】(1),;
(2)当时,,当时,;
(3)存在;,点P的坐标为;,点P的坐标为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第十一章三角形预习检测卷-数学八年级下册人教版
一、选择题
1.如图,在人字梯的中间有一“拉杆”,这样做的数学原理是( )
A.三角形具有稳定性 B.垂线段最短
C.两直线平行,内错角相等 D.两点之间,线段最短
2.若一个多边形的每个内角都为,则它的边数为( )
A.4 B.5 C.6 D.7
3.如果三角形的一个外角小于与它相邻的内角,那么这个三角形是( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.等腰直角三角形
4.将一副三角板按如图所示的方式摆放,,与交于点,则的度数为( )
A. B. C. D.
5.下列说法正确的是( )
A.若,则为锐角三角形
B.若,则为锐角三角形
C.若,则为锐角三角形
D.若且,则为锐角三角形
6.如图,是的中线,点E是的中点,连接,若,则四边形的面积为( )
A.10 B.12 C.15 D.18
7.如图,已知a//b,∠1=120°,∠2=90°,则∠3的度数是( )
A.120° B.130° C.140° D.150°
8.直线l与正六边形ABCDEF的边AB,EF分别相交于点M,N,如图所示,则α+β=( )
A.115° B.120° C.135° D.144°
9.如图,△ABC的面积为1cm2,AP垂直∠B的平分线BP于P,则△PBC的面积为( )
A.0.4 cm2 B.0.5 cm2 C.0.6 cm2 D.0.7 cm2
10.如图,,,,垂足为,平分.关于结论Ⅰ、Ⅱ,下列判断正确的是
结论Ⅰ:
结论Ⅱ:若的度数每增加,则的度数会减少
A.结论Ⅰ、Ⅱ都正确 B.结论Ⅰ、Ⅱ都不正确
C.只有结论Ⅰ正确 D.只有结论I正确
二、填空题
11.若正多边形的内角和是,则该正多边形的边数是 .
12.若从如图所示的四条线段中任意选取三条线段,则能组成三角形的是 (填序号).
13.在中,已知,,那么 .
14.如图,△ABC的面积为25cm2,BP平分∠ABC,过点A作AP⊥BP于点P,则△PBC的面积为 ;
15.如图,七边形中,,的延长线交于点,若,,,的外角和等于,则的度数为 .
16.如图,是的高线,与相交于点F.若,且的面积为12,则的长度为 .
三、解答题
17.在中,已知,,求,的度数.
18.如图,,,CE平分∠BCF,,,求∠F的度数.
19.已知的三边长均为整数,的周长为奇数.
(1)若,,求AB的长.
(2)若,求AB的最小值.
20.阅读明明和芳芳的对话,解答下列问题.
(1)明明通过计算,发现少加了一个锐角,则这个“少加的锐角”的度数是_________°.
(2)在(1)的条件下,明明求的是几边形的内角和?
(3)在(1)的条件下,若这是一个正多边形,则这个正多边形的每一个外角的度数是多少?
21.如图,已知平分,是的高,若,,求的度数.
22. 如图,已知∠1+∠2=180°,且∠AFE=∠ACB.
(1)求证:∠3=∠B;
(2)若CE平分∠ACB,且∠2=110°,∠3=50°,求∠ACB的度数.
23.秦九韶(1208年~1268年),字道古,南宋著名数学家.与李冶、杨辉、朱世杰并称宋元数学四大家,他精研星象、音律、算术、诗词、弓剑、营造之学,他于1247年完成著作《数学九章》中关于三角形的面积公式与古希腊几何学家海伦的成果并称“海伦 秦九韶公式”,它的主要内容是,如果一个三角形的三边长分别是a,b,c,记,S为三角形的面积,那么.
(1)如图在中,,,,请用上面的公式计算的面积;
(2)一个三角形的三边长分别为a,b,c,,,求的值,
24.在平面直角坐标系中,O为坐标原点,过点分别作x轴、y轴的垂线,交x轴于点C,交y轴于点B,动点P从点C出发,沿以每秒3个单位长度的速度向终点B运动,运动时间为t(秒),a,b满足.
(1)直接写出点B和点C的坐标;
(2)用含t的式子表示线段的长,并写出t的取值范围;
(3)已知点,连接,,在(2)条件下是否存在t值,使四边形的面积是三角形的面积的3倍,若存在,请求出t值及点P的坐标,若不存在,请说明理由.
答案解析部分
1.【答案】A
2.【答案】B
3.【答案】B
4.【答案】A
5.【答案】C
6.【答案】C
7.【答案】D
8.【答案】B
9.【答案】B
10.【答案】A
11.【答案】10
12.【答案】②③④
13.【答案】
14.【答案】
15.【答案】
16.【答案】2
17.【答案】,
18.【答案】解:∵CE平分∠ACF,∴
∴∴∴
又∴
∴
∴
19.【答案】(1)7或9;(2)6.
20.【答案】(1)
(2)
(3)
21.【答案】
22.【答案】(1)证明:∵∠1+∠2=180°,∠1+∠FDE=180°,
∴∠FDE=∠2,
∴,
∴∠3=∠AEF,
∵∠AFE=∠ACB,
∴,
∴∠AEF=∠B,
∴∠B=∠3;
(2)解:∵∠3=∠B,∠3=50°,
∴∠B=50°,
∵∠2+∠B+∠ECB=180°,∠2=110°,
∴∠ECB=20°,
∵CE平分∠ACB,
∴∠ACB=2∠ECB=40°.
23.【答案】(1)解:由题意,,
∴.
即的面积为;
(2)解:由题意,,
∴,
∵,
∴
∴.
∴,即
∴.
24.【答案】(1),;
(2)当时,,当时,;
(3)存在;,点P的坐标为;,点P的坐标为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
