六年级下册数学北师大版图形与几何(课件)(共24张PPT)
文档属性
| 名称 | 六年级下册数学北师大版图形与几何(课件)(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-11 00:00:00 | ||
图片预览




文档简介
(共24张PPT)
北师大六年级下册数学总复习
图形与几何(七)
h
r
0
h
r
0
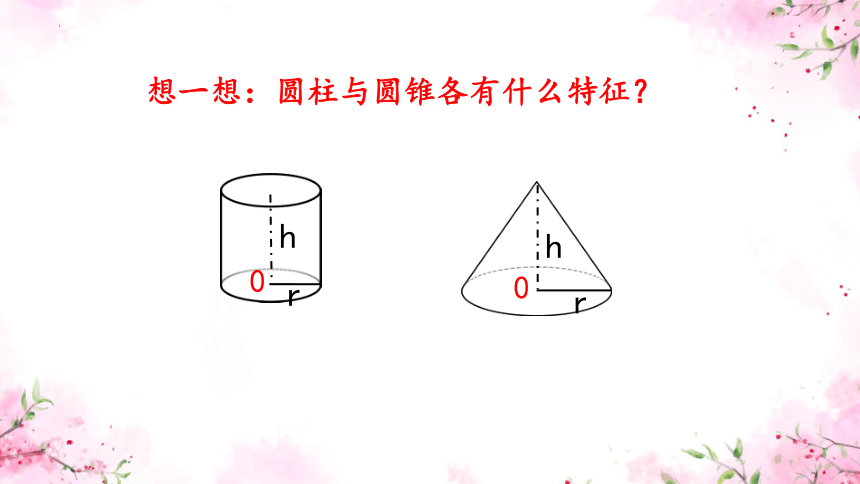
想一想:圆柱与圆锥各有什么特征?
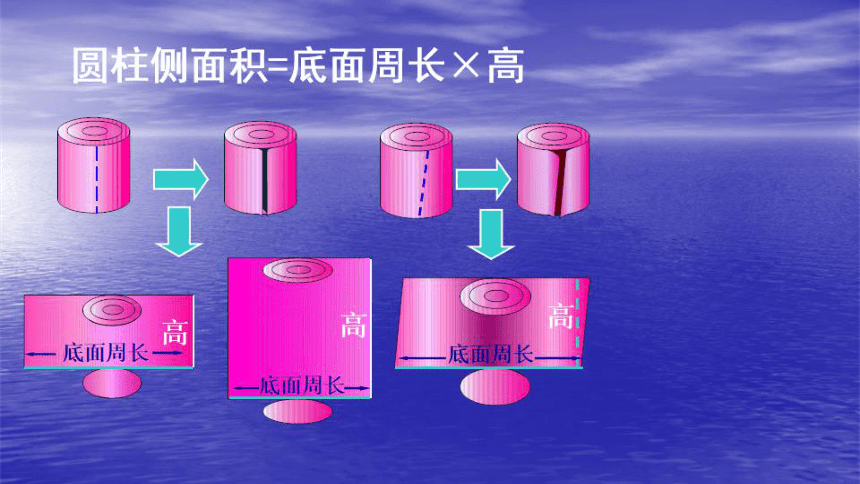
S圆柱=2πrh + 2
2πr
h
πr
πr
πr
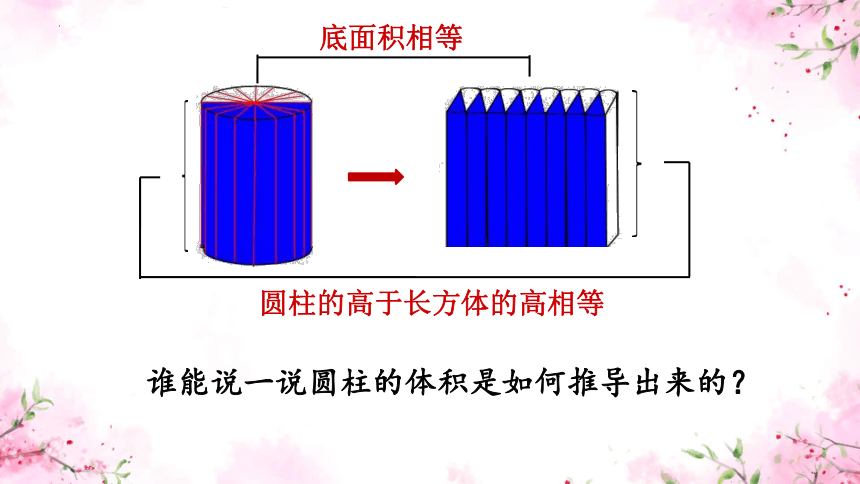
底面积相等
圆柱的高于长方体的高相等
谁能说一说圆柱的体积是如何推导出来的?
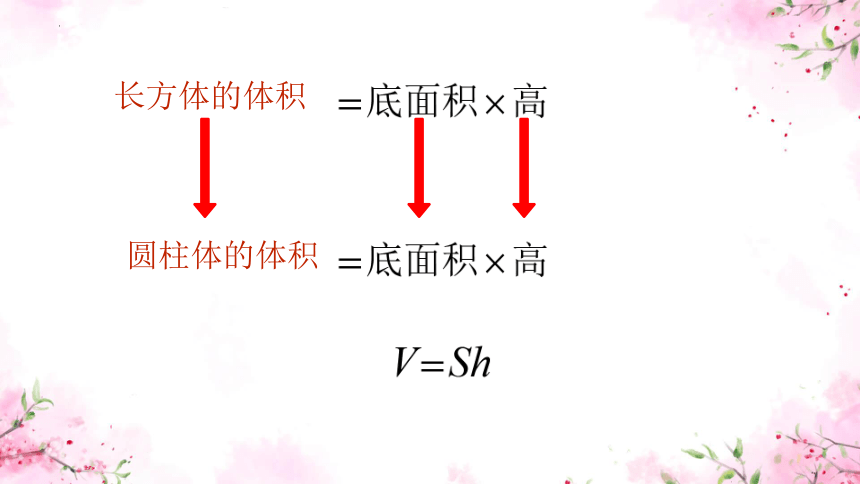
长方体的体积
圆柱体的体积
字母表示v= sh
圆锥体积=底面积×高×
圆锥的体积等于与它等底等高圆柱体积的 。
⑴ 一个圆柱的体积是 300 立方厘米,高与它等底等高的圆锥的体积是( )立方厘米。
⑵ 一个圆锥的体积 是 90 立方厘米,与是它等底等高的圆柱的体积是( )立立方厘米。
⑶ 一个圆柱的体积是 60 立方分米,比与它等底等高的圆锥的体积多( )立方分米。
100
270
40
基础练习
⑷ 把一个圆柱切削成一个最大的圆锥,已知削去部分的体积比圆锥体积多3.6立方分米,那么圆锥的体积是 ( )立方分米。
⑸ 一个圆锥和一个圆柱等底等高,它们的体积之和是 120 立方分米,这个圆柱的体积是( )立方分米;圆锥体积比圆柱少( )立方分米。
3.6
90
60
基础练习
(6)等底等高的圆柱和圆锥,如果先在圆锥容器中注满水,水面高12厘米,再全部倒入圆柱形容器中,水面高( )厘米;如果先在圆柱容器中注满水,再把水倒入圆锥形容器直到注满,这时圆柱形容器中的水面高( )厘米。
(7)在等低等高的情况下,圆柱的体积与圆锥体积的比是( );圆柱的体积比圆锥的体积多( )%,圆锥的体积比圆柱的体积少( )
4
8
3:1
200%
基础练习
基础练习
⑴ 一个圆柱与一个圆锥的体积和底面积都相等,圆柱的高是 9 分米,圆锥的高是 ( )分米。
⑵ 一个圆锥与一个圆柱等底等体,圆锥的的高是 24 厘米,圆柱的高比圆锥矮( ) 厘米。
⑶ 如果圆柱与圆锥等积等底,它们高的相差 12 厘米,则圆柱的高是 ( )厘米;它们高的和是 ( )厘米。
27
16
6
24
基础练习
把一团圆柱体橡皮泥揉成与它等底的圆锥体,高将 ( )。
A、扩大到原来的3倍
B、缩小到原来的
C、扩大到原来的6倍
D、缩小到原来的
A
基础练习
圆柱体的底面半径和高都扩大3倍, 它的体积扩大的倍数是( )。
A.3 B.6 C.9 D.27
D
基础练习
高相等、底面周长也相等,体积最大的是( )。
A.长方体 B.圆锥体 C.圆柱体
C
基础练习
一个圆柱的体积是等底的圆锥体积的6倍,这个圆柱的高是圆锥高的( )
A 6倍 B 3倍 C 2倍
C
基础练习
压路机的前轮是圆柱形,轮宽1.5米,直径1.2米,前轮每分钟转动10周,每分钟前进多少米?每分钟压路多少平方米?
基础练习
答:每分钟前进37.68米;每分钟压路56.52平方米。
一个圆锥形沙堆的底面周长是12.56米,高是6米,这个沙堆的体积是多少立方米?
基础练习
答:这个沙堆的体积是25.12立方米。
把一个底面半径是3厘米,高是10厘米的圆锥形容器灌满水,然后把水倒入一个底面半径是5厘米的圆柱形容器里,求圆柱形容器内水面的高度?
基础练习
答:圆柱形容器内水面的高度是1.2厘米。
把一个圆柱的底面半径是2厘米,高2米的木头,削成一个最大的方木,这个方木的体积是多少?
拓展练习
答:这个方木的体积是1600立方厘米。
如图,想想办法,你能否求它的体积 ( 单位:厘米)
2
6
4
拓展练习
通过本节课的复
习你有什么收获?
北师大六年级下册数学总复习
图形与几何(七)
h
r
0
h
r
0
想一想:圆柱与圆锥各有什么特征?
S圆柱=2πrh + 2
2πr
h
πr
πr
πr
底面积相等
圆柱的高于长方体的高相等
谁能说一说圆柱的体积是如何推导出来的?
长方体的体积
圆柱体的体积
字母表示v= sh
圆锥体积=底面积×高×
圆锥的体积等于与它等底等高圆柱体积的 。
⑴ 一个圆柱的体积是 300 立方厘米,高与它等底等高的圆锥的体积是( )立方厘米。
⑵ 一个圆锥的体积 是 90 立方厘米,与是它等底等高的圆柱的体积是( )立立方厘米。
⑶ 一个圆柱的体积是 60 立方分米,比与它等底等高的圆锥的体积多( )立方分米。
100
270
40
基础练习
⑷ 把一个圆柱切削成一个最大的圆锥,已知削去部分的体积比圆锥体积多3.6立方分米,那么圆锥的体积是 ( )立方分米。
⑸ 一个圆锥和一个圆柱等底等高,它们的体积之和是 120 立方分米,这个圆柱的体积是( )立方分米;圆锥体积比圆柱少( )立方分米。
3.6
90
60
基础练习
(6)等底等高的圆柱和圆锥,如果先在圆锥容器中注满水,水面高12厘米,再全部倒入圆柱形容器中,水面高( )厘米;如果先在圆柱容器中注满水,再把水倒入圆锥形容器直到注满,这时圆柱形容器中的水面高( )厘米。
(7)在等低等高的情况下,圆柱的体积与圆锥体积的比是( );圆柱的体积比圆锥的体积多( )%,圆锥的体积比圆柱的体积少( )
4
8
3:1
200%
基础练习
基础练习
⑴ 一个圆柱与一个圆锥的体积和底面积都相等,圆柱的高是 9 分米,圆锥的高是 ( )分米。
⑵ 一个圆锥与一个圆柱等底等体,圆锥的的高是 24 厘米,圆柱的高比圆锥矮( ) 厘米。
⑶ 如果圆柱与圆锥等积等底,它们高的相差 12 厘米,则圆柱的高是 ( )厘米;它们高的和是 ( )厘米。
27
16
6
24
基础练习
把一团圆柱体橡皮泥揉成与它等底的圆锥体,高将 ( )。
A、扩大到原来的3倍
B、缩小到原来的
C、扩大到原来的6倍
D、缩小到原来的
A
基础练习
圆柱体的底面半径和高都扩大3倍, 它的体积扩大的倍数是( )。
A.3 B.6 C.9 D.27
D
基础练习
高相等、底面周长也相等,体积最大的是( )。
A.长方体 B.圆锥体 C.圆柱体
C
基础练习
一个圆柱的体积是等底的圆锥体积的6倍,这个圆柱的高是圆锥高的( )
A 6倍 B 3倍 C 2倍
C
基础练习
压路机的前轮是圆柱形,轮宽1.5米,直径1.2米,前轮每分钟转动10周,每分钟前进多少米?每分钟压路多少平方米?
基础练习
答:每分钟前进37.68米;每分钟压路56.52平方米。
一个圆锥形沙堆的底面周长是12.56米,高是6米,这个沙堆的体积是多少立方米?
基础练习
答:这个沙堆的体积是25.12立方米。
把一个底面半径是3厘米,高是10厘米的圆锥形容器灌满水,然后把水倒入一个底面半径是5厘米的圆柱形容器里,求圆柱形容器内水面的高度?
基础练习
答:圆柱形容器内水面的高度是1.2厘米。
把一个圆柱的底面半径是2厘米,高2米的木头,削成一个最大的方木,这个方木的体积是多少?
拓展练习
答:这个方木的体积是1600立方厘米。
如图,想想办法,你能否求它的体积 ( 单位:厘米)
2
6
4
拓展练习
通过本节课的复
习你有什么收获?
