【湘教版数学八年级上册同步练习】 第二章三角形综合题(含答案)
文档属性
| 名称 | 【湘教版数学八年级上册同步练习】 第二章三角形综合题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-11 17:10:38 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【湘教版数学八年级上册同步练习】
第二章三角形综合题
一、单选题
1.已知三角形的两边分别为4和10,则此三角形的第三边可能是( )
A.4 B.5 C.9 D.14
2.下列说法错误的是( )
A.对角线相等的菱形是正方形
B.矩形的对角线相等
C.两组对边分别相等的四边形是平行四边形
D.对角线互相垂直的平行四边形是矩形
3.下列命题是假命题的是( )
A.对顶角相等 B.同角的补角相等
C.内错角相等 D.直角都相等
4.已知直线,将以,为两腰的等腰的顶点P,N按如图所示的方式分别放在a,b上,若,,则( )
A. B. C. D.
5.能判定 与 全等的条件是( )
A. , , B. , ,
C. , , D. , ,
二、填空题
6. 如图,∠ABC=∠DCB,请补充一个条件: ,使△ABC≌△DCB.
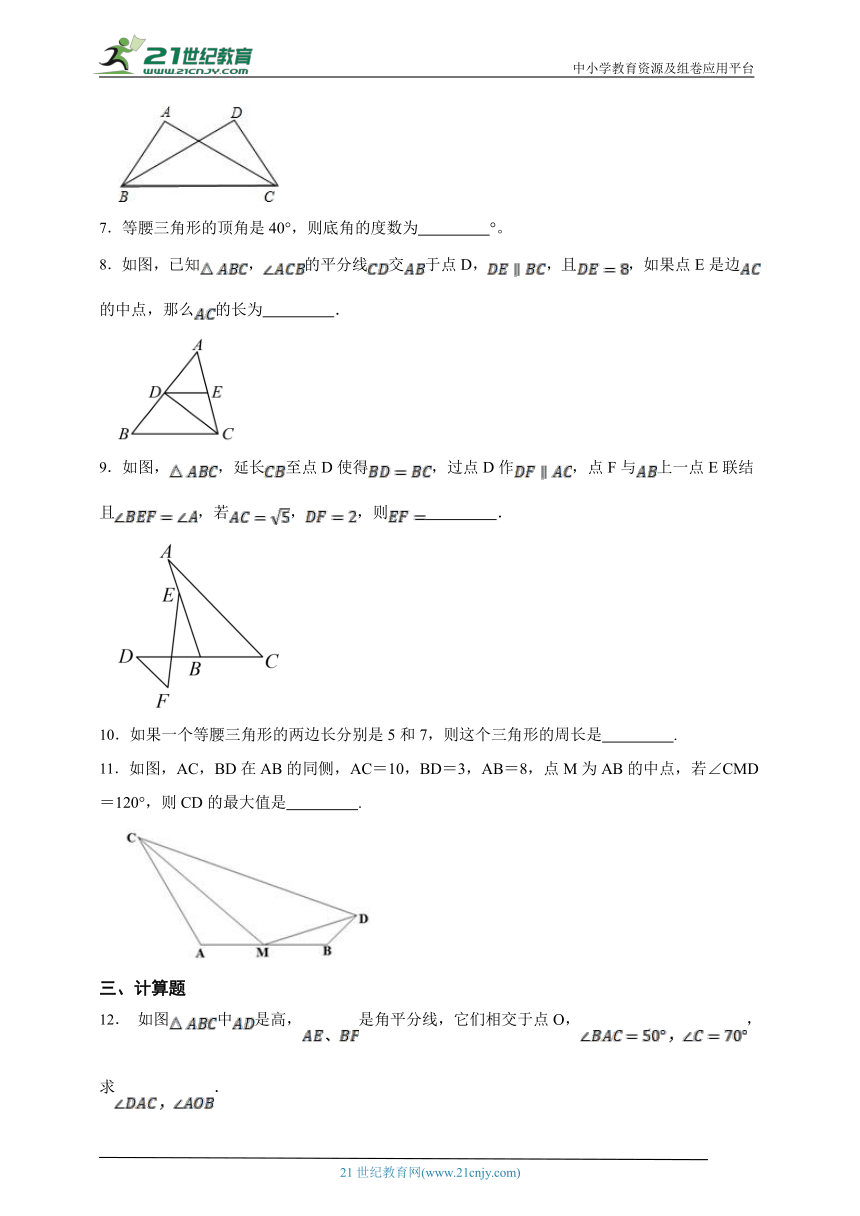
7.等腰三角形的顶角是40°,则底角的度数为 °。
8.如图,已知,的平分线交于点D,,且,如果点E是边的中点,那么的长为 .
9.如图,,延长至点D使得,过点D作,点F与上一点E联结且,若,,则 .
10.如果一个等腰三角形的两边长分别是5和7,则这个三角形的周长是 .
11.如图,AC,BD在AB的同侧,AC=10,BD=3,AB=8,点M为AB的中点,若∠CMD=120°,则CD的最大值是 .
三、计算题
12. 如图中是高,是角平分线,它们相交于点O,,求.
13.已知△ABC的三个内角分别是∠A、∠B、∠C,若∠A=30°,∠C=2∠B,求∠B的度数.
四、解答题
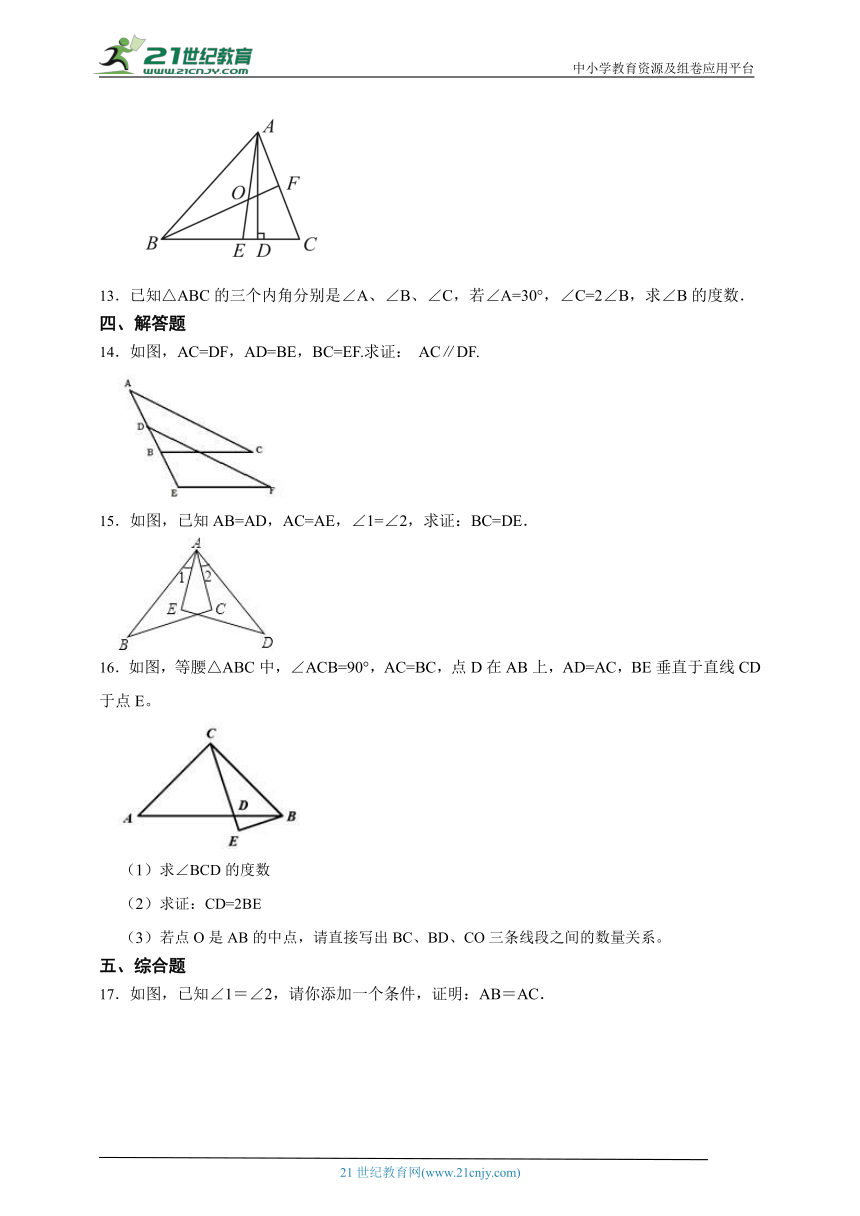
14.如图,AC=DF,AD=BE,BC=EF.求证: AC∥DF.
15.如图,已知AB=AD,AC=AE,∠1=∠2,求证:BC=DE.
16.如图,等腰△ABC中,∠ACB=90°,AC=BC,点D在AB上,AD=AC,BE垂直于直线CD于点E。
(1)求∠BCD的度数
(2)求证:CD=2BE
(3)若点O是AB的中点,请直接写出BC、BD、CO三条线段之间的数量关系。
五、综合题
17.如图,已知∠1=∠2,请你添加一个条件,证明:AB=AC.
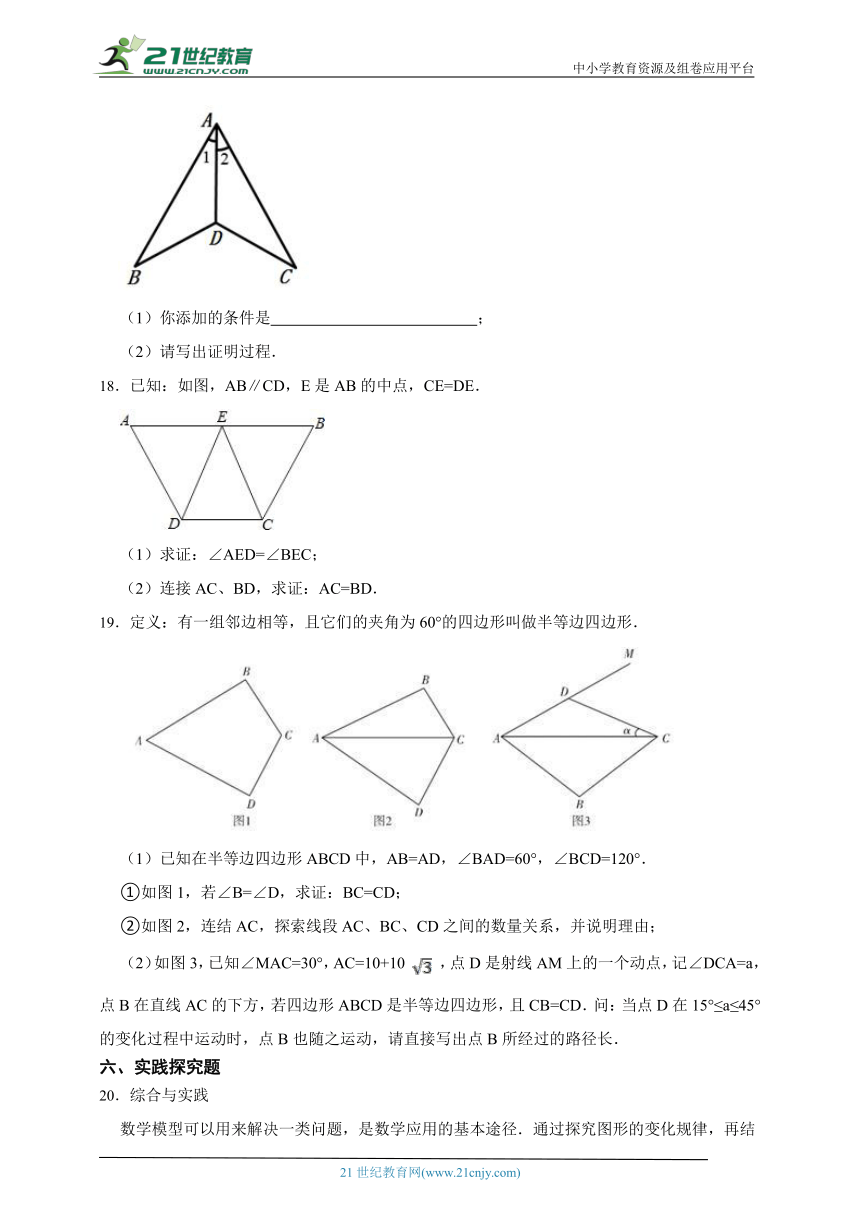
(1)你添加的条件是 ;
(2)请写出证明过程.
18.已知:如图,AB∥CD,E是AB的中点,CE=DE.
(1)求证:∠AED=∠BEC;
(2)连接AC、BD,求证:AC=BD.
19.定义:有一组邻边相等,且它们的夹角为60°的四边形叫做半等边四边形.
(1)已知在半等边四边形ABCD中,AB=AD,∠BAD=60°,∠BCD=120°.
①如图1,若∠B=∠D,求证:BC=CD;
②如图2,连结AC,探索线段AC、BC、CD之间的数量关系,并说明理由;
(2)如图3,已知∠MAC=30°,AC=10+10 ,点D是射线AM上的一个动点,记∠DCA=a,点B在直线AC的下方,若四边形ABCD是半等边四边形,且CB=CD.问:当点D在15°≤a≤45°的变化过程中运动时,点B也随之运动,请直接写出点B所经过的路径长.
六、实践探究题
20.综合与实践
数学模型可以用来解决一类问题,是数学应用的基本途径.通过探究图形的变化规律,再结合其他数学知识的内在联系,最终可以获得宝贵的数学经验,并将其运用到更广阔的数学天地.
(1)发现问题:如图1,在和中,,,,连接,,延长交于点.则与的数量关系: , ;
(2)类比探究:如图2,在和中,,,,连接,,延长,交于点.请猜想与的数量关系及的度数,并说明理由.
答案解析部分
1.【答案】C
【知识点】三角形三边关系
2.【答案】D
【知识点】真命题与假命题
3.【答案】C
【知识点】余角、补角及其性质;平行线的性质;对顶角及其性质;真命题与假命题
4.【答案】C
【知识点】平行线的性质;等腰三角形的性质
5.【答案】D
【知识点】三角形全等的判定
6.【答案】AB=DC(或者∠A=∠D)
【知识点】三角形全等的判定
7.【答案】70
【知识点】三角形内角和定理;等腰三角形的性质
8.【答案】16
【知识点】等腰三角形的判定;内错角的概念
9.【答案】
【知识点】平行线的性质;等腰三角形的性质;三角形全等的判定-ASA
10.【答案】17或19
【知识点】三角形三边关系;等腰三角形的性质
11.【答案】22
【知识点】等边三角形的判定与性质;轴对称的性质
12.【答案】,
【知识点】三角形的角平分线、中线和高;三角形内角和定理
13.【答案】解:∵∠A=30°,
∴∠B+∠C=180°﹣∠A=150°,
∵∠C=2∠B,
∴3∠B=150°,
∴∠B=50°.
【知识点】三角形内角和定理
14.【答案】证明: ∵AD=BE
∴AD+DB=BE+DB,
即AB="DE"
在⊿ABC和⊿DEF中
AB=DE
BC=EF,
AC=DF
∴⊿ABC≌⊿DEF(SSS)
∴∠BAC=∠EDF
∴AC//DF.
【知识点】平行线的判定;全等三角形的判定与性质
15.【答案】证明:∵∠1=∠2,
∴∠1+∠EAC=∠2+∠EAC,即∠BAC=∠DAE,
在△ABC和△ADE中
,
∴△ABC≌△ADE,
∴BC=DE
【知识点】全等三角形的判定与性质
16.【答案】(1)解:由CB=AC,∠BCA=90°,得∠A=∠CBA=45°,
在△ACD中,AC=AD,
∴∠ACD=67.5°
∴∠BCD=90°-∠ACD=22.5°
(2)解:过点A作AF⊥CD于F,AC=AD,
∴CD=2CF,
又∵BE⊥直线CD于E,
∴∠BEC=∠AFC=90°
又∵∠BCE+∠DCA=∠FAC+∠DCA=90°
∴∠BCE=∠CAF
又∵BC=AC,
∴ △CBE≌△ACF
∴ CF=BE.
即CD=2CF=2BE.
(3)解:BC=2CO-BD
【知识点】全等三角形的判定与性质
17.【答案】(1)∠B=∠C(答案不唯一)
(2)解:∵∠1=∠2,∠B=∠C,AD=AD,
∴△ABD≌△ACD,
∴AB=AC.
【知识点】三角形全等的判定-ASA
18.【答案】(1)证明:∵CE=DE,∴∠EDC=∠ECD,又∵AB∥CD,
∴∠AED=∠EDC,∠BEC=∠ECD
∴∠AED=∠BEC
(2)解:如图,∵∠AED=∠BEC,∴∠AEC=∠BED,∵E是AB的中点,∴AE=BE在△AEC和△BED中, ,
∴△AEC≌△BED.
∴AC=BD
【知识点】平行线的性质;全等三角形的判定与性质;等腰三角形的判定
19.【答案】(1)解:①证明:连结AC,
∵∠A+∠B+∠C+∠D=360°,且∠A=60°,∠C=120°,
∴∠B+∠D=180°,
且∠B=∠D,
∴∠B=∠D=90°,
∵AB=AD,AC=AC,
∴△ABC≌△ADC(HL),
∴BC=DC;
②解:延长CB,使得CD=BE,
∵∠BAD=60°,∠BCD=120°,
∴∠ABC+∠D=180°,
且∠ABC+∠ABE=180°,
∴∠D=∠ABE,
又∵AB=AD
∴△ABE≌△ADC,
∴AE=AC,
∠BAE=∠DAC,
∴∠EAC=∠BAE+∠BAC=∠DAC+∠BAC=∠BAD=60°,
∴△ACE是等边三角形,
∴AC=CE=CB+BE=CB+CD
(2)解:如图,设∠ACD=15°,∠DCD‘=30°,作CM⊥AD,D‘H⊥AC,
由旋转图形的特点可知,
CB=CD,CB‘=CD’,∠BCB'=DCD‘=30°,
∴△∠BCB'≌△DCD‘,
BB'=DD’,
设D'H=x,
由勾股定理得:AH=x, HC=x,
则AC=x+x=10+10 ,
解得x=10, 即D'H=10,
得AH=10,AD’=20,
在Rt△AMC中,
∵AC=10+10,∠DAC=30°,
∴CM=5+5,AM=(5+5),
D'M=AM-AD'=(5+5)-20=5-5,
DM=CM=5+5 ,
∴DD‘=DM-D'M=5+5-5+5=10 .
DD’为D点的运动路程,则BB‘的运动路程也为10 .
【知识点】三角形全等的判定;旋转的性质
20.【答案】(1);
(2)解:,,
理由如下:,
,
即,
在和中,
,
,
,,
,,
,
.
【知识点】三角形内角和定理;三角形全等及其性质;三角形全等的判定-SAS
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【湘教版数学八年级上册同步练习】
第二章三角形综合题
一、单选题
1.已知三角形的两边分别为4和10,则此三角形的第三边可能是( )
A.4 B.5 C.9 D.14
2.下列说法错误的是( )
A.对角线相等的菱形是正方形
B.矩形的对角线相等
C.两组对边分别相等的四边形是平行四边形
D.对角线互相垂直的平行四边形是矩形
3.下列命题是假命题的是( )
A.对顶角相等 B.同角的补角相等
C.内错角相等 D.直角都相等
4.已知直线,将以,为两腰的等腰的顶点P,N按如图所示的方式分别放在a,b上,若,,则( )
A. B. C. D.
5.能判定 与 全等的条件是( )
A. , , B. , ,
C. , , D. , ,
二、填空题
6. 如图,∠ABC=∠DCB,请补充一个条件: ,使△ABC≌△DCB.
7.等腰三角形的顶角是40°,则底角的度数为 °。
8.如图,已知,的平分线交于点D,,且,如果点E是边的中点,那么的长为 .
9.如图,,延长至点D使得,过点D作,点F与上一点E联结且,若,,则 .
10.如果一个等腰三角形的两边长分别是5和7,则这个三角形的周长是 .
11.如图,AC,BD在AB的同侧,AC=10,BD=3,AB=8,点M为AB的中点,若∠CMD=120°,则CD的最大值是 .
三、计算题
12. 如图中是高,是角平分线,它们相交于点O,,求.
13.已知△ABC的三个内角分别是∠A、∠B、∠C,若∠A=30°,∠C=2∠B,求∠B的度数.
四、解答题
14.如图,AC=DF,AD=BE,BC=EF.求证: AC∥DF.
15.如图,已知AB=AD,AC=AE,∠1=∠2,求证:BC=DE.
16.如图,等腰△ABC中,∠ACB=90°,AC=BC,点D在AB上,AD=AC,BE垂直于直线CD于点E。
(1)求∠BCD的度数
(2)求证:CD=2BE
(3)若点O是AB的中点,请直接写出BC、BD、CO三条线段之间的数量关系。
五、综合题
17.如图,已知∠1=∠2,请你添加一个条件,证明:AB=AC.
(1)你添加的条件是 ;
(2)请写出证明过程.
18.已知:如图,AB∥CD,E是AB的中点,CE=DE.
(1)求证:∠AED=∠BEC;
(2)连接AC、BD,求证:AC=BD.
19.定义:有一组邻边相等,且它们的夹角为60°的四边形叫做半等边四边形.
(1)已知在半等边四边形ABCD中,AB=AD,∠BAD=60°,∠BCD=120°.
①如图1,若∠B=∠D,求证:BC=CD;
②如图2,连结AC,探索线段AC、BC、CD之间的数量关系,并说明理由;
(2)如图3,已知∠MAC=30°,AC=10+10 ,点D是射线AM上的一个动点,记∠DCA=a,点B在直线AC的下方,若四边形ABCD是半等边四边形,且CB=CD.问:当点D在15°≤a≤45°的变化过程中运动时,点B也随之运动,请直接写出点B所经过的路径长.
六、实践探究题
20.综合与实践
数学模型可以用来解决一类问题,是数学应用的基本途径.通过探究图形的变化规律,再结合其他数学知识的内在联系,最终可以获得宝贵的数学经验,并将其运用到更广阔的数学天地.
(1)发现问题:如图1,在和中,,,,连接,,延长交于点.则与的数量关系: , ;
(2)类比探究:如图2,在和中,,,,连接,,延长,交于点.请猜想与的数量关系及的度数,并说明理由.
答案解析部分
1.【答案】C
【知识点】三角形三边关系
2.【答案】D
【知识点】真命题与假命题
3.【答案】C
【知识点】余角、补角及其性质;平行线的性质;对顶角及其性质;真命题与假命题
4.【答案】C
【知识点】平行线的性质;等腰三角形的性质
5.【答案】D
【知识点】三角形全等的判定
6.【答案】AB=DC(或者∠A=∠D)
【知识点】三角形全等的判定
7.【答案】70
【知识点】三角形内角和定理;等腰三角形的性质
8.【答案】16
【知识点】等腰三角形的判定;内错角的概念
9.【答案】
【知识点】平行线的性质;等腰三角形的性质;三角形全等的判定-ASA
10.【答案】17或19
【知识点】三角形三边关系;等腰三角形的性质
11.【答案】22
【知识点】等边三角形的判定与性质;轴对称的性质
12.【答案】,
【知识点】三角形的角平分线、中线和高;三角形内角和定理
13.【答案】解:∵∠A=30°,
∴∠B+∠C=180°﹣∠A=150°,
∵∠C=2∠B,
∴3∠B=150°,
∴∠B=50°.
【知识点】三角形内角和定理
14.【答案】证明: ∵AD=BE
∴AD+DB=BE+DB,
即AB="DE"
在⊿ABC和⊿DEF中
AB=DE
BC=EF,
AC=DF
∴⊿ABC≌⊿DEF(SSS)
∴∠BAC=∠EDF
∴AC//DF.
【知识点】平行线的判定;全等三角形的判定与性质
15.【答案】证明:∵∠1=∠2,
∴∠1+∠EAC=∠2+∠EAC,即∠BAC=∠DAE,
在△ABC和△ADE中
,
∴△ABC≌△ADE,
∴BC=DE
【知识点】全等三角形的判定与性质
16.【答案】(1)解:由CB=AC,∠BCA=90°,得∠A=∠CBA=45°,
在△ACD中,AC=AD,
∴∠ACD=67.5°
∴∠BCD=90°-∠ACD=22.5°
(2)解:过点A作AF⊥CD于F,AC=AD,
∴CD=2CF,
又∵BE⊥直线CD于E,
∴∠BEC=∠AFC=90°
又∵∠BCE+∠DCA=∠FAC+∠DCA=90°
∴∠BCE=∠CAF
又∵BC=AC,
∴ △CBE≌△ACF
∴ CF=BE.
即CD=2CF=2BE.
(3)解:BC=2CO-BD
【知识点】全等三角形的判定与性质
17.【答案】(1)∠B=∠C(答案不唯一)
(2)解:∵∠1=∠2,∠B=∠C,AD=AD,
∴△ABD≌△ACD,
∴AB=AC.
【知识点】三角形全等的判定-ASA
18.【答案】(1)证明:∵CE=DE,∴∠EDC=∠ECD,又∵AB∥CD,
∴∠AED=∠EDC,∠BEC=∠ECD
∴∠AED=∠BEC
(2)解:如图,∵∠AED=∠BEC,∴∠AEC=∠BED,∵E是AB的中点,∴AE=BE在△AEC和△BED中, ,
∴△AEC≌△BED.
∴AC=BD
【知识点】平行线的性质;全等三角形的判定与性质;等腰三角形的判定
19.【答案】(1)解:①证明:连结AC,
∵∠A+∠B+∠C+∠D=360°,且∠A=60°,∠C=120°,
∴∠B+∠D=180°,
且∠B=∠D,
∴∠B=∠D=90°,
∵AB=AD,AC=AC,
∴△ABC≌△ADC(HL),
∴BC=DC;
②解:延长CB,使得CD=BE,
∵∠BAD=60°,∠BCD=120°,
∴∠ABC+∠D=180°,
且∠ABC+∠ABE=180°,
∴∠D=∠ABE,
又∵AB=AD
∴△ABE≌△ADC,
∴AE=AC,
∠BAE=∠DAC,
∴∠EAC=∠BAE+∠BAC=∠DAC+∠BAC=∠BAD=60°,
∴△ACE是等边三角形,
∴AC=CE=CB+BE=CB+CD
(2)解:如图,设∠ACD=15°,∠DCD‘=30°,作CM⊥AD,D‘H⊥AC,
由旋转图形的特点可知,
CB=CD,CB‘=CD’,∠BCB'=DCD‘=30°,
∴△∠BCB'≌△DCD‘,
BB'=DD’,
设D'H=x,
由勾股定理得:AH=x, HC=x,
则AC=x+x=10+10 ,
解得x=10, 即D'H=10,
得AH=10,AD’=20,
在Rt△AMC中,
∵AC=10+10,∠DAC=30°,
∴CM=5+5,AM=(5+5),
D'M=AM-AD'=(5+5)-20=5-5,
DM=CM=5+5 ,
∴DD‘=DM-D'M=5+5-5+5=10 .
DD’为D点的运动路程,则BB‘的运动路程也为10 .
【知识点】三角形全等的判定;旋转的性质
20.【答案】(1);
(2)解:,,
理由如下:,
,
即,
在和中,
,
,
,,
,,
,
.
【知识点】三角形内角和定理;三角形全等及其性质;三角形全等的判定-SAS
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
