2023~2024学年河南安阳龙安区龙安高级中学高一上学期期中数学试卷(PDF版含解析)
文档属性
| 名称 | 2023~2024学年河南安阳龙安区龙安高级中学高一上学期期中数学试卷(PDF版含解析) |

|
|
| 格式 | |||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-12 00:00:00 | ||
图片预览




文档简介
2023~2024学年河南安阳龙安区龙安高级中学高一上学期期中数学试卷
一、单选题(本大题共8小题,每小题5分,共40分)
1、已知集合 , ,则 的子集的个数为( )
A.2
B.4
C.7
D.8
2、下列函数中,既是奇函数又是增函数的是( )
2
A. =
B. = +1
C. = 3
D. = 2
3、设 ,则“ ”是“ ”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
4、已知命题p: , ,则 为( )
A.
B.
C.
D.
5、下列结论正确的是( )
A.若 ,则
B.若 ,则
C.若 ,则
D.若 ,则
6、函数 的定义域为
A.
B.
C.
D.
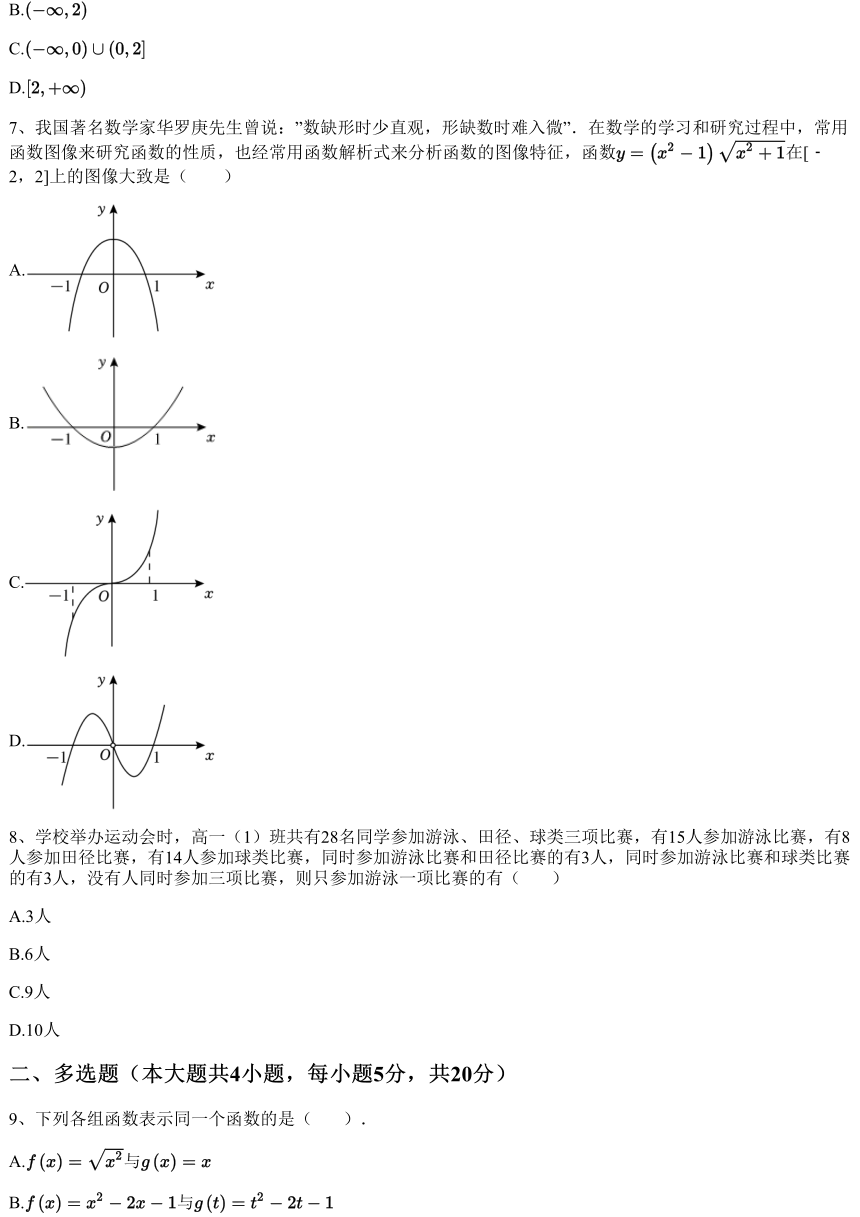
7、我国著名数学家华罗庚先生曾说:”数缺形时少直观,形缺数时难入微”.在数学的学习和研究过程中,常用
函数图像来研究函数的性质,也经常用函数解析式来分析函数的图像特征,函数 在[﹣
2,2]上的图像大致是( )
A.
B.
C.
D.
8、学校举办运动会时,高一(1)班共有28名同学参加游泳、田径、球类三项比赛,有15人参加游泳比赛,有8
人参加田径比赛,有14人参加球类比赛,同时参加游泳比赛和田径比赛的有3人,同时参加游泳比赛和球类比赛
的有3人,没有人同时参加三项比赛,则只参加游泳一项比赛的有( )
A.3人
B.6人
C.9人
D.10人
二、多选题(本大题共4小题,每小题5分,共20分)
9、下列各组函数表示同一个函数的是( ).
A. 与
B. 与
C. 与
D. 与
10、下列函数中,值域为 的是( )
A. ,
B.
C. ,
D.
11、关于函数 ,下列说法正确的是( )
A. 定义域为
B. 的值域为
C.在定义域上单调递减
D.图象关于原点对称
12、下列说法正确的为( )
A.对任意实数 ,
B.
C.函数 的图象在 的图象的上方
D.函数 的最小值为
三、填空题(本大题共4小题,每小题5分,共20分)
13、已知函数 ( )是定义在R上的奇函数,当 ( ,0)时, ( )=2 3+ ,则 (2)= .
14、如果函数 在区间 上是减函数,则实数a的取值范围是 .
15、函数 且 必过定点 .
16、已知幂函数 是偶函数且满足对任意 , 有 ,请写出 的
一个表达式 .
四、解答题(本大题共6小题,共70分)
17、(本小题10分)
已知函数 的定义域为A,集合 .
(1)当 时,求 ( );
(2)若 ,求a的取值范围.
18、(本小题12分)
已知函数 .
(1)求 ;
(2)若 ,求 的值.
19、(本小题12分)
已知关于 的不等式 .
(1)若不等式的解集为 或 ,求 的值.
(2) 关于 的不等式 恒成立,求 的取值范围.
20、(本小题12分)
(1)设 ,求 的最小值;
(2)已知 , , ,求 的取值范围.
21、(本小题12分)
已知函数 是定义在 上的奇函数,且 .
(1)确定函数 的解析式;
(2)用定义证明 在 上是增函数;
(3)解不等式: .
22、(本小题12分)
吉祥物“冰墩墩”在北京 年冬奥会强势出圈,并衍生出很多不同品类的吉祥物手办.某企业承接了“冰墩
墩”玩具手办的生产,已知生产此玩具手办的固定成本为 万元.每生产 万盒,需投入成本 万元,当产
量小于或等于 万盒时 ;当产量大于 万盒时 ,若每盒玩具手办售
价 元,通过市场分析,该企业生产的玩具手办可以全部销售完(利润=售价-成本,成本=固定成本+生产
中投入成本)
(1)求“冰墩墩” 玩具手办销售利润 (万元)关于产量 (万盒)的函数关系式;
(2)当产量为多少万盒时,该企业在生产中所获利润最大?
参考答案
一、单选题
1、
<答 案>:
D
<解析>:
因为 , ,
所以 .
则 的子集有 , , , , , , , ,共8个.
故选:D.
2、
<答 案>:
C
<解析>:
2
解:对于A: = 为奇函数,但是函数在 ,0 和 0,+ 上单调递减,在定义域上不具有单调性,故A有误;
对于B: = +1为非奇非偶函数,在定义域上单调递减,故B有误;
C = 3 对于 : 为奇函数,且在定义域上单调递增,故C无误;
D = 2 对于 : 为偶函数,在 ,0 上单调递增,在 0,+ 上单调递减,故D有误;
因此正确答案为:C
3、
<答 案>:
A
<解析>:
解不等式 得 , 可以得到 ,但 不能说明 ,所以“ ”是“ ”的充分不
必要条件.
故选:A.
4、
<答 案>:
B
<解析>:
因为存在命题的否定是全称命题,
所以 为 ,
故选:B
5、
<答 案>:
C
<解析>:
A.当 ,有 ,若 ,则 ,故A错误;
B.若 ,则 ,故B错误;
C.若 ,则 ,则 ,故C正确;
D.若 ,则 ,故D错误.
故选:C
6、
<答 案>:
C
<解析>:
由题意得: 得: 且 , 定义域为 .故选:C.
7、
<答 案>:
B
<解析>:
定义域为R,
,
则 是偶函数,其图象关于y轴轴对称,排除选项CD;
又因为 ,则排除选项A,选B.
因此正确答案为:B .
8、
<答 案>:
C
<解析>:
由题意只参加游泳比赛的人数 ;
故选:C.
二、多选题
9、
<答 案>:
B;C
<解析>:
选项A,当 时, , ,
所以 与 对应关系不完全一致 ,故不是同一个函数;
选项B, 与 定义域都为 ,
且对应关系完全一致,故是同一个函数;
选项C, 与 的定义域都为 ,
且 ,对应关系完全一致,故是同一个函数;
选项D,对 ,由 ,解得 ,
所以 的定义域为 ,
对 ,由 ,解得 或 ,
所以 的定义域为 ,
两函数定义域不同,故不是同一个函数.
故选:BC.
10、
<答案 >:
A;C
<解析>:
对于A:函数 , 在定义域上单调递增,
又 , ,所以 ,故A正确;
对于B:由 ,所以 ,即 ,故B错误;
对于C:函数 , 在定义域上单调递增,
又 , ,所以 ,故C正确;
对于D:因为 ,所以 ,当且仅当 ,即 时取等号,
所以 ,故D错误;
故选:AC
11、
<答案 >:
B;D
<解析>:
解:函数 的定义域为 ,
又 ,所以 在定义域上是奇函数,
图象关于原点对称,
又 都在 上递减,则 在 和 上递减,
当 时, ,当 时, ,
所以 在定义域上是奇函数知: 的值域为 ,
故选:BD
12、
<答案 >:
B;D
<解析>:
对于A,当 时, 无意义,A有误;
对于B, , , 在 上单调递增, ;
在 上单调递增, , ,B无误;
对于C,当 时, ,C有误;
对于D, , (当且仅当 ,即 时取等号),
,D无误.
因此正确 答案为:BD.
三、填空题
13、
<答案 >:
18
<解析>:
函数 是定义在R上的奇函数, = ,则 = ,
2 = 2 = 2 2 3+ 2 =18.
因此正确答案为:18
14、
<答案 >:
<解析>:
函数 在区间 上是减函数,∴ ,则 故答案为:
15、
<答案 >:
<解析>:
令x﹣2=0,即x=2,可得f(2)=a0+2=3,
可得函数的图象经过点(2,3),
因此正确答案为(2,3).
16、
<答案 >:
或 (答案不唯一)
<解析>:
因为对任意 , 有 ,
所以 在 上是递减函数,
所以幂函数 是偶函数且在 上递减.
从而 可以是 或 .
故答案为: 或 (答案 不唯一)
四、解答题
17、
<答案 >:
(1) 或
(2) |
<解析>:
(1)要使函数 有意义,则 ,解得: ,
所以集合 | .
,
∴ ,
∴ 或 ,
∴ 或 ;
(2) ,
①当 时, ,即 ,满足题意;
②当 时,由 ,得 ,解得: ,
综上所述:a的取值范围为 .
18、
<答案 >:
(1)
(2) 或 .
<解析>:
(1)由题意知, ,所以 .
(2)因为 ,所以当 时, ,所以 ,不满足 舍去;
当 时, ,所以 ,符合题意;
当 时, ,解得 或 舍去,所以 .
综上,当 时, 或 .
19、
<答案 >:
(1) ;
(2) .
<解析>:
(1)由韦达定理即可求解;
(2)二次项系数为负,且判 别式小于0即可.
(1)
若不等式 的解集为 或 ,
则 和 是方程 的两个实数根;
由韦达定理可知: ,
解得 .
(2)
关于 的不等式 恒成立,
则有 且 ,
解得: .
20、
<答案 >:
(1) ;(2) .
<解析>:
(1)∵ ,所以 ,
∴ ,
当且仅当 ,即 时等号成立,
∴ 的最小值为 .
(2)∵ , , ,
∴
当且仅当 时,即 , 时,等号成立,
∴ 的取值范围为 .
21、
<答案 >:
(1)
(2)证明见解析
(3)
<解析>:
(1)由题意,得 ,
∴ (经检验符合题意),故 .
(2)证明 任取 ,且 ,
则 .
∵ ,∴ , , .
又 ,∴ .∴ ,即 ,
∴ 在 上是增函数.
(3)由(2)知 在 上是增函数,又 在 上为奇函数,
,∴ ,∴ ,
解得 .∴不等式的解集为 .
22、
<答案 >:
(1) ,
(2) 万盒
<解析>:
(1)当产量小于或等于50万盒时, ,
当产量大于50万盒时, ,
故销售利润y(万元)关于产量x(万盒)的函数关系式为
,
(2)当 时, 在 上为增函数,所以 ;
当 时, ,对称轴为 ,
所以 在 上为增函数, 减函数,
则 时, 取到最大值为1200.
因为700 1200,所以当产量为70万盒时,该企业所获利润最 大.
一、单选题(本大题共8小题,每小题5分,共40分)
1、已知集合 , ,则 的子集的个数为( )
A.2
B.4
C.7
D.8
2、下列函数中,既是奇函数又是增函数的是( )
2
A. =
B. = +1
C. = 3
D. = 2
3、设 ,则“ ”是“ ”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
4、已知命题p: , ,则 为( )
A.
B.
C.
D.
5、下列结论正确的是( )
A.若 ,则
B.若 ,则
C.若 ,则
D.若 ,则
6、函数 的定义域为
A.
B.
C.
D.
7、我国著名数学家华罗庚先生曾说:”数缺形时少直观,形缺数时难入微”.在数学的学习和研究过程中,常用
函数图像来研究函数的性质,也经常用函数解析式来分析函数的图像特征,函数 在[﹣
2,2]上的图像大致是( )
A.
B.
C.
D.
8、学校举办运动会时,高一(1)班共有28名同学参加游泳、田径、球类三项比赛,有15人参加游泳比赛,有8
人参加田径比赛,有14人参加球类比赛,同时参加游泳比赛和田径比赛的有3人,同时参加游泳比赛和球类比赛
的有3人,没有人同时参加三项比赛,则只参加游泳一项比赛的有( )
A.3人
B.6人
C.9人
D.10人
二、多选题(本大题共4小题,每小题5分,共20分)
9、下列各组函数表示同一个函数的是( ).
A. 与
B. 与
C. 与
D. 与
10、下列函数中,值域为 的是( )
A. ,
B.
C. ,
D.
11、关于函数 ,下列说法正确的是( )
A. 定义域为
B. 的值域为
C.在定义域上单调递减
D.图象关于原点对称
12、下列说法正确的为( )
A.对任意实数 ,
B.
C.函数 的图象在 的图象的上方
D.函数 的最小值为
三、填空题(本大题共4小题,每小题5分,共20分)
13、已知函数 ( )是定义在R上的奇函数,当 ( ,0)时, ( )=2 3+ ,则 (2)= .
14、如果函数 在区间 上是减函数,则实数a的取值范围是 .
15、函数 且 必过定点 .
16、已知幂函数 是偶函数且满足对任意 , 有 ,请写出 的
一个表达式 .
四、解答题(本大题共6小题,共70分)
17、(本小题10分)
已知函数 的定义域为A,集合 .
(1)当 时,求 ( );
(2)若 ,求a的取值范围.
18、(本小题12分)
已知函数 .
(1)求 ;
(2)若 ,求 的值.
19、(本小题12分)
已知关于 的不等式 .
(1)若不等式的解集为 或 ,求 的值.
(2) 关于 的不等式 恒成立,求 的取值范围.
20、(本小题12分)
(1)设 ,求 的最小值;
(2)已知 , , ,求 的取值范围.
21、(本小题12分)
已知函数 是定义在 上的奇函数,且 .
(1)确定函数 的解析式;
(2)用定义证明 在 上是增函数;
(3)解不等式: .
22、(本小题12分)
吉祥物“冰墩墩”在北京 年冬奥会强势出圈,并衍生出很多不同品类的吉祥物手办.某企业承接了“冰墩
墩”玩具手办的生产,已知生产此玩具手办的固定成本为 万元.每生产 万盒,需投入成本 万元,当产
量小于或等于 万盒时 ;当产量大于 万盒时 ,若每盒玩具手办售
价 元,通过市场分析,该企业生产的玩具手办可以全部销售完(利润=售价-成本,成本=固定成本+生产
中投入成本)
(1)求“冰墩墩” 玩具手办销售利润 (万元)关于产量 (万盒)的函数关系式;
(2)当产量为多少万盒时,该企业在生产中所获利润最大?
参考答案
一、单选题
1、
<答 案>:
D
<解析>:
因为 , ,
所以 .
则 的子集有 , , , , , , , ,共8个.
故选:D.
2、
<答 案>:
C
<解析>:
2
解:对于A: = 为奇函数,但是函数在 ,0 和 0,+ 上单调递减,在定义域上不具有单调性,故A有误;
对于B: = +1为非奇非偶函数,在定义域上单调递减,故B有误;
C = 3 对于 : 为奇函数,且在定义域上单调递增,故C无误;
D = 2 对于 : 为偶函数,在 ,0 上单调递增,在 0,+ 上单调递减,故D有误;
因此正确答案为:C
3、
<答 案>:
A
<解析>:
解不等式 得 , 可以得到 ,但 不能说明 ,所以“ ”是“ ”的充分不
必要条件.
故选:A.
4、
<答 案>:
B
<解析>:
因为存在命题的否定是全称命题,
所以 为 ,
故选:B
5、
<答 案>:
C
<解析>:
A.当 ,有 ,若 ,则 ,故A错误;
B.若 ,则 ,故B错误;
C.若 ,则 ,则 ,故C正确;
D.若 ,则 ,故D错误.
故选:C
6、
<答 案>:
C
<解析>:
由题意得: 得: 且 , 定义域为 .故选:C.
7、
<答 案>:
B
<解析>:
定义域为R,
,
则 是偶函数,其图象关于y轴轴对称,排除选项CD;
又因为 ,则排除选项A,选B.
因此正确答案为:B .
8、
<答 案>:
C
<解析>:
由题意只参加游泳比赛的人数 ;
故选:C.
二、多选题
9、
<答 案>:
B;C
<解析>:
选项A,当 时, , ,
所以 与 对应关系不完全一致 ,故不是同一个函数;
选项B, 与 定义域都为 ,
且对应关系完全一致,故是同一个函数;
选项C, 与 的定义域都为 ,
且 ,对应关系完全一致,故是同一个函数;
选项D,对 ,由 ,解得 ,
所以 的定义域为 ,
对 ,由 ,解得 或 ,
所以 的定义域为 ,
两函数定义域不同,故不是同一个函数.
故选:BC.
10、
<答案 >:
A;C
<解析>:
对于A:函数 , 在定义域上单调递增,
又 , ,所以 ,故A正确;
对于B:由 ,所以 ,即 ,故B错误;
对于C:函数 , 在定义域上单调递增,
又 , ,所以 ,故C正确;
对于D:因为 ,所以 ,当且仅当 ,即 时取等号,
所以 ,故D错误;
故选:AC
11、
<答案 >:
B;D
<解析>:
解:函数 的定义域为 ,
又 ,所以 在定义域上是奇函数,
图象关于原点对称,
又 都在 上递减,则 在 和 上递减,
当 时, ,当 时, ,
所以 在定义域上是奇函数知: 的值域为 ,
故选:BD
12、
<答案 >:
B;D
<解析>:
对于A,当 时, 无意义,A有误;
对于B, , , 在 上单调递增, ;
在 上单调递增, , ,B无误;
对于C,当 时, ,C有误;
对于D, , (当且仅当 ,即 时取等号),
,D无误.
因此正确 答案为:BD.
三、填空题
13、
<答案 >:
18
<解析>:
函数 是定义在R上的奇函数, = ,则 = ,
2 = 2 = 2 2 3+ 2 =18.
因此正确答案为:18
14、
<答案 >:
<解析>:
函数 在区间 上是减函数,∴ ,则 故答案为:
15、
<答案 >:
<解析>:
令x﹣2=0,即x=2,可得f(2)=a0+2=3,
可得函数的图象经过点(2,3),
因此正确答案为(2,3).
16、
<答案 >:
或 (答案不唯一)
<解析>:
因为对任意 , 有 ,
所以 在 上是递减函数,
所以幂函数 是偶函数且在 上递减.
从而 可以是 或 .
故答案为: 或 (答案 不唯一)
四、解答题
17、
<答案 >:
(1) 或
(2) |
<解析>:
(1)要使函数 有意义,则 ,解得: ,
所以集合 | .
,
∴ ,
∴ 或 ,
∴ 或 ;
(2) ,
①当 时, ,即 ,满足题意;
②当 时,由 ,得 ,解得: ,
综上所述:a的取值范围为 .
18、
<答案 >:
(1)
(2) 或 .
<解析>:
(1)由题意知, ,所以 .
(2)因为 ,所以当 时, ,所以 ,不满足 舍去;
当 时, ,所以 ,符合题意;
当 时, ,解得 或 舍去,所以 .
综上,当 时, 或 .
19、
<答案 >:
(1) ;
(2) .
<解析>:
(1)由韦达定理即可求解;
(2)二次项系数为负,且判 别式小于0即可.
(1)
若不等式 的解集为 或 ,
则 和 是方程 的两个实数根;
由韦达定理可知: ,
解得 .
(2)
关于 的不等式 恒成立,
则有 且 ,
解得: .
20、
<答案 >:
(1) ;(2) .
<解析>:
(1)∵ ,所以 ,
∴ ,
当且仅当 ,即 时等号成立,
∴ 的最小值为 .
(2)∵ , , ,
∴
当且仅当 时,即 , 时,等号成立,
∴ 的取值范围为 .
21、
<答案 >:
(1)
(2)证明见解析
(3)
<解析>:
(1)由题意,得 ,
∴ (经检验符合题意),故 .
(2)证明 任取 ,且 ,
则 .
∵ ,∴ , , .
又 ,∴ .∴ ,即 ,
∴ 在 上是增函数.
(3)由(2)知 在 上是增函数,又 在 上为奇函数,
,∴ ,∴ ,
解得 .∴不等式的解集为 .
22、
<答案 >:
(1) ,
(2) 万盒
<解析>:
(1)当产量小于或等于50万盒时, ,
当产量大于50万盒时, ,
故销售利润y(万元)关于产量x(万盒)的函数关系式为
,
(2)当 时, 在 上为增函数,所以 ;
当 时, ,对称轴为 ,
所以 在 上为增函数, 减函数,
则 时, 取到最大值为1200.
因为700 1200,所以当产量为70万盒时,该企业所获利润最 大.
同课章节目录
