高中数学人教A版:函数的概念 课件(共16张PPT)
文档属性
| 名称 | 高中数学人教A版:函数的概念 课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-12 12:54:19 | ||
图片预览





文档简介
(共16张PPT)
3.1.1函数的概念
人教A版必修第一册高一数学
(1)正方形的周长与边长x的对应关系是l=4x;
(2)正比例函数:l=4x;
上述两个函数,是相同的函数吗
探究引入
0R
思考
数学建构
情境1某“复兴号”高速列车加速到350km/h后保持匀速运行半小时.
问题1:在这半小时内,列车行进的路程S ( 单 位 :km) 与运行时间t ( 单 位 :h) 的关系式 如何表示 S=350t ①
追 问:S 是t的函数吗 对于每一个确定的t 都有唯一的S与之相对应.
S是t的函数.
问题2:这趟列车加速到350 km/h 后,运行1h就前进了350km吗
不是,要注意t的范围.
追问1:那么我们如何更精确地表示S和t的对应关系呢
给出t 和S 的变化范围.
集合A 集合B
对于 数集A 中的任一元素t, 按 照 对应关系①, 在 数集B_中都有唯一确定的元素S和它相对应。
变量x→变量y 集合A →集合B
情境1某“复兴号”高速列车加速到350km/h后保持匀速运行半小时.
S=350t ①
问题2追问2:变 量t和S的取值范围该如何表示
A ={1|0≤≤0.5} B={S|0≤S≤175}
问 题 3 :集 合A 和B 中的元素有什么关系 集合A 对应关系
集合B
数学建构
数学建构
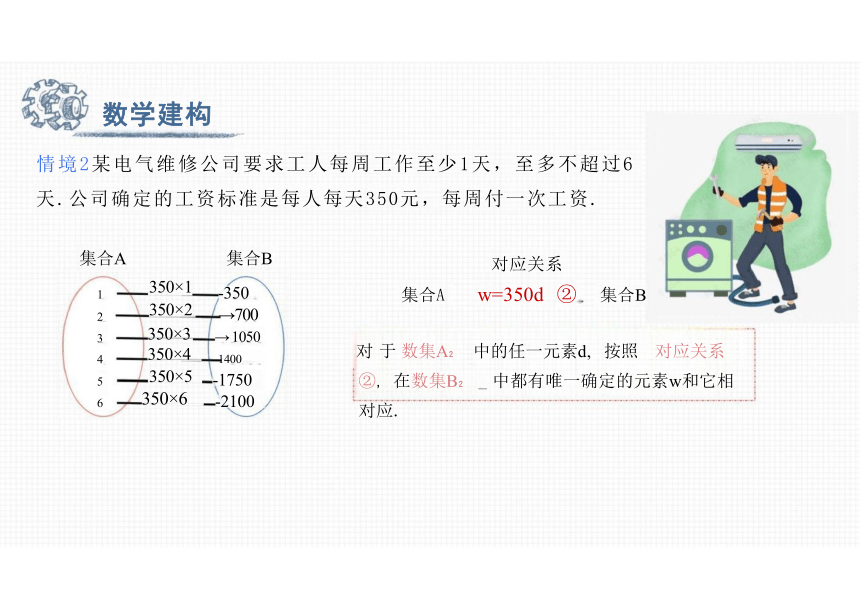
情境2某电气维修公司要求工人每周工作至少1天,至多不超过6 天.公司确定的工资标准是每人每天350元,每周付一次工资.
问题4 :一个工人的工资w (单位:元)是他工作天数d的函数吗 如果是, 请写出w和d的对应关系式.
w=350d ②
问题5:变量d和w的取值范围如何表示
A ={1,2,3,4,5,6} B ={350,700,1050,1400,1750,2100}
对于每一个确定的d都有唯一的w与之相对应.
w是d的函数;
数学建构
情境2某电气维修公司要求工人每周工作至少1天,至多不超过6 天.公司确定的工资标准是每人每天350元,每周付一次工资.
对应关系
集合A w=350d ② 集合B
对 于 数集A 中的任一元素d, 按照 对应关系②, 在数集B _ 中都有唯一确定的元素w和它相对应.
350×1
350×2
350×3 350×4
350×5
350×6
-350
→700
→ 1050
1400
-1750
-2100
集合A 集合B
1
2
3
4
5
6
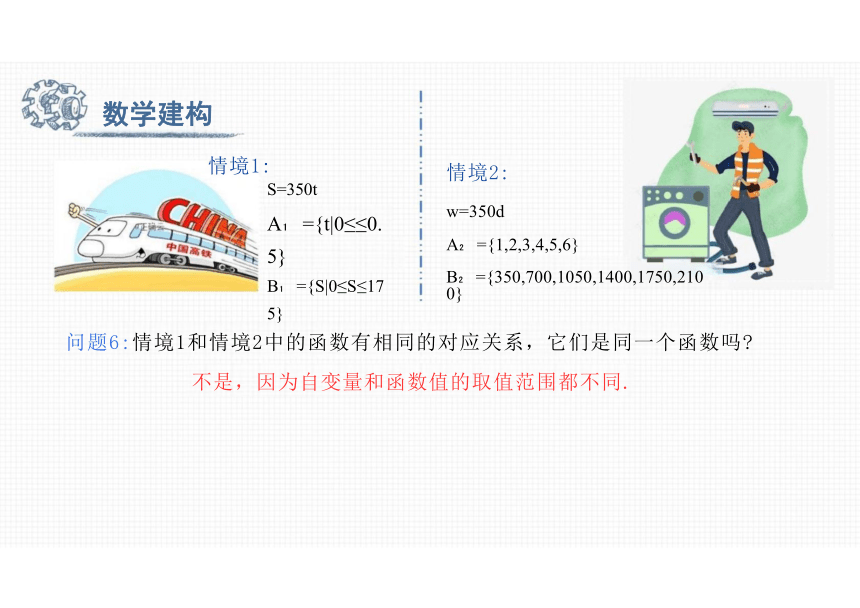
问题6:情境1和情境2中的函数有相同的对应关系,它们是同一个函数吗
不是,因为自变量和函数值的取值范围都不同.
情境2:
w=350d
A ={1,2,3,4,5,6}
B ={350,700,1050,1400,1750,2100}
情境1:
S=350t
A ={t|0≤≤0.5} B ={S|0≤S≤175}
数学建构
数学建构
情境3下图是某日的空气质量指数(Air Quality Index,简称AQI) 变化图
问题7:你能在图中找到任一时刻的 AQI的值吗 可以
问题8:AQI的值I是任一时刻的函数
问题9:你知道这一天内任一时刻t和 AQI的值I的变化范围吗 请用A 、B 表示.
A ={1|0≤≤24}B ={1|0对于 数集A 中的任一元素t, 按照图3.1-1的对应关系,
在 数集B 中都有唯一确定的元素I和它相对应.
追 问 :此情景中,I 与t 的对应关
08:00 to 12:00
图3.1-1
系是如何表示的
100
50
0
16:00 20:00 24:00
北京空气质量指数
图3.1-1
是!
良 优
轻度污染
吗
04:00
150
数学建构
情境4国际上常用恩格尔系数r 反应一个地区人民生
活质量的高低,恩格尔系数越低,生活质量越高.下表是我国城镇居民恩格尔系数 变化情况.
表3.1-1
问题10:恩格尔系数r是年份y的函数吗 请写出y和r的取值范围,用A 、B 表示.
是 !A ={2006,2007,2008,2009,2010,2011,2012,2013,2014,2015} B ={r|0<≤1}
追 问 :此情景中,y 与r的对应关系是如何表示的
表3.1-1
年份y 2006 2007 2008 2009 2010 2011 2012 2013 2014
2015
恩格尔系数r (%) 36.69 36.81 38.17 35.69 35.15 33.53 33.87 29.89 29.35
28.57
数学建构
情境4国际上常用恩格尔系数r 反应一个地区人民生
活质量的高低,恩格尔系数越低,生活质量越高.下表是我国城镇居民恩格尔系数 变化情况.
年份y 2006 2007 2008 2009 2010 2011 2012 2013 2014
2015
恩格尔系数r (%) 36.69 36.81 38.17 35.69 35.15 33.53 33.87 29.89 29.35
28.57
表3.1-1
对于 数集A 中的任一元素y, 按 照表3.1-1的对应关系 在 数集B 中都有唯一确定的元素r和它相对应.
集合A 对应关系 集合B
情境1 A B
情境2
情境3
情境4
数学建构
问题11:以上四个函数有什么共同特征
思考:函数的值域与集合B有什
么关系
定义域:自变量x的取值范围A;
值域:与x相对应的y值叫做函数值,函数值的集合{f(x)|x∈A}.
一般地,设A,B 是非空的 实数集,如果对于集合A中 的任意 一 个数x,
按照某种确定的对应关系f, 在集合B中 都 有唯 一确定的数y和它对应,那么 就称f:A→B 为从集合A到集合B的一个函数 (function).
数学建构
记作:y=f(x),x∈A
函数的概念:
数学建构
情境2:w=350d
情境1:S=350t A ={t|0≤t≤0.5}B ={S|0≤S≤175 }
A ={1,2,3,4,5,6}
B ={350,700,1050,1400, 1750,2100}
值 域
情境3:
年份y 2006 2007 2008 2009 2010 2011 2012 2013 2014
2015
恩格尔系数r (%) 36.69 36.81 38.17 35.69 35.15 33.53 33.87 29.89 29.35
28.57
A ={2006,2007,2008,2009,2010,2011,
2012,2013,2014,2015}
B ={r|0值域C ={36.69,36.81,38.17,35.69,35.15,33.53, 33.87,29.89,29.35,28.57}
一般地,设A,B 是非空的 实数集,如果对于集合A中的任意 一 个数x,
按照某种确定的对应关系f, 在集合B中都有唯 一确定的数y和它对应,那么 就称f:A→B 为从集合A到集合B的一个函数 (function).
定义域:自变量x的取值范围A;
值域:与x相对应的y值叫做函数值的集合{f(x)|x∈A}.
函数三要素:
定义域、值域、对应关系
数学建构
函数的定义:
记作:y=f(x)
创设情境 提出问题 初中函数定义 判断依据 推理归纳 生成概念 数学抽象
函数三要素:
[定义域 值域
对应关系
一般地,设A,B 是非空的 实 数 集,如果对于集合A中的任 意一 个数x , 按照某种确定的对应关系f, 在集合B中都有唯 一确定的数y和它对应,那么 就称f:A→B 为从集合A到集合B的一个函数 (function).
课堂小结
THANKS
课后作业:函数的概念练习
3.1.1函数的概念
人教A版必修第一册高一数学
(1)正方形的周长与边长x的对应关系是l=4x;
(2)正比例函数:l=4x;
上述两个函数,是相同的函数吗
探究引入
0R
思考
数学建构
情境1某“复兴号”高速列车加速到350km/h后保持匀速运行半小时.
问题1:在这半小时内,列车行进的路程S ( 单 位 :km) 与运行时间t ( 单 位 :h) 的关系式 如何表示 S=350t ①
追 问:S 是t的函数吗 对于每一个确定的t 都有唯一的S与之相对应.
S是t的函数.
问题2:这趟列车加速到350 km/h 后,运行1h就前进了350km吗
不是,要注意t的范围.
追问1:那么我们如何更精确地表示S和t的对应关系呢
给出t 和S 的变化范围.
集合A 集合B
对于 数集A 中的任一元素t, 按 照 对应关系①, 在 数集B_中都有唯一确定的元素S和它相对应。
变量x→变量y 集合A →集合B
情境1某“复兴号”高速列车加速到350km/h后保持匀速运行半小时.
S=350t ①
问题2追问2:变 量t和S的取值范围该如何表示
A ={1|0≤≤0.5} B={S|0≤S≤175}
问 题 3 :集 合A 和B 中的元素有什么关系 集合A 对应关系
集合B
数学建构
数学建构
情境2某电气维修公司要求工人每周工作至少1天,至多不超过6 天.公司确定的工资标准是每人每天350元,每周付一次工资.
问题4 :一个工人的工资w (单位:元)是他工作天数d的函数吗 如果是, 请写出w和d的对应关系式.
w=350d ②
问题5:变量d和w的取值范围如何表示
A ={1,2,3,4,5,6} B ={350,700,1050,1400,1750,2100}
对于每一个确定的d都有唯一的w与之相对应.
w是d的函数;
数学建构
情境2某电气维修公司要求工人每周工作至少1天,至多不超过6 天.公司确定的工资标准是每人每天350元,每周付一次工资.
对应关系
集合A w=350d ② 集合B
对 于 数集A 中的任一元素d, 按照 对应关系②, 在数集B _ 中都有唯一确定的元素w和它相对应.
350×1
350×2
350×3 350×4
350×5
350×6
-350
→700
→ 1050
1400
-1750
-2100
集合A 集合B
1
2
3
4
5
6
问题6:情境1和情境2中的函数有相同的对应关系,它们是同一个函数吗
不是,因为自变量和函数值的取值范围都不同.
情境2:
w=350d
A ={1,2,3,4,5,6}
B ={350,700,1050,1400,1750,2100}
情境1:
S=350t
A ={t|0≤≤0.5} B ={S|0≤S≤175}
数学建构
数学建构
情境3下图是某日的空气质量指数(Air Quality Index,简称AQI) 变化图
问题7:你能在图中找到任一时刻的 AQI的值吗 可以
问题8:AQI的值I是任一时刻的函数
问题9:你知道这一天内任一时刻t和 AQI的值I的变化范围吗 请用A 、B 表示.
A ={1|0≤≤24}B ={1|0
在 数集B 中都有唯一确定的元素I和它相对应.
追 问 :此情景中,I 与t 的对应关
08:00 to 12:00
图3.1-1
系是如何表示的
100
50
0
16:00 20:00 24:00
北京空气质量指数
图3.1-1
是!
良 优
轻度污染
吗
04:00
150
数学建构
情境4国际上常用恩格尔系数r 反应一个地区人民生
活质量的高低,恩格尔系数越低,生活质量越高.下表是我国城镇居民恩格尔系数 变化情况.
表3.1-1
问题10:恩格尔系数r是年份y的函数吗 请写出y和r的取值范围,用A 、B 表示.
是 !A ={2006,2007,2008,2009,2010,2011,2012,2013,2014,2015} B ={r|0<≤1}
追 问 :此情景中,y 与r的对应关系是如何表示的
表3.1-1
年份y 2006 2007 2008 2009 2010 2011 2012 2013 2014
2015
恩格尔系数r (%) 36.69 36.81 38.17 35.69 35.15 33.53 33.87 29.89 29.35
28.57
数学建构
情境4国际上常用恩格尔系数r 反应一个地区人民生
活质量的高低,恩格尔系数越低,生活质量越高.下表是我国城镇居民恩格尔系数 变化情况.
年份y 2006 2007 2008 2009 2010 2011 2012 2013 2014
2015
恩格尔系数r (%) 36.69 36.81 38.17 35.69 35.15 33.53 33.87 29.89 29.35
28.57
表3.1-1
对于 数集A 中的任一元素y, 按 照表3.1-1的对应关系 在 数集B 中都有唯一确定的元素r和它相对应.
集合A 对应关系 集合B
情境1 A B
情境2
情境3
情境4
数学建构
问题11:以上四个函数有什么共同特征
思考:函数的值域与集合B有什
么关系
定义域:自变量x的取值范围A;
值域:与x相对应的y值叫做函数值,函数值的集合{f(x)|x∈A}.
一般地,设A,B 是非空的 实数集,如果对于集合A中 的任意 一 个数x,
按照某种确定的对应关系f, 在集合B中 都 有唯 一确定的数y和它对应,那么 就称f:A→B 为从集合A到集合B的一个函数 (function).
数学建构
记作:y=f(x),x∈A
函数的概念:
数学建构
情境2:w=350d
情境1:S=350t A ={t|0≤t≤0.5}B ={S|0≤S≤175 }
A ={1,2,3,4,5,6}
B ={350,700,1050,1400, 1750,2100}
值 域
情境3:
年份y 2006 2007 2008 2009 2010 2011 2012 2013 2014
2015
恩格尔系数r (%) 36.69 36.81 38.17 35.69 35.15 33.53 33.87 29.89 29.35
28.57
A ={2006,2007,2008,2009,2010,2011,
2012,2013,2014,2015}
B ={r|0
一般地,设A,B 是非空的 实数集,如果对于集合A中的任意 一 个数x,
按照某种确定的对应关系f, 在集合B中都有唯 一确定的数y和它对应,那么 就称f:A→B 为从集合A到集合B的一个函数 (function).
定义域:自变量x的取值范围A;
值域:与x相对应的y值叫做函数值的集合{f(x)|x∈A}.
函数三要素:
定义域、值域、对应关系
数学建构
函数的定义:
记作:y=f(x)
创设情境 提出问题 初中函数定义 判断依据 推理归纳 生成概念 数学抽象
函数三要素:
[定义域 值域
对应关系
一般地,设A,B 是非空的 实 数 集,如果对于集合A中的任 意一 个数x , 按照某种确定的对应关系f, 在集合B中都有唯 一确定的数y和它对应,那么 就称f:A→B 为从集合A到集合B的一个函数 (function).
课堂小结
THANKS
课后作业:函数的概念练习
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
