高中数学人教A版:函数的应用(一) 课件(共25张PPT)
文档属性
| 名称 | 高中数学人教A版:函数的应用(一) 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-12 00:00:00 | ||
图片预览





文档简介
(共25张PPT)
Spanish fu
Great
Depression
20%
Second
oil shock
10%
0%
-10%
-20% 先法能源科技战略情报研究中心
1900 1910 1920 1930 1940 1950 1960 197019801990200020102020
情境创设:生活之源
Global
Financial
Crisis
First
oil shock
Word War ll
30%
情境创设:生活之源
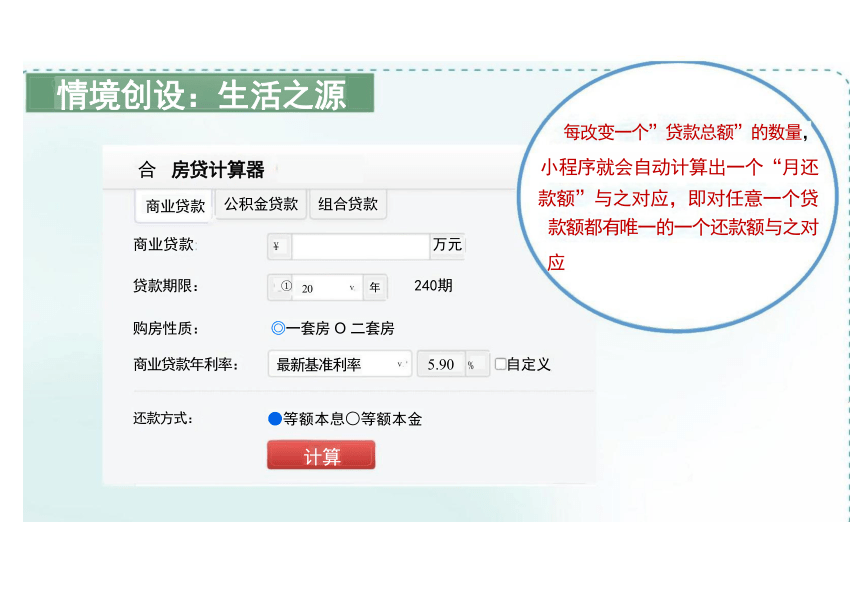
每改变一个”贷款总额”的数量,
合 房贷计算器 小程序就会自动计算出一个“月还
商业贷款 公积金贷款 组合贷款 款额”与之对应,即对任意一个贷
款额都有唯一的一个还款额与之对
商业贷款 万元
应
贷款期限: ① 20 V 年 240期
购房性质: ◎一套房 O 二套房
商业贷款年利率: 最新基准利率 V 5.90 % 自定义
●等额本息○等额本金
计算
还款方式:
函数
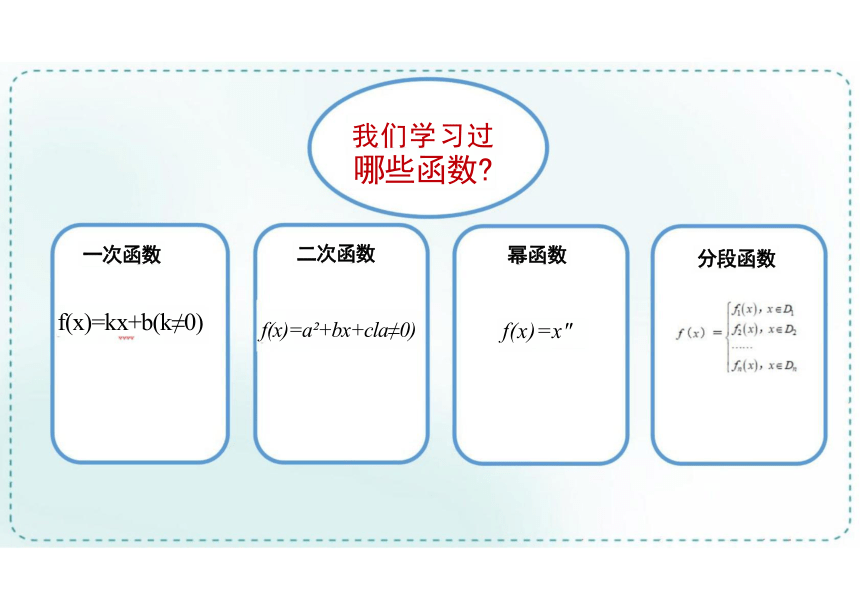
二次函数
f(x)=a +bx+cla≠0)
一次函数
f(x)=kx+b(k≠0)
我们学习过 哪些函数
幂函数
f(x)=x"
分段函数
一次函数
二次函数 幂函数
分段函数
函数 e
函数是数学中的重要思想,也与
我们的生活密不可分,下面就让 我们用函数的思想跟随一名盐田 高级中学的毕业生一起开启她大 学毕业后的生活之旅吧!
一次函数
二次函数
幂函数
分段函数
的应用
函数
刘小宁同学是深圳市盐田高级中学2016届学生,转眼间到了2023年,
她研究生毕业,加入到某电脑公司工作,月薪8000元。步入社会后, 从新手入职,理财投资,生活用水,依法纳税四幕情景剧展示其所
生活的轨迹中无处不蕴含着函数的应用。
建模之旅
该电脑公司在甲、乙两地各有一个分公司,甲分公司有某一
型号电脑6台,乙分公司现有同一型号电脑12台。现A 地某单位
向该公司购买该型号的电脑10台,B地某单位向该公司购买该型号的电脑8台。已
知每台电脑从甲地运往A,B两地运费分别是40元和30元,从乙地运往A,B两地的运
费分别是80元和50元。
(1)设甲地调运x台电脑到B地,该公司运往A,B两地的总运费为y元,求y关于x的
函数解析式;
(2)若总运费不超过1000元,则有几种调运方案
(3)怎样调整方案使运费最低
第一幕:职场新手,经理布置工作任务:
类型1:一次
函数模型的
应用
【例1】 解:(1)设甲地调运x 台 到B 地,则剩下(6-x) 台 电脑调运到A 地;乙地应调运(8-x) 台电脑至B 地,运往A 地12—(8-x)=(x+4) 台电脑.0≤x≤6,x∈N.
则总运费y=30.x+40(6—x)+50(8-x)+80(x+4)=
20x+960,
∴y=20x+960(x∈N, 且0≤x≤6).
(2)若使y≤1000, 即20x+960≤1000, 得x≤2.
又0≤x≤6,x∈N,∴0≤x≤2,x∈N.
∴x=0,1,2, 即能有3种调运方案.
(3)∵y=2x+960 是 R 上的增函数,
又0≤x≤6,x∈N,
∴当x=0 时 ,y 有最小值为960.
∴从甲地运6台到A 地,从乙地运8台到B 地、运4台到 A 地,运费最低为960元.
1.一次函数模型的实际应用
一次函数模型应用时,本着“问什么,设什么,列什么” 这一原则.
2.一次函数的最值求解
一次函数求最值,常转化为求解不等式ax+b≥0(或≤0), 解答时,注意系数a 的正负,也可以结合函数图象或其单调 性来求最值.
构建一次函数模型的规律方法:
经过最初的锻炼,刘小宁已经能轻松解决
一些简单的问题,得到经理的认可。随着 工作的不断进步,工资奖金的增加,盐小 高宁会采用怎样的方式进行理财投资呢 理财投资可是我们每个人的必修课哦。
建模之旅
刘小宁工作了一段时间后,有了一些积蓄,想进行理财投资,根据长期收益
率市场预测,投资债券等稳健型产品的年收益与投资额成正比,其关系如图1;
投资股票等风险型产品的年收益与投资额的算术平方根成正比,其关系如图2.
(1)帮小宁写出两种产品的年收益f(x)和g(x)
的函数关系式;
(2)其家庭现有20万元资金,全部用于理财投
资,问:怎么分配资金能使投资获得最大年收益
,其最大年收益是多少万元 (图1) (图2)
类型2:二次 函数与幂函数 模型的应用
第二幕:生活小有目标,投资也要做好
( 2 ) 设 投 资 债 券 类 产 品x 万 元 ,
则 股 票 类 投 资 为 ( 2 0 -x) 万 元 , 年 收 益 为V 万
元 ,
依 题 意 得 :y=f(x)+g(20-x),
学生们积极参与,不断补充,帮助刘小宁完成 投资计划。
解 : ( 1 ) 可 设f(x)=k x(x≥0),
所以当t=2, 即 x=16万元时,
收益最大,vmx=3万元
t=√20-x,
则x=20-t ,t∈[0.2 √5],
。
g(x)=k √x(x≥0),
·· ··
则
重
二次函数模型的解析式为g(x)=ax +bx+c(a≠0) 在函数建模中,它占有重
要的地位.在根据实际问题建立函数解析式后,可利用配方法、判别式法、 换元法、函数的单调性等方法来求函数的最值,从而解决实际问题中的最值
问题.也可利用换元最终来求函数的最值.
幂函数模型h(x)=x“在函数建模中,使用频率也比较高,主要可以利用单调
性求出最值。
构建二次函数模型与幂函数模型的规律方法
刘小宁每个月负责交自己家和妈妈家的水费,该市居民自来水收费标准如下:每户每月用水不超过4 吨时,每吨为
1.80元,当用水超过4 吨时,超过部分每吨为3.00元,每月自己家、父母家两户共交水费V 元,已知两户该月用
水量分别为5x,3x.
(1 ) V 关于x 的函数关系式
(2)若两户该月共交水费264元,分别求出甲、乙两户该月的用水量.
小组合作,同学们联手为刘小宁和宁妈排忧解难
类型3:分段
函数模型的
应用
第三幕:生活新手小白遇到水费小麻烦
(1)由题意知,x≥0,令5x=4,得 ;令 则当 时 ,y=(5x+3x)×1.8=14.4x,
时,
时,
(2)由于y=fx)在各段区间上均单增,
当 时 重
当
当 时,令24x-9.6=26.4, 得 x=1.5,
所以刘小宁户用水量为5x=7.5 吨,付费
S =4×1.8+3.5×3=17.70 元
宁妈用水量为3x=4.5 吨,付费S =8.7 元.
=24x-9.6,
即得
1.分段函数的“段”一定要分得合理不重不漏
2.分段函数的定义域为对应每一段自变量取值范围的并集.
3.分段函数的值域求法:逐段求函数值的范围,最后比较再下
结论 .
构建分段函数模型的规律方法
德育之效:立德树人,培养优秀人才
第四幕:依法纳税,履行公民义务
依法纳税是每个公民应尽的义务,个人取得的所得应依照《中华人民共和国个人所得税法》向国
家缴纳个人所得税(简称个税).2019 年1 月1日起,个税税额根据应纳税所得额、税率和速算扣除
数确定,计算公式为个税税额=应纳税所得额×税率-速算扣除数.应纳税所得额的计算公式为应纳税所
得额=综合所得收入额-基本减除费用-专项扣除-专项附加扣除-依法确定的其他扣除.其中,“基本减除
费 用”(免征额)为每年60000元,税率与速算扣除数见表
级 数 全年应纳税所得 额所在区间 税 率 ( % )
速算扣除
数
1 [0.36000] 3
0
2 (36000,144000)| 10
2520
3 [144000,300000] 20
16920
4 [300000.420000] 25
31920
5 (420000.660000) 30
52920
6 (660000,960000) 35
85920
7 (960000,+00) 45
181920
结合3.1.2例8的解析式,应缴纳综合所得个税税额y 关全年综合所得收入额为x(单位:
元)的函数解析式为
(1)如果小王全年的综合所得由189600 元增加到249600元,那么他全年应缴纳多少
综合所得个税
1、理解问题
2、简化假设
3、构建数学(函数)模型
4、求解模型
5、检验模型
6、评价与应用
建模的主要步骤:
课堂小结
1.解有关函数的应用题,首先应考虑选择哪一种函数作为模型,然后
建立其解析式.求解析式时, 一般利用待定系数法,要充分挖掘题目的
隐含条件,充分利用函数图形的直观性.
2 .数学建模的过程图示如下:
实际问题 数学对象 数学模型
推理或
演算
实际问题的解 数学模型的解
解释
评价
数学建模
的过程图示如下:
一次函数
二次函数
幂函数
分段函数
板书设计
函数
数学对象
数学模型
应用
实际问题的解
实际题
数学模型的解
评价 解释
推或
Spanish fu
Great
Depression
20%
Second
oil shock
10%
0%
-10%
-20% 先法能源科技战略情报研究中心
1900 1910 1920 1930 1940 1950 1960 197019801990200020102020
情境创设:生活之源
Global
Financial
Crisis
First
oil shock
Word War ll
30%
情境创设:生活之源
每改变一个”贷款总额”的数量,
合 房贷计算器 小程序就会自动计算出一个“月还
商业贷款 公积金贷款 组合贷款 款额”与之对应,即对任意一个贷
款额都有唯一的一个还款额与之对
商业贷款 万元
应
贷款期限: ① 20 V 年 240期
购房性质: ◎一套房 O 二套房
商业贷款年利率: 最新基准利率 V 5.90 % 自定义
●等额本息○等额本金
计算
还款方式:
函数
二次函数
f(x)=a +bx+cla≠0)
一次函数
f(x)=kx+b(k≠0)
我们学习过 哪些函数
幂函数
f(x)=x"
分段函数
一次函数
二次函数 幂函数
分段函数
函数 e
函数是数学中的重要思想,也与
我们的生活密不可分,下面就让 我们用函数的思想跟随一名盐田 高级中学的毕业生一起开启她大 学毕业后的生活之旅吧!
一次函数
二次函数
幂函数
分段函数
的应用
函数
刘小宁同学是深圳市盐田高级中学2016届学生,转眼间到了2023年,
她研究生毕业,加入到某电脑公司工作,月薪8000元。步入社会后, 从新手入职,理财投资,生活用水,依法纳税四幕情景剧展示其所
生活的轨迹中无处不蕴含着函数的应用。
建模之旅
该电脑公司在甲、乙两地各有一个分公司,甲分公司有某一
型号电脑6台,乙分公司现有同一型号电脑12台。现A 地某单位
向该公司购买该型号的电脑10台,B地某单位向该公司购买该型号的电脑8台。已
知每台电脑从甲地运往A,B两地运费分别是40元和30元,从乙地运往A,B两地的运
费分别是80元和50元。
(1)设甲地调运x台电脑到B地,该公司运往A,B两地的总运费为y元,求y关于x的
函数解析式;
(2)若总运费不超过1000元,则有几种调运方案
(3)怎样调整方案使运费最低
第一幕:职场新手,经理布置工作任务:
类型1:一次
函数模型的
应用
【例1】 解:(1)设甲地调运x 台 到B 地,则剩下(6-x) 台 电脑调运到A 地;乙地应调运(8-x) 台电脑至B 地,运往A 地12—(8-x)=(x+4) 台电脑.0≤x≤6,x∈N.
则总运费y=30.x+40(6—x)+50(8-x)+80(x+4)=
20x+960,
∴y=20x+960(x∈N, 且0≤x≤6).
(2)若使y≤1000, 即20x+960≤1000, 得x≤2.
又0≤x≤6,x∈N,∴0≤x≤2,x∈N.
∴x=0,1,2, 即能有3种调运方案.
(3)∵y=2x+960 是 R 上的增函数,
又0≤x≤6,x∈N,
∴当x=0 时 ,y 有最小值为960.
∴从甲地运6台到A 地,从乙地运8台到B 地、运4台到 A 地,运费最低为960元.
1.一次函数模型的实际应用
一次函数模型应用时,本着“问什么,设什么,列什么” 这一原则.
2.一次函数的最值求解
一次函数求最值,常转化为求解不等式ax+b≥0(或≤0), 解答时,注意系数a 的正负,也可以结合函数图象或其单调 性来求最值.
构建一次函数模型的规律方法:
经过最初的锻炼,刘小宁已经能轻松解决
一些简单的问题,得到经理的认可。随着 工作的不断进步,工资奖金的增加,盐小 高宁会采用怎样的方式进行理财投资呢 理财投资可是我们每个人的必修课哦。
建模之旅
刘小宁工作了一段时间后,有了一些积蓄,想进行理财投资,根据长期收益
率市场预测,投资债券等稳健型产品的年收益与投资额成正比,其关系如图1;
投资股票等风险型产品的年收益与投资额的算术平方根成正比,其关系如图2.
(1)帮小宁写出两种产品的年收益f(x)和g(x)
的函数关系式;
(2)其家庭现有20万元资金,全部用于理财投
资,问:怎么分配资金能使投资获得最大年收益
,其最大年收益是多少万元 (图1) (图2)
类型2:二次 函数与幂函数 模型的应用
第二幕:生活小有目标,投资也要做好
( 2 ) 设 投 资 债 券 类 产 品x 万 元 ,
则 股 票 类 投 资 为 ( 2 0 -x) 万 元 , 年 收 益 为V 万
元 ,
依 题 意 得 :y=f(x)+g(20-x),
学生们积极参与,不断补充,帮助刘小宁完成 投资计划。
解 : ( 1 ) 可 设f(x)=k x(x≥0),
所以当t=2, 即 x=16万元时,
收益最大,vmx=3万元
t=√20-x,
则x=20-t ,t∈[0.2 √5],
。
g(x)=k √x(x≥0),
·· ··
则
重
二次函数模型的解析式为g(x)=ax +bx+c(a≠0) 在函数建模中,它占有重
要的地位.在根据实际问题建立函数解析式后,可利用配方法、判别式法、 换元法、函数的单调性等方法来求函数的最值,从而解决实际问题中的最值
问题.也可利用换元最终来求函数的最值.
幂函数模型h(x)=x“在函数建模中,使用频率也比较高,主要可以利用单调
性求出最值。
构建二次函数模型与幂函数模型的规律方法
刘小宁每个月负责交自己家和妈妈家的水费,该市居民自来水收费标准如下:每户每月用水不超过4 吨时,每吨为
1.80元,当用水超过4 吨时,超过部分每吨为3.00元,每月自己家、父母家两户共交水费V 元,已知两户该月用
水量分别为5x,3x.
(1 ) V 关于x 的函数关系式
(2)若两户该月共交水费264元,分别求出甲、乙两户该月的用水量.
小组合作,同学们联手为刘小宁和宁妈排忧解难
类型3:分段
函数模型的
应用
第三幕:生活新手小白遇到水费小麻烦
(1)由题意知,x≥0,令5x=4,得 ;令 则当 时 ,y=(5x+3x)×1.8=14.4x,
时,
时,
(2)由于y=fx)在各段区间上均单增,
当 时 重
当
当 时,令24x-9.6=26.4, 得 x=1.5,
所以刘小宁户用水量为5x=7.5 吨,付费
S =4×1.8+3.5×3=17.70 元
宁妈用水量为3x=4.5 吨,付费S =8.7 元.
=24x-9.6,
即得
1.分段函数的“段”一定要分得合理不重不漏
2.分段函数的定义域为对应每一段自变量取值范围的并集.
3.分段函数的值域求法:逐段求函数值的范围,最后比较再下
结论 .
构建分段函数模型的规律方法
德育之效:立德树人,培养优秀人才
第四幕:依法纳税,履行公民义务
依法纳税是每个公民应尽的义务,个人取得的所得应依照《中华人民共和国个人所得税法》向国
家缴纳个人所得税(简称个税).2019 年1 月1日起,个税税额根据应纳税所得额、税率和速算扣除
数确定,计算公式为个税税额=应纳税所得额×税率-速算扣除数.应纳税所得额的计算公式为应纳税所
得额=综合所得收入额-基本减除费用-专项扣除-专项附加扣除-依法确定的其他扣除.其中,“基本减除
费 用”(免征额)为每年60000元,税率与速算扣除数见表
级 数 全年应纳税所得 额所在区间 税 率 ( % )
速算扣除
数
1 [0.36000] 3
0
2 (36000,144000)| 10
2520
3 [144000,300000] 20
16920
4 [300000.420000] 25
31920
5 (420000.660000) 30
52920
6 (660000,960000) 35
85920
7 (960000,+00) 45
181920
结合3.1.2例8的解析式,应缴纳综合所得个税税额y 关全年综合所得收入额为x(单位:
元)的函数解析式为
(1)如果小王全年的综合所得由189600 元增加到249600元,那么他全年应缴纳多少
综合所得个税
1、理解问题
2、简化假设
3、构建数学(函数)模型
4、求解模型
5、检验模型
6、评价与应用
建模的主要步骤:
课堂小结
1.解有关函数的应用题,首先应考虑选择哪一种函数作为模型,然后
建立其解析式.求解析式时, 一般利用待定系数法,要充分挖掘题目的
隐含条件,充分利用函数图形的直观性.
2 .数学建模的过程图示如下:
实际问题 数学对象 数学模型
推理或
演算
实际问题的解 数学模型的解
解释
评价
数学建模
的过程图示如下:
一次函数
二次函数
幂函数
分段函数
板书设计
函数
数学对象
数学模型
应用
实际问题的解
实际题
数学模型的解
评价 解释
推或
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
