高中数学人教A版必修1幂函数课件(共21张PPT)
文档属性
| 名称 | 高中数学人教A版必修1幂函数课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-13 23:38:47 | ||
图片预览




文档简介
(共21张PPT)
2.3 幂函数
一 、实例探究
1、如果小红购买了每千克1元的水果x千克,那么她需 要付的钱数y是 y=x
2、如果正方形的边长为x, 那么正方形的面积y 为
3、如果正方体的边长为x, 那么正方体的体积y 为
y=x
4、如果正方形场地面积为x, 那么正方形的边长y为
y=x
5、如果小兰在x秒内骑车行进了1km, 那么她骑车的速 度y是 y=x-
下列哪些是幂函数 (2)(5)
0y=0.2*; (2)
(4)y=x*; (5)y=x ;
二 、基础知识讲解
1、幂函数的定义:
y=xa
(3)y=3x ;
(6)y=1
(2)y=x (3)y=x
(5)y=x-
(1)y=x
(4)y=x
1
二 、基础知识讲解
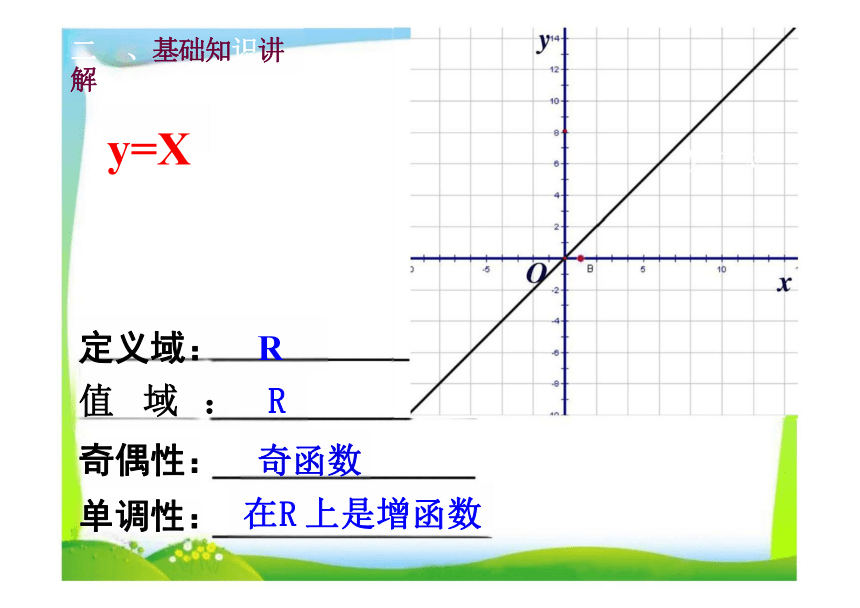
定义域: R
值 域 : R
奇偶性: 奇函数
单调性: 在R 上是增函数
二 、基础知识讲解
y=X
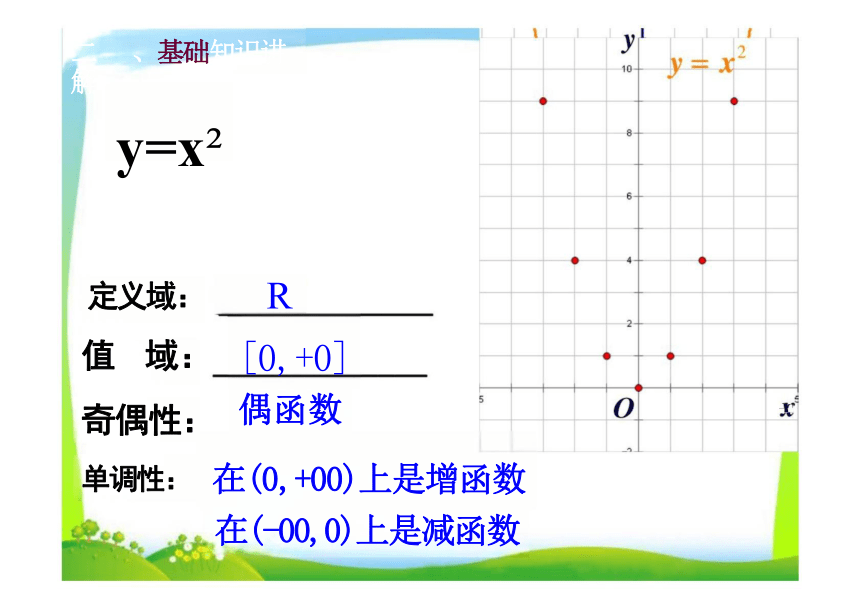
R
[0,+0]
偶函数
在(0,+00)上是增函数
定义域:
值 域: 奇偶性: 单调性:
二 、基础知识讲解
y=x
在(-00,0)上是减函数
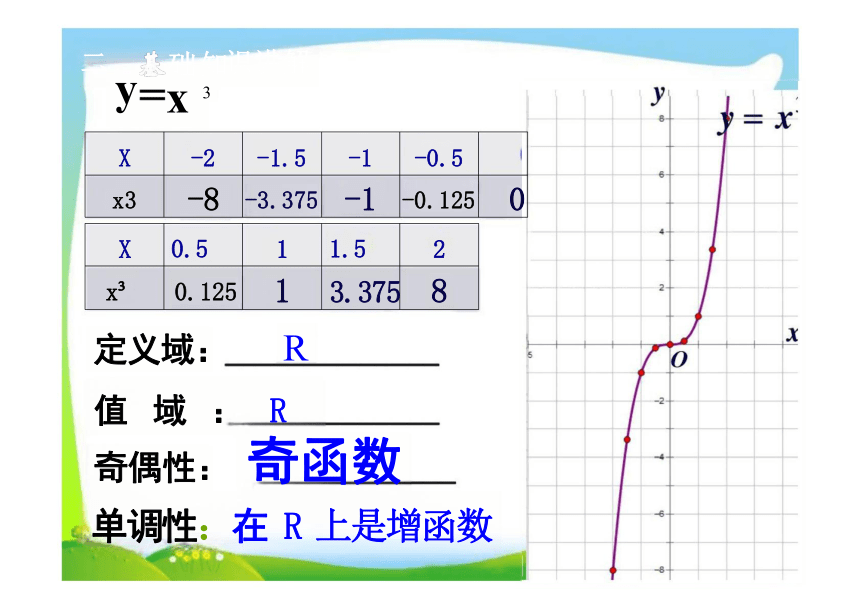
定义域: R
值 域 : R
奇偶性: 奇函数
单调性:在 R 上是增函数
X -2 -1.5 -1 -0.5
x3 -8 -3.375 -1 -0.125
0
X 0.5 1 1.5
2
x 0.125 1 3.375
8
二、y 识讲解
3
知
x
础
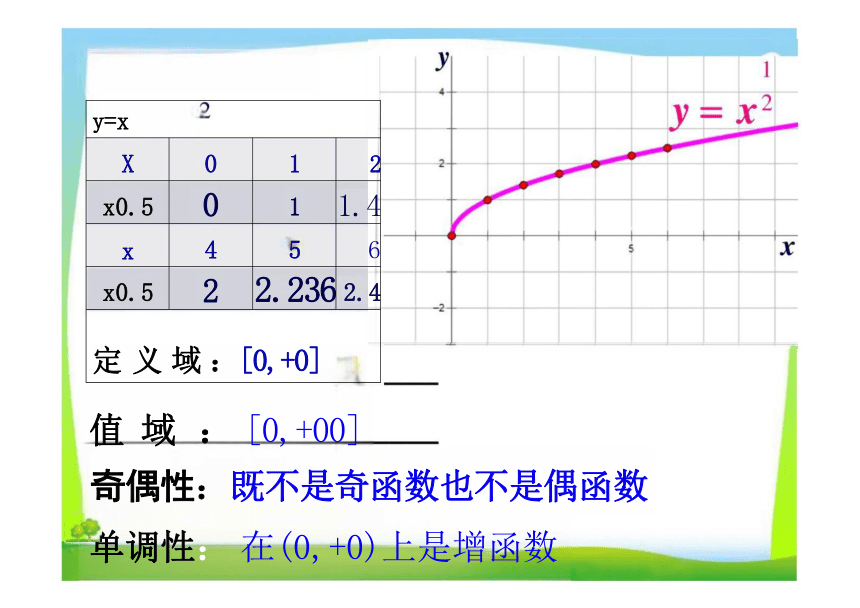
值 域 : [0,+00]
奇偶性:既不是奇函数也不是偶函数
单调性: 在(0,+0)上是增函数
y=x
X 0 1
2
x0.5 0 1
1.4
x 4 5
6
x0.5 2 2.236
2.4
定 义 域 :[0,+0]
二 、基 础知识讲解
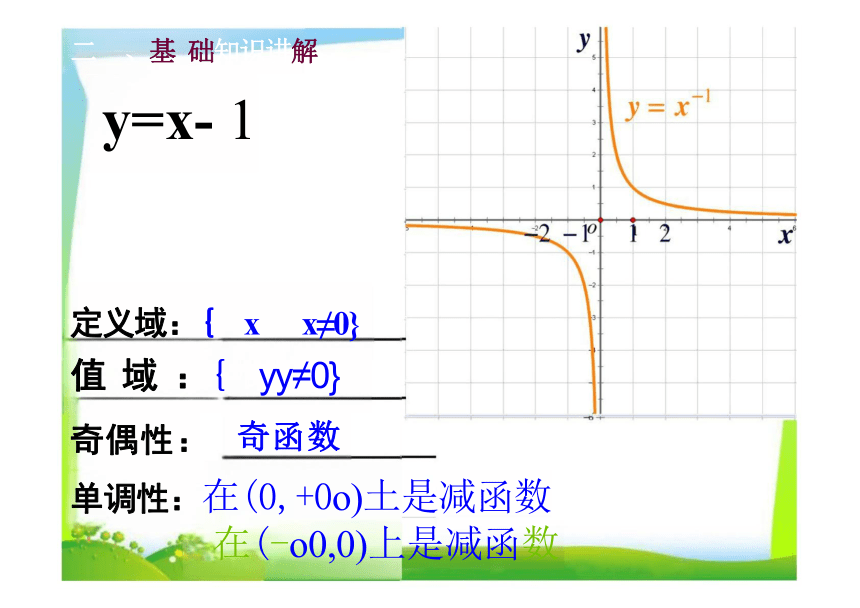
y=x- 1
定义域:{ x x≠0}
值 域 :{ yy≠0}
奇偶性: 奇函数
单调性:在(0,+0o)土是减函数 在(-o0,0)上是减函数
X
3-
-1 0
3-
X
1
几个幂函数的图象和性质
y=x y=x y=x 1 y=x
y=x-1
定义域 R R (0,+o)
{x|x≠0}
值域 (0,+0) R (0,+oo)
{yly≠0}
奇偶性 奇 偶 奇 非奇非偶
奇
单调性 (0, +0o) ( 一 0 , 0)
(0,+o)
( 一 0 , 0)
(1,1)
(0,0)
二 基础知识讲解
规律:
(1)所有的幂函数y=x “均在(0,+0)上有定义, 过公共点(1,1)
(2)当a>0 时,y=x “的图象过原点(0,0) 当α<0 时 ,y=x “的图象不过原点;
(3)当α是奇数时 ,y=x" 是奇函数,
当α是偶数时,y=x “是偶函数;
(4)在区间(0,+0)上,
当α>0 时,函数y=x “是增函数;
当α<0 时 ,y=x" 是减函数,图象与两坐标轴
的正半轴无限接近;
例题
例1 函 数f(x)=(m -m-1)xm +m-3 是幂函数,且当 x∈(0,+00)时 ,f(x) 单调递增,求f(x) 的解析式。
解:Qf(x)=(m -m-1)x m +m-3是幂函数,
∴m -m-1=1
解得m=2 或m=-1,
当m=2 时 ,m +m-3=3, 即f(x)=x ,
满足在(0,+0o)上是增函数;
当m=-1 时 ,m +m-3=-3, 即f(x)=x - ,
在(0,+00)上是减函数,不符合题意;
所 求函数解析式为f(x)=x .
例题
例2、证明幂函数f(x)=√x 在(0,+00)上是增函数。
证明:任取x ,x ∈(0,+00),设 xf(x )-f(x )=√x-√x
Qx ,x ∈[0,+0],且 x∴x-x <0,√x +√x >0,
∴f(x )-f(x )<0,即f(x )f (x )= √x 在[0,+00]上是增函数.
三 、例题分析
例3、用所学的图象和性质,比较下列各组值的大小:
1 1
(1)3.14 与π (2)(-0.38) 与(-0.39)
(3)1.25- 与1.22-
解:(1)幂函数y=x 在区间[0,+0]上是增函数
1
Q3.14<π ∴3.14 <π2
(2)
Q-0.38>-0.39 ∴:(-0.38) >(-0.39)
三 、例题分析
例3、用所学的图象和性质,比较下列各组值的大小:
1 1
(1)3.14 与π (2)(-0.38) 与(-0.39)
(3)1.25- 与1.22-
(3)y=x- 在(0,+0)上减函数
Q1.25>1.22 ∴1.25- <1.22-1
在(-00,+00)上是减函数,<指数函数 Q-0.25>-0.27
变式、已知 ,求m取值范围.
四、练习巩固
P868、 已知函数f(x)=(m +2m) ·xm +m-1, 求m为何值时,f(x) 为
(1)正比例函数;(2)反比例函数;(3)二次函数;(4)幂函数
【解析】(1)若f(x)为正比例函数,
则
(2)若f(x)为反比例函数,
则 →m= 1.
(3)若f(x)为二次函数,
则
(4)若f(x)为幂函数,则m +2m=1,∴m=— 1±√2.
五、 课堂小结
1 、定义:一般地,函数 f(x)=xa 叫做幂函数,其中x 是自变量,α是常数。
2、注意
区分幂函数与指数函数的概念及其表达式
3、幂函数 f(x)=xα的性质:
当α是奇数时 ,y=x “是奇函数;当α是偶数时,y=x “是偶函数; 1.a>0 时,(1)图象都经过点(0,0)和(1,1);
(2)函数在(0,+oo)上是增函数。
2. a<0 时,(1)图象都经过点(1,1);
(2)函数在(0,+o)上是减函数,且向右无限接 近x轴,向上无限接近y轴。
作业
● (1)在同一个坐标系中,画出本节学习的 5个幂函数图象。注意标出关键点和坐标轴。
●(2)
求f(x)=log (x -4x+3
●完成练习册相关内容
令t=x -4x+3=(x-2) -7, 当 x∈(-o0,1)U(3,+00) 时t>0,
∴y=log t, t ∈(0,+0o) , ② 确定内外函数,求中间量范围 ∴当x∈(-0,1) 时,t=x -4x+3 单调递减,此时t ∈(0,+0); 当x∈(3,+0)时,t=x -4x+3 单调递增,此时t∈(0,+00);
而当t∈(0,+o) 时 ,y=log t 单调递增, 内外函数
. 函数f(x)=log (x -4x+3) 在区间(-00,1)上单调递减,
在区间(3,+00)上单调递增.
④”同增异减”下结论
单调性
③分析
解:由题意可得:x -4x+3>0,
∴定义域是(-o,1)U(3,+0)
国数f(x)=log (x -4x+3 前
解得x<1 或x>3,
①求定义域
2.3 幂函数
一 、实例探究
1、如果小红购买了每千克1元的水果x千克,那么她需 要付的钱数y是 y=x
2、如果正方形的边长为x, 那么正方形的面积y 为
3、如果正方体的边长为x, 那么正方体的体积y 为
y=x
4、如果正方形场地面积为x, 那么正方形的边长y为
y=x
5、如果小兰在x秒内骑车行进了1km, 那么她骑车的速 度y是 y=x-
下列哪些是幂函数 (2)(5)
0y=0.2*; (2)
(4)y=x*; (5)y=x ;
二 、基础知识讲解
1、幂函数的定义:
y=xa
(3)y=3x ;
(6)y=1
(2)y=x (3)y=x
(5)y=x-
(1)y=x
(4)y=x
1
二 、基础知识讲解
定义域: R
值 域 : R
奇偶性: 奇函数
单调性: 在R 上是增函数
二 、基础知识讲解
y=X
R
[0,+0]
偶函数
在(0,+00)上是增函数
定义域:
值 域: 奇偶性: 单调性:
二 、基础知识讲解
y=x
在(-00,0)上是减函数
定义域: R
值 域 : R
奇偶性: 奇函数
单调性:在 R 上是增函数
X -2 -1.5 -1 -0.5
x3 -8 -3.375 -1 -0.125
0
X 0.5 1 1.5
2
x 0.125 1 3.375
8
二、y 识讲解
3
知
x
础
值 域 : [0,+00]
奇偶性:既不是奇函数也不是偶函数
单调性: 在(0,+0)上是增函数
y=x
X 0 1
2
x0.5 0 1
1.4
x 4 5
6
x0.5 2 2.236
2.4
定 义 域 :[0,+0]
二 、基 础知识讲解
y=x- 1
定义域:{ x x≠0}
值 域 :{ yy≠0}
奇偶性: 奇函数
单调性:在(0,+0o)土是减函数 在(-o0,0)上是减函数
X
3-
-1 0
3-
X
1
几个幂函数的图象和性质
y=x y=x y=x 1 y=x
y=x-1
定义域 R R (0,+o)
{x|x≠0}
值域 (0,+0) R (0,+oo)
{yly≠0}
奇偶性 奇 偶 奇 非奇非偶
奇
单调性 (0, +0o) ( 一 0 , 0)
(0,+o)
( 一 0 , 0)
(1,1)
(0,0)
二 基础知识讲解
规律:
(1)所有的幂函数y=x “均在(0,+0)上有定义, 过公共点(1,1)
(2)当a>0 时,y=x “的图象过原点(0,0) 当α<0 时 ,y=x “的图象不过原点;
(3)当α是奇数时 ,y=x" 是奇函数,
当α是偶数时,y=x “是偶函数;
(4)在区间(0,+0)上,
当α>0 时,函数y=x “是增函数;
当α<0 时 ,y=x" 是减函数,图象与两坐标轴
的正半轴无限接近;
例题
例1 函 数f(x)=(m -m-1)xm +m-3 是幂函数,且当 x∈(0,+00)时 ,f(x) 单调递增,求f(x) 的解析式。
解:Qf(x)=(m -m-1)x m +m-3是幂函数,
∴m -m-1=1
解得m=2 或m=-1,
当m=2 时 ,m +m-3=3, 即f(x)=x ,
满足在(0,+0o)上是增函数;
当m=-1 时 ,m +m-3=-3, 即f(x)=x - ,
在(0,+00)上是减函数,不符合题意;
所 求函数解析式为f(x)=x .
例题
例2、证明幂函数f(x)=√x 在(0,+00)上是增函数。
证明:任取x ,x ∈(0,+00),设 x
Qx ,x ∈[0,+0],且 x
∴f(x )-f(x )<0,即f(x )
三 、例题分析
例3、用所学的图象和性质,比较下列各组值的大小:
1 1
(1)3.14 与π (2)(-0.38) 与(-0.39)
(3)1.25- 与1.22-
解:(1)幂函数y=x 在区间[0,+0]上是增函数
1
Q3.14<π ∴3.14 <π2
(2)
Q-0.38>-0.39 ∴:(-0.38) >(-0.39)
三 、例题分析
例3、用所学的图象和性质,比较下列各组值的大小:
1 1
(1)3.14 与π (2)(-0.38) 与(-0.39)
(3)1.25- 与1.22-
(3)y=x- 在(0,+0)上减函数
Q1.25>1.22 ∴1.25- <1.22-1
在(-00,+00)上是减函数,<指数函数 Q-0.25>-0.27
变式、已知 ,求m取值范围.
四、练习巩固
P868、 已知函数f(x)=(m +2m) ·xm +m-1, 求m为何值时,f(x) 为
(1)正比例函数;(2)反比例函数;(3)二次函数;(4)幂函数
【解析】(1)若f(x)为正比例函数,
则
(2)若f(x)为反比例函数,
则 →m= 1.
(3)若f(x)为二次函数,
则
(4)若f(x)为幂函数,则m +2m=1,∴m=— 1±√2.
五、 课堂小结
1 、定义:一般地,函数 f(x)=xa 叫做幂函数,其中x 是自变量,α是常数。
2、注意
区分幂函数与指数函数的概念及其表达式
3、幂函数 f(x)=xα的性质:
当α是奇数时 ,y=x “是奇函数;当α是偶数时,y=x “是偶函数; 1.a>0 时,(1)图象都经过点(0,0)和(1,1);
(2)函数在(0,+oo)上是增函数。
2. a<0 时,(1)图象都经过点(1,1);
(2)函数在(0,+o)上是减函数,且向右无限接 近x轴,向上无限接近y轴。
作业
● (1)在同一个坐标系中,画出本节学习的 5个幂函数图象。注意标出关键点和坐标轴。
●(2)
求f(x)=log (x -4x+3
●完成练习册相关内容
令t=x -4x+3=(x-2) -7, 当 x∈(-o0,1)U(3,+00) 时t>0,
∴y=log t, t ∈(0,+0o) , ② 确定内外函数,求中间量范围 ∴当x∈(-0,1) 时,t=x -4x+3 单调递减,此时t ∈(0,+0); 当x∈(3,+0)时,t=x -4x+3 单调递增,此时t∈(0,+00);
而当t∈(0,+o) 时 ,y=log t 单调递增, 内外函数
. 函数f(x)=log (x -4x+3) 在区间(-00,1)上单调递减,
在区间(3,+00)上单调递增.
④”同增异减”下结论
单调性
③分析
解:由题意可得:x -4x+3>0,
∴定义域是(-o,1)U(3,+0)
国数f(x)=log (x -4x+3 前
解得x<1 或x>3,
①求定义域
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
