2024年陕西省西安市雁塔区高新逸翠园中学中考数学十七模试卷(含答案)
文档属性
| 名称 | 2024年陕西省西安市雁塔区高新逸翠园中学中考数学十七模试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 229.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-12 21:35:11 | ||
图片预览




文档简介
2024年陕西省西安市雁塔区高新逸翠园中学中考数学十七模试卷
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
1.我市某天的最高气温是,最低气温是,则这一天的最高气温与最低气温的差为( )
A. B. C. D.
2.既是轴对称图形又是中心对称图形的是( )
A. 菱形 B. 等边三角形 C. 平行四边形 D. 扇形
3.下列计算正确的是( )
A. B. C. D.
4.如图,已知,,,则的值为( )
A.
B.
C.
D.
5.如图,在中,,平分交于点,,交于点,若,则的度数是( )
A.
B.
C.
D.
6.已知一次函数的函数值随的增大而减小,那么下列哪个点一定不在该函数图象上( )
A. B. C. D.
7.如图,内接于,点是的中点,是的直径若,,则的长为( )
A.
B.
C.
D.
8.若二次函数与轴没有交点,则二次函数的图象的顶点在( )
A. 第四象限 B. 第三象限 C. 第二象限 D. 第一象限
二、填空题:本题共5小题,每小题3分,共15分。
9.实数和在数轴上的位置如图所示,则 ______填“”“”或“”
10.正边形的中心角为,则 .
11.年第届杭州亚运会的会徽“潮涌”将自然奇观与人文精
神进行巧妙融合,其中浪潮设计借助了黄金分割比以给人协调的美感
如图,若点可看作是线段的黄金分割点,,
则 ______结果保留根号
12.已知函数与的图象相交于,两点,若,则的值为______.
13.如图,在扇形中,,,点是上一动点,连接,过点作于点,连接当的长度最小时,图中阴影部分的面积为______.
三、计算题:本大题共1小题,共5分。
14.计算:.
四、解答题:本题共12小题,共76分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
解不等式组:.
16.本小题分
解方程:.
17.本小题分
如图,为上一点,已知,求证:.
18.本小题分
已知平行四边形请用尺规作图法,在边上找一点,使得保留作图痕迹,不写作法
19.本小题分
小明要代表区参加市举办的禁毒知识竞赛,共有道题,规定答对一道题得分,答错或不答一道题扣分,只有得分超过分才能获得决赛资格.向小明至少答对多少道题才能获得决赛资格?
20.本小题分
刘老师将个红球和若干个黄球放入一个不透明的口袋中并搅匀,这些球除颜色不同外其余都相同,他让若干学生进行摸球试验,每次摸出一个球,记下颜色后,放回搅匀,经过多次实验发现,从袋中摸出一个球是红球的频率稳定在附近.
估算袋中黄球的个数;
在的条件下,小强同学从中任意摸出一个球,放回并搅匀,再摸一次球,用画树状图或列表的方法计算他两次都摸出黄球的概率.
21.本小题分
如图,小明同学看见斜坡上有一棵小树,他想测量小树的高度,站在坡底处,目光从点出发,以水平视线观察小树底端,即,在阳光照射下,小树的影子顶端与小明的影子顶端在地面的点处重合可视为,,三点在同一直线上小明通过测量估算斜坡的坡度:,,,,,图中所有点均在同一平面内,请你根据题中数据计算小树的高度结果精确到
22.本小题分
沙漏又称“沙钟”,是我国古代一种计量时间的装置它是根据均匀的沙粒从一玻璃球漏到另一个玻璃球的数量来计量时间其中上面玻璃球中沙粒完全流入下面玻璃球后立即将沙漏倒置倒置时间忽略不计,重新进行计时,周而复始某课外数学小组观察发现:该沙漏上面玻璃球沙粒剩余量粒与流入时间秒成一次函数关系不考虑其他因素,当流入时间在第秒时,上面玻璃球剩余沙粒粒,当流入时间在第秒时,上面玻璃球剩余沙粒粒.
求出上面玻璃球沙粒余量粒与流入时间秒之间的函数关系式;
求沙漏恰好完成第一次倒置所需时间.
23.本小题分
年春节假期,西安文旅全面复苏,接待人次、旅游收入双创新高;重点景区人气爆棚,持续高位运行据统计,年月日到月日期间,西安共接待游客约万人次其中著名打卡景区有,:大唐不夜城,:秦始皇帝博物院,:大唐芙蓉园,:华清宫景区,:华山景区,:其他小志为了解哪个景区最受欢迎,随机调查了自己学校的部分同学,并根据调查结果绘制了人数两个完整的统计图.
请你根据统计图中的信息,解决下列问题:
这次调查一共抽取了______名同学;扇形统计图中,旅游地点所对应的扇形圆心角的度数______.
请补全条形统计图.
若小志所在学校共有名学生,请你根据调查结果估计该校最喜爱“大唐不夜城”和“大唐芙蓉园”的学生人数.
24.本小题分
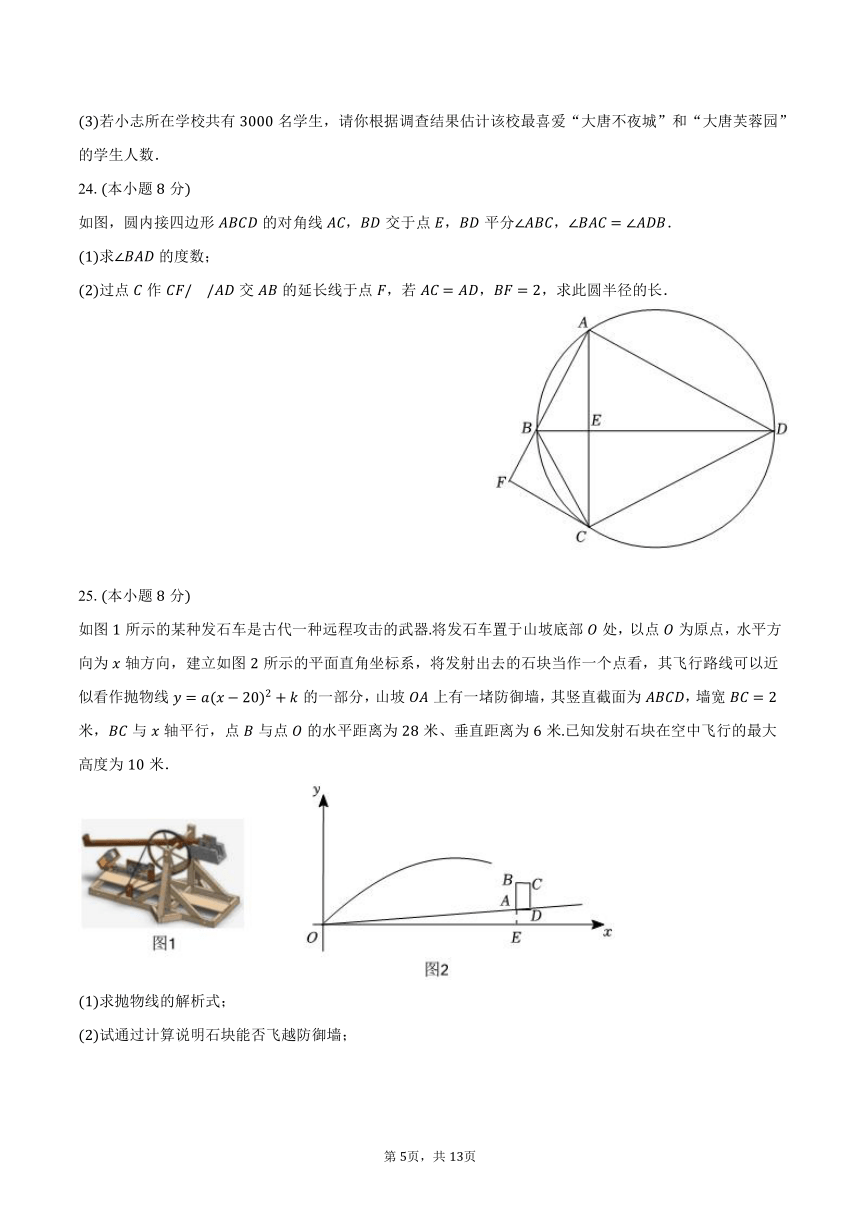
如图,圆内接四边形的对角线,交于点,平分,.
求的度数;
过点作交的延长线于点,若,,求此圆半径的长.
25.本小题分
如图所示的某种发石车是古代一种远程攻击的武器将发石车置于山坡底部处,以点为原点,水平方向为轴方向,建立如图所示的平面直角坐标系,将发射出去的石块当作一个点看,其飞行路线可以近似看作抛物线的一部分,山坡上有一堵防御墙,其竖直截面为,墙宽米,与轴平行,点与点的水平距离为米、垂直距离为米已知发射石块在空中飞行的最大高度为米.
求抛物线的解析式;
试通过计算说明石块能否飞越防御墙;
26.本小题分
“乐思”小组开展探究四点共圆的条件活动时,得到结论:对角互补的四边形的四个顶点共圆,该小组继续利用上述结论进行探究.
问题探究:如图,四边形为矩形,平分,交于点,.
判断、、、四点是否共圆?填“是”或“不是” ______.
______.
问题解决:如图,某公园内有一个五边形人工湖,已知,米,,点是上一点,且,点是直线上一点,夏季来临,为了增加游客的安全性,欲在其中央建造一个以为斜边的等腰直角型救助站,如图所示,已知湖岸米,点是上的中点,是湖岸通向救助站的唯一通道,若修筑通道的造价为每米元,求当造价最低时,四边形的面积为多少?并求出通道的最低造价.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.解:原式
.
15.解:,
解不等式得,,
解不等式得,,
则不等式组的解集为.
16.解:去分母得:,
解得:,
检验:把代入得:,
分式方程的解为.
17.证明:,,
,
,,
≌,
.
18.解:如图,点即为所求;
四边形为平行四边形,
,
,
是的平分线,
,
,
.
19.解:设小明答对道题,则答错或不答道题,
依题意,得:,
解得:.
为正整数,
的最小值为.
答:小明至少答对道题才能获得决赛资格.
20.解:设袋子中黄球有个,
根据从袋中摸出一个红球的概率大约是可得,
解得:,
经检验:时原分式方程的解,
估算袋中黄球的个数为;
画树状图得:
共有种等可能的结果,两次都摸到黄球的有种情况,
两次都摸出黄球的概率为.
21.解:如图,延长交于点,
,,,
四边形为矩形,
,
斜坡的坡度:,即,
,
解得,,
,,
,
∽,
,即,
,
解得,.
所以小树的高度约为.
22.解:设一次函数的解析式.
将和分别代入.得
解得.
.
沙漏恰好完成第一次倒置,
.
即,解得.
沙漏恰好完成第一次倒置的时间是秒.
23.,;
景点人数为名,
名,
答:估计该校最喜爱“大唐不夜城”和“大唐芙蓉园”的学生有名.
24.解:,,
,
,
平分,
,
,
是圆的直径,
;
,
,
,
,
是等边三角形,
,
,
,
,
,
,,
,
,
,,
,
圆的半径长是.
25.解:由题意,发射石块在空中飞行的最大高度为米,
.
石块运行的函数关系式为.
把代入解析式得:,
.
,即.
石块能飞越防御墙,理由如下:
点与点的水平距离为米,且米,
可令代入得:
.
,
石块能飞越防御墙.
26.是;
;
延长,交于点,连接,过点作于点,过点作于点,连接并延长交于点,过点作于点,
,
四边形为矩形,
,米,
,,
,
,
是等腰直角三角形,
,,
,
≌,
,
平分,,
点为中点,,
米,
点在以点为圆心,为半径的上运动,
,
当点与点重合,点与点重合时,最小即为,
在中,,米,
米,
米,
最低造价为:元,
当点与点重合时,如图:
,,,
四边形是矩形,
,
四边形是正方形,
≌,
,
,,
米.
第1页,共1页
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
1.我市某天的最高气温是,最低气温是,则这一天的最高气温与最低气温的差为( )
A. B. C. D.
2.既是轴对称图形又是中心对称图形的是( )
A. 菱形 B. 等边三角形 C. 平行四边形 D. 扇形
3.下列计算正确的是( )
A. B. C. D.
4.如图,已知,,,则的值为( )
A.
B.
C.
D.
5.如图,在中,,平分交于点,,交于点,若,则的度数是( )
A.
B.
C.
D.
6.已知一次函数的函数值随的增大而减小,那么下列哪个点一定不在该函数图象上( )
A. B. C. D.
7.如图,内接于,点是的中点,是的直径若,,则的长为( )
A.
B.
C.
D.
8.若二次函数与轴没有交点,则二次函数的图象的顶点在( )
A. 第四象限 B. 第三象限 C. 第二象限 D. 第一象限
二、填空题:本题共5小题,每小题3分,共15分。
9.实数和在数轴上的位置如图所示,则 ______填“”“”或“”
10.正边形的中心角为,则 .
11.年第届杭州亚运会的会徽“潮涌”将自然奇观与人文精
神进行巧妙融合,其中浪潮设计借助了黄金分割比以给人协调的美感
如图,若点可看作是线段的黄金分割点,,
则 ______结果保留根号
12.已知函数与的图象相交于,两点,若,则的值为______.
13.如图,在扇形中,,,点是上一动点,连接,过点作于点,连接当的长度最小时,图中阴影部分的面积为______.
三、计算题:本大题共1小题,共5分。
14.计算:.
四、解答题:本题共12小题,共76分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
解不等式组:.
16.本小题分
解方程:.
17.本小题分
如图,为上一点,已知,求证:.
18.本小题分
已知平行四边形请用尺规作图法,在边上找一点,使得保留作图痕迹,不写作法
19.本小题分
小明要代表区参加市举办的禁毒知识竞赛,共有道题,规定答对一道题得分,答错或不答一道题扣分,只有得分超过分才能获得决赛资格.向小明至少答对多少道题才能获得决赛资格?
20.本小题分
刘老师将个红球和若干个黄球放入一个不透明的口袋中并搅匀,这些球除颜色不同外其余都相同,他让若干学生进行摸球试验,每次摸出一个球,记下颜色后,放回搅匀,经过多次实验发现,从袋中摸出一个球是红球的频率稳定在附近.
估算袋中黄球的个数;
在的条件下,小强同学从中任意摸出一个球,放回并搅匀,再摸一次球,用画树状图或列表的方法计算他两次都摸出黄球的概率.
21.本小题分
如图,小明同学看见斜坡上有一棵小树,他想测量小树的高度,站在坡底处,目光从点出发,以水平视线观察小树底端,即,在阳光照射下,小树的影子顶端与小明的影子顶端在地面的点处重合可视为,,三点在同一直线上小明通过测量估算斜坡的坡度:,,,,,图中所有点均在同一平面内,请你根据题中数据计算小树的高度结果精确到
22.本小题分
沙漏又称“沙钟”,是我国古代一种计量时间的装置它是根据均匀的沙粒从一玻璃球漏到另一个玻璃球的数量来计量时间其中上面玻璃球中沙粒完全流入下面玻璃球后立即将沙漏倒置倒置时间忽略不计,重新进行计时,周而复始某课外数学小组观察发现:该沙漏上面玻璃球沙粒剩余量粒与流入时间秒成一次函数关系不考虑其他因素,当流入时间在第秒时,上面玻璃球剩余沙粒粒,当流入时间在第秒时,上面玻璃球剩余沙粒粒.
求出上面玻璃球沙粒余量粒与流入时间秒之间的函数关系式;
求沙漏恰好完成第一次倒置所需时间.
23.本小题分
年春节假期,西安文旅全面复苏,接待人次、旅游收入双创新高;重点景区人气爆棚,持续高位运行据统计,年月日到月日期间,西安共接待游客约万人次其中著名打卡景区有,:大唐不夜城,:秦始皇帝博物院,:大唐芙蓉园,:华清宫景区,:华山景区,:其他小志为了解哪个景区最受欢迎,随机调查了自己学校的部分同学,并根据调查结果绘制了人数两个完整的统计图.
请你根据统计图中的信息,解决下列问题:
这次调查一共抽取了______名同学;扇形统计图中,旅游地点所对应的扇形圆心角的度数______.
请补全条形统计图.
若小志所在学校共有名学生,请你根据调查结果估计该校最喜爱“大唐不夜城”和“大唐芙蓉园”的学生人数.
24.本小题分
如图,圆内接四边形的对角线,交于点,平分,.
求的度数;
过点作交的延长线于点,若,,求此圆半径的长.
25.本小题分
如图所示的某种发石车是古代一种远程攻击的武器将发石车置于山坡底部处,以点为原点,水平方向为轴方向,建立如图所示的平面直角坐标系,将发射出去的石块当作一个点看,其飞行路线可以近似看作抛物线的一部分,山坡上有一堵防御墙,其竖直截面为,墙宽米,与轴平行,点与点的水平距离为米、垂直距离为米已知发射石块在空中飞行的最大高度为米.
求抛物线的解析式;
试通过计算说明石块能否飞越防御墙;
26.本小题分
“乐思”小组开展探究四点共圆的条件活动时,得到结论:对角互补的四边形的四个顶点共圆,该小组继续利用上述结论进行探究.
问题探究:如图,四边形为矩形,平分,交于点,.
判断、、、四点是否共圆?填“是”或“不是” ______.
______.
问题解决:如图,某公园内有一个五边形人工湖,已知,米,,点是上一点,且,点是直线上一点,夏季来临,为了增加游客的安全性,欲在其中央建造一个以为斜边的等腰直角型救助站,如图所示,已知湖岸米,点是上的中点,是湖岸通向救助站的唯一通道,若修筑通道的造价为每米元,求当造价最低时,四边形的面积为多少?并求出通道的最低造价.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.解:原式
.
15.解:,
解不等式得,,
解不等式得,,
则不等式组的解集为.
16.解:去分母得:,
解得:,
检验:把代入得:,
分式方程的解为.
17.证明:,,
,
,,
≌,
.
18.解:如图,点即为所求;
四边形为平行四边形,
,
,
是的平分线,
,
,
.
19.解:设小明答对道题,则答错或不答道题,
依题意,得:,
解得:.
为正整数,
的最小值为.
答:小明至少答对道题才能获得决赛资格.
20.解:设袋子中黄球有个,
根据从袋中摸出一个红球的概率大约是可得,
解得:,
经检验:时原分式方程的解,
估算袋中黄球的个数为;
画树状图得:
共有种等可能的结果,两次都摸到黄球的有种情况,
两次都摸出黄球的概率为.
21.解:如图,延长交于点,
,,,
四边形为矩形,
,
斜坡的坡度:,即,
,
解得,,
,,
,
∽,
,即,
,
解得,.
所以小树的高度约为.
22.解:设一次函数的解析式.
将和分别代入.得
解得.
.
沙漏恰好完成第一次倒置,
.
即,解得.
沙漏恰好完成第一次倒置的时间是秒.
23.,;
景点人数为名,
名,
答:估计该校最喜爱“大唐不夜城”和“大唐芙蓉园”的学生有名.
24.解:,,
,
,
平分,
,
,
是圆的直径,
;
,
,
,
,
是等边三角形,
,
,
,
,
,
,,
,
,
,,
,
圆的半径长是.
25.解:由题意,发射石块在空中飞行的最大高度为米,
.
石块运行的函数关系式为.
把代入解析式得:,
.
,即.
石块能飞越防御墙,理由如下:
点与点的水平距离为米,且米,
可令代入得:
.
,
石块能飞越防御墙.
26.是;
;
延长,交于点,连接,过点作于点,过点作于点,连接并延长交于点,过点作于点,
,
四边形为矩形,
,米,
,,
,
,
是等腰直角三角形,
,,
,
≌,
,
平分,,
点为中点,,
米,
点在以点为圆心,为半径的上运动,
,
当点与点重合,点与点重合时,最小即为,
在中,,米,
米,
米,
最低造价为:元,
当点与点重合时,如图:
,,,
四边形是矩形,
,
四边形是正方形,
≌,
,
,,
米.
第1页,共1页
同课章节目录
