2024年江苏省南京市联合体中考数学模拟试卷(二)(含答案)
文档属性
| 名称 | 2024年江苏省南京市联合体中考数学模拟试卷(二)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 120.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-12 21:09:28 | ||
图片预览



文档简介
2024年江苏省南京市联合体中考数学模拟试卷(二)
一、选择题:本题共6小题,每小题2分,共12分。在每小题给出的选项中,只有一项是符合题目要求的。
1.的平方根是( )
A. B. C. D.
2.下列运算正确的是
A. B. C. D.
3.的取值范围是( )
A. B. C. D.
4.如图,菱形的边长是,是的中点,且,则菱形的面积为( )
A.
B.
C.
D.
5.实数,满足,,下列结论:,,,其中所有正确结论的序号是( )
A. B. C. D.
6.如图,在中,,为的切线,为切点,,则和的面积之比为( )
A. B. C. D.
二、填空题:本题共10小题,每小题2分,共20分。
7.的倒数是______;的相反数是______.
8.若式子在实数范围内有意义,则的取值范围是______.
9.计算的结果是______.
10.方程的根是______.
11.正方形内接于,是的中点,连接、,则 ______
12.如图,将绕点顺时针旋转到的位置连接,若,则 ______
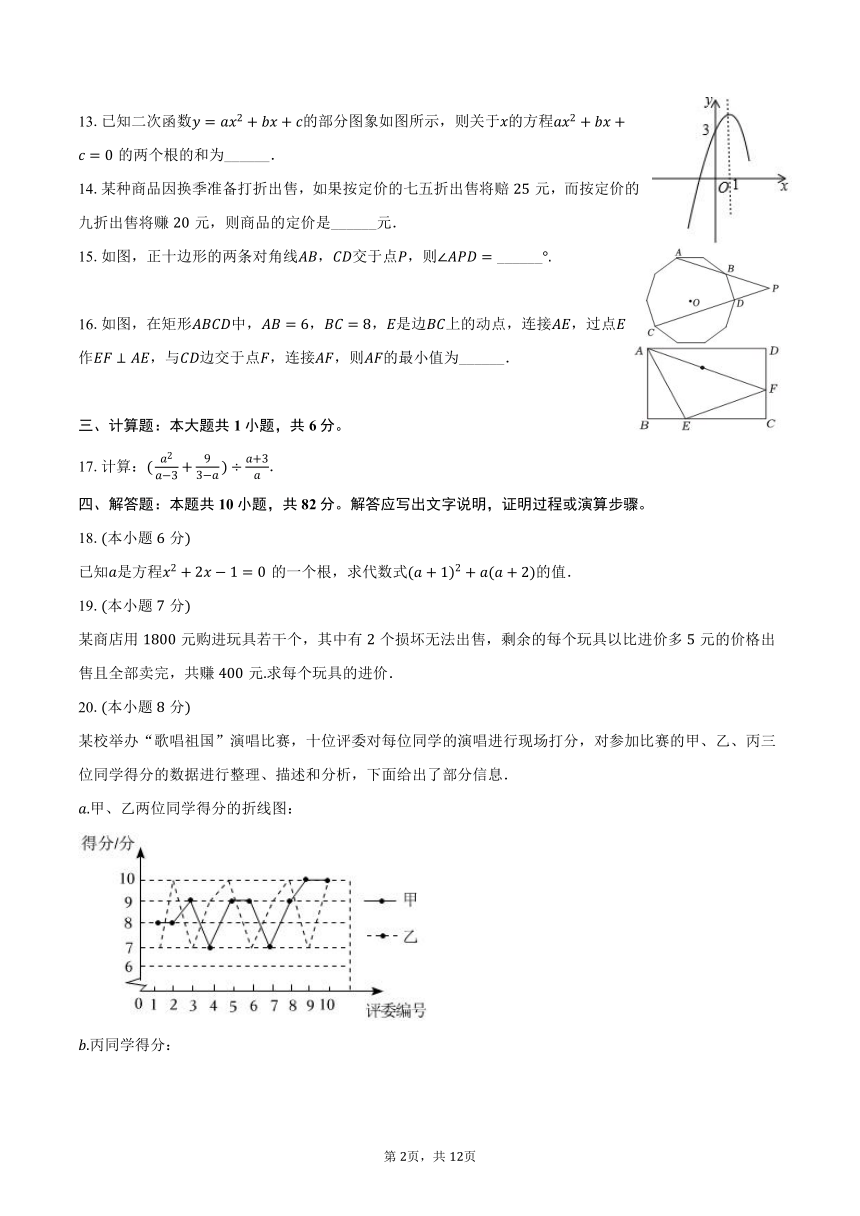
13.已知二次函数的部分图象如图所示,则关于的方程的两个根的和为______.
14.某种商品因换季准备打折出售,如果按定价的七五折出售将赔元,而按定价的九折出售将赚元,则商品的定价是______元.
15.如图,正十边形的两条对角线,交于点,则 ______
16.如图,在矩形中,,,是边上的动点,连接,过点作,与边交于点,连接,则的最小值为______.
三、计算题:本大题共1小题,共6分。
17.计算:.
四、解答题:本题共10小题,共82分。解答应写出文字说明,证明过程或演算步骤。
18.本小题分
已知是方程的一个根,求代数式的值.
19.本小题分
某商店用元购进玩具若干个,其中有个损坏无法出售,剩余的每个玩具以比进价多元的价格出售且全部卖完,共赚元求每个玩具的进价.
20.本小题分
某校举办“歌唱祖国”演唱比赛,十位评委对每位同学的演唱进行现场打分,对参加比赛的甲、乙、丙三位同学得分的数据进行整理、描述和分析,下面给出了部分信息.
甲、乙两位同学得分的折线图:
丙同学得分:
,,,,,,,,,
甲、乙、丙三位同学得分的平均数:
同学 甲 乙 丙
平均数
根据以上信息,回答下列问题:
表中的值为______;丙同学得分的众数是______;
在参加比赛的同学中,如果某同学得分的个数据的方差越小,则认为评委对该同学演唱的评价越一致据此推断:甲、乙两位同学中,评委对______的评价更一致填“甲”或“乙”;
如果每位同学的最后得分为去掉十位评委打分中的一个最高分和一个最低分后的平均分,最后得分越高,则认为该同学表现越优秀据此推断:在甲、乙、丙三位同学中,表现最优秀的是______填“甲”或“乙”或“丙”.
21.本小题分
某班举行元旦晚会,表演形式有舞蹈、话剧、唱歌和朗诵种,甲、乙两名同学分别从种类型中随机挑选两种参加.
求甲选择舞蹈、话剧两种类型的概率;
甲、乙两人选择的两种节目类型都不相同的概率是______.
22.本小题分
如图,在平行四边形中,过点作于点,点在边上,,连接,.
求证:四边形是矩形;
若平分,,,求四边形的面积.
23.本小题分
,两地相距,一辆快车和一辆慢车分别从,两地同时出发相向而行,相遇后两车继续行驶快车到达地后立即按原路原速返回,慢车到达地后停止快、慢两车离地的距离,单位:与出发时间单位:之间的函数关系如图所示.
补全与之间的函数图象;
若慢车的速度为.
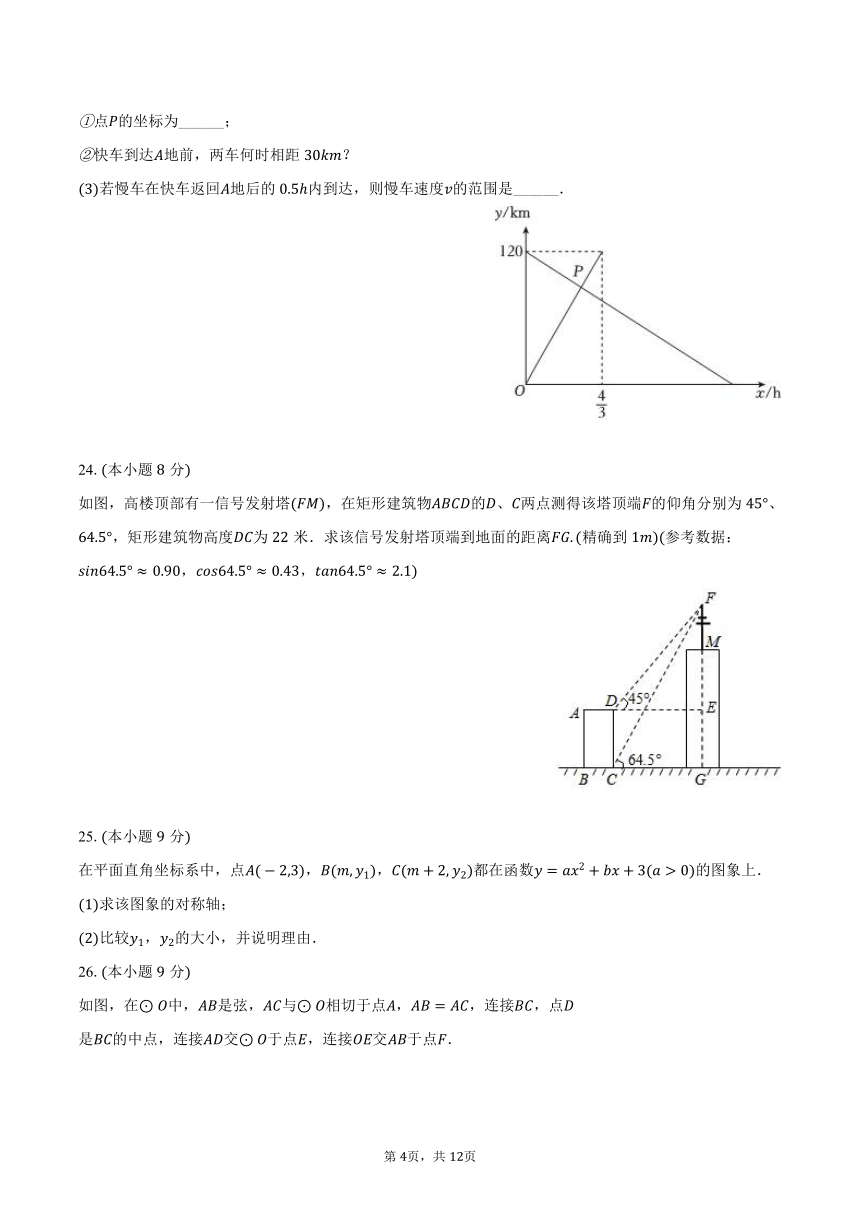
点的坐标为______;
快车到达地前,两车何时相距?
若慢车在快车返回地后的内到达,则慢车速度的范围是______.
24.本小题分
如图,高楼顶部有一信号发射塔,在矩形建筑物的、两点测得该塔顶端的仰角分别为、,矩形建筑物高度为米.求该信号发射塔顶端到地面的距离精确到参考数据:,,
25.本小题分
在平面直角坐标系中,点,,都在函数的图象上.
求该图象的对称轴;
比较,的大小,并说明理由.
26.本小题分
如图,在中,是弦,与相切于点,,连接,点
是的中点,连接交于点,连接交于点.
求证:;
若,,求的半径.
27.本小题分
问题背景
如图,在中,,,,点、分别是边、上的动点,过点做的垂线,垂足为,连结,设,两点之间的距离为,、两点之间的距离为
初步运用
当时,______;
思维探究
若与全等,则______;
思维拓展
如图,以,为邻边作 ,当时,是否存在,使得 的顶点恰好落在的边上?若存在,请求出的值,若不存在,请说明理由.
参考答案
1.
2.
3.
4.
5.
6.
7.;
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.解:原式
.
18.解:
,
是方程的一个根,
,
,
则原式.
19.解:设每个玩具的进价是元,
根据题意得:,
解得:,不符合题意,舍去,
经检验,是原方程的解,且符合题意,
答:每个玩具的进价是元.
20.;;
甲;
丙.
21.将“舞蹈、话剧、唱歌、朗诵”种表演形式分别记为,,,.
列表如下:
共有种等可能的结果,其中甲选择舞蹈、话剧两种类型的结果有:,,共种,
甲选择舞蹈、话剧两种类型的概率为.
.
22.证明:四边形是平行四边形,
,,
又,
,
四边形是平行四边形,
,
,
四边形是矩形.
解:平分,,
,,
,
,
,
,,
,
矩形的面积是:.
23.
【解析】解:快车到达地后立即按原路原速返回,
快车返回地时,;
补全与之间的函数图象如下:
;
根据题意得,
当时,,
两车相距,
,
解得或;
当时,,
两车相距,
,
解得或;
综上所述,或或或时,两车相距;
.
24.解:设,由题意得米,米.
在中,,
米,
在中,,
米,
,
,
解得,
米.
答:该信号发射塔顶端到地面的距离约为米.
25.解:由题意,令,,
抛物线过点.
点在抛物线上,
点和点是抛物线上的对称点.
对称轴为直线.
由题意,对称轴为直线,
.
.
,
当时,;
当时,;
当时,.
26.证明:连接、,如图所示.
与相切于点,
.
设,则.
,
,
.
,是的中点,
,
,
.
又,
.
解:,
可设,.
,是的中点,
,,
.
,
,解得:,
,.
,
.
,,
∽,
,即,
.
设的半径为,则,,
,
,即,
解得:,
的半径为.
27. ;
或 ;
如图,落在上,过作于点,
易知四边形是矩形,则,
在中,、、,
则;
如图,落在上,过作于点,同上,
在中,,
,由三垂直模型知∽,
,
.
第1页,共1页
一、选择题:本题共6小题,每小题2分,共12分。在每小题给出的选项中,只有一项是符合题目要求的。
1.的平方根是( )
A. B. C. D.
2.下列运算正确的是
A. B. C. D.
3.的取值范围是( )
A. B. C. D.
4.如图,菱形的边长是,是的中点,且,则菱形的面积为( )
A.
B.
C.
D.
5.实数,满足,,下列结论:,,,其中所有正确结论的序号是( )
A. B. C. D.
6.如图,在中,,为的切线,为切点,,则和的面积之比为( )
A. B. C. D.
二、填空题:本题共10小题,每小题2分,共20分。
7.的倒数是______;的相反数是______.
8.若式子在实数范围内有意义,则的取值范围是______.
9.计算的结果是______.
10.方程的根是______.
11.正方形内接于,是的中点,连接、,则 ______
12.如图,将绕点顺时针旋转到的位置连接,若,则 ______
13.已知二次函数的部分图象如图所示,则关于的方程的两个根的和为______.
14.某种商品因换季准备打折出售,如果按定价的七五折出售将赔元,而按定价的九折出售将赚元,则商品的定价是______元.
15.如图,正十边形的两条对角线,交于点,则 ______
16.如图,在矩形中,,,是边上的动点,连接,过点作,与边交于点,连接,则的最小值为______.
三、计算题:本大题共1小题,共6分。
17.计算:.
四、解答题:本题共10小题,共82分。解答应写出文字说明,证明过程或演算步骤。
18.本小题分
已知是方程的一个根,求代数式的值.
19.本小题分
某商店用元购进玩具若干个,其中有个损坏无法出售,剩余的每个玩具以比进价多元的价格出售且全部卖完,共赚元求每个玩具的进价.
20.本小题分
某校举办“歌唱祖国”演唱比赛,十位评委对每位同学的演唱进行现场打分,对参加比赛的甲、乙、丙三位同学得分的数据进行整理、描述和分析,下面给出了部分信息.
甲、乙两位同学得分的折线图:
丙同学得分:
,,,,,,,,,
甲、乙、丙三位同学得分的平均数:
同学 甲 乙 丙
平均数
根据以上信息,回答下列问题:
表中的值为______;丙同学得分的众数是______;
在参加比赛的同学中,如果某同学得分的个数据的方差越小,则认为评委对该同学演唱的评价越一致据此推断:甲、乙两位同学中,评委对______的评价更一致填“甲”或“乙”;
如果每位同学的最后得分为去掉十位评委打分中的一个最高分和一个最低分后的平均分,最后得分越高,则认为该同学表现越优秀据此推断:在甲、乙、丙三位同学中,表现最优秀的是______填“甲”或“乙”或“丙”.
21.本小题分
某班举行元旦晚会,表演形式有舞蹈、话剧、唱歌和朗诵种,甲、乙两名同学分别从种类型中随机挑选两种参加.
求甲选择舞蹈、话剧两种类型的概率;
甲、乙两人选择的两种节目类型都不相同的概率是______.
22.本小题分
如图,在平行四边形中,过点作于点,点在边上,,连接,.
求证:四边形是矩形;
若平分,,,求四边形的面积.
23.本小题分
,两地相距,一辆快车和一辆慢车分别从,两地同时出发相向而行,相遇后两车继续行驶快车到达地后立即按原路原速返回,慢车到达地后停止快、慢两车离地的距离,单位:与出发时间单位:之间的函数关系如图所示.
补全与之间的函数图象;
若慢车的速度为.
点的坐标为______;
快车到达地前,两车何时相距?
若慢车在快车返回地后的内到达,则慢车速度的范围是______.
24.本小题分
如图,高楼顶部有一信号发射塔,在矩形建筑物的、两点测得该塔顶端的仰角分别为、,矩形建筑物高度为米.求该信号发射塔顶端到地面的距离精确到参考数据:,,
25.本小题分
在平面直角坐标系中,点,,都在函数的图象上.
求该图象的对称轴;
比较,的大小,并说明理由.
26.本小题分
如图,在中,是弦,与相切于点,,连接,点
是的中点,连接交于点,连接交于点.
求证:;
若,,求的半径.
27.本小题分
问题背景
如图,在中,,,,点、分别是边、上的动点,过点做的垂线,垂足为,连结,设,两点之间的距离为,、两点之间的距离为
初步运用
当时,______;
思维探究
若与全等,则______;
思维拓展
如图,以,为邻边作 ,当时,是否存在,使得 的顶点恰好落在的边上?若存在,请求出的值,若不存在,请说明理由.
参考答案
1.
2.
3.
4.
5.
6.
7.;
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.解:原式
.
18.解:
,
是方程的一个根,
,
,
则原式.
19.解:设每个玩具的进价是元,
根据题意得:,
解得:,不符合题意,舍去,
经检验,是原方程的解,且符合题意,
答:每个玩具的进价是元.
20.;;
甲;
丙.
21.将“舞蹈、话剧、唱歌、朗诵”种表演形式分别记为,,,.
列表如下:
共有种等可能的结果,其中甲选择舞蹈、话剧两种类型的结果有:,,共种,
甲选择舞蹈、话剧两种类型的概率为.
.
22.证明:四边形是平行四边形,
,,
又,
,
四边形是平行四边形,
,
,
四边形是矩形.
解:平分,,
,,
,
,
,
,,
,
矩形的面积是:.
23.
【解析】解:快车到达地后立即按原路原速返回,
快车返回地时,;
补全与之间的函数图象如下:
;
根据题意得,
当时,,
两车相距,
,
解得或;
当时,,
两车相距,
,
解得或;
综上所述,或或或时,两车相距;
.
24.解:设,由题意得米,米.
在中,,
米,
在中,,
米,
,
,
解得,
米.
答:该信号发射塔顶端到地面的距离约为米.
25.解:由题意,令,,
抛物线过点.
点在抛物线上,
点和点是抛物线上的对称点.
对称轴为直线.
由题意,对称轴为直线,
.
.
,
当时,;
当时,;
当时,.
26.证明:连接、,如图所示.
与相切于点,
.
设,则.
,
,
.
,是的中点,
,
,
.
又,
.
解:,
可设,.
,是的中点,
,,
.
,
,解得:,
,.
,
.
,,
∽,
,即,
.
设的半径为,则,,
,
,即,
解得:,
的半径为.
27. ;
或 ;
如图,落在上,过作于点,
易知四边形是矩形,则,
在中,、、,
则;
如图,落在上,过作于点,同上,
在中,,
,由三垂直模型知∽,
,
.
第1页,共1页
同课章节目录
