《多边形的面积》单元作业设计人教版五年级上册数学
文档属性
| 名称 | 《多边形的面积》单元作业设计人教版五年级上册数学 |
|
|
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-12 12:16:35 | ||
图片预览




文档简介
作业设计
(
《多边形的面积》选自人教版数学五年级上册第六单元,它属于“图形与几何”中的“测量”部分。本单元的主要内容有:平行四边形的面积、三角形的面积、梯形的面积、组合图形的面积和方格图中不规则图形的面积估算。通过本单元的学习,一方面让学生运用转化的思想推导出面积计算公式,积累数学活动经验。另一方面在自主探索组合图形面积等活动中发展空间观念。同时,本单元的内容也是进一步学习圆面积和立体图形表面积的基础。《义务教育数学课程标准(2022年版)》指出“学生对身边与数学有关的事物有好奇心”“不同的人在数学上有不同发展”,基于此,在进行作业设计时,依据学生学情,从教学经验出发,设计分层作业主要分为基础性、提升性、发展性和实践性作业,让作业既有趣又有挑战性,让学生在作业中巩固新知,引发思考,从而培养学生思维,提升学习能力,使学生成为学习的主导者。
)一、单元作业概况
二、案例征文
(
《义务教育数学课程标准(2022年版)》对本单元学习的要求有以下两点:
1.在课程内容的第二学段中提出了探索并掌握三角形、平行四边形和梯形的面积公式,并能解决简单的实际问题。
2.会用方格纸估计不规则图形的面积。
)(一)学科核心素养细化
(二)单元大概念架构
(
单元学习目标
) (
本单元主要教学内容是引导学生运用转化的方法,在动手操作的基础上掌握三角形、平行四边形和梯形的面积计算公式,会正确地应用计算公式求图形的面积,能解决生活中有关面积的实际问题。故提炼本单元大概念为:“运用转化,度量计算"。
) (
本单元的学习,主要是学生通过观察、实验、猜想、验证等活动,利用转化思想推导出平行四边形、三角形、梯形面积公式,发展合情“推理能力”,促进学生“空间观念”的进一步发展、在推导过程中利用学具、绘图等工具感受“几何直观”,
总结字母公式体会“符号意识”的作用,在计算不规则图形的面积时,渗透估测意识、策略,发展学生“量感”,而组合图形面积的计算,让学生了解解决问题方法
的多样性,增强数学“应用意识”和“创新意识”。
) (
1.让学生利用转化思想,通过动手操作、实验观察等方法,探索并掌握平行四边形、三角形和梯形的面积公式。
2.让学生会用面积公式计算平行四边形、三角形和梯形的面积,并能解决生活中一些简单的实际问题。
3.通过学生对组合图形的面积的计算,培养学生空间观念及解决问题的能力。
4.让学生会用方格纸估计不规则图形的面积,培养估算意识。
)
(
提升性目标:
1.加强图形之间的沟通和转化,能灵活的运用公式。
2.理解图形各部分之间的关系,解决生活中的实际问题。
3.关注推理能力,会恰当的运用面积计算公式的逆运算,让学生正确理解底、高和面积、及周长之间的关系,并能理解图形各部分之间的联系,培养对图形的分析能力,发展几何直观。
4.通过图形分割和转化方法,培养学生解决问题的多样化,提高运用知识解决实际问题的能力。
5.培养学生的观察力和想象力,引导学生养成先分析再解题的好习惯。感受数学与生活之间的密切联系,体会学数学、用数学的乐趣。
) (
基础性目标:
1.会用面积公式计算长方形、正方形、平行四边形、三角形和梯形的面积。
2.用添补法,割补法等计算组合图形的面积。
3.会用方格纸估算不规则图形的面积。
) (
作业设计目标
)
(
发展性目标:
1.加深对图形特征的认识,建立图形敏感,感受图形之间的关系,体会图形面积公式之间的联系。
2.通过数格子、估一估等活动,能灵活运用各种策略与方法估计不规则图形的面积,感受估算思想。
3.寻找图形之间的联系,培养学生“空间观念”、“推理能力”、“几何直观”“模型思想”,发展核心素养。
)
(
实践性目标:
1.让学生通过测量、收集数据、计算、绘制图画等活动,加深对相关面积计算的理解,提高综合应用数学知识和方法解决实际问题的能力。
2.在综合与实践活动中使学生体验学习数学的乐趣,激发学习的兴趣和探求知识的欲望。
)
(三)整体教学流程透视
(
多边形的面积
平行四边形的面积
三角形的面积
梯形的面积
组合图形的面积
解决问题(不规则图形的面积)
例1
例2
例3
例4
例5
)
(
多边形面积的计算是在学生掌握了这些图形的特征以及长方形和正方形面积计算公式的基础上进行教学。教材以长方形面积计算公式为基础,以图形内在联系为线索,以未知转化为已知的基本方法开展学习。
)
(
平行四边形面积
长方形面积
三角形面积
梯形面积
转化
转化
)
(
转化
)
(
在动手操作、合作学习中,经历自主探索的全过程。由于不规则图形的面积无法用面积公式直接计算出来,需要借助方格图大致地衡量其面积,培养学生的估算意识和估算策略。
)
(
01
)(四)作业具体内容设计
基础篇
一、我会填:
正方形的面积=( )×( ), 用字母表示为S=( )。
长方形的面积=( )×( ), 用字母表示为S=( )。
平行四边形的面积=( )×( ), 用字母表示为S=( )。
三角形的面积=( )×( )÷( ),用字母表示为S=( )。
梯形的面积=( + )×( )÷( ),
用字母表示为S=( )。
(
【设计意图】
掌握正方形、长方形、平行四边形、三角形和梯形的面积计算公式及字母表示形式。
)
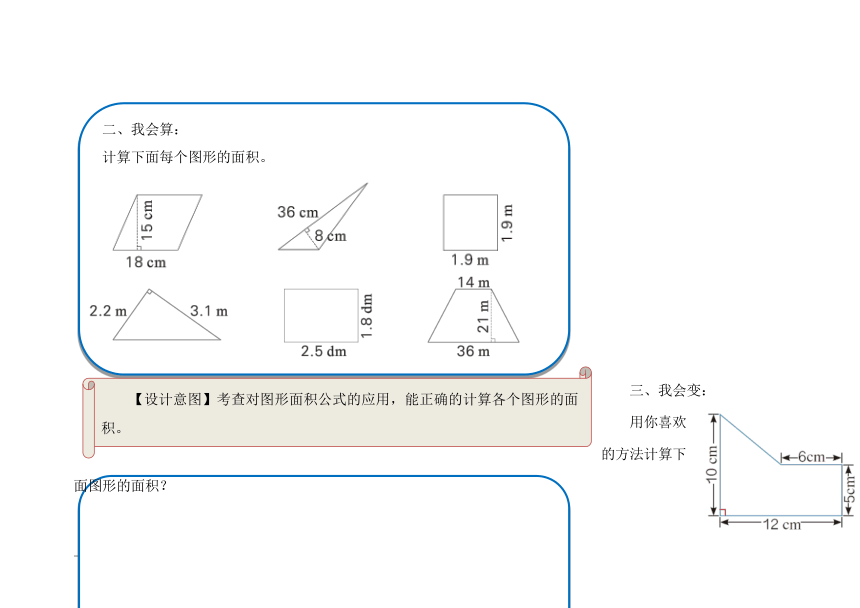
二、我会算:
计算下面每个图形的面积。
(
【设计意图】
考查对图形面积公式的应用,能正确的计算各个图形的面积。
)
三、我会变:
用你喜欢的方法计算下面图形的面积?
(
【设计意图】考查寻找对应数据来求面积的能力,并会用添补法或割补法等,解决组合图形的面积,激发学生多样化的思维。
)
四、我会数:
1.下面三个图形中,( )的面积最大。(不满 1 格的按半格计算)
(
【设计意图】
不规则图形面积的估算是学生学习的难点,通过这样的方式,让学生在活动中不断积累活动经验,掌握估算的方法的同时培养学生细致认真的态度。
)
2.为进一步做好垃圾分类工作,分类垃圾桶上都有类别图示,如下图,
是可回收物中可乐罐类别,请你估一估它在方格图中所占的面积大约是( )平方厘米。(每个小格表示1平方厘米)
(
【设计意图】考查不规则图形面积的估算,以当下倡导的“垃圾分类”为背景,在落实知识发展空间观念的同时,体现育人功能。
)
提升篇
一、我会判:对的打“√”,错的打“×”。
1.一个平行四边形的底是5厘米,高是4分米,
它的面积是20厘米。( )
2.两个等底等高的三角形,面积相等,形状也一定相同。( )
3.在平行四边形中作一个最大的三角形,这个三角形的面积
一定是平行四边形面积的一半。( )
4.求组合图形的面积就是求几个简单图形的面积和。( )
5.两个梯形的上底和下底的和相等,高也相等,它们一定能拼成一个平行四边形。( )
6.估算的面积比实际面积大。( )
(
【设计意图】关注知识的内化和迁移,让学生正确理解底、高和面积之间的关系,并引导学生养成先分析再解题的好习惯。
)
二、我会选:
把正确答案的序号填在括号里。
1.一个三角形和一个平行四边形的面积相等,底也相等。三角形的高是6米,平行四边形的高是( )。
3米 6米 12米
2.把木条做成长方形框架拉成平行四边形,下面说法正确的是( )。
A.周长不变,面积变了 B.周长和面积都不变
C.周长和面积都变了 D.周长变了,面积不变
3.一个平行四边形的两条邻边分别长9厘米和5厘米,其中一条边上的高
是7厘米,则这个平行四边形的面积是( )平方厘米。
A.35 B. 43 C.45 D.63
4.下图平行线中三个图形的面积相比较,( )。
平行四边形面积大 三角形面积大 梯形面积大 一样大
5.如图等腰梯形中,三角形甲与三角形乙的面积的大小关系是( )。
A.甲大于乙
B.甲小于乙
C.甲等于乙
(
【设计意图】关注推理能力,会恰当的运用面积计算公式的逆运算,让学生正确理解底、高和面积,及周长之间的关系,并能理解图形各部分之间的联系。在提高学生观察能力的同时,培养对图形的分析能力,发展几何直观。
)
三、我会用:
1.在一块梯形的地中间有一个长方形的游泳池,其余的地方是草地。
草地的面积是多少平方米?
(
【设计意图】将多边形面积的计算植入生活载体中,激发学生的解题兴趣,一定程度上培养学生丰富的想象力和应用意识,这样的综合练习让学生在解决实际问题中提升应用能力。
)
2.下图中正方形的周长是 32 cm。平行四边形的面积是多少
(
【设计意图】利用等积变形求图形面积。
)
3.草地中间为2米宽的小路,求草地的面积?(单位:米)
(
【设计意图】这种题是学生作业中错误率比较高的,通过平移或转化,培养学生多种策略,运用知识解决实际问题的能力。
)
4.靠墙边围成一个花坛,围花坛的篱笆长 46 m,求这个花坛的面积。
(
【设计意图】培养学生的观察力和想象力,并引导学生养成先分析再解题的好习惯。
)
发展篇
1.这个有一副七巧板拼成的正方形,边长为12cm,
你能求出每个图形的面积吗?
第一级:算出图形①的面积
第二级:算出图形②的面积
第三级:算出图形③的面积
(
【设计意图】关注推理能力,在提高学生观察能力的同时,培养对图形的分析能力,发展几何直观。
)
2.在下面格子图中,分别画一个平行四边形、一个三角形和一个梯形,
使它们的面积都与图中长方形的面积相等。
(
【设计意图】此题根据这些图形的面积公式确定有关边(底、高)的长度。意在考查它们之间既有联系又有区别,这样为学生的可持续发展奠定了很好的基础。
)
3.如下图,小芮家附近有一个世纪公园和中央公园。
(1)世纪公园和中央公园相比,哪个公园的面积大?
(2)与中央公园面积相等的还有哪些区域?请你在图中用 标出来。
(
【设计意图】此题根据这些图形的面积公式确定有关边(底、高)的长度。意在考查它们之间既有联系又有区别,这样为学生的可持续发展奠定了很好的基础。
)
4.采集一片树叶,在方格纸上描出它的轮廓线,再估计它的面积。
五年级上数学《不规则图形面积》学习单 在方格纸上描出秋天的一小片树叶,再用数方格的方法来估一估它的面积(每个小方格是1平方厘米) 我采集的树叶,整格( ),半格( ) 大约( )平方厘米。
(
【设计意图】学生通过动手描一描的制作过程感受制作的快乐,同时培养细致认真的做事态度。然后在估一估的过程中体会不规则图形面积的估算和多边形面积计算的差异。在动手操作的过程中加深对面积计算的理解。
)
(
04
) 实践篇
1.图1是我校美景中的一角——“耕读园”
图2是“耕读园”的轮廓图
你能利用本单元的知识计算出“耕读园”的面吗?
图1
图2
“耕读园面积”学习单
同学们,你知道我们学校的耕读园面积是多少吗?
分组合作,先了解我校耕读园的平面图形是什么图形的组合,
再制定一个测量和统计我校耕读园面积的方案。
我们的方案:
1.小组成员分工:
测量记录:
2.具体实施和计算方法:
3.耕读园面积计算:
(
【设计意图】“耕读园面积”是一次综合与实践活动,主要引导学生围绕需要解决的问题,开展查找资料、测量计算、数据整理和分析讨论等活动,在活动中加深对相关面积计算的理解,提高综合应用数学知识和方法解决实际问题的能力,增强数学应用意识,培养动手实践能力。
)
2.同学们,通过“多边形的面积”单元的学习,我们知道了平行四边形、
三角形、梯形以及组合图形、不规则图形的面积计算方法。你能试着量一量,画一画,估一估、算一算,“以我家的面积”为主题开展面积知识的小研究吗?期待你的精彩作品。
(
【设计意图】在这次实践作业中,围绕需要解决的问题积极开展查找资料、测量计算、数据整理和分析讨论等活动,在活动中加深了对相关面积计算方法的理解,提高综合应用数学知识和方法解决实际问题的能力,增强数学应用意识,培养动手实践能力。
)
。
(五)作业质量效果评估
作业评价量表
评级指标 等级 备注
A B C
答题的准确性 A等,答案正确、过程正确。 B等,答案正确、过程有问题 C等,答案不正确,有过程不完整;答案不准确,过程错误、或无过程。
答题的规范性 A等,答案正确、过程正确。 B等,过程不够规范、完整,答案正确。 C等,过程不规范或无过程,答案错误。
答题的创新性 A等,解法有新意和独到之处,答案正确。 B等,解法思路有创新,答案不完整或错误。 C等,常规解法,思路不清楚,过程复杂或无过程。
综合评价等级 AAA、AAB综合评价为A等;ABB、BBB、AAC综合评价为B等;其余情况综合评价为C等。
(
整体学生觉得基础篇的作业没有难度,都是面积公式的巩固与简单的运用。但是提升篇、发展篇与实践篇要进行深度思考,因为设计的知识点是整个单元,需要学生把学过的第五单元知识在脑海里进行思考,然后筛选,选择对应的知识进行分析,最后解决问题,所以对于部分学困生来说有点难度。提升篇我会选的第1题,运用到面积计算公式的逆运算,这需要对底、高、面积及周长之
间的关系熟练掌握;提升篇我会用的第3题,这种题是学生作业中错误率比较
) (
1.基础性作业难度较低,第 1、2、3题需要 20 分钟,第 4 题需要 5 分钟。
2.提升性作业难度适中,第 1、2 题需要 10 分钟,第 3 题需要 15分钟。
3.发展性作业难度适中,第 1、2、3题需要 20分钟,第 4题需要 15分钟。
4.实践性作业难度较大,第1题需要25 分钟,第2题需要40分钟。
)
(
高的,通过平移或转化,培养学生多种策略,提高运用知识解决实际问题的能力,并养成先分析再解题的好习惯。发展篇的第4题,学生做题兴趣很高并能熟练画出树叶的轮廓图进行估算,在估一估的过程中体会不规则图形面积的估算和多边形面积计算的差异。实践篇的第2题,在活动中加深了对相关面积计算方法的理解,提高综合应用数学知识和方法解决实际问题的能力,但是个别学生动手操作能力不强,测量不精确。以后的作业设计中,部分的题型难度还要降低成浅显易懂型,要让这部分孩子会做,做对。这样孩子们才能找到学习的成就感。
)
(
1.关注个性差异,响应“双减”政策,落实课程理念。既注重学生基础知识和基本技能的获得,又关注学生的个性发展,作业避免了以往的“一刀切”,把关注点落实到每位学生的个性差异上,设计了分层作业,让学生在自己原有能力的基础上再发力。
2.作业设计更加注重数学与生活的联系,让学生感受到生活中处处有数学,体会数学魅力,提高学习数学兴趣。
3.作业设计更加偏向拓展性、实践性,让学生在动手动脑中,思维向纵深发展,为学生由知识到能力转化提供契机。
)三、作业案例 (
- 1 -
)
(
- 22 -
)
(
《多边形的面积》选自人教版数学五年级上册第六单元,它属于“图形与几何”中的“测量”部分。本单元的主要内容有:平行四边形的面积、三角形的面积、梯形的面积、组合图形的面积和方格图中不规则图形的面积估算。通过本单元的学习,一方面让学生运用转化的思想推导出面积计算公式,积累数学活动经验。另一方面在自主探索组合图形面积等活动中发展空间观念。同时,本单元的内容也是进一步学习圆面积和立体图形表面积的基础。《义务教育数学课程标准(2022年版)》指出“学生对身边与数学有关的事物有好奇心”“不同的人在数学上有不同发展”,基于此,在进行作业设计时,依据学生学情,从教学经验出发,设计分层作业主要分为基础性、提升性、发展性和实践性作业,让作业既有趣又有挑战性,让学生在作业中巩固新知,引发思考,从而培养学生思维,提升学习能力,使学生成为学习的主导者。
)一、单元作业概况
二、案例征文
(
《义务教育数学课程标准(2022年版)》对本单元学习的要求有以下两点:
1.在课程内容的第二学段中提出了探索并掌握三角形、平行四边形和梯形的面积公式,并能解决简单的实际问题。
2.会用方格纸估计不规则图形的面积。
)(一)学科核心素养细化
(二)单元大概念架构
(
单元学习目标
) (
本单元主要教学内容是引导学生运用转化的方法,在动手操作的基础上掌握三角形、平行四边形和梯形的面积计算公式,会正确地应用计算公式求图形的面积,能解决生活中有关面积的实际问题。故提炼本单元大概念为:“运用转化,度量计算"。
) (
本单元的学习,主要是学生通过观察、实验、猜想、验证等活动,利用转化思想推导出平行四边形、三角形、梯形面积公式,发展合情“推理能力”,促进学生“空间观念”的进一步发展、在推导过程中利用学具、绘图等工具感受“几何直观”,
总结字母公式体会“符号意识”的作用,在计算不规则图形的面积时,渗透估测意识、策略,发展学生“量感”,而组合图形面积的计算,让学生了解解决问题方法
的多样性,增强数学“应用意识”和“创新意识”。
) (
1.让学生利用转化思想,通过动手操作、实验观察等方法,探索并掌握平行四边形、三角形和梯形的面积公式。
2.让学生会用面积公式计算平行四边形、三角形和梯形的面积,并能解决生活中一些简单的实际问题。
3.通过学生对组合图形的面积的计算,培养学生空间观念及解决问题的能力。
4.让学生会用方格纸估计不规则图形的面积,培养估算意识。
)
(
提升性目标:
1.加强图形之间的沟通和转化,能灵活的运用公式。
2.理解图形各部分之间的关系,解决生活中的实际问题。
3.关注推理能力,会恰当的运用面积计算公式的逆运算,让学生正确理解底、高和面积、及周长之间的关系,并能理解图形各部分之间的联系,培养对图形的分析能力,发展几何直观。
4.通过图形分割和转化方法,培养学生解决问题的多样化,提高运用知识解决实际问题的能力。
5.培养学生的观察力和想象力,引导学生养成先分析再解题的好习惯。感受数学与生活之间的密切联系,体会学数学、用数学的乐趣。
) (
基础性目标:
1.会用面积公式计算长方形、正方形、平行四边形、三角形和梯形的面积。
2.用添补法,割补法等计算组合图形的面积。
3.会用方格纸估算不规则图形的面积。
) (
作业设计目标
)
(
发展性目标:
1.加深对图形特征的认识,建立图形敏感,感受图形之间的关系,体会图形面积公式之间的联系。
2.通过数格子、估一估等活动,能灵活运用各种策略与方法估计不规则图形的面积,感受估算思想。
3.寻找图形之间的联系,培养学生“空间观念”、“推理能力”、“几何直观”“模型思想”,发展核心素养。
)
(
实践性目标:
1.让学生通过测量、收集数据、计算、绘制图画等活动,加深对相关面积计算的理解,提高综合应用数学知识和方法解决实际问题的能力。
2.在综合与实践活动中使学生体验学习数学的乐趣,激发学习的兴趣和探求知识的欲望。
)
(三)整体教学流程透视
(
多边形的面积
平行四边形的面积
三角形的面积
梯形的面积
组合图形的面积
解决问题(不规则图形的面积)
例1
例2
例3
例4
例5
)
(
多边形面积的计算是在学生掌握了这些图形的特征以及长方形和正方形面积计算公式的基础上进行教学。教材以长方形面积计算公式为基础,以图形内在联系为线索,以未知转化为已知的基本方法开展学习。
)
(
平行四边形面积
长方形面积
三角形面积
梯形面积
转化
转化
)
(
转化
)
(
在动手操作、合作学习中,经历自主探索的全过程。由于不规则图形的面积无法用面积公式直接计算出来,需要借助方格图大致地衡量其面积,培养学生的估算意识和估算策略。
)
(
01
)(四)作业具体内容设计
基础篇
一、我会填:
正方形的面积=( )×( ), 用字母表示为S=( )。
长方形的面积=( )×( ), 用字母表示为S=( )。
平行四边形的面积=( )×( ), 用字母表示为S=( )。
三角形的面积=( )×( )÷( ),用字母表示为S=( )。
梯形的面积=( + )×( )÷( ),
用字母表示为S=( )。
(
【设计意图】
掌握正方形、长方形、平行四边形、三角形和梯形的面积计算公式及字母表示形式。
)
二、我会算:
计算下面每个图形的面积。
(
【设计意图】
考查对图形面积公式的应用,能正确的计算各个图形的面积。
)
三、我会变:
用你喜欢的方法计算下面图形的面积?
(
【设计意图】考查寻找对应数据来求面积的能力,并会用添补法或割补法等,解决组合图形的面积,激发学生多样化的思维。
)
四、我会数:
1.下面三个图形中,( )的面积最大。(不满 1 格的按半格计算)
(
【设计意图】
不规则图形面积的估算是学生学习的难点,通过这样的方式,让学生在活动中不断积累活动经验,掌握估算的方法的同时培养学生细致认真的态度。
)
2.为进一步做好垃圾分类工作,分类垃圾桶上都有类别图示,如下图,
是可回收物中可乐罐类别,请你估一估它在方格图中所占的面积大约是( )平方厘米。(每个小格表示1平方厘米)
(
【设计意图】考查不规则图形面积的估算,以当下倡导的“垃圾分类”为背景,在落实知识发展空间观念的同时,体现育人功能。
)
提升篇
一、我会判:对的打“√”,错的打“×”。
1.一个平行四边形的底是5厘米,高是4分米,
它的面积是20厘米。( )
2.两个等底等高的三角形,面积相等,形状也一定相同。( )
3.在平行四边形中作一个最大的三角形,这个三角形的面积
一定是平行四边形面积的一半。( )
4.求组合图形的面积就是求几个简单图形的面积和。( )
5.两个梯形的上底和下底的和相等,高也相等,它们一定能拼成一个平行四边形。( )
6.估算的面积比实际面积大。( )
(
【设计意图】关注知识的内化和迁移,让学生正确理解底、高和面积之间的关系,并引导学生养成先分析再解题的好习惯。
)
二、我会选:
把正确答案的序号填在括号里。
1.一个三角形和一个平行四边形的面积相等,底也相等。三角形的高是6米,平行四边形的高是( )。
3米 6米 12米
2.把木条做成长方形框架拉成平行四边形,下面说法正确的是( )。
A.周长不变,面积变了 B.周长和面积都不变
C.周长和面积都变了 D.周长变了,面积不变
3.一个平行四边形的两条邻边分别长9厘米和5厘米,其中一条边上的高
是7厘米,则这个平行四边形的面积是( )平方厘米。
A.35 B. 43 C.45 D.63
4.下图平行线中三个图形的面积相比较,( )。
平行四边形面积大 三角形面积大 梯形面积大 一样大
5.如图等腰梯形中,三角形甲与三角形乙的面积的大小关系是( )。
A.甲大于乙
B.甲小于乙
C.甲等于乙
(
【设计意图】关注推理能力,会恰当的运用面积计算公式的逆运算,让学生正确理解底、高和面积,及周长之间的关系,并能理解图形各部分之间的联系。在提高学生观察能力的同时,培养对图形的分析能力,发展几何直观。
)
三、我会用:
1.在一块梯形的地中间有一个长方形的游泳池,其余的地方是草地。
草地的面积是多少平方米?
(
【设计意图】将多边形面积的计算植入生活载体中,激发学生的解题兴趣,一定程度上培养学生丰富的想象力和应用意识,这样的综合练习让学生在解决实际问题中提升应用能力。
)
2.下图中正方形的周长是 32 cm。平行四边形的面积是多少
(
【设计意图】利用等积变形求图形面积。
)
3.草地中间为2米宽的小路,求草地的面积?(单位:米)
(
【设计意图】这种题是学生作业中错误率比较高的,通过平移或转化,培养学生多种策略,运用知识解决实际问题的能力。
)
4.靠墙边围成一个花坛,围花坛的篱笆长 46 m,求这个花坛的面积。
(
【设计意图】培养学生的观察力和想象力,并引导学生养成先分析再解题的好习惯。
)
发展篇
1.这个有一副七巧板拼成的正方形,边长为12cm,
你能求出每个图形的面积吗?
第一级:算出图形①的面积
第二级:算出图形②的面积
第三级:算出图形③的面积
(
【设计意图】关注推理能力,在提高学生观察能力的同时,培养对图形的分析能力,发展几何直观。
)
2.在下面格子图中,分别画一个平行四边形、一个三角形和一个梯形,
使它们的面积都与图中长方形的面积相等。
(
【设计意图】此题根据这些图形的面积公式确定有关边(底、高)的长度。意在考查它们之间既有联系又有区别,这样为学生的可持续发展奠定了很好的基础。
)
3.如下图,小芮家附近有一个世纪公园和中央公园。
(1)世纪公园和中央公园相比,哪个公园的面积大?
(2)与中央公园面积相等的还有哪些区域?请你在图中用 标出来。
(
【设计意图】此题根据这些图形的面积公式确定有关边(底、高)的长度。意在考查它们之间既有联系又有区别,这样为学生的可持续发展奠定了很好的基础。
)
4.采集一片树叶,在方格纸上描出它的轮廓线,再估计它的面积。
五年级上数学《不规则图形面积》学习单 在方格纸上描出秋天的一小片树叶,再用数方格的方法来估一估它的面积(每个小方格是1平方厘米) 我采集的树叶,整格( ),半格( ) 大约( )平方厘米。
(
【设计意图】学生通过动手描一描的制作过程感受制作的快乐,同时培养细致认真的做事态度。然后在估一估的过程中体会不规则图形面积的估算和多边形面积计算的差异。在动手操作的过程中加深对面积计算的理解。
)
(
04
) 实践篇
1.图1是我校美景中的一角——“耕读园”
图2是“耕读园”的轮廓图
你能利用本单元的知识计算出“耕读园”的面吗?
图1
图2
“耕读园面积”学习单
同学们,你知道我们学校的耕读园面积是多少吗?
分组合作,先了解我校耕读园的平面图形是什么图形的组合,
再制定一个测量和统计我校耕读园面积的方案。
我们的方案:
1.小组成员分工:
测量记录:
2.具体实施和计算方法:
3.耕读园面积计算:
(
【设计意图】“耕读园面积”是一次综合与实践活动,主要引导学生围绕需要解决的问题,开展查找资料、测量计算、数据整理和分析讨论等活动,在活动中加深对相关面积计算的理解,提高综合应用数学知识和方法解决实际问题的能力,增强数学应用意识,培养动手实践能力。
)
2.同学们,通过“多边形的面积”单元的学习,我们知道了平行四边形、
三角形、梯形以及组合图形、不规则图形的面积计算方法。你能试着量一量,画一画,估一估、算一算,“以我家的面积”为主题开展面积知识的小研究吗?期待你的精彩作品。
(
【设计意图】在这次实践作业中,围绕需要解决的问题积极开展查找资料、测量计算、数据整理和分析讨论等活动,在活动中加深了对相关面积计算方法的理解,提高综合应用数学知识和方法解决实际问题的能力,增强数学应用意识,培养动手实践能力。
)
。
(五)作业质量效果评估
作业评价量表
评级指标 等级 备注
A B C
答题的准确性 A等,答案正确、过程正确。 B等,答案正确、过程有问题 C等,答案不正确,有过程不完整;答案不准确,过程错误、或无过程。
答题的规范性 A等,答案正确、过程正确。 B等,过程不够规范、完整,答案正确。 C等,过程不规范或无过程,答案错误。
答题的创新性 A等,解法有新意和独到之处,答案正确。 B等,解法思路有创新,答案不完整或错误。 C等,常规解法,思路不清楚,过程复杂或无过程。
综合评价等级 AAA、AAB综合评价为A等;ABB、BBB、AAC综合评价为B等;其余情况综合评价为C等。
(
整体学生觉得基础篇的作业没有难度,都是面积公式的巩固与简单的运用。但是提升篇、发展篇与实践篇要进行深度思考,因为设计的知识点是整个单元,需要学生把学过的第五单元知识在脑海里进行思考,然后筛选,选择对应的知识进行分析,最后解决问题,所以对于部分学困生来说有点难度。提升篇我会选的第1题,运用到面积计算公式的逆运算,这需要对底、高、面积及周长之
间的关系熟练掌握;提升篇我会用的第3题,这种题是学生作业中错误率比较
) (
1.基础性作业难度较低,第 1、2、3题需要 20 分钟,第 4 题需要 5 分钟。
2.提升性作业难度适中,第 1、2 题需要 10 分钟,第 3 题需要 15分钟。
3.发展性作业难度适中,第 1、2、3题需要 20分钟,第 4题需要 15分钟。
4.实践性作业难度较大,第1题需要25 分钟,第2题需要40分钟。
)
(
高的,通过平移或转化,培养学生多种策略,提高运用知识解决实际问题的能力,并养成先分析再解题的好习惯。发展篇的第4题,学生做题兴趣很高并能熟练画出树叶的轮廓图进行估算,在估一估的过程中体会不规则图形面积的估算和多边形面积计算的差异。实践篇的第2题,在活动中加深了对相关面积计算方法的理解,提高综合应用数学知识和方法解决实际问题的能力,但是个别学生动手操作能力不强,测量不精确。以后的作业设计中,部分的题型难度还要降低成浅显易懂型,要让这部分孩子会做,做对。这样孩子们才能找到学习的成就感。
)
(
1.关注个性差异,响应“双减”政策,落实课程理念。既注重学生基础知识和基本技能的获得,又关注学生的个性发展,作业避免了以往的“一刀切”,把关注点落实到每位学生的个性差异上,设计了分层作业,让学生在自己原有能力的基础上再发力。
2.作业设计更加注重数学与生活的联系,让学生感受到生活中处处有数学,体会数学魅力,提高学习数学兴趣。
3.作业设计更加偏向拓展性、实践性,让学生在动手动脑中,思维向纵深发展,为学生由知识到能力转化提供契机。
)三、作业案例 (
- 1 -
)
(
- 22 -
)
