【湘教版数学八年级上册同步练习】 5.2二次根式的乘法和除法(含答案)
文档属性
| 名称 | 【湘教版数学八年级上册同步练习】 5.2二次根式的乘法和除法(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-12 17:58:23 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【湘教版数学八年级上册同步练习】
5.2二次根式的乘法和除法
一、单选题
1.墨迹覆盖了等式“”中的运算符号,则覆盖的是( )
A.+ B.- C.× D.÷
2.计算×的结果为( )
A. B.2 C. D.6
3. × =( )
A.2 B.4 C.2+ D.2
4.下列各式中,与 的积为有理数的是( )
A. B. C. D.
5.已知 ,则 的关系是( )
A. B. C. D.
二、填空题
6. 化简: .
7.计算: .
8.化简:(7-5 )2000·(-7-5 )2001= .
9.计算的正确结果是 .
10.计算的结果为 ,这个数落在了数轴上的 段.
11.计算 .
三、计算题
12.化简,求值:(),其中.
13.阅读下列材料,然后回答问题:
在进行二次根式运算时,我们有时会碰上如 、 这样的式子,其实我们还可以将其进一步化简:
;
.
以上这种化简的步骤叫做分母有理化.
还可以用以下方法化简:
.
(1)请用两种方法化简 ;
(2)化简: .
14.阅读下列材料,然后回答问题:
在进行类似于二次根式 的运算时,通常有如下两种方法将其进一步化简:
方法一:
方法二:
(1)请用两种不同的方法化简: ;
(2)化简: .
四、解答题
15.类比和转化是数学中解决新的问题时最常用的数学思想方法.
【学习新知,类比求解】解方程:.
解:去根号,两边同时平方得一元一次方程______,解这个方程,得______.经检验,______是原方程的解.
【学会转化,解决问题】运用上面的方法解下列方程:
(1);
(2).
五、综合题
16.综合题
(1)试比较 与 的大小;
(2)你能比较 与 的大小吗?其中k为正整数.
17.我们知道,若两个有理数的积是1,则称这两个有理数互为倒数.同样的当两个实数 与 的积是1时,我们仍然称这两个实数互为倒数.
(1)判断 与 是否互为倒数,并说明理由;
(2)若实数 是 的倒数,求x和y之间的关系.
18.已知x=2﹣ ,y=2+ ,求代数式的值:
(1)x2+2xy+y2;
(2)x2﹣y2.
六、实践探究题
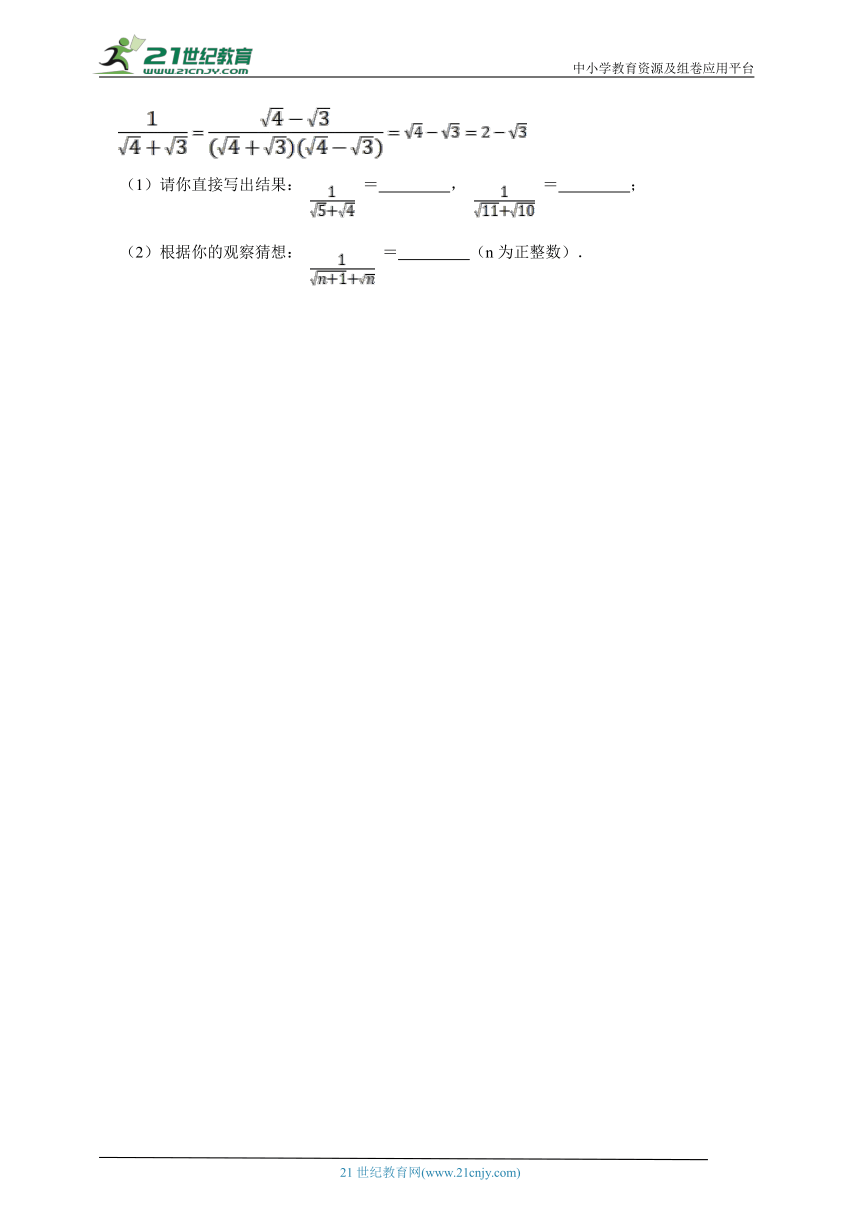
19.先观察下列的等式,再回答问题:
(1)请你直接写出结果: = , = ;
(2)根据你的观察猜想: = (n为正整数).
答案解析部分
1.【答案】D
【知识点】二次根式的乘除法
2.【答案】A
【知识点】二次根式的乘除法
3.【答案】A
【知识点】二次根式的乘除法
4.【答案】D
【知识点】平方差公式及应用;二次根式的乘除法
5.【答案】D
【知识点】分母有理化
6.【答案】##
【知识点】分母有理化
7.【答案】6
【知识点】二次根式的乘除法
8.【答案】-7-5
【知识点】二次根式的乘除法
9.【答案】
【知识点】二次根式的乘除法
10.【答案】;④
【知识点】无理数在数轴上表示;二次根式的乘除法
11.【答案】5
【知识点】二次根式的乘除法
12.【答案】
【知识点】分式的化简求值;分母有理化
13.【答案】(1)解:原式=
(2)解:原式= ;(2)
= =
=
=
【知识点】分母有理化
14.【答案】(1)解:方法一:
方法二:
(2)解:原式=
【知识点】分母有理化;探索数与式的规律
15.【答案】学习新知,类比求解:,,
(1),(2)
【知识点】完全平方公式及运用;二次根式的乘除法
16.【答案】(1)解: ,
,
故 <
(2)解: ,
,
故 <
【知识点】二次根式的性质与化简;二次根式的乘除法
17.【答案】(1)解:因为(4+ )(4- )=16-2=14 1,所以4+ 与4- 不互为倒数
(2)解:因为( + )( - )=x-y,所以当x-y=1时,此两数互为倒数
【知识点】有理数的倒数;平方差公式及应用;二次根式的乘除法
18.【答案】(1)解:x2+2xy+y2
=(x+y)2
=[(2﹣ )+(2+ )]2
=42
=16;
(2)解:x2﹣y2=(x+y)(x﹣y)
=(2﹣ +2+ )(2﹣ ﹣2﹣ )
=4×(﹣2 )
=﹣8 .
【知识点】分母有理化
19.【答案】(1);
(2)
【知识点】分母有理化
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【湘教版数学八年级上册同步练习】
5.2二次根式的乘法和除法
一、单选题
1.墨迹覆盖了等式“”中的运算符号,则覆盖的是( )
A.+ B.- C.× D.÷
2.计算×的结果为( )
A. B.2 C. D.6
3. × =( )
A.2 B.4 C.2+ D.2
4.下列各式中,与 的积为有理数的是( )
A. B. C. D.
5.已知 ,则 的关系是( )
A. B. C. D.
二、填空题
6. 化简: .
7.计算: .
8.化简:(7-5 )2000·(-7-5 )2001= .
9.计算的正确结果是 .
10.计算的结果为 ,这个数落在了数轴上的 段.
11.计算 .
三、计算题
12.化简,求值:(),其中.
13.阅读下列材料,然后回答问题:
在进行二次根式运算时,我们有时会碰上如 、 这样的式子,其实我们还可以将其进一步化简:
;
.
以上这种化简的步骤叫做分母有理化.
还可以用以下方法化简:
.
(1)请用两种方法化简 ;
(2)化简: .
14.阅读下列材料,然后回答问题:
在进行类似于二次根式 的运算时,通常有如下两种方法将其进一步化简:
方法一:
方法二:
(1)请用两种不同的方法化简: ;
(2)化简: .
四、解答题
15.类比和转化是数学中解决新的问题时最常用的数学思想方法.
【学习新知,类比求解】解方程:.
解:去根号,两边同时平方得一元一次方程______,解这个方程,得______.经检验,______是原方程的解.
【学会转化,解决问题】运用上面的方法解下列方程:
(1);
(2).
五、综合题
16.综合题
(1)试比较 与 的大小;
(2)你能比较 与 的大小吗?其中k为正整数.
17.我们知道,若两个有理数的积是1,则称这两个有理数互为倒数.同样的当两个实数 与 的积是1时,我们仍然称这两个实数互为倒数.
(1)判断 与 是否互为倒数,并说明理由;
(2)若实数 是 的倒数,求x和y之间的关系.
18.已知x=2﹣ ,y=2+ ,求代数式的值:
(1)x2+2xy+y2;
(2)x2﹣y2.
六、实践探究题
19.先观察下列的等式,再回答问题:
(1)请你直接写出结果: = , = ;
(2)根据你的观察猜想: = (n为正整数).
答案解析部分
1.【答案】D
【知识点】二次根式的乘除法
2.【答案】A
【知识点】二次根式的乘除法
3.【答案】A
【知识点】二次根式的乘除法
4.【答案】D
【知识点】平方差公式及应用;二次根式的乘除法
5.【答案】D
【知识点】分母有理化
6.【答案】##
【知识点】分母有理化
7.【答案】6
【知识点】二次根式的乘除法
8.【答案】-7-5
【知识点】二次根式的乘除法
9.【答案】
【知识点】二次根式的乘除法
10.【答案】;④
【知识点】无理数在数轴上表示;二次根式的乘除法
11.【答案】5
【知识点】二次根式的乘除法
12.【答案】
【知识点】分式的化简求值;分母有理化
13.【答案】(1)解:原式=
(2)解:原式= ;(2)
= =
=
=
【知识点】分母有理化
14.【答案】(1)解:方法一:
方法二:
(2)解:原式=
【知识点】分母有理化;探索数与式的规律
15.【答案】学习新知,类比求解:,,
(1),(2)
【知识点】完全平方公式及运用;二次根式的乘除法
16.【答案】(1)解: ,
,
故 <
(2)解: ,
,
故 <
【知识点】二次根式的性质与化简;二次根式的乘除法
17.【答案】(1)解:因为(4+ )(4- )=16-2=14 1,所以4+ 与4- 不互为倒数
(2)解:因为( + )( - )=x-y,所以当x-y=1时,此两数互为倒数
【知识点】有理数的倒数;平方差公式及应用;二次根式的乘除法
18.【答案】(1)解:x2+2xy+y2
=(x+y)2
=[(2﹣ )+(2+ )]2
=42
=16;
(2)解:x2﹣y2=(x+y)(x﹣y)
=(2﹣ +2+ )(2﹣ ﹣2﹣ )
=4×(﹣2 )
=﹣8 .
【知识点】分母有理化
19.【答案】(1);
(2)
【知识点】分母有理化
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
