【湘教版数学八年级上册同步练习】 期中综合复习题(含答案)
文档属性
| 名称 | 【湘教版数学八年级上册同步练习】 期中综合复习题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-12 18:20:08 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【湘教版数学八年级上册同步练习】
期中综合复习题
一、单选题
1.潮州市的广济桥是中国古代著名桥梁之一,如图中的照片是某处栏杆的拐角,若,,则的度数为( )
A. B. C. D.
2.如图,在△ABC中,∠A=35°,∠C=45°,则与∠ABC相邻的外角的度数是( )
A.35° B.45° C.80° D.100°
3.下列说法正确的是( )
A.绝对值等于它本身的有理数只有0
B.相反数等于它本身的有理数只有0
C.倒数等于它本身的有理数有1
D.平方根等于它本身的有理数为0和+1
4.若,下列计算正确的是( )
A. B. C. D.
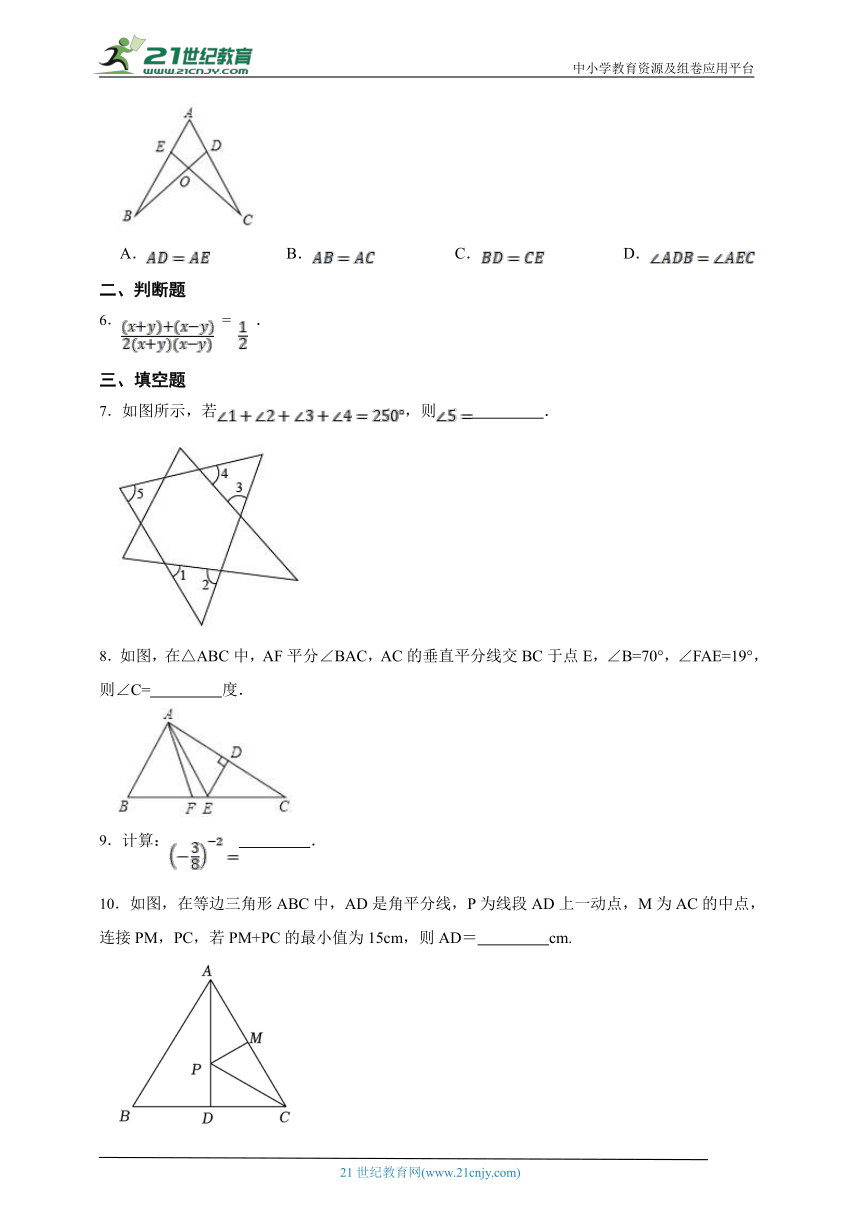
5.如图,点,分别在,上,与相交于点,已知,现添加下面的哪一个条件后,仍不能判定≌的是( )
A. B. C. D.
二、判断题
6. = .
三、填空题
7.如图所示,若,则 .
8.如图,在△ABC中,AF平分∠BAC,AC的垂直平分线交BC于点E,∠B=70°,∠FAE=19°,则∠C= 度.
9.计算: .
10.如图,在等边三角形ABC中,AD是角平分线,P为线段AD上一动点,M为AC的中点,连接PM,PC,若PM+PC的最小值为15cm,则AD= cm.
11.已知AD,AE分别是△ABC的高线和中线,若BD=2,CD=1,则DE的长为 .
12.若正数a,b,c满足abc=1,,则 .
四、计算题
13.已知3m=4,3n=5,分别求3m+n与32m﹣n的值.
14.解方程:
15.已知abc≠0且a+b+c=0,求a +b +c 的值.
五、解答题
16.先化简,再求值: ,其中
17.如图,已知AC=AD,∠CAB=∠DAB,求证:BC=BD.
18.对于两个不相等的非零实数m、n,分式的值为零,则或,又因为,所以关于x的方程有两个解,分别为,.应用上面的结论解答下列问题:
(1)方程有两个解,分别为________,________;
(2)关于x的方程的两个解分别为,,若与互为倒数且,则________,________;
(3)关于x的方程的两个解分别为,(),求的值.
六、综合题
19.某单位需要在规定时间内生产一批物资,通过调研,发现投标的工厂中有甲、乙两家资质合格,并获得如下信息:
信息1:甲厂单独完成这项任务刚好如期完成;
信息2:乙厂单独完成这项任务比规定时间多用5天;
信息3:甲、乙两厂的生产速度之比为;
根据以上信息解决下列问题:
(1)求规定时间;
(2)若甲乙两厂合作一些天后,余下的工程由乙厂单独做也正好如期完成.求甲乙两厂合作的时间.
20.如图,已知△ABC,∠C=90°,AC<BC,D为BC上一点,且到A,B两点距离相等.
(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);
(2)连结AD,若∠B=40°,求∠CAD的度数.
21.如图,在同一平面内,点D、E是△ABC外的两点,请按要求完成下列问题.(此题作图不要求写出画法)
(1)请你判断线段与AC的数量关系是 ,理由是 .
(2)连接线段CD,作射线BE、直线DE,在四边形BCDE的边BC、CD、DE、EB上任取一点,分别为点K、L、M、N并顺次连接它们,则四边形KLMN的周长与四边形BCDE周长哪一个大,直接写出结果(不用说出理由).
(3)在四边形KLMN内找一点O,使它到四边形四个顶点的距离之和最小(作图找到点即可).
七、实践探究题
22.阅读材料:学习了无理数后,某数学兴趣小组开展了一次探究活动:估算的近似值.
小明的方法:
∵,设,
∴.∴.
∴,解得.∴.
(上述方法中使用了完全平方公式:,下面可参考使用)问题:
(1)请你依照小明的方法,估算的值(结果保留两位小数);
(2)请结合上述具体实例,概括出估算的公式:已知非负整数a、b、,且,估计的值(用含a、b的代数式表示);
(3)请用(2)中的结论估算的近似值.
答案解析部分
1.【答案】C
【知识点】平行线的性质;三角形的外角性质
2.【答案】C
【知识点】三角形的外角性质
3.【答案】B
【知识点】相反数及有理数的相反数;绝对值及有理数的绝对值;有理数的倒数;平方根
4.【答案】A
【知识点】同底数幂的除法;零指数幂;负整数指数幂;同类项的概念
5.【答案】D
【知识点】三角形全等的判定
6.【答案】错误
【知识点】分式的约分
7.【答案】70°
【知识点】三角形内角和定理
8.【答案】24
【知识点】三角形内角和定理;线段垂直平分线的性质
9.【答案】
【知识点】负整数指数幂
10.【答案】15
【知识点】等边三角形的性质;轴对称的应用-最短距离问题
11.【答案】0.5或1.5
【知识点】三角形的角平分线、中线和高
12.【答案】
【知识点】分式的加减法;解分式方程
13.【答案】解:;
.
【知识点】同底数幂的除法;幂的乘方运算
14.【答案】解:
去分母得,
解得,x=3,
经检验,x=3是原方程的根,
所以,原方程的根为:x=3.
【知识点】解分式方程
15.【答案】解法一:∵abc≠0,∴a≠0,b≠0,c≠0.∴原式=a( )+b( )+c( )-3=( )(a+b+c)-3.∵a+b+c=0,∴原式=-3.解法二:a +b +c = + + + + + =( + )+( + )+( + )= + + .∵a+b+c=0,∴-a=b+c,-b=a+c,-c=a+b.∴原式= + + =-3
【知识点】分式的加减法
16.【答案】解:原式=.
=
∵x=2017,
∴原式=
=
【知识点】分式的化简求值
17.【答案】证明:在△ACB和△ADB中,
,
∴△ACB≌△ADB(AAS),
∴BC=BD
【知识点】全等三角形的判定与性质
18.【答案】(1)1,6
(2),2
(3)
【知识点】解分式方程
19.【答案】(1)规定时间是20天;
(2)甲、乙两厂合作的时间是4天.
【知识点】分式方程的实际应用;一元一次方程的实际应用-工程问题
20.【答案】(1)解:如图,点D为所作;
(2)解:△ABC中,∵∠C=90°,∠B=40°,
∴∠BAC=50°,
∵AD=BD,
∴∠B=∠BAD=40°,
∴∠CAD=∠BAC﹣∠BAD=10°.
【知识点】三角形内角和定理;线段垂直平分线的性质;等腰三角形的性质;尺规作图-垂直平分线
21.【答案】(1)AB+BC>AC;三角形的两边之和之和大于第三边
(2)解:如图,线段CD,射线BE,直线DE,四边形KLMN即为所求.四边形KLMN的周长小于四边形BCDE周长.
理由是:在△EMN和△BNK和△DLM和△CLK中,
EM+EN>MN,BN+BK>KN,DM+DL>ML,CK+CL>KL,
∴EN+EM+DM+DL+BN+BK+CL+CK>MN+NK+ML+KL,
即四边形KLMN的周长小于四边形BCDE周长.
(3)解:如图,连接NL,MK,交于点O,点O即为所求,
根据两点之间,线段最短可得:NL≥ON+OL,MK≥MO+KO,
∴点O到四个顶点的距离最短.
【知识点】三角形三边关系;尺规作图-直线、射线、线段
22.【答案】(1)解:∵,
设,
∴,
∴,
∴.
解得,
∴;
(2)解:设,
∴,
∵,
∴,
解得,
∴;
(3)解:∵,
∴.
【知识点】无理数的估值;完全平方公式及运用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【湘教版数学八年级上册同步练习】
期中综合复习题
一、单选题
1.潮州市的广济桥是中国古代著名桥梁之一,如图中的照片是某处栏杆的拐角,若,,则的度数为( )
A. B. C. D.
2.如图,在△ABC中,∠A=35°,∠C=45°,则与∠ABC相邻的外角的度数是( )
A.35° B.45° C.80° D.100°
3.下列说法正确的是( )
A.绝对值等于它本身的有理数只有0
B.相反数等于它本身的有理数只有0
C.倒数等于它本身的有理数有1
D.平方根等于它本身的有理数为0和+1
4.若,下列计算正确的是( )
A. B. C. D.
5.如图,点,分别在,上,与相交于点,已知,现添加下面的哪一个条件后,仍不能判定≌的是( )
A. B. C. D.
二、判断题
6. = .
三、填空题
7.如图所示,若,则 .
8.如图,在△ABC中,AF平分∠BAC,AC的垂直平分线交BC于点E,∠B=70°,∠FAE=19°,则∠C= 度.
9.计算: .
10.如图,在等边三角形ABC中,AD是角平分线,P为线段AD上一动点,M为AC的中点,连接PM,PC,若PM+PC的最小值为15cm,则AD= cm.
11.已知AD,AE分别是△ABC的高线和中线,若BD=2,CD=1,则DE的长为 .
12.若正数a,b,c满足abc=1,,则 .
四、计算题
13.已知3m=4,3n=5,分别求3m+n与32m﹣n的值.
14.解方程:
15.已知abc≠0且a+b+c=0,求a +b +c 的值.
五、解答题
16.先化简,再求值: ,其中
17.如图,已知AC=AD,∠CAB=∠DAB,求证:BC=BD.
18.对于两个不相等的非零实数m、n,分式的值为零,则或,又因为,所以关于x的方程有两个解,分别为,.应用上面的结论解答下列问题:
(1)方程有两个解,分别为________,________;
(2)关于x的方程的两个解分别为,,若与互为倒数且,则________,________;
(3)关于x的方程的两个解分别为,(),求的值.
六、综合题
19.某单位需要在规定时间内生产一批物资,通过调研,发现投标的工厂中有甲、乙两家资质合格,并获得如下信息:
信息1:甲厂单独完成这项任务刚好如期完成;
信息2:乙厂单独完成这项任务比规定时间多用5天;
信息3:甲、乙两厂的生产速度之比为;
根据以上信息解决下列问题:
(1)求规定时间;
(2)若甲乙两厂合作一些天后,余下的工程由乙厂单独做也正好如期完成.求甲乙两厂合作的时间.
20.如图,已知△ABC,∠C=90°,AC<BC,D为BC上一点,且到A,B两点距离相等.
(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);
(2)连结AD,若∠B=40°,求∠CAD的度数.
21.如图,在同一平面内,点D、E是△ABC外的两点,请按要求完成下列问题.(此题作图不要求写出画法)
(1)请你判断线段与AC的数量关系是 ,理由是 .
(2)连接线段CD,作射线BE、直线DE,在四边形BCDE的边BC、CD、DE、EB上任取一点,分别为点K、L、M、N并顺次连接它们,则四边形KLMN的周长与四边形BCDE周长哪一个大,直接写出结果(不用说出理由).
(3)在四边形KLMN内找一点O,使它到四边形四个顶点的距离之和最小(作图找到点即可).
七、实践探究题
22.阅读材料:学习了无理数后,某数学兴趣小组开展了一次探究活动:估算的近似值.
小明的方法:
∵,设,
∴.∴.
∴,解得.∴.
(上述方法中使用了完全平方公式:,下面可参考使用)问题:
(1)请你依照小明的方法,估算的值(结果保留两位小数);
(2)请结合上述具体实例,概括出估算的公式:已知非负整数a、b、,且,估计的值(用含a、b的代数式表示);
(3)请用(2)中的结论估算的近似值.
答案解析部分
1.【答案】C
【知识点】平行线的性质;三角形的外角性质
2.【答案】C
【知识点】三角形的外角性质
3.【答案】B
【知识点】相反数及有理数的相反数;绝对值及有理数的绝对值;有理数的倒数;平方根
4.【答案】A
【知识点】同底数幂的除法;零指数幂;负整数指数幂;同类项的概念
5.【答案】D
【知识点】三角形全等的判定
6.【答案】错误
【知识点】分式的约分
7.【答案】70°
【知识点】三角形内角和定理
8.【答案】24
【知识点】三角形内角和定理;线段垂直平分线的性质
9.【答案】
【知识点】负整数指数幂
10.【答案】15
【知识点】等边三角形的性质;轴对称的应用-最短距离问题
11.【答案】0.5或1.5
【知识点】三角形的角平分线、中线和高
12.【答案】
【知识点】分式的加减法;解分式方程
13.【答案】解:;
.
【知识点】同底数幂的除法;幂的乘方运算
14.【答案】解:
去分母得,
解得,x=3,
经检验,x=3是原方程的根,
所以,原方程的根为:x=3.
【知识点】解分式方程
15.【答案】解法一:∵abc≠0,∴a≠0,b≠0,c≠0.∴原式=a( )+b( )+c( )-3=( )(a+b+c)-3.∵a+b+c=0,∴原式=-3.解法二:a +b +c = + + + + + =( + )+( + )+( + )= + + .∵a+b+c=0,∴-a=b+c,-b=a+c,-c=a+b.∴原式= + + =-3
【知识点】分式的加减法
16.【答案】解:原式=.
=
∵x=2017,
∴原式=
=
【知识点】分式的化简求值
17.【答案】证明:在△ACB和△ADB中,
,
∴△ACB≌△ADB(AAS),
∴BC=BD
【知识点】全等三角形的判定与性质
18.【答案】(1)1,6
(2),2
(3)
【知识点】解分式方程
19.【答案】(1)规定时间是20天;
(2)甲、乙两厂合作的时间是4天.
【知识点】分式方程的实际应用;一元一次方程的实际应用-工程问题
20.【答案】(1)解:如图,点D为所作;
(2)解:△ABC中,∵∠C=90°,∠B=40°,
∴∠BAC=50°,
∵AD=BD,
∴∠B=∠BAD=40°,
∴∠CAD=∠BAC﹣∠BAD=10°.
【知识点】三角形内角和定理;线段垂直平分线的性质;等腰三角形的性质;尺规作图-垂直平分线
21.【答案】(1)AB+BC>AC;三角形的两边之和之和大于第三边
(2)解:如图,线段CD,射线BE,直线DE,四边形KLMN即为所求.四边形KLMN的周长小于四边形BCDE周长.
理由是:在△EMN和△BNK和△DLM和△CLK中,
EM+EN>MN,BN+BK>KN,DM+DL>ML,CK+CL>KL,
∴EN+EM+DM+DL+BN+BK+CL+CK>MN+NK+ML+KL,
即四边形KLMN的周长小于四边形BCDE周长.
(3)解:如图,连接NL,MK,交于点O,点O即为所求,
根据两点之间,线段最短可得:NL≥ON+OL,MK≥MO+KO,
∴点O到四个顶点的距离最短.
【知识点】三角形三边关系;尺规作图-直线、射线、线段
22.【答案】(1)解:∵,
设,
∴,
∴,
∴.
解得,
∴;
(2)解:设,
∴,
∵,
∴,
解得,
∴;
(3)解:∵,
∴.
【知识点】无理数的估值;完全平方公式及运用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
