【湘教版数学九年级上册同步练习】 第一章反比例函数检测题(含答案)
文档属性
| 名称 | 【湘教版数学九年级上册同步练习】 第一章反比例函数检测题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-12 18:09:29 | ||
图片预览

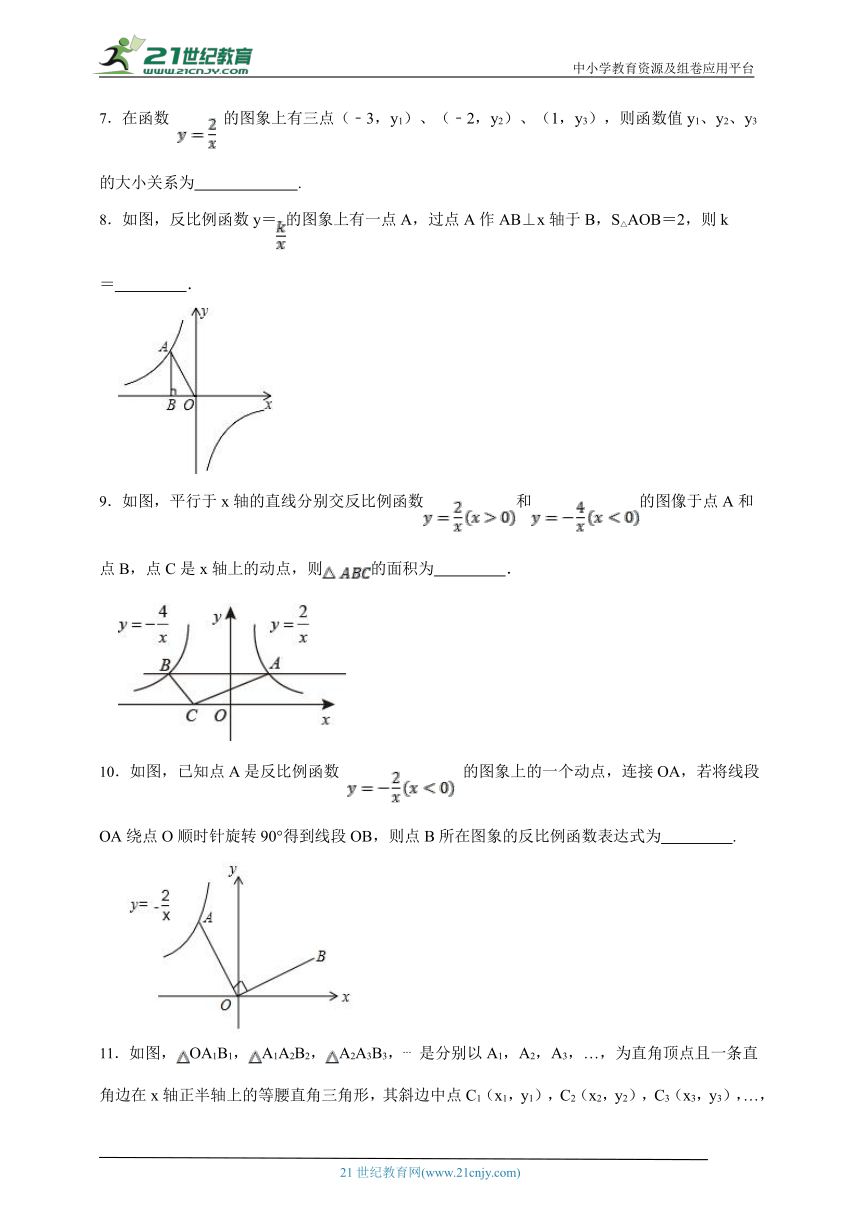
文档简介
中小学教育资源及组卷应用平台
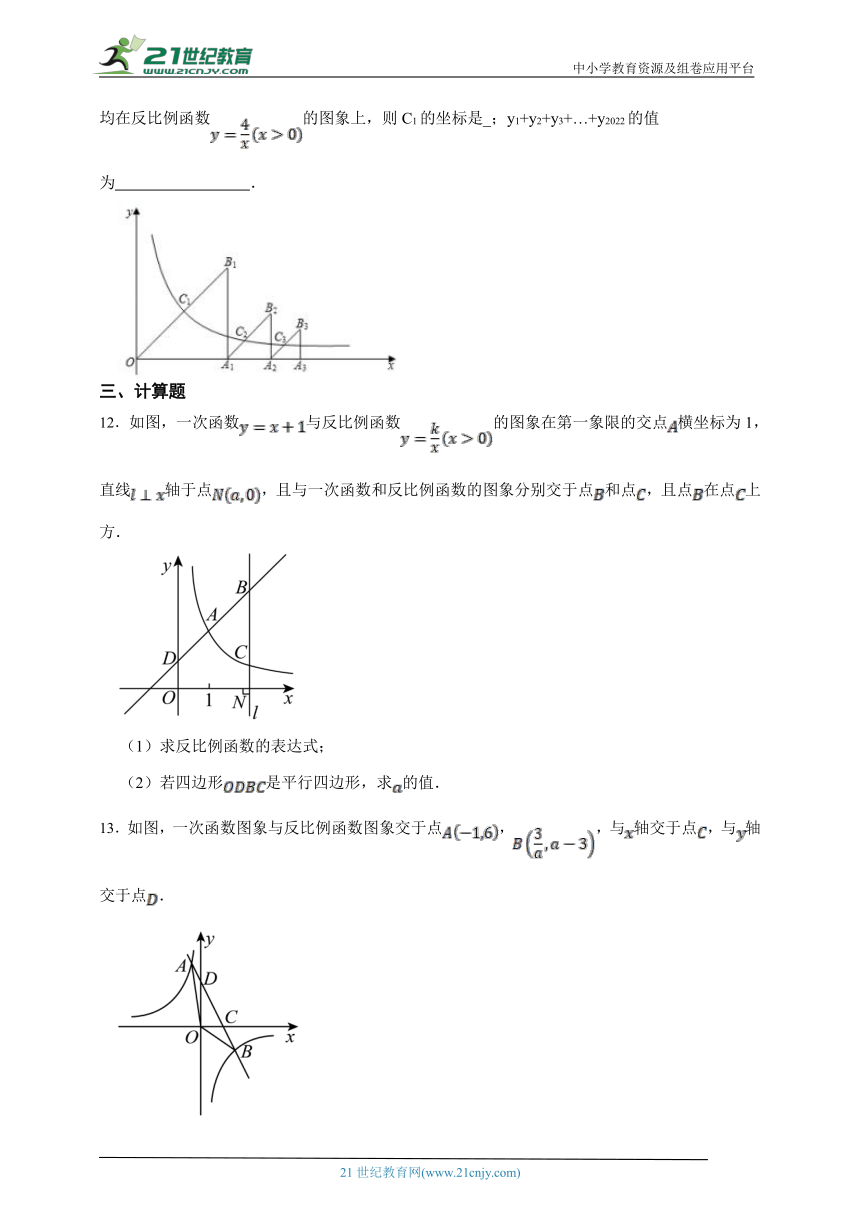
【湘教版数学九年级上册同步练习】
第一章反比例函数检测题
一、单选题
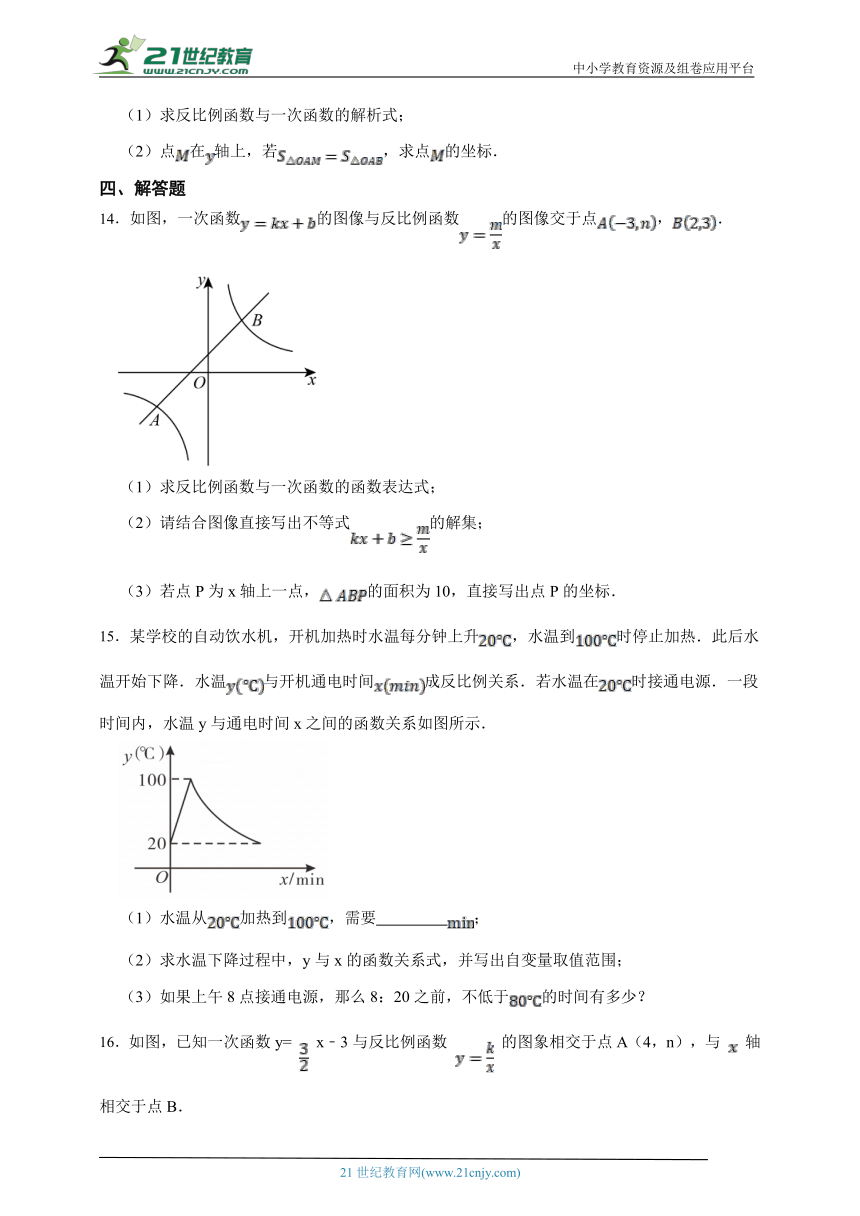
1.如果y是x的反比例函数,那么当x增加它的时,y将( )
A.减少它的 B.减少它的 C.增加它的 D.增加它的
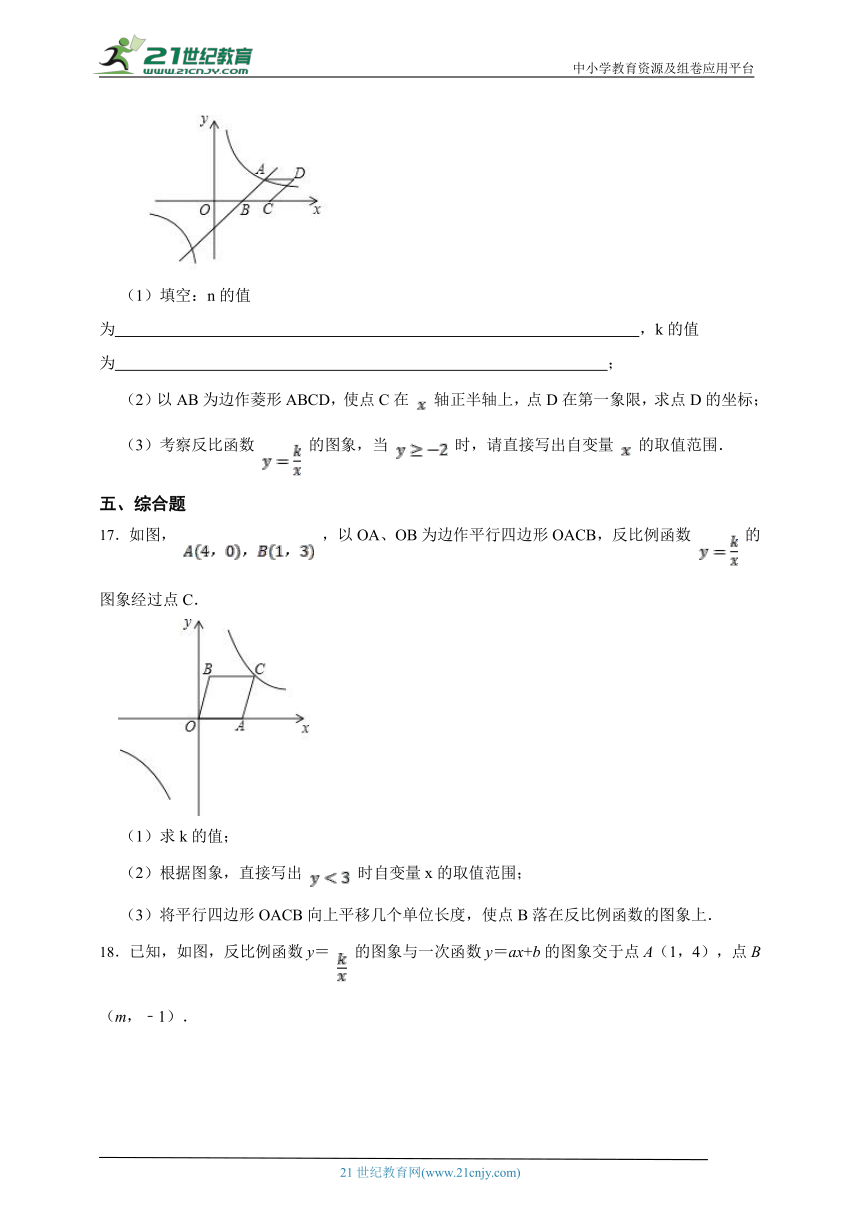
2.下列函数是 关于 的反比例函数的是( )
A. B. C. D.
3.反比例函数的比例系数为( )
A. B.-3 C.-5 D.
4.如图,点A的反比例函数y= (x>0)的图象上,点B在反比例函数y= (x>0)的图象上,AB∥x轴,BC⊥x轴,垂足为C,连接AC,若△ABC的面积是6,则k的值为( )
A.10 B.12 C.14 D.16
5.反比例函数图像上有两个点,,,则的图像不经过第( )象限
A.一 B.二 C.三 D.四
二、填空题
6.写出一个图象位于二、四象限的反比例函数的表达式,y= .
7.在函数 的图象上有三点(﹣3,y1)、(﹣2,y2)、(1,y3),则函数值y1、y2、y3的大小关系为 .
8.如图,反比例函数y=的图象上有一点A,过点A作AB⊥x轴于B,S△AOB=2,则k= .
9.如图,平行于x轴的直线分别交反比例函数和的图像于点A和点B,点C是x轴上的动点,则的面积为 .
10.如图,已知点A是反比例函数 的图象上的一个动点,连接OA,若将线段OA绕点O顺时针旋转90°得到线段OB,则点B所在图象的反比例函数表达式为 .
11.如图,OA1B1,A1A2B2,A2A3B3, 是分别以A1,A2,A3,…,为直角顶点且一条直角边在x轴正半轴上的等腰直角三角形,其斜边中点C1(x1,y1),C2(x2,y2),C3(x3,y3),…,均在反比例函数的图象上,则C1的坐标是_;y1+y2+y3+…+y2022的值为 .
三、计算题
12.如图,一次函数与反比例函数的图象在第一象限的交点横坐标为1,直线轴于点,且与一次函数和反比例函数的图象分别交于点和点,且点在点上方.
(1)求反比例函数的表达式;
(2)若四边形是平行四边形,求的值.
13.如图,一次函数图象与反比例函数图象交于点,,与轴交于点,与轴交于点.
(1)求反比例函数与一次函数的解析式;
(2)点在轴上,若,求点的坐标.
四、解答题
14.如图,一次函数的图像与反比例函数的图像交于点,.
(1)求反比例函数与一次函数的函数表达式;
(2)请结合图像直接写出不等式的解集;
(3)若点P为x轴上一点,的面积为10,直接写出点P的坐标.
15.某学校的自动饮水机,开机加热时水温每分钟上升,水温到时停止加热.此后水温开始下降.水温与开机通电时间成反比例关系.若水温在时接通电源.一段时间内,水温y与通电时间x之间的函数关系如图所示.
(1)水温从加热到,需要 ;
(2)求水温下降过程中,y与x的函数关系式,并写出自变量取值范围;
(3)如果上午8点接通电源,那么8:20之前,不低于的时间有多少?
16.如图,已知一次函数y= x﹣3与反比例函数 的图象相交于点A(4,n),与 轴相交于点B.
(1)填空:n的值为 ,k的值为 ;
(2)以AB为边作菱形ABCD,使点C在 轴正半轴上,点D在第一象限,求点D的坐标;
(3)考察反比函数 的图象,当 时,请直接写出自变量 的取值范围.
五、综合题
17.如图, ,以OA、OB为边作平行四边形OACB,反比例函数 的图象经过点C.
(1)求k的值;
(2)根据图象,直接写出 时自变量x的取值范围;
(3)将平行四边形OACB向上平移几个单位长度,使点B落在反比例函数的图象上.
18.已知,如图,反比例函数y= 的图象与一次函数y=ax+b的图象交于点A(1,4),点B(m,﹣1).
(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出不等式ax+b≥ 的解集是 .
19.如图,在△ABC中,CA=CB=5,AB=6,AB⊥y轴,垂足为A.反比例函数y= (x>0)的图象经过点C,交AB于点D.
(1)若OA=8,求k的值;
(2)若CB=BD,求点C的坐标.
六、实践探究题
20.确定有效消毒的时间段
背景素材
预防传染病,某校定期对教室进行“药熏消毒”.已知药物释放阶段,室内每立方米空气中的含药量y(mg)与释放时间x(min)成一次函数;释放后,y与x成反比例如图1所示,且2min时,室内每立方米空气中的含药量y(mg)达到最大值.某兴趣小组记录部分y(mg)与x(min)的测量数据如表1.满足的自变量x(min)的取值范围为有效消毒时间段.
x … 0.5 1 1.5 2 2.5 3 …
y … 2.5 3 3.5 4 3.2 2.67 …
问题解决
(1)任务1
确定y关于x的一次函数及反比例函数的表达式.
(2)任务2
初步确定有效消毒时间段即自变量x的取值范围.
(3)任务3
若实际生活中有效消毒时间段要求满足a≤x≤3a,其中a为常数,请确定实际生活中有效消毒的时间段.
答案解析部分
1.【答案】B
【知识点】反比例函数的概念
2.【答案】C
【知识点】反比例函数的概念
3.【答案】A
【知识点】反比例函数的概念
4.【答案】D
【知识点】反比例函数系数k的几何意义
5.【答案】B
【知识点】反比例函数的性质;反比例函数与一次函数的交点问题;一次函数图象、性质与系数的关系
6.【答案】y=﹣x
【知识点】反比例函数的性质
7.【答案】
【知识点】反比例函数图象上点的坐标特征
8.【答案】-4
【知识点】反比例函数系数k的几何意义
9.【答案】3
【知识点】反比例函数系数k的几何意义
10.【答案】
【知识点】反比例函数的性质;全等三角形的判定与性质;旋转的性质
11.【答案】
【知识点】探索数与式的规律;反比例函数图象上点的坐标特征
12.【答案】(1)
(2)
【知识点】反比例函数与一次函数的交点问题;平行四边形的性质
13.【答案】(1),
(2)或
【知识点】待定系数法求一次函数解析式;待定系数法求反比例函数解析式;反比例函数与一次函数的交点问题
14.【答案】(1)反比例函数的解析式为y=,一次函数的解析式为y=x+1;
(2)-3≤x<0或x≥2;
(3)P的坐标是(-5,0)或(3,0).
【知识点】坐标与图形性质;待定系数法求一次函数解析式;反比例函数与一次函数的交点问题
15.【答案】(1)4
(2)解:如图设函数解析式为
代入点可得,
当时,,
水温下降过程中,与的函数关系式是
(3)解:由计算可知,水温从开始加热到再冷却到
需分钟
水温从加热到所需要时间为:(分钟)
令,则
水温不低于的时间为(分钟)
答:不低于的时间有2分钟.
【知识点】反比例函数的实际应用
16.【答案】(1)解:把点A(4,n)代入一次函数y=x﹣3,可得n=×4﹣3=3;;把点A(4,3)代入反比例函数y=,可得3=,解得k=12;
(2)解:∵一次函数y=x﹣3与x轴相交于点B, ∴x﹣3=0,解得x=2,∴点B的坐标为(2,0);
如图,过点A作AE⊥x轴,垂足为E,过点D作DF⊥x轴,垂足为F,
∵A(4,3),B(2,0),∴OE=4,AE=3,OB=2,∴BE=OE﹣OB=4﹣2=2,在Rt△ABE中,AB===,∵四边形ABCD是菱形,∴AB=CD=BC=,∵AB∥CD,∴∠ABE=∠DCF,∵AE⊥x轴,DF⊥x轴,∴∠AEB=∠DFC=90°,
在△ABE与△DCF中,
∴△ABE≌△DCF(ASA),
∴CF=BE=2,DF=AE=3;∴OF=OB+BC+CF=2++2=4+,
∴点D的坐标为(4+,3)
(3)解:当y=﹣2时,﹣2=,解得x=﹣6.
故当y≥﹣2时,自变量x的取值范围是x≤﹣6或x>0.
【知识点】反比例函数的性质;待定系数法求反比例函数解析式;反比例函数的实际应用;全等三角形的判定与性质;菱形的性质
17.【答案】(1)解: 平行四边形OACB中, ,
,
把 代入 ,得: ,
解得:
(2)解: 时自变量x的取值范围为: 或
(3)解:把 代入 ,
解得: ,
向上平移 个单位
【知识点】坐标与图形性质;待定系数法求反比例函数解析式;平行四边形的性质
18.【答案】(1)解:∵y= 函数的图象过点A(1,4),
∴k=4,即y= ,
又∵点B(m,﹣1)在y= 上,
∴m=﹣4,
∴B(﹣4,﹣1),
∵一次函数y=ax+b过A、B两点,
即 ,
解得: ,
∴y=x+3;
(2)解:由y=x+3可知C(﹣3,0),
∴S△OAB=S△OAC+S△OBC= ×3×4+ ×3×1= .
(3)﹣4≤x<0或x≥1
【知识点】待定系数法求一次函数解析式;待定系数法求反比例函数解析式;反比例函数与一次函数的交点问题;三角形的面积
19.【答案】(1)解:过C作CM⊥AB,CN⊥y轴,垂足为M、N,
∵CA=CB=5,AB=6,
∴AM=MB=3=CN,
在Rt△ACD中,CD= =4,
∴AN=4,ON=OA﹣AN=8﹣4=4,
∴C(3,4)代入y= 得:k=12,
答:k的值为12.
(2)解:∵BC=BD=5,
∴AD=6﹣5=1,
设OA=a,则ON=a﹣4,C(3,a﹣4),D(1,a)
∵点C、D在反比例函数的图象上,
∴3(a﹣4)=1×a,
解得:a=6,
∴C(3,2)
答:点C的坐标为(3,2)
【知识点】反比例函数的图象;勾股定理
20.【答案】(1)解:设当药物释放阶段(即0≤x≤2)时,设y=kx+b,把,代入y=kx+b,
得,解得,
∴;
设当药物释放后(即x≥2)时,设,把代入,得,
解得.
(2)解:把分别代入,得,
解得,
由图象,得.
(3)解:⑴当3a≤2时,
把代入y=x+2,得,解得;
把x=3a=2代入y=x+2,得y=4,满足题意;
.
⑵a≥2时,把代入,得,解得a=1(舍去);
∴无解.
⑶a≤2≤3a时,(即)
①把代入y=x+2,得解得;
把x=3a=2代入,解得y=4,满足要求(),
∴.
②把代入,得,解得a=1;
把x=a=1代入y=x+2,解得y=3,满足要求(),
∴1(min)≤x≤3(min).
综上,,或1(min)≤x≤3(min).
【知识点】反比例函数与一次函数的交点问题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【湘教版数学九年级上册同步练习】
第一章反比例函数检测题
一、单选题
1.如果y是x的反比例函数,那么当x增加它的时,y将( )
A.减少它的 B.减少它的 C.增加它的 D.增加它的
2.下列函数是 关于 的反比例函数的是( )
A. B. C. D.
3.反比例函数的比例系数为( )
A. B.-3 C.-5 D.
4.如图,点A的反比例函数y= (x>0)的图象上,点B在反比例函数y= (x>0)的图象上,AB∥x轴,BC⊥x轴,垂足为C,连接AC,若△ABC的面积是6,则k的值为( )
A.10 B.12 C.14 D.16
5.反比例函数图像上有两个点,,,则的图像不经过第( )象限
A.一 B.二 C.三 D.四
二、填空题
6.写出一个图象位于二、四象限的反比例函数的表达式,y= .
7.在函数 的图象上有三点(﹣3,y1)、(﹣2,y2)、(1,y3),则函数值y1、y2、y3的大小关系为 .
8.如图,反比例函数y=的图象上有一点A,过点A作AB⊥x轴于B,S△AOB=2,则k= .
9.如图,平行于x轴的直线分别交反比例函数和的图像于点A和点B,点C是x轴上的动点,则的面积为 .
10.如图,已知点A是反比例函数 的图象上的一个动点,连接OA,若将线段OA绕点O顺时针旋转90°得到线段OB,则点B所在图象的反比例函数表达式为 .
11.如图,OA1B1,A1A2B2,A2A3B3, 是分别以A1,A2,A3,…,为直角顶点且一条直角边在x轴正半轴上的等腰直角三角形,其斜边中点C1(x1,y1),C2(x2,y2),C3(x3,y3),…,均在反比例函数的图象上,则C1的坐标是_;y1+y2+y3+…+y2022的值为 .
三、计算题
12.如图,一次函数与反比例函数的图象在第一象限的交点横坐标为1,直线轴于点,且与一次函数和反比例函数的图象分别交于点和点,且点在点上方.
(1)求反比例函数的表达式;
(2)若四边形是平行四边形,求的值.
13.如图,一次函数图象与反比例函数图象交于点,,与轴交于点,与轴交于点.
(1)求反比例函数与一次函数的解析式;
(2)点在轴上,若,求点的坐标.
四、解答题
14.如图,一次函数的图像与反比例函数的图像交于点,.
(1)求反比例函数与一次函数的函数表达式;
(2)请结合图像直接写出不等式的解集;
(3)若点P为x轴上一点,的面积为10,直接写出点P的坐标.
15.某学校的自动饮水机,开机加热时水温每分钟上升,水温到时停止加热.此后水温开始下降.水温与开机通电时间成反比例关系.若水温在时接通电源.一段时间内,水温y与通电时间x之间的函数关系如图所示.
(1)水温从加热到,需要 ;
(2)求水温下降过程中,y与x的函数关系式,并写出自变量取值范围;
(3)如果上午8点接通电源,那么8:20之前,不低于的时间有多少?
16.如图,已知一次函数y= x﹣3与反比例函数 的图象相交于点A(4,n),与 轴相交于点B.
(1)填空:n的值为 ,k的值为 ;
(2)以AB为边作菱形ABCD,使点C在 轴正半轴上,点D在第一象限,求点D的坐标;
(3)考察反比函数 的图象,当 时,请直接写出自变量 的取值范围.
五、综合题
17.如图, ,以OA、OB为边作平行四边形OACB,反比例函数 的图象经过点C.
(1)求k的值;
(2)根据图象,直接写出 时自变量x的取值范围;
(3)将平行四边形OACB向上平移几个单位长度,使点B落在反比例函数的图象上.
18.已知,如图,反比例函数y= 的图象与一次函数y=ax+b的图象交于点A(1,4),点B(m,﹣1).
(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出不等式ax+b≥ 的解集是 .
19.如图,在△ABC中,CA=CB=5,AB=6,AB⊥y轴,垂足为A.反比例函数y= (x>0)的图象经过点C,交AB于点D.
(1)若OA=8,求k的值;
(2)若CB=BD,求点C的坐标.
六、实践探究题
20.确定有效消毒的时间段
背景素材
预防传染病,某校定期对教室进行“药熏消毒”.已知药物释放阶段,室内每立方米空气中的含药量y(mg)与释放时间x(min)成一次函数;释放后,y与x成反比例如图1所示,且2min时,室内每立方米空气中的含药量y(mg)达到最大值.某兴趣小组记录部分y(mg)与x(min)的测量数据如表1.满足的自变量x(min)的取值范围为有效消毒时间段.
x … 0.5 1 1.5 2 2.5 3 …
y … 2.5 3 3.5 4 3.2 2.67 …
问题解决
(1)任务1
确定y关于x的一次函数及反比例函数的表达式.
(2)任务2
初步确定有效消毒时间段即自变量x的取值范围.
(3)任务3
若实际生活中有效消毒时间段要求满足a≤x≤3a,其中a为常数,请确定实际生活中有效消毒的时间段.
答案解析部分
1.【答案】B
【知识点】反比例函数的概念
2.【答案】C
【知识点】反比例函数的概念
3.【答案】A
【知识点】反比例函数的概念
4.【答案】D
【知识点】反比例函数系数k的几何意义
5.【答案】B
【知识点】反比例函数的性质;反比例函数与一次函数的交点问题;一次函数图象、性质与系数的关系
6.【答案】y=﹣x
【知识点】反比例函数的性质
7.【答案】
【知识点】反比例函数图象上点的坐标特征
8.【答案】-4
【知识点】反比例函数系数k的几何意义
9.【答案】3
【知识点】反比例函数系数k的几何意义
10.【答案】
【知识点】反比例函数的性质;全等三角形的判定与性质;旋转的性质
11.【答案】
【知识点】探索数与式的规律;反比例函数图象上点的坐标特征
12.【答案】(1)
(2)
【知识点】反比例函数与一次函数的交点问题;平行四边形的性质
13.【答案】(1),
(2)或
【知识点】待定系数法求一次函数解析式;待定系数法求反比例函数解析式;反比例函数与一次函数的交点问题
14.【答案】(1)反比例函数的解析式为y=,一次函数的解析式为y=x+1;
(2)-3≤x<0或x≥2;
(3)P的坐标是(-5,0)或(3,0).
【知识点】坐标与图形性质;待定系数法求一次函数解析式;反比例函数与一次函数的交点问题
15.【答案】(1)4
(2)解:如图设函数解析式为
代入点可得,
当时,,
水温下降过程中,与的函数关系式是
(3)解:由计算可知,水温从开始加热到再冷却到
需分钟
水温从加热到所需要时间为:(分钟)
令,则
水温不低于的时间为(分钟)
答:不低于的时间有2分钟.
【知识点】反比例函数的实际应用
16.【答案】(1)解:把点A(4,n)代入一次函数y=x﹣3,可得n=×4﹣3=3;;把点A(4,3)代入反比例函数y=,可得3=,解得k=12;
(2)解:∵一次函数y=x﹣3与x轴相交于点B, ∴x﹣3=0,解得x=2,∴点B的坐标为(2,0);
如图,过点A作AE⊥x轴,垂足为E,过点D作DF⊥x轴,垂足为F,
∵A(4,3),B(2,0),∴OE=4,AE=3,OB=2,∴BE=OE﹣OB=4﹣2=2,在Rt△ABE中,AB===,∵四边形ABCD是菱形,∴AB=CD=BC=,∵AB∥CD,∴∠ABE=∠DCF,∵AE⊥x轴,DF⊥x轴,∴∠AEB=∠DFC=90°,
在△ABE与△DCF中,
∴△ABE≌△DCF(ASA),
∴CF=BE=2,DF=AE=3;∴OF=OB+BC+CF=2++2=4+,
∴点D的坐标为(4+,3)
(3)解:当y=﹣2时,﹣2=,解得x=﹣6.
故当y≥﹣2时,自变量x的取值范围是x≤﹣6或x>0.
【知识点】反比例函数的性质;待定系数法求反比例函数解析式;反比例函数的实际应用;全等三角形的判定与性质;菱形的性质
17.【答案】(1)解: 平行四边形OACB中, ,
,
把 代入 ,得: ,
解得:
(2)解: 时自变量x的取值范围为: 或
(3)解:把 代入 ,
解得: ,
向上平移 个单位
【知识点】坐标与图形性质;待定系数法求反比例函数解析式;平行四边形的性质
18.【答案】(1)解:∵y= 函数的图象过点A(1,4),
∴k=4,即y= ,
又∵点B(m,﹣1)在y= 上,
∴m=﹣4,
∴B(﹣4,﹣1),
∵一次函数y=ax+b过A、B两点,
即 ,
解得: ,
∴y=x+3;
(2)解:由y=x+3可知C(﹣3,0),
∴S△OAB=S△OAC+S△OBC= ×3×4+ ×3×1= .
(3)﹣4≤x<0或x≥1
【知识点】待定系数法求一次函数解析式;待定系数法求反比例函数解析式;反比例函数与一次函数的交点问题;三角形的面积
19.【答案】(1)解:过C作CM⊥AB,CN⊥y轴,垂足为M、N,
∵CA=CB=5,AB=6,
∴AM=MB=3=CN,
在Rt△ACD中,CD= =4,
∴AN=4,ON=OA﹣AN=8﹣4=4,
∴C(3,4)代入y= 得:k=12,
答:k的值为12.
(2)解:∵BC=BD=5,
∴AD=6﹣5=1,
设OA=a,则ON=a﹣4,C(3,a﹣4),D(1,a)
∵点C、D在反比例函数的图象上,
∴3(a﹣4)=1×a,
解得:a=6,
∴C(3,2)
答:点C的坐标为(3,2)
【知识点】反比例函数的图象;勾股定理
20.【答案】(1)解:设当药物释放阶段(即0≤x≤2)时,设y=kx+b,把,代入y=kx+b,
得,解得,
∴;
设当药物释放后(即x≥2)时,设,把代入,得,
解得.
(2)解:把分别代入,得,
解得,
由图象,得.
(3)解:⑴当3a≤2时,
把代入y=x+2,得,解得;
把x=3a=2代入y=x+2,得y=4,满足题意;
.
⑵a≥2时,把代入,得,解得a=1(舍去);
∴无解.
⑶a≤2≤3a时,(即)
①把代入y=x+2,得解得;
把x=3a=2代入,解得y=4,满足要求(),
∴.
②把代入,得,解得a=1;
把x=a=1代入y=x+2,解得y=3,满足要求(),
∴1(min)≤x≤3(min).
综上,,或1(min)≤x≤3(min).
【知识点】反比例函数与一次函数的交点问题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
