北师大版五年级上册数学《第五单元分数的意义复习》课件(共18张PPT)
文档属性
| 名称 | 北师大版五年级上册数学《第五单元分数的意义复习》课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 712.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-12 16:06:11 | ||
图片预览






文档简介
(共18张PPT)
第五单元 分数的意义
练习六
学习目标
1. 能正确理解分数的意义;能正确用分数描述图形或简单的生活现象。
2. 能正确理解分数与除法的关系。
3. 能认识真分数、假分数,并能正确进行假分数与带分数、整数的互化。
4. 能理解、掌握分数的基本性质,并运用解决相关问题。
典型例题
考察点:分数的意义,用分数表示图形,分数单位
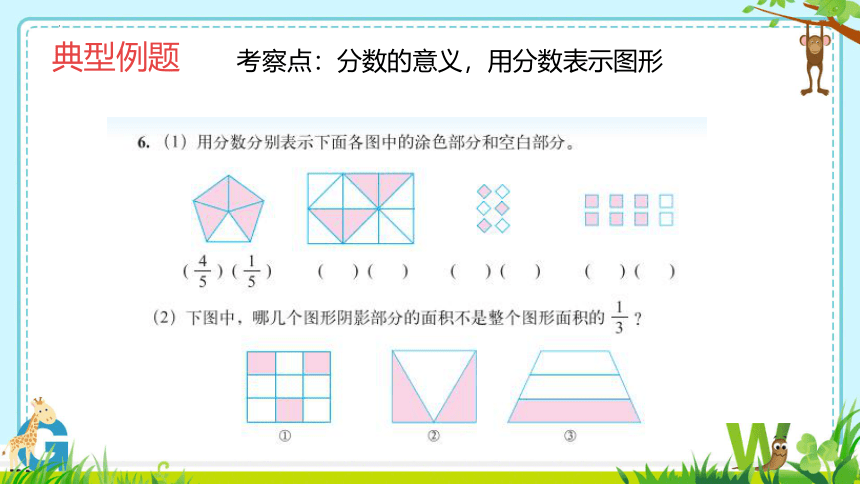
典型例题
考察点:分数的意义,用分数表示图形
典型例题
考察点:分数的意义,用分数表示生活实例
典型例题
考察点:分数的意义
知识要点:
当平均分成的份数和所占的份数不同时,同样的面积可以用不同分数表示。
典型例题
考察点:逆向理解分数的意义
知识要点:
分数的意义:把整体平均分成若干份,其中的若干份用分数表示。
典型例题
考察点:分数的意义,逆向思考
典型例题
考察点:借助数轴认识真分数、假分数
知识要点:
真分数:分子<分母;分数<1
假分数:分子≥分母;分数≥1
典型例题
考察点:真分数、假分数
知识要点:
真分数:分子<分母;分数<1
假分数:分子≥分母;分数≥1
典型例题
考察点:假分数与带分数、整数的互化
知识要点:
借助分数与除法的关系进行互化
典型例题
考察点:真分数、假分数、带分数
典型例题
考察点:分数与除法的关系;分数表示两个量之间的关系
知识要点:
分数与除法:
分数既可以表示具体的量大小,也可以表示两个量之间的关系。
典型例题
考察点:分数与除法的关系;分数表示两个量之间的关系
典型例题
考察点:分数的基本性质
知识要点:
分数的基本性质:分子分母同乘以或除以同一个不为0的数,分数大小不变。
a÷b=(a×c)÷(b×c)(b、c≠0)
a÷b=(a÷c)÷(b÷c)(b、c≠0)
典型例题
考察点:分数的基本性质
课堂小结
任选一个问题回答,进行总结反思
请你选用几个关键词概括本单元的收获。
结合本单元内容 ,你可以提出哪些问题?
请你为本节课设计一张知识卡片。
如果你是老师,你希望学生掌握什么?
请设计一个综合活动或任务,检验本单元的掌握程度。
课后作业
制作一张A4大小的数学小报,内容:
梳理本单元的分数的相关内容和知识框架
搜集整理典型例题和易错题,分析考察点、具体的方法步骤。
写出每一块内容约占这张小报的几分之几(制作之前先规划版块)
第五单元 分数的意义
练习六
学习目标
1. 能正确理解分数的意义;能正确用分数描述图形或简单的生活现象。
2. 能正确理解分数与除法的关系。
3. 能认识真分数、假分数,并能正确进行假分数与带分数、整数的互化。
4. 能理解、掌握分数的基本性质,并运用解决相关问题。
典型例题
考察点:分数的意义,用分数表示图形,分数单位
典型例题
考察点:分数的意义,用分数表示图形
典型例题
考察点:分数的意义,用分数表示生活实例
典型例题
考察点:分数的意义
知识要点:
当平均分成的份数和所占的份数不同时,同样的面积可以用不同分数表示。
典型例题
考察点:逆向理解分数的意义
知识要点:
分数的意义:把整体平均分成若干份,其中的若干份用分数表示。
典型例题
考察点:分数的意义,逆向思考
典型例题
考察点:借助数轴认识真分数、假分数
知识要点:
真分数:分子<分母;分数<1
假分数:分子≥分母;分数≥1
典型例题
考察点:真分数、假分数
知识要点:
真分数:分子<分母;分数<1
假分数:分子≥分母;分数≥1
典型例题
考察点:假分数与带分数、整数的互化
知识要点:
借助分数与除法的关系进行互化
典型例题
考察点:真分数、假分数、带分数
典型例题
考察点:分数与除法的关系;分数表示两个量之间的关系
知识要点:
分数与除法:
分数既可以表示具体的量大小,也可以表示两个量之间的关系。
典型例题
考察点:分数与除法的关系;分数表示两个量之间的关系
典型例题
考察点:分数的基本性质
知识要点:
分数的基本性质:分子分母同乘以或除以同一个不为0的数,分数大小不变。
a÷b=(a×c)÷(b×c)(b、c≠0)
a÷b=(a÷c)÷(b÷c)(b、c≠0)
典型例题
考察点:分数的基本性质
课堂小结
任选一个问题回答,进行总结反思
请你选用几个关键词概括本单元的收获。
结合本单元内容 ,你可以提出哪些问题?
请你为本节课设计一张知识卡片。
如果你是老师,你希望学生掌握什么?
请设计一个综合活动或任务,检验本单元的掌握程度。
课后作业
制作一张A4大小的数学小报,内容:
梳理本单元的分数的相关内容和知识框架
搜集整理典型例题和易错题,分析考察点、具体的方法步骤。
写出每一块内容约占这张小报的几分之几(制作之前先规划版块)
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
