4.1.2 指数函数的性质与图象 课件(共45张PPT)- 高一数学人教B版(2019)必修第二册
文档属性
| 名称 | 4.1.2 指数函数的性质与图象 课件(共45张PPT)- 高一数学人教B版(2019)必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-12 00:00:00 | ||
图片预览








文档简介
(共44张PPT)
第四章 指数函数、对数函数与幂函数
4.1.2 指数函数的性质与图象
人教B版(2019)
课标要点 核心素养
1.了解指数函数模型的实际背景 数学抽象
2.理解指数函数的概念及意义 直观想象
3.掌握指数函数图象及变换 直观想象
4.理解指数函数的单调性和特殊性 逻辑推理
情境与问题
考古学家经常利用碳 14 的含量来推断古生物死亡的大致时间. 当有机体生存时,会持续不断地吸收碳 14,从而其体内的碳 14 含量会保持在一定的水平 ; 但当有机体死亡后,就会停止吸收碳 14, 其体内的碳 14 含量就会逐渐减少,而且每经过大约 5730 年后会变为原来的一半 .
你能用函数表示有机体内的碳 14 含量与其死亡时间之间的关系吗? 一种死亡已经一万年的有机体 ,其体内的碳 14 含量是其生存时的百分之多少?
尝试与发现
指数函数
一般地,函数 y=ax 称为指数函数,其中 a 是常数,a>0 且 a≠1.
尝试与发现
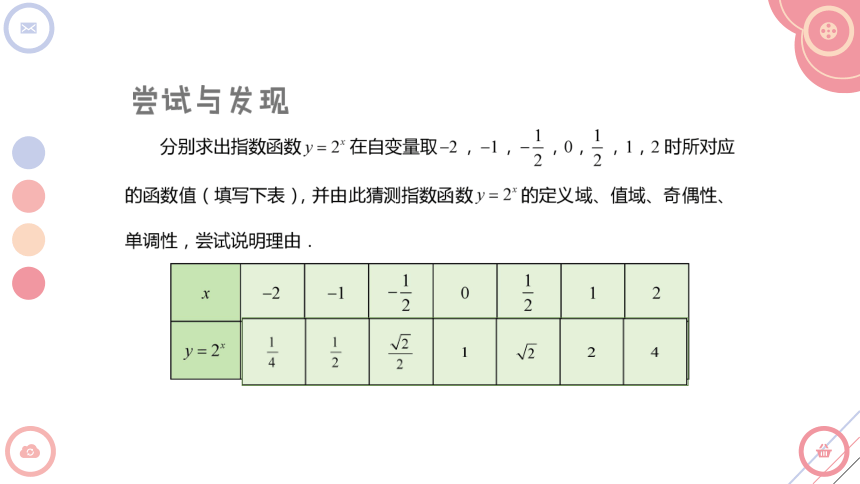
根据指数运算的定义,可以得到指数函数 y=2x 的性质:
(1)定义域是 ;
(2)值域是 ;
(3)奇偶性是 ;
(4)单调性是 .
R
(0,+∞)
非奇非偶函数
增函数
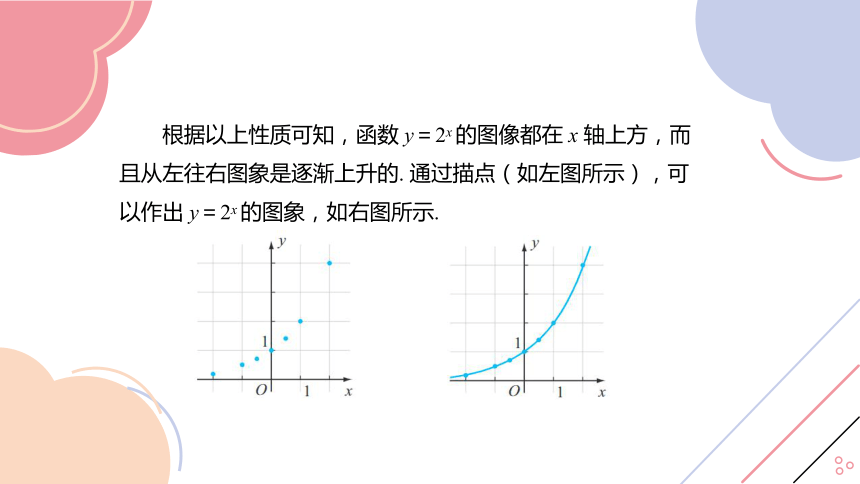
根据以上性质可知,函数 y=2x 的图像都在 x 轴上方,而且从左往右图象是逐渐上升的. 通过描点(如左图所示),可以作出 y=2x 的图象,如右图所示.
尝试与发现
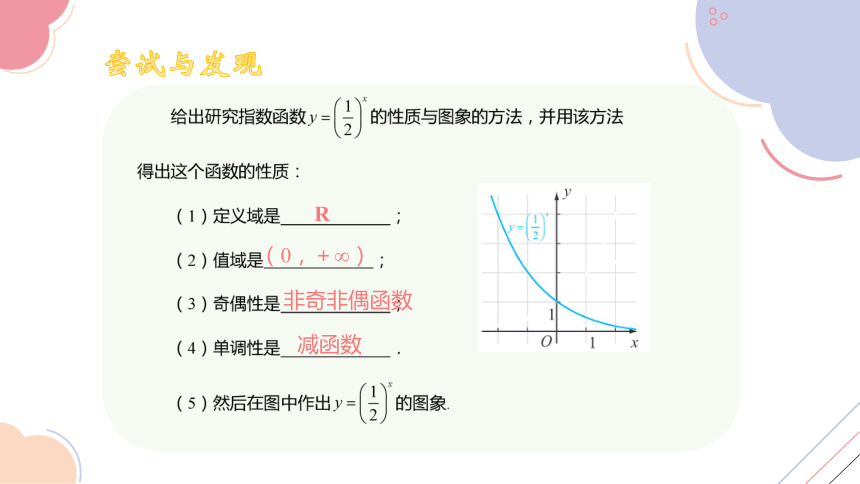
R
(0,+∞)
非奇非偶函数
减函数
尝试与发现
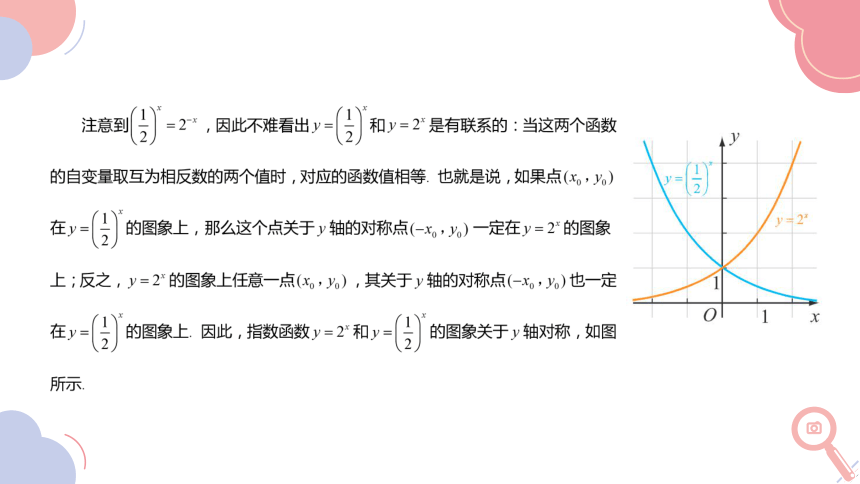
(1)你能指出指数函数 y=2x 和 y=的图象的公共点吗?
(2)你能得出指数函数 y=ax 一定过哪个定点吗?
函数 y=2x 和 y=的图象的公共点为 (0,1).
因为 a0=1 (a≠0),所以 y=ax 的图象一定过点 (0,1).
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
指数函数 y=ax (a>0且a ≠ 1)的性质
(1)定义域是实数集 R.
(2)值域是 (0 , +∞),因此,对任何实数 x,都有 ax>0,也就是说函数图象一定在 x 轴的上方.
(3)函数图象一定过点 (0 , 1).
(4)当 a>1 时,y=ax 是增函数;当0<a<1时,y=ax 是减函数.
分析:每一组的两个值都有共同特征,因此可以选取合适的函数,用函数的单调性来解决问题.
用信息技术作指数函数的图象
练习提升
C
D
D
C
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
A
C
A
B
BCD
ABD
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
1
或
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
1.指数函数的定义
2.指数函数的性质与图象
课堂小结:
本节课学习了哪些知识点呢?
感谢观看
第四章 指数函数、对数函数与幂函数
4.1.2 指数函数的性质与图象
人教B版(2019)
课标要点 核心素养
1.了解指数函数模型的实际背景 数学抽象
2.理解指数函数的概念及意义 直观想象
3.掌握指数函数图象及变换 直观想象
4.理解指数函数的单调性和特殊性 逻辑推理
情境与问题
考古学家经常利用碳 14 的含量来推断古生物死亡的大致时间. 当有机体生存时,会持续不断地吸收碳 14,从而其体内的碳 14 含量会保持在一定的水平 ; 但当有机体死亡后,就会停止吸收碳 14, 其体内的碳 14 含量就会逐渐减少,而且每经过大约 5730 年后会变为原来的一半 .
你能用函数表示有机体内的碳 14 含量与其死亡时间之间的关系吗? 一种死亡已经一万年的有机体 ,其体内的碳 14 含量是其生存时的百分之多少?
尝试与发现
指数函数
一般地,函数 y=ax 称为指数函数,其中 a 是常数,a>0 且 a≠1.
尝试与发现
根据指数运算的定义,可以得到指数函数 y=2x 的性质:
(1)定义域是 ;
(2)值域是 ;
(3)奇偶性是 ;
(4)单调性是 .
R
(0,+∞)
非奇非偶函数
增函数
根据以上性质可知,函数 y=2x 的图像都在 x 轴上方,而且从左往右图象是逐渐上升的. 通过描点(如左图所示),可以作出 y=2x 的图象,如右图所示.
尝试与发现
R
(0,+∞)
非奇非偶函数
减函数
尝试与发现
(1)你能指出指数函数 y=2x 和 y=的图象的公共点吗?
(2)你能得出指数函数 y=ax 一定过哪个定点吗?
函数 y=2x 和 y=的图象的公共点为 (0,1).
因为 a0=1 (a≠0),所以 y=ax 的图象一定过点 (0,1).
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
指数函数 y=ax (a>0且a ≠ 1)的性质
(1)定义域是实数集 R.
(2)值域是 (0 , +∞),因此,对任何实数 x,都有 ax>0,也就是说函数图象一定在 x 轴的上方.
(3)函数图象一定过点 (0 , 1).
(4)当 a>1 时,y=ax 是增函数;当0<a<1时,y=ax 是减函数.
分析:每一组的两个值都有共同特征,因此可以选取合适的函数,用函数的单调性来解决问题.
用信息技术作指数函数的图象
练习提升
C
D
D
C
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
A
C
A
B
BCD
ABD
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
1
或
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
●●●●●●●●●●●●●●●●●●●●●●●●●●●●●●
1.指数函数的定义
2.指数函数的性质与图象
课堂小结:
本节课学习了哪些知识点呢?
感谢观看
