4.2.1 对数运算 教学课件 (共29张PPT)- 高一数学人教B版(2019)必修第二册
文档属性
| 名称 | 4.2.1 对数运算 教学课件 (共29张PPT)- 高一数学人教B版(2019)必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-12 00:00:00 | ||
图片预览








文档简介
(共28张PPT)
4.2.1 对数运算
第四章
指数函数、对数函数与幂函数
人教B版(2019)
课标要点 核心素养
1.理解对数的概念 数学抽象
2.了解常用对数与自然对数 数学抽象
3.理解对数式与指数式的关系 数学运算
情境与问题
(1)地震的里氏震级是根据最大振幅计算出来的.2008 年 5 月 12 日,我国四川汶川发生了地震,速报震级为里氏 7.8 级,修订后的震级为里氏 8.0 级.震级相差 0.2,最大振幅之间具有什么关系?
(2)化学学科中,我们用 pH 表示溶液的酸碱性,pH是由 c(H+)(即溶液中 H+的浓度)决定的.pH=7 和 pH=8 的两种溶液,它们的 c(H+) 有什么关系?
在关系式 ab=N 中,以 a 或 N 为未知数的方程,我们都已经接触过,例如 x5=32,23=x 等,本节要研究 b 为未知数的情形,即求解类似 2x=64 的方程.
尝试与发现
(1)说出 2x=64 的一个实数根;
(2)判断方程 2x=64 的实数根的个数,并说明理由.
因为 26=64,所以 x=6 一定是 2x=64 的实数根,再由 y=2x 是一个增函数可知 2x=64 有唯一的实数解 x=6.
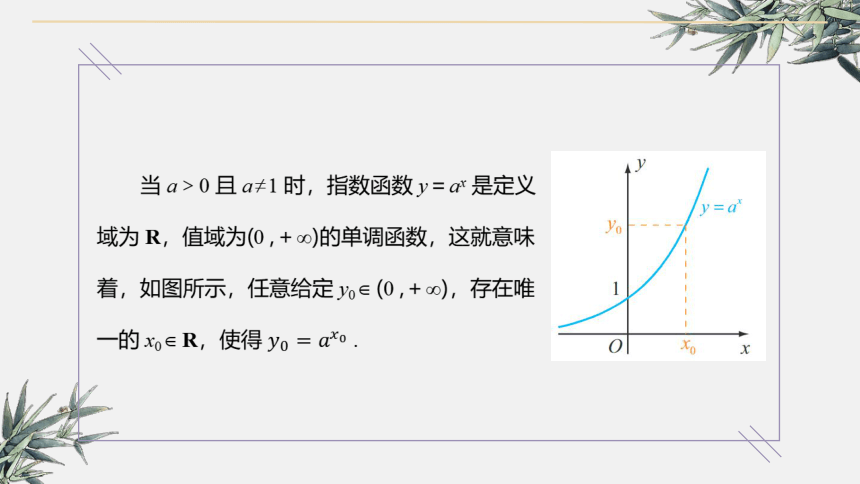
当 a>0 且 a≠1 时,指数函数 y=ax 是定义域为 R,值域为(0 ,+∞)的单调函数,这就意味着,如图所示,任意给定 y0 ∈ (0 ,+∞),存在唯一的 x0 ∈ R,使得 .
因此,在表达式 ab=N(a>0 且 a≠1,N ∈ (0 ,+∞))中,当 a与 N 确定之后,只有唯一的 b 能满足这个式子,此时,幂指数 b 称为以 a 为底 N 的对数,记作 b=logaN,其中 a 称为对数的底数,N称为对数的真数.
1.对数的概念
例如,由前面的尝试与发现可知,因为 26=64,所以 log264=6.
由上可以看出,当 a>0 且 a≠1 时,b=logaN 的充要条件是 ab=N.由此可知,只有 N>0 时,logaN 才有意义,这通常简称为“负数和零没有对数”.
因为 42=16,所以 2 是以 4 为底 16 的对数,即log416=2,即 42=16 log416=2,
另外, 41=4 log44=1,
可以举出更多对数的例子:
例1 已知 a>0 且 a≠1,求 loga1 与 logaa 的值.
解:因为 a0=1,a1=a,所以 loga1=0,logaa=1.
例1的结论可以简述为“1的对数为0”
“底的对数为1”.
由上可知,指数表达式 ab=N 与对数表达式 b=logaN 实际上表示的是同一数量关系,如果把对数表达式中的 b 代入指数表达式,则可得 alogaN=N ;类似地,如果把指数表达式中的 N 代入对数表达式,则有____________.
例如,2log232=______,log10103=_______.
logaab=b
32
3
例2 求下列各式的值:
(1)log216; (2) ; (3)52log53
解:(1)因为24=16,所以log216=4.
(2)因为2-1= ,所以 log2 =-1.
(3)因为 5log53=3,所以 52log53=(5log53)2=32=9.
2.常用对数与自然对数
以 10 为底的对数称为常用对数,即 log10N 是常用对数.为了简便起见,常用对数的表示中,通常把底 10 略去不写,并把“log”写成“lg”,即把 log10N 简写为 lgN.
后续如果没有指出对数的底,则默认为指的都是常用对数.例如,“100 的对数是 2”,就是指“100 的常用对数是 2”.
在科学技术中,常常还使用以无理数 e=2.718 28…为底的对数,以 e 为底的对数称为自然对数,自然对数 logeN 通常简写为 ln N.
例3 求下列各式的值:
(1)lg 10; (2)lg 100; (3)lg 0.01; (4)ln e5.
解:(1)因为101=10,所以 lg10=1;
(2)因为102=100,所以 lg100= ;
(3)因为10-2=0.01,所以 1g 0.01= ;
(4)因为 logaab=b,所以 ln e5= .
2
-2
5
例4 已知 log4a=log25b=,求 lg(ab) 的值.
用信息技术计算常用对数与自然对数
常用对数与自然对数的值,可以通过科学计算器和计算机软件求得.
图(1)是某特定型号计算器上的常用对数按钮和自然对数按钮,
图(2)显示的是用 GeoGerra 计算 lg2 017 和 ln2 017 的结果
练习提升
C
B
B
D
BD
0
-3
课堂小结:
本节课学习了哪些知识点呢?
1.对数的概念
2.常用对数与自然对数
感谢观看
4.2.1 对数运算
第四章
指数函数、对数函数与幂函数
人教B版(2019)
课标要点 核心素养
1.理解对数的概念 数学抽象
2.了解常用对数与自然对数 数学抽象
3.理解对数式与指数式的关系 数学运算
情境与问题
(1)地震的里氏震级是根据最大振幅计算出来的.2008 年 5 月 12 日,我国四川汶川发生了地震,速报震级为里氏 7.8 级,修订后的震级为里氏 8.0 级.震级相差 0.2,最大振幅之间具有什么关系?
(2)化学学科中,我们用 pH 表示溶液的酸碱性,pH是由 c(H+)(即溶液中 H+的浓度)决定的.pH=7 和 pH=8 的两种溶液,它们的 c(H+) 有什么关系?
在关系式 ab=N 中,以 a 或 N 为未知数的方程,我们都已经接触过,例如 x5=32,23=x 等,本节要研究 b 为未知数的情形,即求解类似 2x=64 的方程.
尝试与发现
(1)说出 2x=64 的一个实数根;
(2)判断方程 2x=64 的实数根的个数,并说明理由.
因为 26=64,所以 x=6 一定是 2x=64 的实数根,再由 y=2x 是一个增函数可知 2x=64 有唯一的实数解 x=6.
当 a>0 且 a≠1 时,指数函数 y=ax 是定义域为 R,值域为(0 ,+∞)的单调函数,这就意味着,如图所示,任意给定 y0 ∈ (0 ,+∞),存在唯一的 x0 ∈ R,使得 .
因此,在表达式 ab=N(a>0 且 a≠1,N ∈ (0 ,+∞))中,当 a与 N 确定之后,只有唯一的 b 能满足这个式子,此时,幂指数 b 称为以 a 为底 N 的对数,记作 b=logaN,其中 a 称为对数的底数,N称为对数的真数.
1.对数的概念
例如,由前面的尝试与发现可知,因为 26=64,所以 log264=6.
由上可以看出,当 a>0 且 a≠1 时,b=logaN 的充要条件是 ab=N.由此可知,只有 N>0 时,logaN 才有意义,这通常简称为“负数和零没有对数”.
因为 42=16,所以 2 是以 4 为底 16 的对数,即log416=2,即 42=16 log416=2,
另外, 41=4 log44=1,
可以举出更多对数的例子:
例1 已知 a>0 且 a≠1,求 loga1 与 logaa 的值.
解:因为 a0=1,a1=a,所以 loga1=0,logaa=1.
例1的结论可以简述为“1的对数为0”
“底的对数为1”.
由上可知,指数表达式 ab=N 与对数表达式 b=logaN 实际上表示的是同一数量关系,如果把对数表达式中的 b 代入指数表达式,则可得 alogaN=N ;类似地,如果把指数表达式中的 N 代入对数表达式,则有____________.
例如,2log232=______,log10103=_______.
logaab=b
32
3
例2 求下列各式的值:
(1)log216; (2) ; (3)52log53
解:(1)因为24=16,所以log216=4.
(2)因为2-1= ,所以 log2 =-1.
(3)因为 5log53=3,所以 52log53=(5log53)2=32=9.
2.常用对数与自然对数
以 10 为底的对数称为常用对数,即 log10N 是常用对数.为了简便起见,常用对数的表示中,通常把底 10 略去不写,并把“log”写成“lg”,即把 log10N 简写为 lgN.
后续如果没有指出对数的底,则默认为指的都是常用对数.例如,“100 的对数是 2”,就是指“100 的常用对数是 2”.
在科学技术中,常常还使用以无理数 e=2.718 28…为底的对数,以 e 为底的对数称为自然对数,自然对数 logeN 通常简写为 ln N.
例3 求下列各式的值:
(1)lg 10; (2)lg 100; (3)lg 0.01; (4)ln e5.
解:(1)因为101=10,所以 lg10=1;
(2)因为102=100,所以 lg100= ;
(3)因为10-2=0.01,所以 1g 0.01= ;
(4)因为 logaab=b,所以 ln e5= .
2
-2
5
例4 已知 log4a=log25b=,求 lg(ab) 的值.
用信息技术计算常用对数与自然对数
常用对数与自然对数的值,可以通过科学计算器和计算机软件求得.
图(1)是某特定型号计算器上的常用对数按钮和自然对数按钮,
图(2)显示的是用 GeoGerra 计算 lg2 017 和 ln2 017 的结果
练习提升
C
B
B
D
BD
0
-3
课堂小结:
本节课学习了哪些知识点呢?
1.对数的概念
2.常用对数与自然对数
感谢观看
