4.2.3 对数函数的性质与图象 教学课件(共41张PPT) - 高一数学人教B版(2019)必修第二册
文档属性
| 名称 | 4.2.3 对数函数的性质与图象 教学课件(共41张PPT) - 高一数学人教B版(2019)必修第二册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-12 21:42:44 | ||
图片预览








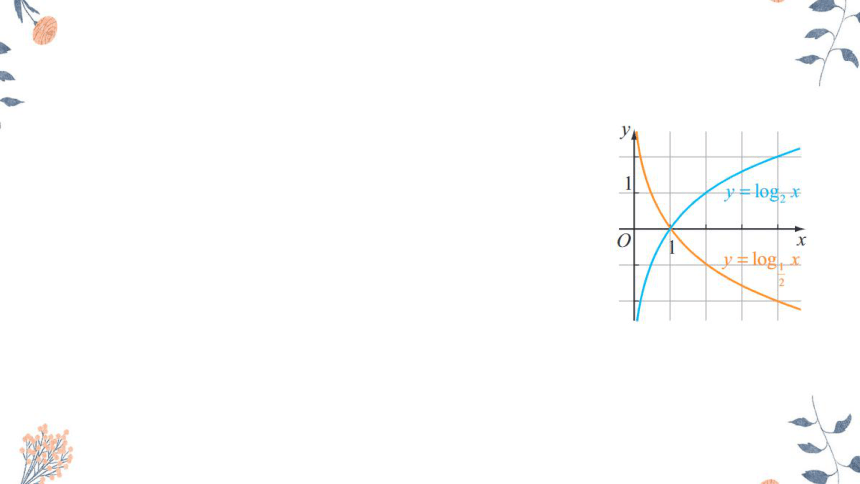

文档简介
(共40张PPT)
4.2.3 对数函数的性质与图象
第四章
指数函数、对数函数与幂函数
人教B版(2019)
课标要点 核心素养
1.理解对数函数的概念 数学抽象
2.了解对数函数图象及变换 直观想象
3.理解对数函数的单调性 逻辑推理
情境与问题
我们已经知道,假设有机体生存时碳 14 的含量为 1,那么有机体死亡 x 年后内体内碳 14 的含量 y 满足,也就是说,y 是 x 的函数.
在得到古生物的样品时,考古学家能够测量出其中的碳 14 含量 y,你认为考社学家们能利用这个值推断出古生物的死亡时间 x 吗?给定一个 y 值,有多少个 x 值与之对应?这里的 x 能看成 y 的函数吗?为什么?
对数函数
一般地,函数 y=loga x 称为对数函数,其中 a 是常数,a>0且a≠1.
尝试与发现
-3
-2
-1
0
1
2
3
可以看出,y=log2x 中,x 不能是-1,也不能是 0.
事实上,根据对数运算的定义和性质,可以得到对数函数 y=log2x 的性质:
(1)定义域是 ;
(2)值域是 ;
(3)奇偶性是 ;
(4)单调性是 .
(0 , +∞ )
R
非奇非偶函数
增函数
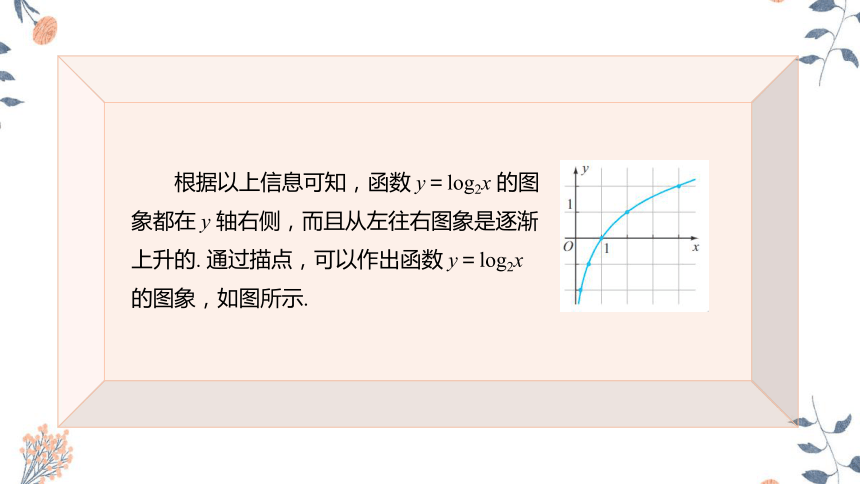
根据以上信息可知,函数 y=log2x 的图象都在 y 轴右侧,而且从左往右图象是逐渐上升的. 通过描点,可以作出函数 y=log2x 的图象,如图所示.
(1)你能指出对数函数 y=log2x 和 y=x 的图象的公共点吗?这两个函数图象的关系如何?
(2)你能得出指数函数 y=logax 一定过哪个定点吗?
尝试与发现
函数 y=log2x 和 y=x 的图象的公共点为(1,0).
因为 loga1=0,所以 y=logax 的图象一定过点(1,0).
对数函数 y=logax 的性质
(1)定义域是(0,+∞),因此函数图象一定在 y 轴的右边.
(2)值域是实数集 R.
(3)函数图象一定过点(1,0).
(4)当 a>1时,y=logax 是增函数;当0用信息技术作对数函数的图象
练习提升
C
C
A
A
D
C
C
D
ABC
-2
1.对数函数的概念
2.对数函数的性质与图象
课堂小结:
本节课学习了哪些知识点呢?
谢谢观看
4.2.3 对数函数的性质与图象
第四章
指数函数、对数函数与幂函数
人教B版(2019)
课标要点 核心素养
1.理解对数函数的概念 数学抽象
2.了解对数函数图象及变换 直观想象
3.理解对数函数的单调性 逻辑推理
情境与问题
我们已经知道,假设有机体生存时碳 14 的含量为 1,那么有机体死亡 x 年后内体内碳 14 的含量 y 满足,也就是说,y 是 x 的函数.
在得到古生物的样品时,考古学家能够测量出其中的碳 14 含量 y,你认为考社学家们能利用这个值推断出古生物的死亡时间 x 吗?给定一个 y 值,有多少个 x 值与之对应?这里的 x 能看成 y 的函数吗?为什么?
对数函数
一般地,函数 y=loga x 称为对数函数,其中 a 是常数,a>0且a≠1.
尝试与发现
-3
-2
-1
0
1
2
3
可以看出,y=log2x 中,x 不能是-1,也不能是 0.
事实上,根据对数运算的定义和性质,可以得到对数函数 y=log2x 的性质:
(1)定义域是 ;
(2)值域是 ;
(3)奇偶性是 ;
(4)单调性是 .
(0 , +∞ )
R
非奇非偶函数
增函数
根据以上信息可知,函数 y=log2x 的图象都在 y 轴右侧,而且从左往右图象是逐渐上升的. 通过描点,可以作出函数 y=log2x 的图象,如图所示.
(1)你能指出对数函数 y=log2x 和 y=x 的图象的公共点吗?这两个函数图象的关系如何?
(2)你能得出指数函数 y=logax 一定过哪个定点吗?
尝试与发现
函数 y=log2x 和 y=x 的图象的公共点为(1,0).
因为 loga1=0,所以 y=logax 的图象一定过点(1,0).
对数函数 y=logax 的性质
(1)定义域是(0,+∞),因此函数图象一定在 y 轴的右边.
(2)值域是实数集 R.
(3)函数图象一定过点(1,0).
(4)当 a>1时,y=logax 是增函数;当0
练习提升
C
C
A
A
D
C
C
D
ABC
-2
1.对数函数的概念
2.对数函数的性质与图象
课堂小结:
本节课学习了哪些知识点呢?
谢谢观看
