4.3 指数函数与对数函数的关系 课件(共37张PPT) - 高一数学人教B版(2019)必修第二册
文档属性
| 名称 | 4.3 指数函数与对数函数的关系 课件(共37张PPT) - 高一数学人教B版(2019)必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-12 00:00:00 | ||
图片预览










文档简介
(共36张PPT)
第四章
指数函数、对数函数与幂函数
4.3 指数函数与对数函数的关系
人教B版(2019)
课标要点 核心素养
1.掌握指数函数与对数函数的关系 逻辑推理
2.理解反函数的概念 数学抽象
3.了解求反函数的步骤 逻辑推理
指数函数与对数函数的性质可列表如下:
函数 指数函数 y=ax 对数函数 y=loga x
定义域
值域
单调性 0<a<1时,为________;a>1时,为_________
R
(0 ,+∞)
减函数
增函数
(0 ,+∞)
R
由此可以看出,指数函数 y=ax 与对数函数 y=loga x 中,一个函数的定义域是另一个函数的值域,而且它们的单调性相同. 这是因为在上述两个函数中,通过对调其中一个函数的自变量和因变量,可得到另一个函数.
一般地,如果在函数 y=f (x) 中,给定值域中任意一个 y 的值,只有唯一的 x 与之对应,那么 x 是 y 的函数,这个函数称为 y=f (x) 的反函数.此时,称 y=f (x) 存在反函数.
反函数
如果函数的自变量仍用 x 表示,因变量仍用 y 表示,则函数 y=f (x) 的反函数的表达式,可以通过对调 y=f (x) 中的 x 与 y,然后从 x=f (y) 中求出 y 得到.
例如,y=2x 是增函数,因此任意给定一个 y 值,只有唯一的 x 与之对应,所以 y=2x 存在反函数. 对调 y=2x 中的 x 和 y 得 x=2y,解得 y=log2x . 因此 y=log2x 是 y=2x 的反函数.
如图是同一平面直角坐标系内函数 y=2x 以及它的反函数 y=log2x 的图象,不难看出,它们的图象关于直线 y=x 对称.
一般地,函数 y=f (x) 的反函数记作 y=f-1 (x) .值得注意的是,y=f (x) 的定义域与y=f-1 (x) 的值域相同,y=f (x) 的值域与 y=f-1 (x) 的定义域相同,y=f (x) 与 y=f-1 (x) 的图象关于直线 y=x 对称.
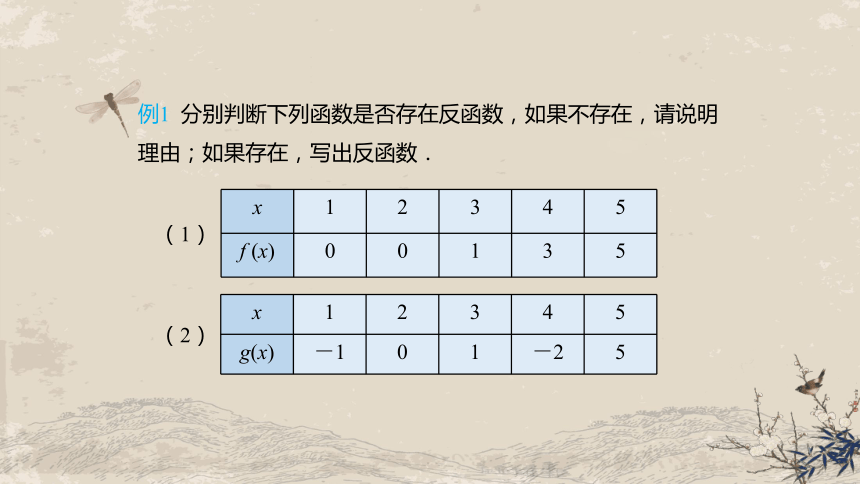
例1 分别判断下列函数是否存在反函数,如果不存在,请说明理由;如果存在,写出反函数.
(1)
x 1 2 3 4 5
f (x) 0 0 1 3 5
(2)
x 1 2 3 4 5
g(x) -1 0 1 -2 5
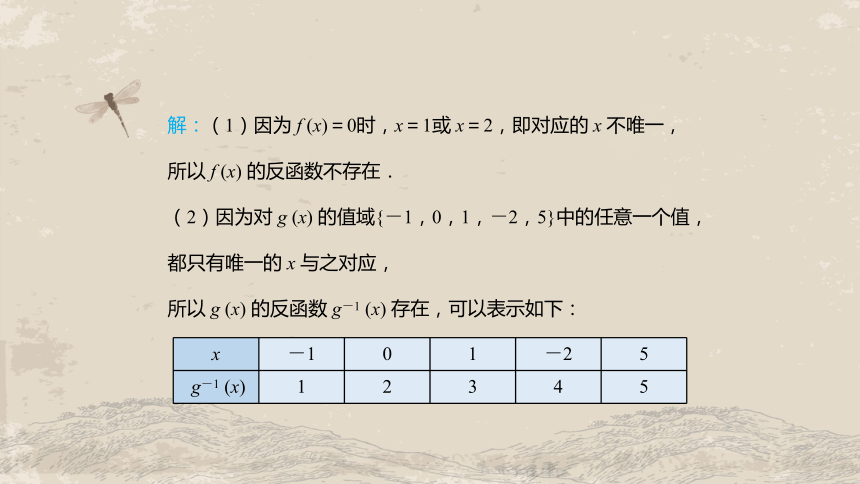
解:(1)因为 f (x)=0时,x=1或 x=2,即对应的 x 不唯一,
所以 f (x) 的反函数不存在.
(2)因为对 g (x) 的值域{-1,0,1,-2,5}中的任意一个值,都只有唯一的 x 与之对应,
所以 g (x) 的反函数 g-1 (x) 存在,可以表示如下:
x -1 0 1 -2 5
g-1 (x) 1 2 3 4 5
例2 判断 f (x)=2x+2 的反函数是否存在,如果不存在,说明理由;如果存在,写出反函数 f-1 (x) 的解析式,并在同一平面直角坐标系中作出 f (x) 与 f-1 (x) 的函数图象.
练习提升
A
B
A
D
A
C
B
A
C
-3
12
(2 , 1)
1.指数函数与对数函数的关系
2.反函数
课堂小结:
本节课学习了哪些知识点呢?
谢观看
感
第四章
指数函数、对数函数与幂函数
4.3 指数函数与对数函数的关系
人教B版(2019)
课标要点 核心素养
1.掌握指数函数与对数函数的关系 逻辑推理
2.理解反函数的概念 数学抽象
3.了解求反函数的步骤 逻辑推理
指数函数与对数函数的性质可列表如下:
函数 指数函数 y=ax 对数函数 y=loga x
定义域
值域
单调性 0<a<1时,为________;a>1时,为_________
R
(0 ,+∞)
减函数
增函数
(0 ,+∞)
R
由此可以看出,指数函数 y=ax 与对数函数 y=loga x 中,一个函数的定义域是另一个函数的值域,而且它们的单调性相同. 这是因为在上述两个函数中,通过对调其中一个函数的自变量和因变量,可得到另一个函数.
一般地,如果在函数 y=f (x) 中,给定值域中任意一个 y 的值,只有唯一的 x 与之对应,那么 x 是 y 的函数,这个函数称为 y=f (x) 的反函数.此时,称 y=f (x) 存在反函数.
反函数
如果函数的自变量仍用 x 表示,因变量仍用 y 表示,则函数 y=f (x) 的反函数的表达式,可以通过对调 y=f (x) 中的 x 与 y,然后从 x=f (y) 中求出 y 得到.
例如,y=2x 是增函数,因此任意给定一个 y 值,只有唯一的 x 与之对应,所以 y=2x 存在反函数. 对调 y=2x 中的 x 和 y 得 x=2y,解得 y=log2x . 因此 y=log2x 是 y=2x 的反函数.
如图是同一平面直角坐标系内函数 y=2x 以及它的反函数 y=log2x 的图象,不难看出,它们的图象关于直线 y=x 对称.
一般地,函数 y=f (x) 的反函数记作 y=f-1 (x) .值得注意的是,y=f (x) 的定义域与y=f-1 (x) 的值域相同,y=f (x) 的值域与 y=f-1 (x) 的定义域相同,y=f (x) 与 y=f-1 (x) 的图象关于直线 y=x 对称.
例1 分别判断下列函数是否存在反函数,如果不存在,请说明理由;如果存在,写出反函数.
(1)
x 1 2 3 4 5
f (x) 0 0 1 3 5
(2)
x 1 2 3 4 5
g(x) -1 0 1 -2 5
解:(1)因为 f (x)=0时,x=1或 x=2,即对应的 x 不唯一,
所以 f (x) 的反函数不存在.
(2)因为对 g (x) 的值域{-1,0,1,-2,5}中的任意一个值,都只有唯一的 x 与之对应,
所以 g (x) 的反函数 g-1 (x) 存在,可以表示如下:
x -1 0 1 -2 5
g-1 (x) 1 2 3 4 5
例2 判断 f (x)=2x+2 的反函数是否存在,如果不存在,说明理由;如果存在,写出反函数 f-1 (x) 的解析式,并在同一平面直角坐标系中作出 f (x) 与 f-1 (x) 的函数图象.
练习提升
A
B
A
D
A
C
B
A
C
-3
12
(2 , 1)
1.指数函数与对数函数的关系
2.反函数
课堂小结:
本节课学习了哪些知识点呢?
谢观看
感
