4.4 幂函数 教学课件(共43张PPT) - 高一数学人教B版(2019)必修第二册
文档属性
| 名称 | 4.4 幂函数 教学课件(共43张PPT) - 高一数学人教B版(2019)必修第二册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-12 00:00:00 | ||
图片预览











文档简介
(共42张PPT)
第四章 指数函数、对数函数与幂函数
4.4 幂函数
人教B版(2019)
课标要点 核心素养
1.了解幂函数的概念 数学抽象
2.了解五个常见幂函数的图象 直观想象
3.了解幂函数的图象与性质 逻辑推理
情境与问题
我们已经知道,在关系式 N=ab 中,当底数 a 为大于 0 且不等于 1 的常数时;如果把 b 作为自变量、N 作为因变量,则 N 就是 b 的指数函数;如果把 N 作为自变量、b 作为因变量,则 b 就是 N 的对数函数(即 b=logaN ).那么,当 b 为常数时,是否可以将底数 a 作为自变量,N 作为因变量来构造函数关系呢?
在关系式 N=ab 中,以 a 为自变量、N 为因变量构造出来的函数 y=xb 就是本节要讨论的幂函数.
尝试与发现
我们以前学过函数 y=x,y=x2,y=,这三个函数的解析式有什么共同的特点吗?你能根据指数运算的定义,把这三个函数的解析式改写成统一的形式吗?
一般地,函数 y=xα 称为幂函数,其中 α 为常数.
幂函数
上面提到的函数 y=x,y=x2,y=都是幂函数.
尝试与发现
判断-4,-3,-2,-1,,0,,1,2,3,4 这些数中,哪些在函数 的定义域内,求出对应的函数值,并填写下表(只需要填在定义域内的数及对应的函数值),由此猜测这个函数的定义域、值域、奇偶性、单调性,尝试并说明理由.
x
0
0
0
0
0
0
1
2
由于 ,由此不难知道,函数 的性质有:
(1)定义域是___________;
(2)值域是___________;
(3)奇偶性是_____________;
(4)单调性是___________.
[0,+∞)
非奇非偶函数
增函数
[0,+∞)
根据以上信息可知,函数 的图象上的点,除了原点,其余点都在第一象限,通过描点(如左图所示),可作出其图象,如右图所示
尝试与发现
给出研究函数 y=x3 的性质与图象的方法,并用你的方法得出这个函数的性质:
(1)定义域是___________;
(2)值域是___________;
(3)奇偶性是___________;
(4)单调性是___________;
R
R
奇函数
增函数
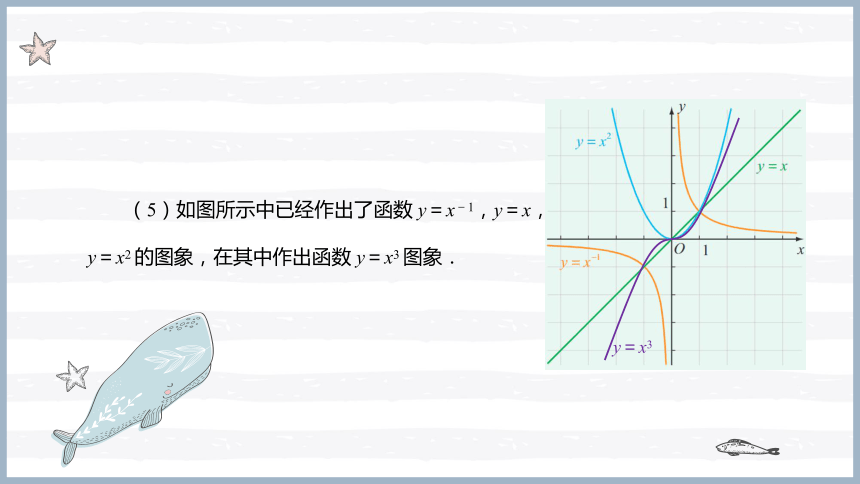
(5)如图所示中已经作出了函数 y=x-1,y=x,y=x2 的图象,在其中作出函数 y=x3 图象.
y=x3
一般地,幂函数 y=xα,随着 α 的取值不同,函数的定义域、值域、奇偶性、单调性也不尽相同,但也有一些共同的特征:
(1)所有的幂函数在区间(0 , +∞)上都有定义,因此在第一象限内都有图象,并且图象都通过点(1 , 1).
(2)如果 α>0,则幂函数的图象通过原点,并且在区间 [0 , +∞)上是增函数.
(3)如果 α<0,则幂函数在区间(0 , +∞)上是减函数,且在第一象限内:当 x 从右边趋向于原点时,图象在 y 轴右方且无限地通近 y 轴;当 x 无限增大时,图象在 x 轴上方且无限地逼近 x 轴.
例2 讨论函数 的定义域、奇偶性,通过描点作出它的图象,并根据图象说明函数的单调性.
用信息技术作幂函数的图象
练习提升
A
D
C
B
C
C
B
AC
CD
(,4)
1.幂函数的概念
2.幂函数的性质与图象
课堂小结:
本节课学习了哪些知识点呢?
感谢观看
Bye~
第四章 指数函数、对数函数与幂函数
4.4 幂函数
人教B版(2019)
课标要点 核心素养
1.了解幂函数的概念 数学抽象
2.了解五个常见幂函数的图象 直观想象
3.了解幂函数的图象与性质 逻辑推理
情境与问题
我们已经知道,在关系式 N=ab 中,当底数 a 为大于 0 且不等于 1 的常数时;如果把 b 作为自变量、N 作为因变量,则 N 就是 b 的指数函数;如果把 N 作为自变量、b 作为因变量,则 b 就是 N 的对数函数(即 b=logaN ).那么,当 b 为常数时,是否可以将底数 a 作为自变量,N 作为因变量来构造函数关系呢?
在关系式 N=ab 中,以 a 为自变量、N 为因变量构造出来的函数 y=xb 就是本节要讨论的幂函数.
尝试与发现
我们以前学过函数 y=x,y=x2,y=,这三个函数的解析式有什么共同的特点吗?你能根据指数运算的定义,把这三个函数的解析式改写成统一的形式吗?
一般地,函数 y=xα 称为幂函数,其中 α 为常数.
幂函数
上面提到的函数 y=x,y=x2,y=都是幂函数.
尝试与发现
判断-4,-3,-2,-1,,0,,1,2,3,4 这些数中,哪些在函数 的定义域内,求出对应的函数值,并填写下表(只需要填在定义域内的数及对应的函数值),由此猜测这个函数的定义域、值域、奇偶性、单调性,尝试并说明理由.
x
0
0
0
0
0
0
1
2
由于 ,由此不难知道,函数 的性质有:
(1)定义域是___________;
(2)值域是___________;
(3)奇偶性是_____________;
(4)单调性是___________.
[0,+∞)
非奇非偶函数
增函数
[0,+∞)
根据以上信息可知,函数 的图象上的点,除了原点,其余点都在第一象限,通过描点(如左图所示),可作出其图象,如右图所示
尝试与发现
给出研究函数 y=x3 的性质与图象的方法,并用你的方法得出这个函数的性质:
(1)定义域是___________;
(2)值域是___________;
(3)奇偶性是___________;
(4)单调性是___________;
R
R
奇函数
增函数
(5)如图所示中已经作出了函数 y=x-1,y=x,y=x2 的图象,在其中作出函数 y=x3 图象.
y=x3
一般地,幂函数 y=xα,随着 α 的取值不同,函数的定义域、值域、奇偶性、单调性也不尽相同,但也有一些共同的特征:
(1)所有的幂函数在区间(0 , +∞)上都有定义,因此在第一象限内都有图象,并且图象都通过点(1 , 1).
(2)如果 α>0,则幂函数的图象通过原点,并且在区间 [0 , +∞)上是增函数.
(3)如果 α<0,则幂函数在区间(0 , +∞)上是减函数,且在第一象限内:当 x 从右边趋向于原点时,图象在 y 轴右方且无限地通近 y 轴;当 x 无限增大时,图象在 x 轴上方且无限地逼近 x 轴.
例2 讨论函数 的定义域、奇偶性,通过描点作出它的图象,并根据图象说明函数的单调性.
用信息技术作幂函数的图象
练习提升
A
D
C
B
C
C
B
AC
CD
(,4)
1.幂函数的概念
2.幂函数的性质与图象
课堂小结:
本节课学习了哪些知识点呢?
感谢观看
Bye~
