3.1.1 椭圆及其标准方程 课件(共37页PPT) ——高二数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 3.1.1 椭圆及其标准方程 课件(共37页PPT) ——高二数学人教A版(2019)选择性必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-12 21:46:54 | ||
图片预览





文档简介
(共36张PPT)
3.1.1 椭圆及其标准方程
学习目标
掌握椭圆的定义、标准方程
通过对椭圆标准方程的推导,进一步体会数形几何的思想
学习重点
学习难点
椭圆的标准方程,坐标法的基本思想
椭圆的标准方程的推掉与化简,坐标法的应用
新课导入
椭圆是圆锥曲线的一种,具有丰富的几何性质,在科研、生产和人类生活中具有广泛的应用. 那么,椭圆到底有怎样的几何特征?我们该如何利用这些特征建立椭圆的方程,从而为研究椭圆的几何性质奠定基础?
新课学习
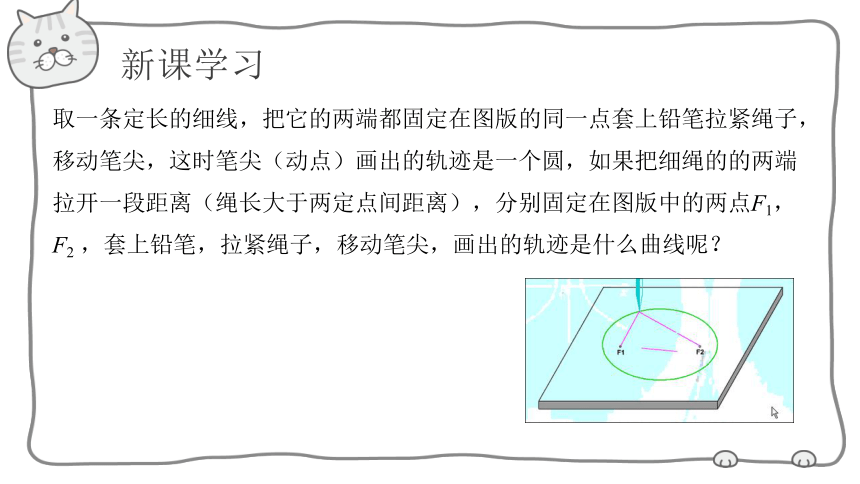
取一条定长的细线,把它的两端都固定在图版的同一点套上铅笔拉紧绳子,移动笔尖,这时笔尖(动点)画出的轨迹是一个圆,如果把细绳的的两端拉开一段距离(绳长大于两定点间距离),分别固定在图版中的两点F1,F2 ,套上铅笔,拉紧绳子,移动笔尖,画出的轨迹是什么曲线呢?
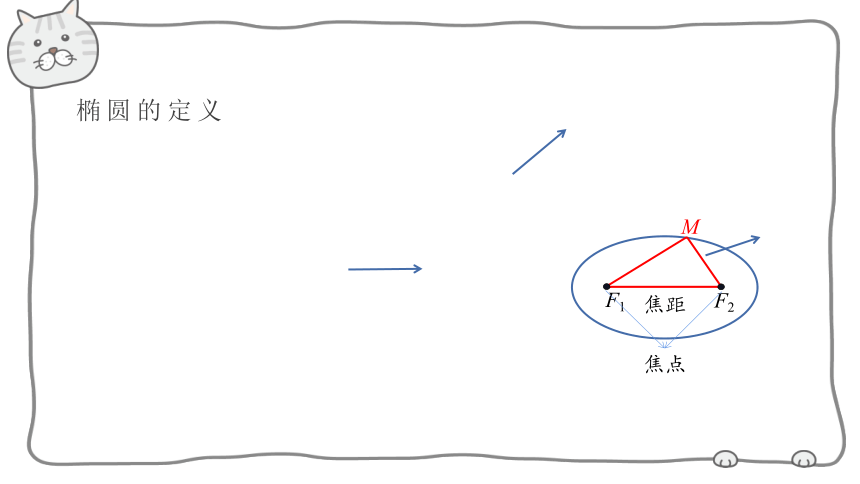
椭圆的定义
F1
F2
焦距
焦点
M
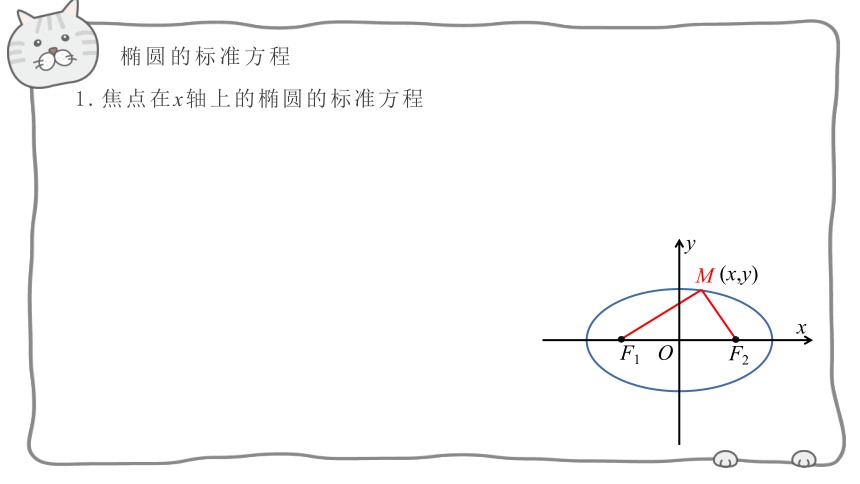
椭圆的标准方程
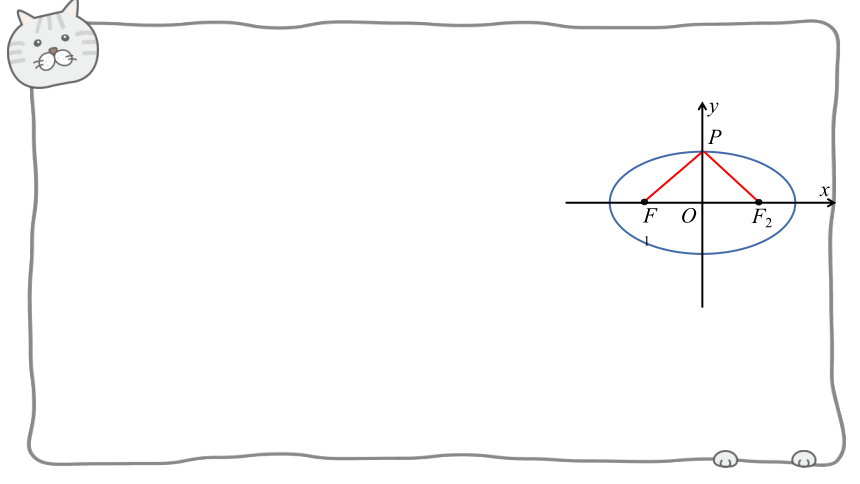
1.焦点在x轴上的椭圆的标准方程
F1
F2
M
x
O
y
(x,y)
1.焦点在x轴上的椭圆的标准方程
F1
F2
P
x
O
y
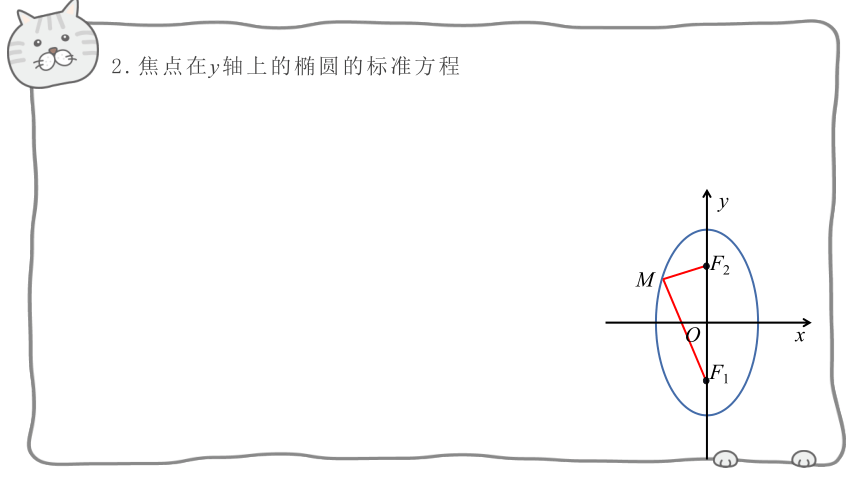
2.焦点在y轴上的椭圆的标准方程
F1
F2
M
x
O
y
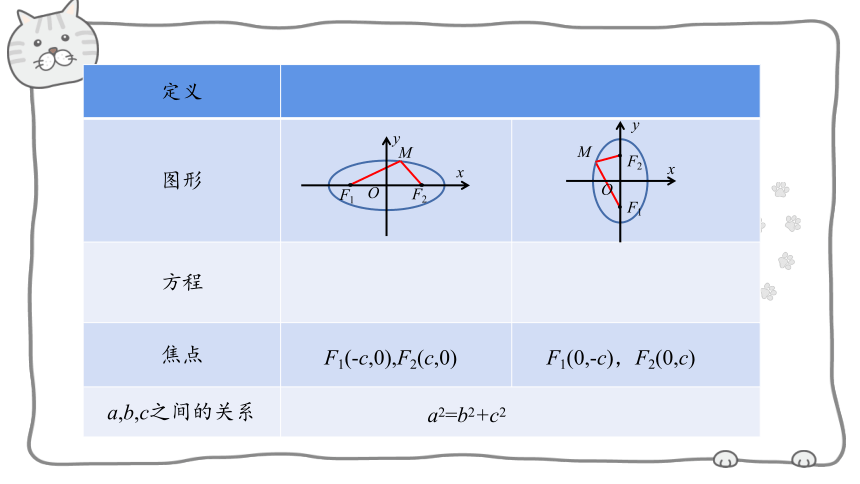
定义
图形
方程
焦点
a,b,c之间的关系
F1
F2
M
x
O
y
F1
F2
M
x
O
y
F1(-c,0),F2(c,0)
F1(0,-c),F2(0,c)
a2=b2+c2
例题来了
解:
解:
求椭圆标准方程的步骤:
1.“定位” 即确定椭圆的焦点在哪条坐标轴上;
2.“定量”即确定 的具体数值.
3.求椭圆标准方程的常用方法:待定系数法及定义法.
解:
定义法求椭圆的标准方法(与椭圆有关的轨迹方程)的两种思路
(1)首先通过题干中给出的等量关系列出等式,然后化简等式得到对应的轨迹方程.
(2)首先分析几何图形所表示的几何关系,然后对比椭圆的定义,设出对应椭圆的方程,求a,b的值,得到标准方程.
共焦点的椭圆系方程
课堂巩固
B
A
D
C
A
总结一下
1.椭圆的定义
2.椭圆的标准方程
感谢你们的聆听观看!
Lorem ipsum dolor sit amet, please add your text here, lorem ipsum dolor sit amet, please add your text here , lorem ipsum dolor sit amet, please add your text here , lorem ipsum dolor sit amet, please add your text here。
3.1.1 椭圆及其标准方程
学习目标
掌握椭圆的定义、标准方程
通过对椭圆标准方程的推导,进一步体会数形几何的思想
学习重点
学习难点
椭圆的标准方程,坐标法的基本思想
椭圆的标准方程的推掉与化简,坐标法的应用
新课导入
椭圆是圆锥曲线的一种,具有丰富的几何性质,在科研、生产和人类生活中具有广泛的应用. 那么,椭圆到底有怎样的几何特征?我们该如何利用这些特征建立椭圆的方程,从而为研究椭圆的几何性质奠定基础?
新课学习
取一条定长的细线,把它的两端都固定在图版的同一点套上铅笔拉紧绳子,移动笔尖,这时笔尖(动点)画出的轨迹是一个圆,如果把细绳的的两端拉开一段距离(绳长大于两定点间距离),分别固定在图版中的两点F1,F2 ,套上铅笔,拉紧绳子,移动笔尖,画出的轨迹是什么曲线呢?
椭圆的定义
F1
F2
焦距
焦点
M
椭圆的标准方程
1.焦点在x轴上的椭圆的标准方程
F1
F2
M
x
O
y
(x,y)
1.焦点在x轴上的椭圆的标准方程
F1
F2
P
x
O
y
2.焦点在y轴上的椭圆的标准方程
F1
F2
M
x
O
y
定义
图形
方程
焦点
a,b,c之间的关系
F1
F2
M
x
O
y
F1
F2
M
x
O
y
F1(-c,0),F2(c,0)
F1(0,-c),F2(0,c)
a2=b2+c2
例题来了
解:
解:
求椭圆标准方程的步骤:
1.“定位” 即确定椭圆的焦点在哪条坐标轴上;
2.“定量”即确定 的具体数值.
3.求椭圆标准方程的常用方法:待定系数法及定义法.
解:
定义法求椭圆的标准方法(与椭圆有关的轨迹方程)的两种思路
(1)首先通过题干中给出的等量关系列出等式,然后化简等式得到对应的轨迹方程.
(2)首先分析几何图形所表示的几何关系,然后对比椭圆的定义,设出对应椭圆的方程,求a,b的值,得到标准方程.
共焦点的椭圆系方程
课堂巩固
B
A
D
C
A
总结一下
1.椭圆的定义
2.椭圆的标准方程
感谢你们的聆听观看!
Lorem ipsum dolor sit amet, please add your text here, lorem ipsum dolor sit amet, please add your text here , lorem ipsum dolor sit amet, please add your text here , lorem ipsum dolor sit amet, please add your text here。
