8.4 机械能守恒定律 课件-2024-2025学年高一下学期物理人教版(2019)必修第二册(共16张PPT)
文档属性
| 名称 | 8.4 机械能守恒定律 课件-2024-2025学年高一下学期物理人教版(2019)必修第二册(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 47.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-07-13 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
第八章:机械能守恒定律
8.4 机械能守恒定律
学习目标
1、通过机械能守恒定律的学习,初步建立能量观念、体会守恒思想。
2、会用能量观念分析具体实例中动能与势能(包括弹性势能)之间的相互转化。
3、理解机械能守恒定律的推导过程。
4、会从做功和能量转化的角度判断机械能是否守恒,能应用机械能守恒定律解决有关问题,体会利用机械能守恒定律解决问题的便利性。
√
课堂引入
讨论这些情境中动能和势能的转化。
一、动能与势能的相互转化
伽利略理想斜面实验
思考:在小球的运动过程中,有哪些物理量是变化的?哪些是不变的?你能找出不变的量吗?
重力势能、弹性势能与动能都是机械运动中的能量形式,统称为机械能。
二、机械能守恒定律
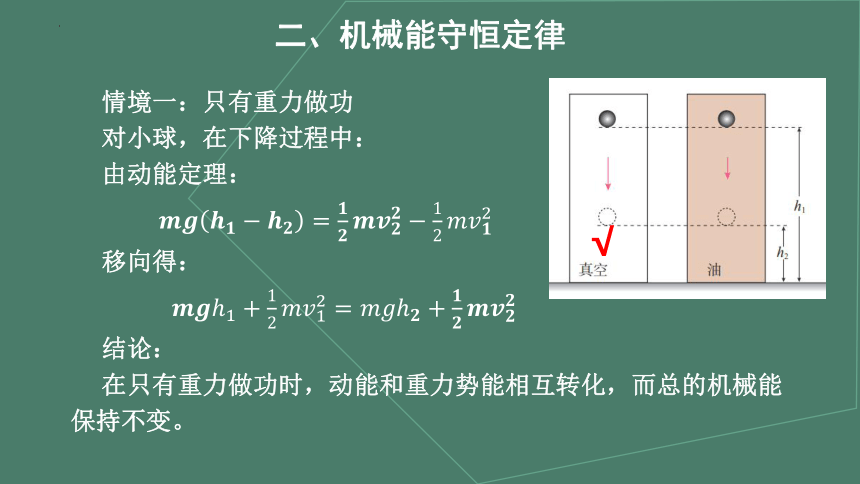
情境一:只有重力做功
对小球,在下降过程中:
由动能定理:
移向得:
结论:
在只有重力做功时,动能和重力势能相互转化,而总的机械能保持不变。
√
二、机械能守恒定律
情境二:只有弹簧弹力做功
对小球,在运动过程中:
由动能定理:
由功能关系:
联立得:
移向得:
结论:在只有弹簧弹力做功的小球和弹簧系统内,动能和弹性势能相互转化,而系统的总机械能保持不变。
压缩的弹簧
v1=0
弹簧恢复原来形状
v2=6m/s
v1=6m/s
v2=0
二、机械能守恒定律
情境三:还有其他力做功
对小球,在下降过程中:
由动能定理:
移向得:
结论:有摩擦阻力做功时,机械能会改变。
结论:摩擦阻力做的功,等于机械能的改变量。
√
二、机械能守恒定律
1、内容:在只有重力或弹力做功的物体系统内,动能与势能可以相互转化,而总的机械能保持不变。这叫做机械能守恒定律。
2、机械能守恒的条件:只有重力或系统内的弹力做功。
3、表达式:常用表达式有三种
(1)
注意:选用此式解题时,需选取零势能面。
(2) ΔEk增=ΔEp减 (或 ΔEp增=ΔEk减)
(3) ΔEA增=ΔEB减 (或ΔEB增=ΔEA减)
4、机械能守恒的常见类型:
(1)物体只受重力或系统内弹力作用;
(2)物体除受重力或系统内弹力外,还受其他力,但其他力不做功;
(3)物体还受其他力,其他力做功,但其他力做功的代数和为0.
注:若其他力做功的代数和不为0,则机械
三、机械能守恒的判断
机械能守恒的判断方法
1、做功条件分析法:应用机械能守恒的条件进行判断。分析物体(或系统)的受力情况(包括内力和外力),明确各力做功的情况,若只有重力或弹力做功,没有其他力做功或其他力做功的代数和为零,则物体(或系统)的机械能守恒。
2、能量转化分析法:从能量转化的角度进行判断。若只有系统内物体间动能和重力势能及弹性势能的相互转化,机械能也没有转化成其他形式的能(如内能),则系统的机械能守恒。
3、增减情况分析法:直接从各种形式机械能的增减情况进行判断。如系统的动能不变,势能增加,则系统的机械能不守恒。
练习1、在下面列举的各个实例中(除 A 外都不计空气阻力),哪些过程中机械能是守恒的?说明理由。
A.跳伞运动员带着张开的降落伞在空中匀速下落
B.抛出的标枪在空中运动
C.拉着一个金属块使它沿光滑的斜面匀速上升
D.在光滑水平面上运动的小球碰到一个弹簧,把弹簧压缩后,又被弹回来
√
√
练习2、(多选)如图,小球自a点由静止自由下落,到b点时与弹簧接触,到c点时弹簧被压缩到最短,若不计弹簧质量和空气阻力,在小球由b→c的运动过程中,下列说法正确的是( )
A.小球和弹簧构成的系统总机械能守恒
B.小球的重力势能随时间先减少后增加
C.小球在b点时动能最大
D.小球动能的减少量小于弹簧弹性势能的增加量
√
√
四、机械能守恒定律的应用
(一)单个物体的机械能守恒
课本93页,练习与应用T3
对石块在下落过程中,以地面为零势能面,由机械能守恒定律可得:
代入可解得:
对石块在下落过程中,由动能定理可得:
代入可解得:
m=0.5kg
v0=5m/s
h=10m
g=10m/s2
对于单体问题,动能定理和机械能守恒定律解题均比较方便。
四、机械能守恒定律的应用
(二)多个物体的机械能守恒
课本93页,练习与应用T4
分析:对A、B组成的系统,除重力外,拉力对A做正功、对B做负功,且拉力做功的代数和为0.
解:设A的质量为 m,B的质量为 3m,B落地时A的速度为 v。
对A、B组成的系统,在B下落 h、A上升h的过程中,以地面为参考系,由机械能守恒定律得:
解得:
A的质量是B的三倍
对于多体问题,机械能守恒定律解决问题更加方便。
四、机械能守恒定律的应用
总结:应用机械能守恒定律解决问题的基本思路:
练习3、如图所示,质量不计的轻杆一端安装在水平轴O上,杆的中央和另一端分别固定一个质量均为m的小球A和B,杆长为l,将轻杆在水平位置由静止开始释放,不计空气阻力。当轻杆通过竖直位置时,问:小球A、B的速度大小各是多少?
答案:
练习4、有一条长为L=2 m的均匀金属链条,有一半长度在光滑的足够高的斜面上,斜面顶端是一个很小的圆弧,斜面倾角为30°,另一半长度竖直下垂在空中,当链条从静止开始释放后链条滑动,则链条刚好全部滑出斜面时的速度为(g取10 m/s2)( )
A.2.5 m/s B. m/s C.m/s D. m/s
√
课堂小结
一、机械能守恒定律
机械能:重力势能、弹性势能与动能统称为机械能。
1、内容:在只有重力或弹力做功的物体系统内,动能与势能可以相互转化,而总的机械能保持不变。这叫做机械能守恒定律。
2、机械能守恒的条件:只有重力或系统内的弹力做功。
3、表达式:常用表达式有三种
(1)
注意:选用此式解题时,需选取零势能面。
(2) ΔEk增=ΔEp减 (或 ΔEp增=ΔEk减)
(3) ΔEA增=ΔEB减 (或ΔEB增=ΔEA减)
4、机械能守恒的常见类型:
(1)物体只受重力或系统内弹力作用;
(2)物体除受重力或系统内弹力外,还受其他力,但其他力不做功;
(3)物体还受其他力,其他力做功,但其他力做功的代数和为0.
注:若其他力做功的代数和不为0,则机械
课堂小结
二、机械能守恒的判断
1、做功条件分析法:若只有重力或弹力做功,没有其他力做功或其他力做功的代数和为零,则物体(或系统)的机械能守恒。
2、能量转化分析法:若只有系统内物体间动能和重力势能及弹性势能的相互转化,机械能没有转化成其他形式的能(如内能),则系统的机械能守恒。
3、增减情况分析法:直接从各种形式机械能的增减情况进行判断。如系统的动能不变,势能增加,则系统的机械能不守恒。
三、机械能守恒定律的应用
1、对于单体问题,动能定理和机械能守恒定律解题均比较方便。
2、对于多体问题,机械能守恒定律解决问题更加方便。
3、解题基本思路:
练习与应用T5
第八章:机械能守恒定律
8.4 机械能守恒定律
学习目标
1、通过机械能守恒定律的学习,初步建立能量观念、体会守恒思想。
2、会用能量观念分析具体实例中动能与势能(包括弹性势能)之间的相互转化。
3、理解机械能守恒定律的推导过程。
4、会从做功和能量转化的角度判断机械能是否守恒,能应用机械能守恒定律解决有关问题,体会利用机械能守恒定律解决问题的便利性。
√
课堂引入
讨论这些情境中动能和势能的转化。
一、动能与势能的相互转化
伽利略理想斜面实验
思考:在小球的运动过程中,有哪些物理量是变化的?哪些是不变的?你能找出不变的量吗?
重力势能、弹性势能与动能都是机械运动中的能量形式,统称为机械能。
二、机械能守恒定律
情境一:只有重力做功
对小球,在下降过程中:
由动能定理:
移向得:
结论:
在只有重力做功时,动能和重力势能相互转化,而总的机械能保持不变。
√
二、机械能守恒定律
情境二:只有弹簧弹力做功
对小球,在运动过程中:
由动能定理:
由功能关系:
联立得:
移向得:
结论:在只有弹簧弹力做功的小球和弹簧系统内,动能和弹性势能相互转化,而系统的总机械能保持不变。
压缩的弹簧
v1=0
弹簧恢复原来形状
v2=6m/s
v1=6m/s
v2=0
二、机械能守恒定律
情境三:还有其他力做功
对小球,在下降过程中:
由动能定理:
移向得:
结论:有摩擦阻力做功时,机械能会改变。
结论:摩擦阻力做的功,等于机械能的改变量。
√
二、机械能守恒定律
1、内容:在只有重力或弹力做功的物体系统内,动能与势能可以相互转化,而总的机械能保持不变。这叫做机械能守恒定律。
2、机械能守恒的条件:只有重力或系统内的弹力做功。
3、表达式:常用表达式有三种
(1)
注意:选用此式解题时,需选取零势能面。
(2) ΔEk增=ΔEp减 (或 ΔEp增=ΔEk减)
(3) ΔEA增=ΔEB减 (或ΔEB增=ΔEA减)
4、机械能守恒的常见类型:
(1)物体只受重力或系统内弹力作用;
(2)物体除受重力或系统内弹力外,还受其他力,但其他力不做功;
(3)物体还受其他力,其他力做功,但其他力做功的代数和为0.
注:若其他力做功的代数和不为0,则机械
三、机械能守恒的判断
机械能守恒的判断方法
1、做功条件分析法:应用机械能守恒的条件进行判断。分析物体(或系统)的受力情况(包括内力和外力),明确各力做功的情况,若只有重力或弹力做功,没有其他力做功或其他力做功的代数和为零,则物体(或系统)的机械能守恒。
2、能量转化分析法:从能量转化的角度进行判断。若只有系统内物体间动能和重力势能及弹性势能的相互转化,机械能也没有转化成其他形式的能(如内能),则系统的机械能守恒。
3、增减情况分析法:直接从各种形式机械能的增减情况进行判断。如系统的动能不变,势能增加,则系统的机械能不守恒。
练习1、在下面列举的各个实例中(除 A 外都不计空气阻力),哪些过程中机械能是守恒的?说明理由。
A.跳伞运动员带着张开的降落伞在空中匀速下落
B.抛出的标枪在空中运动
C.拉着一个金属块使它沿光滑的斜面匀速上升
D.在光滑水平面上运动的小球碰到一个弹簧,把弹簧压缩后,又被弹回来
√
√
练习2、(多选)如图,小球自a点由静止自由下落,到b点时与弹簧接触,到c点时弹簧被压缩到最短,若不计弹簧质量和空气阻力,在小球由b→c的运动过程中,下列说法正确的是( )
A.小球和弹簧构成的系统总机械能守恒
B.小球的重力势能随时间先减少后增加
C.小球在b点时动能最大
D.小球动能的减少量小于弹簧弹性势能的增加量
√
√
四、机械能守恒定律的应用
(一)单个物体的机械能守恒
课本93页,练习与应用T3
对石块在下落过程中,以地面为零势能面,由机械能守恒定律可得:
代入可解得:
对石块在下落过程中,由动能定理可得:
代入可解得:
m=0.5kg
v0=5m/s
h=10m
g=10m/s2
对于单体问题,动能定理和机械能守恒定律解题均比较方便。
四、机械能守恒定律的应用
(二)多个物体的机械能守恒
课本93页,练习与应用T4
分析:对A、B组成的系统,除重力外,拉力对A做正功、对B做负功,且拉力做功的代数和为0.
解:设A的质量为 m,B的质量为 3m,B落地时A的速度为 v。
对A、B组成的系统,在B下落 h、A上升h的过程中,以地面为参考系,由机械能守恒定律得:
解得:
A的质量是B的三倍
对于多体问题,机械能守恒定律解决问题更加方便。
四、机械能守恒定律的应用
总结:应用机械能守恒定律解决问题的基本思路:
练习3、如图所示,质量不计的轻杆一端安装在水平轴O上,杆的中央和另一端分别固定一个质量均为m的小球A和B,杆长为l,将轻杆在水平位置由静止开始释放,不计空气阻力。当轻杆通过竖直位置时,问:小球A、B的速度大小各是多少?
答案:
练习4、有一条长为L=2 m的均匀金属链条,有一半长度在光滑的足够高的斜面上,斜面顶端是一个很小的圆弧,斜面倾角为30°,另一半长度竖直下垂在空中,当链条从静止开始释放后链条滑动,则链条刚好全部滑出斜面时的速度为(g取10 m/s2)( )
A.2.5 m/s B. m/s C.m/s D. m/s
√
课堂小结
一、机械能守恒定律
机械能:重力势能、弹性势能与动能统称为机械能。
1、内容:在只有重力或弹力做功的物体系统内,动能与势能可以相互转化,而总的机械能保持不变。这叫做机械能守恒定律。
2、机械能守恒的条件:只有重力或系统内的弹力做功。
3、表达式:常用表达式有三种
(1)
注意:选用此式解题时,需选取零势能面。
(2) ΔEk增=ΔEp减 (或 ΔEp增=ΔEk减)
(3) ΔEA增=ΔEB减 (或ΔEB增=ΔEA减)
4、机械能守恒的常见类型:
(1)物体只受重力或系统内弹力作用;
(2)物体除受重力或系统内弹力外,还受其他力,但其他力不做功;
(3)物体还受其他力,其他力做功,但其他力做功的代数和为0.
注:若其他力做功的代数和不为0,则机械
课堂小结
二、机械能守恒的判断
1、做功条件分析法:若只有重力或弹力做功,没有其他力做功或其他力做功的代数和为零,则物体(或系统)的机械能守恒。
2、能量转化分析法:若只有系统内物体间动能和重力势能及弹性势能的相互转化,机械能没有转化成其他形式的能(如内能),则系统的机械能守恒。
3、增减情况分析法:直接从各种形式机械能的增减情况进行判断。如系统的动能不变,势能增加,则系统的机械能不守恒。
三、机械能守恒定律的应用
1、对于单体问题,动能定理和机械能守恒定律解题均比较方便。
2、对于多体问题,机械能守恒定律解决问题更加方便。
3、解题基本思路:
练习与应用T5
