北师大版八年级数学上册试题 第6章 数据的分析 章节测试卷(含解析)
文档属性
| 名称 | 北师大版八年级数学上册试题 第6章 数据的分析 章节测试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 367.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-13 09:23:13 | ||
图片预览




文档简介
第6章《数据的分析》章节测试卷
、
一.选择题(共10小题,满分30分,每小题3分)
1.八(1)班的学生从第一学期到第二学期时,下列有关年龄的统计量不变的是( )
A.平均年龄 B.年龄的方差 C.年龄的众数 D.年龄的中位数
2.小明家至月份的用水量统计如图所示,关于这组数据,下列说法中错误的是( )
A.众数是 吨 B.平均数是 吨 C.中位数是 吨 D.方差是吨
3.某校八年级学生参加每分钟跳绳的测试,并随机抽取部分学生的成绩制成了频数分布直方图(如图),若取每组的组中值作为本小组的均值,则抽取的部分学生每分钟跳绳次数的平均值(结果取整数)为( )
A.87次 B.110次 C.112次 D.120次
4.如图所示的扇形统计图描述了某校学生对课后延时服务的打分情况(满分5分),则所打分数的众数是( )
A.3分 B.3.55分 C.4分 D.
5.八位评委对参加演讲比赛的选手评分,比赛规则规定要去掉一个最高分和一个最低分,然后计算剩下的6个分数的平均分作为选手的比赛得分,规则“去掉一个最高分和一个最低分”一定不会影响这组数据的( )
A.平均数 B.中位数 C.极差 D.众数
6.育新中学八年级六班有53人.一次月考后,数学老师对数学成绩进行了统计.由于有三人因事没有参加本次月考,因此计算其他50人的平均分为90分,方差.后来三进行了补考,数学成绩分别为88分,90分,92分.加入这三人的成绩后,下列说法正确的是( )
A.平均分和方差都改变 B.平均分不变,方差变大
C.平均分不变,方差变小 D.平均分和方差都不变
7.一组数据的方差为,将这组数据中每个数据都除以3,所得新数据的方差是( )
A. B.3 C. D.9
8.(3分)某同学各科成绩如图所示,则其成绩的中位数是( )
A.75分 B.75.5分 C.76分 D.77分
9.第组数据为:,第组数据为:、,其中是正整数.下列结论:
①当时,两组数据的平均数相等;
②当时,第组数据的平均数小于第组数据的平均数;
③当时,第组数据的中位数小于第组数据的中位数;
④当时,第组数据的方差小于第组数据的方差.
其中正确的是( )
A.①② B.②③ C.①③ D.②④
10.某数学兴趣小组对我县祁禄山的红军小道的长度进行次测量,得到个结果,,,…,(单位:).如果用作为这条路线长度的近似值,要使得的值最小,应选取这次测量结果的( )
A.中位数 B.众数 C.平均数 D.最小值
二.填空题(共6小题,满分18分,每小题3分)
11.某学校开展“齐诵满江红,传承报国志”诵读比赛,八年级准备从小乐和小涵两位同学中选拔一位同学参加决赛,如图是小乐和小涵两位同学参加5次选拔赛的测试成绩(满分为100分)折线统计图,若选择一位成绩优异且稳定的同学参赛,推选参加决赛的同学是 (填“小乐”或“小涵”).
12.有一组数据:.将这组数据改变为.设这组数据改变前后的方差分别是,则与的大小关系是 .
13.两组数据:3,a,2b,5与a,6,b的平均数都是6,若将这两组数据合并为一组数据,则这组新数据的众数为 .
14.甲、乙、丙三种糖果的售价分别为每千克6元、每千克7元、每千克8元,若将甲种糖果6千克,乙种糖果10千克,丙种糖果4千克混合在一起,则混合后的糖果的售价应定为每千克 元.
15.若质数a,b满足,则数据a,b,2,3的中位数是 .
16.若五个整数由小到大排列后,中位数为4,唯一的众数为2,则这组数据之和的最小值是 .
三.解答题(共7小题,满分52分)
17.(6分)已知一组数据:x,10,12,6的中位数与平均数相等,求x的值.
18.(6分)校园广播站招聘小记者,对应聘同学分别进行笔试(含阅读能力、思维能力和表达能力三项测试)和面试,应聘者小成同学成绩单位:分如下表:
笔试 面试
成绩 阅读能力 思维能力 表达能力 92
88 90 86
(1)请求出小成同学的笔试平均成绩;
(2)如果笔试平均成绩与面试成绩按的比例确定总成绩,请求出小成同学的总成绩.
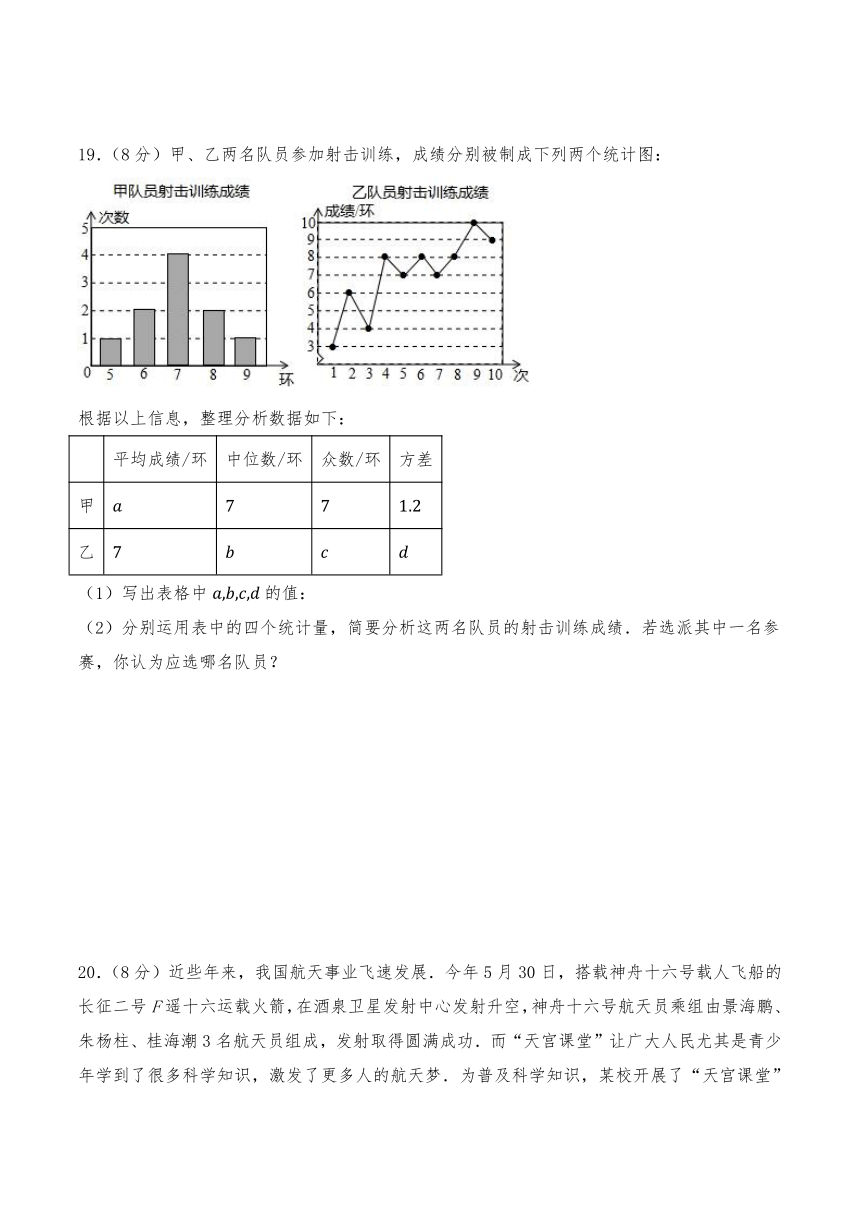
19.(8分)甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
根据以上信息,整理分析数据如下:
平均成绩/环 中位数/环 众数/环 方差
甲
乙
(1)写出表格中的值:
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
20.(8分)近些年来,我国航天事业飞速发展.今年5月30日,搭载神舟十六号载人飞船的长征二号F遥十六运载火箭,在酒泉卫星发射中心发射升空,神舟十六号航天员乘组由景海鹏、朱杨柱、桂海潮3名航天员组成,发射取得圆满成功.而“天宫课堂”让广大人民尤其是青少年学到了很多科学知识,激发了更多人的航天梦.为普及科学知识,某校开展了“天宫课堂”知识竞赛.为了解七、八年级学生(八年级有600名学生、八年级有800名学生)的竞赛情况,现从两个年级各随机抽取20名学生的成绩(百分制)进行分析.过程如下:
【收集数据】八年级20名学生成绩:62,52,58,67,70,69,75,73,75,75,80,78,77,90,81,84,86,88,94,98;
八年级20名学生成绩在的分数:83,85,87,81,80,84,82;
【整理数据】按照分数段,整理、描述两组样本数据:
年级
八年级 5 a 5 3
八年级 3 6 7 4
【分析数据】两组样本数据的平均数、中位数、众数、方差如表所示:
年级 平均数 中位数 众数 方差
八年级 76.6 76 b 131
八年级 76.6 c 78 124
(1)直接写出a、b、c的值;
(2)根据抽样调查数据,估计全校七、八年级“天宫课堂”竞赛成绩为优秀(80分及以上)的共有多少人?
【得出结论】
(3)通过以上分析,你认为这两个年级中哪个年级对“天宫课堂”知识掌握情况更好一些,并说明推断的合理性(写出一条理由即可).
21.(8分)每年4月中上旬的体育考试,是初三同学们决胜中考的第一关,为了解我校初届学生的体育训练情况,对初届学生进行了一次体育机器模拟测试.测试完成后,在初届的学生中随机抽取了名男生,名女生的本次体育机考的测试成绩,对数据进行整理分析,并给出了下列信息:
①名女生的测试成绩统计如下:,,,,,,,,,,,,,,,,,,,.
②抽取的名男生的测试成绩扇形统计图如图:
③抽取的名男生成绩得分用表示,共分成五组::;:;:;:;:.其中,抽取的名男生的测试成绩中,组的成绩如下:,,,,,.
④抽取男生与女生的学生的测试成绩的平均数、中位数、众数如表所示:
性别 平均数 中位数 众数
女生
男生
(1)根据以上信息可以求出:______,______,______;
(2)结合以上的数据分析,针对本次的体育测试成绩中,你认为此次的体育测试成绩男生与女生谁更好?请说明理由(理由写出一条即可);
(3)若初届学生中男生有人,女生有人,(规定分及以上为优秀)请估计该校初届参加此次体育测试的学生中成绩为优秀的学生人数.
22.(8分)某校为了解八年级800名学生跳绳情况,从八年级学生中随机抽取50名学生进行1分钟跳绳测试,并对测试成绩进行统计,绘制了如下统计表.
组别 1分钟跳绳个数 频数 组内学生平均1分钟跳绳个数
6 80
15 120
20 145
9 180
其中组同学跳绳个数:
130,134,135,136,138,140,142,142,143,144,
145,145,147,148,150,152,155,157,158,159.
根据以上信息,回答下列问题:
(1)这50名学生1分钟跳绳个数的中位数是_______;
(2)求这50名学生1分钟跳绳个数的平均数;
(3)若跳绳个数超过140个为优秀,则该校八年级学生跳绳成绩优秀的约有多少人?
23.(8分)甲、乙两名队员练习射击,每次射击的环数为整数,两人各射击10次,其成绩分别绘制成如图1、图2所示的统计图,两幅图均有部分被污染,两名队员10次的射击成绩整理后,得到的统计表如下表所示.
平均数 中位数 众数 方差
甲 a 7 b 1.8
乙 7 c 8 3
(1)甲队员射中7环的次数为___________;
(2)统计表中___________;___________;___________;
(3)___________队员的发挥更稳定;
(4)乙队员补射1次后,成绩为m环,据统计乙队员这11次射击成绩的中位数比c大0.5,则m的最小值为___________.
答案与试题
选择题
1.B
【分析】根据当数据都加上一个数时的平均数、方差、众数、中位数的变化特征逐项判断即可解答.
【详解】解:由题意知,八年级一班的学生升八年级时,每个同学的年龄都加1,
其中平均年龄加1,众数加1,中位数加1,方差不变,
故A、C、D不符合要求;B符合要求.
故选:B.
2.C
【分析】根据众数、平均数、中位数和方差的定义计算各量,然后对各选项进行判断.
【详解】∵这组数据的6出现了3次,3,4,5各出现了1次,
∴众数为6吨,
∵平均数为吨,方差为吨,中位数是吨,
∴A,B,D选项正确,不符合题意,C选项错误,符合题意,
故选:C
3.C
【分析】根据众数的定义求解即可
【详解】解:∵,
∴由扇形统计图知,得4分的人数占总人数的,人数最多,
所以所打分数的众数为4分,
故选:C.
5.B
【分析】根据平均数、中位数、众数、极差的意义分别判断即可得到答案.
【详解】去掉一个最高分和一个最低分后一定会影响平均分、极差,有可能影响众数,但是这组数据的中间两个数没有变化故一定不会影响中位数,
故选:B.
6.C
【分析】分别求出加入三人成绩后的平均分、方差,然后比较大小即可.
【详解】解:由题意知,加入三人成绩后的平均分为:,
∴平均分不变,
方差为:,
∵,
∴方差变小,
故选:C.
7.C
【分析】本题主要考查的是方差的求法.解答此类问题,通常用x1,x2,…,xn表示出已知数据的平均数与方差,再根据题意用x1,x2,…,xn表示出新数据的平均数与方差,寻找新数据的平均数与原来数据平均数之间的关系.
【详解】设原数据为x1,x2,…,xn,其平均数为,方差为s2.根据题意,得新数据为,,…,,其平均数为.根据方差的定义可知,新数据的方差为.故选C.
【点睛】本题考查平均数与方差,会分别利用方差和平均数的公式去表示方差和平均数是解题的关键.其次根据题意给代数式进行等量变形也非常重要.
8.(3分)(2023春·江西九江·八年级统考期中)某同学各科成绩如图所示,则其成绩的中位数是( )
9.C
【分析】根据平均数的定义,中位数的定义,方差的定义对每一项判断解答即可.
【详解】解:∵第组数据为:,
∴第组数据的平均数为,
∵第组数据为:、,
∴第组数据平均数为,
∵,
∴第组数据平均数,
∴当时,两组数据的平均数相等,
故①正确;
∵当时,,
∴第组数据平均数,
∴第组数据的平均数大于第组数据的平均数,
故②错误;
∵第组数据为:,
∴第组数据的中位数为,
∵第组数据为:、,
∴当时,若为奇数时,第组数据的中位数为;若偶数,第组数据的中位数是为,
∴当时,第组的中位数为,
当时,第组数据的中位数小于第组数据的中位数,
故③正确;
∵第组数据为:,
∴第组数据方差:,
∵第组数据为:、,
∴第组数据的方差为,
∴当时,第组数据的方差等于第组数据的方差,
∴正确的序号为①③,
故选.
10.C
【分析】先设出y=(x﹣x1)2+(x﹣x2)2+(x﹣x3)2+…+(x﹣xn)2,然后进行整理得出y=nx2﹣2(x1+x2+x3+…+xn)x+(x12+x22+x32+…+xn2),再求出二次函数的最小值,再根据x的取值即可得出答案.
【详解】解:设y=(x﹣x1)2+(x﹣x2)2+(x﹣x3)2+…+(x﹣xn)2
y=x2﹣2xx1+x12+x2﹣2xx2+x22+x2﹣2xx3+x32+…+x2﹣2xxn+xn2
y=nx2﹣2(x1+x2+x3+…+xn)x+(x12+x22+x32+…+xn2),
则当x=时,
二次函数y=nx2﹣2(x1+x2+x3+…+xn)x+(x12+x22+x32+…+xn2)最小,
∴x所取平均数时,结果最小,
故选:C.
二.填空题
11.解:根据题意得:
,
,
,
,
,
小涵的成绩优异且稳定,
推选参加决赛的同学是小涵,
故答案为:小涵.
12.
【分析】设数据,,,,的平均数为,根据平均数的定义得出数据,,,,的平均数也为,再利用方差的定义分别求出,,进而比较大小.
【详解】解:设数据,,,,的平均数为,则数据,,,,的平均数也为,
,
,
.
故答案为.
13.8
【分析】根据平均数的意义,求出a、b的值,进而确定两组数据,再合并成一组,找出出现次数最多的数据即可.
【详解】解:由题意得,
,
解得,
这两组数合并成一组新数据为:,
在这组新数据中,出现次数最多的是8,因此众数是8,
故答案为:8.
14.6.9
【分析】先根据甲种糖果6千克,乙种糖果10千克,丙种糖果4千克求出混合后的糖果甲、乙、丙比,再用各自所占比乘各自的售货单价相加即可.
【详解】解:若将甲种糖果6千克,乙种糖果10千克,丙种糖果4千克混合在一起,
则混合后的糖果甲、乙、丙比为,
∴混合后的糖果的售价每千克应定为(元),
故答案为:6.9.
15.4或7
【分析】由题意知,即,且a,b是质数,可得或或或,解方程组可得满足要求的的值,然后根据中位数是第二、三位数的平均数求解即可.
【详解】解:由题意知,即,且a,b是质数,
∴或或或,
解得,,(舍去),(舍去),
当时,2,3,5,7的中位数为;
当时,2,3,11,13的中位数为;
∴数据a,b,2,3的中位数是4或7,
故答案为:4或7.
16.19
【分析】根据“五个整数由小到大排列后,中位数为4,唯一的众数为2”,可知此组数据的第三个数是4,第一个和第二个数是2,据此可知当第四个数是5,第五个数是6时和最小.
【详解】∵中位数为4
∴中间的数为4,
又∵众数是2
∴前两个数是2,
∵众数2是唯一的,
∴第四个和第五个数不能相同,为5和6,
∴当这5个整数分别是2,2,4,5,6时,和最小,最小是2+2+4+5+6=19,故答案为19.
三.解答题
17.解:当时,这组数据按从小到大顺序排列为x,6,10,12
由题意得
则
当时,这组数据按从小到大顺序排列为6,x,10,12
由题意得
则
当时,这组数据按从小到大顺序排列为6,10,x,12
由题意得
则(舍)
当时,这组数据按从小到大顺序排列为6,10,12,x
由题意得
则
综上所述:或8或16.
18.(1)解:由题意可得:(分)
∴小成同学面试平均成绩为88分;
(2)解:(分)
∴小成同学的最终成绩为分.
19.解:(1)甲的平均成绩(环),
∵乙射击的成绩从小到大从新排列为:3、4、6、7、7、8、8、8、9、10,
∴乙射击成绩的中位数(环),
又∵乙射击的成绩从小到大从新排列为:3、4、6、7、7、8、8、8、9、10,
∴乙射击成绩的众数:c=8(环)
其方差为:
=×(16+9+1+0+3+4+9)
=
=;
(2)从平均成绩看甲、乙二人的成绩相等均为7环,从中位数看甲射中7环以上的次数小于乙,从众数看甲射中7环的次数最多而乙射中8环的次数最多,从方差看甲的成绩比乙的成绩稳定,
综合以上各因素,若选派一名学生参加比赛的话,可选择乙参赛,因为乙获得高分的可能更大.
20.(1)解:根据八年级20名学生成绩,分数段在的有7人,即;
八年级20名学生成绩中,75分的有3人,人数最多,故;
根据八年级分数段可得,中位数在分数段中,将分数段中的分数按照从小到大排列为80,81,82,83,84,85,87,故八年级的中位数是;
故a、b、c的值分别为:7,75,80.5.
(2)解:七、八年级“天宫课堂”竞赛成绩为优秀人数为:人;
故根据抽样调查数据,估计全校七、八年级“天宫课堂”竞赛成绩为优秀(80分及以上)的共有680人.
(3)八年级对“天宫课堂”知识掌握情况更好一些,∵八年级的中位数和众数都高于八年级,且方差小于八年级的方差,说明八年级的成绩更加稳定一些.
21.(1)由题意可得:,
,
由已知可得男生各组人数分别如下:
三组总人数为:,D组:,E组:,
男生成绩按照从低到高排序,排在第和第位的都为,
,
把女生成绩从低到高排序为:,,,,,,,,,,,,,,,,,,,,
根据众数的意义可得,
故答案为:;;;
(2)在本次测试中,男生成绩和女生成绩的平均数相同,女生成绩的中位数与众数都比男生成绩的中位数与众数较高,
此次的体育测试成绩女生更好;
(3)由数据可知:
男生E组数据均为优秀,女生优秀人数为10人,
(人),
该校初2023届参加此次体育测试的学生中成绩为优秀的学生为人.
故答案为:545人.
22.(1)根据数据可知中位数在C组,
由C组数据同学跳绳个数:130,134,135,136,138,140,142,142,143,144,
145,145,147,148,150,152,155,157,158,159.
可得这50名学生1分钟跳绳个数的中位数是137.
故答案为:137.
(2)
答:这50名学生1分钟跳绳个数的平均数为156;
(3)(人)
答:该校八年级学生跳绳成绩优秀的约有368人.
23.(1)解:由条形统计图可得成绩为7环的次数为(次),
故答案为:4;
(2)解:平均数,
众数,
由折线统计图可得剩余两次的成绩和为,
众数为8,
剩余两次的成绩为7和8,
将乙的10次成绩从大到小依次排序为10,9,8,8,8,7,7,6,4,3,
中位数,
故答案为:7,7,7.5;
(3)解:方差,
甲队员的发挥更稳定,理由是方差越小稳定性越好,
故答案为:甲;
(4)解:由题意知,乙队员11次射箭成绩的中位数为,
即乙的11次成绩从大到小依次排序中第6次成绩为8,
,
的最小值为8,
故答案为:8.
.
、
一.选择题(共10小题,满分30分,每小题3分)
1.八(1)班的学生从第一学期到第二学期时,下列有关年龄的统计量不变的是( )
A.平均年龄 B.年龄的方差 C.年龄的众数 D.年龄的中位数
2.小明家至月份的用水量统计如图所示,关于这组数据,下列说法中错误的是( )
A.众数是 吨 B.平均数是 吨 C.中位数是 吨 D.方差是吨
3.某校八年级学生参加每分钟跳绳的测试,并随机抽取部分学生的成绩制成了频数分布直方图(如图),若取每组的组中值作为本小组的均值,则抽取的部分学生每分钟跳绳次数的平均值(结果取整数)为( )
A.87次 B.110次 C.112次 D.120次
4.如图所示的扇形统计图描述了某校学生对课后延时服务的打分情况(满分5分),则所打分数的众数是( )
A.3分 B.3.55分 C.4分 D.
5.八位评委对参加演讲比赛的选手评分,比赛规则规定要去掉一个最高分和一个最低分,然后计算剩下的6个分数的平均分作为选手的比赛得分,规则“去掉一个最高分和一个最低分”一定不会影响这组数据的( )
A.平均数 B.中位数 C.极差 D.众数
6.育新中学八年级六班有53人.一次月考后,数学老师对数学成绩进行了统计.由于有三人因事没有参加本次月考,因此计算其他50人的平均分为90分,方差.后来三进行了补考,数学成绩分别为88分,90分,92分.加入这三人的成绩后,下列说法正确的是( )
A.平均分和方差都改变 B.平均分不变,方差变大
C.平均分不变,方差变小 D.平均分和方差都不变
7.一组数据的方差为,将这组数据中每个数据都除以3,所得新数据的方差是( )
A. B.3 C. D.9
8.(3分)某同学各科成绩如图所示,则其成绩的中位数是( )
A.75分 B.75.5分 C.76分 D.77分
9.第组数据为:,第组数据为:、,其中是正整数.下列结论:
①当时,两组数据的平均数相等;
②当时,第组数据的平均数小于第组数据的平均数;
③当时,第组数据的中位数小于第组数据的中位数;
④当时,第组数据的方差小于第组数据的方差.
其中正确的是( )
A.①② B.②③ C.①③ D.②④
10.某数学兴趣小组对我县祁禄山的红军小道的长度进行次测量,得到个结果,,,…,(单位:).如果用作为这条路线长度的近似值,要使得的值最小,应选取这次测量结果的( )
A.中位数 B.众数 C.平均数 D.最小值
二.填空题(共6小题,满分18分,每小题3分)
11.某学校开展“齐诵满江红,传承报国志”诵读比赛,八年级准备从小乐和小涵两位同学中选拔一位同学参加决赛,如图是小乐和小涵两位同学参加5次选拔赛的测试成绩(满分为100分)折线统计图,若选择一位成绩优异且稳定的同学参赛,推选参加决赛的同学是 (填“小乐”或“小涵”).
12.有一组数据:.将这组数据改变为.设这组数据改变前后的方差分别是,则与的大小关系是 .
13.两组数据:3,a,2b,5与a,6,b的平均数都是6,若将这两组数据合并为一组数据,则这组新数据的众数为 .
14.甲、乙、丙三种糖果的售价分别为每千克6元、每千克7元、每千克8元,若将甲种糖果6千克,乙种糖果10千克,丙种糖果4千克混合在一起,则混合后的糖果的售价应定为每千克 元.
15.若质数a,b满足,则数据a,b,2,3的中位数是 .
16.若五个整数由小到大排列后,中位数为4,唯一的众数为2,则这组数据之和的最小值是 .
三.解答题(共7小题,满分52分)
17.(6分)已知一组数据:x,10,12,6的中位数与平均数相等,求x的值.
18.(6分)校园广播站招聘小记者,对应聘同学分别进行笔试(含阅读能力、思维能力和表达能力三项测试)和面试,应聘者小成同学成绩单位:分如下表:
笔试 面试
成绩 阅读能力 思维能力 表达能力 92
88 90 86
(1)请求出小成同学的笔试平均成绩;
(2)如果笔试平均成绩与面试成绩按的比例确定总成绩,请求出小成同学的总成绩.
19.(8分)甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:
根据以上信息,整理分析数据如下:
平均成绩/环 中位数/环 众数/环 方差
甲
乙
(1)写出表格中的值:
(2)分别运用表中的四个统计量,简要分析这两名队员的射击训练成绩.若选派其中一名参赛,你认为应选哪名队员?
20.(8分)近些年来,我国航天事业飞速发展.今年5月30日,搭载神舟十六号载人飞船的长征二号F遥十六运载火箭,在酒泉卫星发射中心发射升空,神舟十六号航天员乘组由景海鹏、朱杨柱、桂海潮3名航天员组成,发射取得圆满成功.而“天宫课堂”让广大人民尤其是青少年学到了很多科学知识,激发了更多人的航天梦.为普及科学知识,某校开展了“天宫课堂”知识竞赛.为了解七、八年级学生(八年级有600名学生、八年级有800名学生)的竞赛情况,现从两个年级各随机抽取20名学生的成绩(百分制)进行分析.过程如下:
【收集数据】八年级20名学生成绩:62,52,58,67,70,69,75,73,75,75,80,78,77,90,81,84,86,88,94,98;
八年级20名学生成绩在的分数:83,85,87,81,80,84,82;
【整理数据】按照分数段,整理、描述两组样本数据:
年级
八年级 5 a 5 3
八年级 3 6 7 4
【分析数据】两组样本数据的平均数、中位数、众数、方差如表所示:
年级 平均数 中位数 众数 方差
八年级 76.6 76 b 131
八年级 76.6 c 78 124
(1)直接写出a、b、c的值;
(2)根据抽样调查数据,估计全校七、八年级“天宫课堂”竞赛成绩为优秀(80分及以上)的共有多少人?
【得出结论】
(3)通过以上分析,你认为这两个年级中哪个年级对“天宫课堂”知识掌握情况更好一些,并说明推断的合理性(写出一条理由即可).
21.(8分)每年4月中上旬的体育考试,是初三同学们决胜中考的第一关,为了解我校初届学生的体育训练情况,对初届学生进行了一次体育机器模拟测试.测试完成后,在初届的学生中随机抽取了名男生,名女生的本次体育机考的测试成绩,对数据进行整理分析,并给出了下列信息:
①名女生的测试成绩统计如下:,,,,,,,,,,,,,,,,,,,.
②抽取的名男生的测试成绩扇形统计图如图:
③抽取的名男生成绩得分用表示,共分成五组::;:;:;:;:.其中,抽取的名男生的测试成绩中,组的成绩如下:,,,,,.
④抽取男生与女生的学生的测试成绩的平均数、中位数、众数如表所示:
性别 平均数 中位数 众数
女生
男生
(1)根据以上信息可以求出:______,______,______;
(2)结合以上的数据分析,针对本次的体育测试成绩中,你认为此次的体育测试成绩男生与女生谁更好?请说明理由(理由写出一条即可);
(3)若初届学生中男生有人,女生有人,(规定分及以上为优秀)请估计该校初届参加此次体育测试的学生中成绩为优秀的学生人数.
22.(8分)某校为了解八年级800名学生跳绳情况,从八年级学生中随机抽取50名学生进行1分钟跳绳测试,并对测试成绩进行统计,绘制了如下统计表.
组别 1分钟跳绳个数 频数 组内学生平均1分钟跳绳个数
6 80
15 120
20 145
9 180
其中组同学跳绳个数:
130,134,135,136,138,140,142,142,143,144,
145,145,147,148,150,152,155,157,158,159.
根据以上信息,回答下列问题:
(1)这50名学生1分钟跳绳个数的中位数是_______;
(2)求这50名学生1分钟跳绳个数的平均数;
(3)若跳绳个数超过140个为优秀,则该校八年级学生跳绳成绩优秀的约有多少人?
23.(8分)甲、乙两名队员练习射击,每次射击的环数为整数,两人各射击10次,其成绩分别绘制成如图1、图2所示的统计图,两幅图均有部分被污染,两名队员10次的射击成绩整理后,得到的统计表如下表所示.
平均数 中位数 众数 方差
甲 a 7 b 1.8
乙 7 c 8 3
(1)甲队员射中7环的次数为___________;
(2)统计表中___________;___________;___________;
(3)___________队员的发挥更稳定;
(4)乙队员补射1次后,成绩为m环,据统计乙队员这11次射击成绩的中位数比c大0.5,则m的最小值为___________.
答案与试题
选择题
1.B
【分析】根据当数据都加上一个数时的平均数、方差、众数、中位数的变化特征逐项判断即可解答.
【详解】解:由题意知,八年级一班的学生升八年级时,每个同学的年龄都加1,
其中平均年龄加1,众数加1,中位数加1,方差不变,
故A、C、D不符合要求;B符合要求.
故选:B.
2.C
【分析】根据众数、平均数、中位数和方差的定义计算各量,然后对各选项进行判断.
【详解】∵这组数据的6出现了3次,3,4,5各出现了1次,
∴众数为6吨,
∵平均数为吨,方差为吨,中位数是吨,
∴A,B,D选项正确,不符合题意,C选项错误,符合题意,
故选:C
3.C
【分析】根据众数的定义求解即可
【详解】解:∵,
∴由扇形统计图知,得4分的人数占总人数的,人数最多,
所以所打分数的众数为4分,
故选:C.
5.B
【分析】根据平均数、中位数、众数、极差的意义分别判断即可得到答案.
【详解】去掉一个最高分和一个最低分后一定会影响平均分、极差,有可能影响众数,但是这组数据的中间两个数没有变化故一定不会影响中位数,
故选:B.
6.C
【分析】分别求出加入三人成绩后的平均分、方差,然后比较大小即可.
【详解】解:由题意知,加入三人成绩后的平均分为:,
∴平均分不变,
方差为:,
∵,
∴方差变小,
故选:C.
7.C
【分析】本题主要考查的是方差的求法.解答此类问题,通常用x1,x2,…,xn表示出已知数据的平均数与方差,再根据题意用x1,x2,…,xn表示出新数据的平均数与方差,寻找新数据的平均数与原来数据平均数之间的关系.
【详解】设原数据为x1,x2,…,xn,其平均数为,方差为s2.根据题意,得新数据为,,…,,其平均数为.根据方差的定义可知,新数据的方差为.故选C.
【点睛】本题考查平均数与方差,会分别利用方差和平均数的公式去表示方差和平均数是解题的关键.其次根据题意给代数式进行等量变形也非常重要.
8.(3分)(2023春·江西九江·八年级统考期中)某同学各科成绩如图所示,则其成绩的中位数是( )
9.C
【分析】根据平均数的定义,中位数的定义,方差的定义对每一项判断解答即可.
【详解】解:∵第组数据为:,
∴第组数据的平均数为,
∵第组数据为:、,
∴第组数据平均数为,
∵,
∴第组数据平均数,
∴当时,两组数据的平均数相等,
故①正确;
∵当时,,
∴第组数据平均数,
∴第组数据的平均数大于第组数据的平均数,
故②错误;
∵第组数据为:,
∴第组数据的中位数为,
∵第组数据为:、,
∴当时,若为奇数时,第组数据的中位数为;若偶数,第组数据的中位数是为,
∴当时,第组的中位数为,
当时,第组数据的中位数小于第组数据的中位数,
故③正确;
∵第组数据为:,
∴第组数据方差:,
∵第组数据为:、,
∴第组数据的方差为,
∴当时,第组数据的方差等于第组数据的方差,
∴正确的序号为①③,
故选.
10.C
【分析】先设出y=(x﹣x1)2+(x﹣x2)2+(x﹣x3)2+…+(x﹣xn)2,然后进行整理得出y=nx2﹣2(x1+x2+x3+…+xn)x+(x12+x22+x32+…+xn2),再求出二次函数的最小值,再根据x的取值即可得出答案.
【详解】解:设y=(x﹣x1)2+(x﹣x2)2+(x﹣x3)2+…+(x﹣xn)2
y=x2﹣2xx1+x12+x2﹣2xx2+x22+x2﹣2xx3+x32+…+x2﹣2xxn+xn2
y=nx2﹣2(x1+x2+x3+…+xn)x+(x12+x22+x32+…+xn2),
则当x=时,
二次函数y=nx2﹣2(x1+x2+x3+…+xn)x+(x12+x22+x32+…+xn2)最小,
∴x所取平均数时,结果最小,
故选:C.
二.填空题
11.解:根据题意得:
,
,
,
,
,
小涵的成绩优异且稳定,
推选参加决赛的同学是小涵,
故答案为:小涵.
12.
【分析】设数据,,,,的平均数为,根据平均数的定义得出数据,,,,的平均数也为,再利用方差的定义分别求出,,进而比较大小.
【详解】解:设数据,,,,的平均数为,则数据,,,,的平均数也为,
,
,
.
故答案为.
13.8
【分析】根据平均数的意义,求出a、b的值,进而确定两组数据,再合并成一组,找出出现次数最多的数据即可.
【详解】解:由题意得,
,
解得,
这两组数合并成一组新数据为:,
在这组新数据中,出现次数最多的是8,因此众数是8,
故答案为:8.
14.6.9
【分析】先根据甲种糖果6千克,乙种糖果10千克,丙种糖果4千克求出混合后的糖果甲、乙、丙比,再用各自所占比乘各自的售货单价相加即可.
【详解】解:若将甲种糖果6千克,乙种糖果10千克,丙种糖果4千克混合在一起,
则混合后的糖果甲、乙、丙比为,
∴混合后的糖果的售价每千克应定为(元),
故答案为:6.9.
15.4或7
【分析】由题意知,即,且a,b是质数,可得或或或,解方程组可得满足要求的的值,然后根据中位数是第二、三位数的平均数求解即可.
【详解】解:由题意知,即,且a,b是质数,
∴或或或,
解得,,(舍去),(舍去),
当时,2,3,5,7的中位数为;
当时,2,3,11,13的中位数为;
∴数据a,b,2,3的中位数是4或7,
故答案为:4或7.
16.19
【分析】根据“五个整数由小到大排列后,中位数为4,唯一的众数为2”,可知此组数据的第三个数是4,第一个和第二个数是2,据此可知当第四个数是5,第五个数是6时和最小.
【详解】∵中位数为4
∴中间的数为4,
又∵众数是2
∴前两个数是2,
∵众数2是唯一的,
∴第四个和第五个数不能相同,为5和6,
∴当这5个整数分别是2,2,4,5,6时,和最小,最小是2+2+4+5+6=19,故答案为19.
三.解答题
17.解:当时,这组数据按从小到大顺序排列为x,6,10,12
由题意得
则
当时,这组数据按从小到大顺序排列为6,x,10,12
由题意得
则
当时,这组数据按从小到大顺序排列为6,10,x,12
由题意得
则(舍)
当时,这组数据按从小到大顺序排列为6,10,12,x
由题意得
则
综上所述:或8或16.
18.(1)解:由题意可得:(分)
∴小成同学面试平均成绩为88分;
(2)解:(分)
∴小成同学的最终成绩为分.
19.解:(1)甲的平均成绩(环),
∵乙射击的成绩从小到大从新排列为:3、4、6、7、7、8、8、8、9、10,
∴乙射击成绩的中位数(环),
又∵乙射击的成绩从小到大从新排列为:3、4、6、7、7、8、8、8、9、10,
∴乙射击成绩的众数:c=8(环)
其方差为:
=×(16+9+1+0+3+4+9)
=
=;
(2)从平均成绩看甲、乙二人的成绩相等均为7环,从中位数看甲射中7环以上的次数小于乙,从众数看甲射中7环的次数最多而乙射中8环的次数最多,从方差看甲的成绩比乙的成绩稳定,
综合以上各因素,若选派一名学生参加比赛的话,可选择乙参赛,因为乙获得高分的可能更大.
20.(1)解:根据八年级20名学生成绩,分数段在的有7人,即;
八年级20名学生成绩中,75分的有3人,人数最多,故;
根据八年级分数段可得,中位数在分数段中,将分数段中的分数按照从小到大排列为80,81,82,83,84,85,87,故八年级的中位数是;
故a、b、c的值分别为:7,75,80.5.
(2)解:七、八年级“天宫课堂”竞赛成绩为优秀人数为:人;
故根据抽样调查数据,估计全校七、八年级“天宫课堂”竞赛成绩为优秀(80分及以上)的共有680人.
(3)八年级对“天宫课堂”知识掌握情况更好一些,∵八年级的中位数和众数都高于八年级,且方差小于八年级的方差,说明八年级的成绩更加稳定一些.
21.(1)由题意可得:,
,
由已知可得男生各组人数分别如下:
三组总人数为:,D组:,E组:,
男生成绩按照从低到高排序,排在第和第位的都为,
,
把女生成绩从低到高排序为:,,,,,,,,,,,,,,,,,,,,
根据众数的意义可得,
故答案为:;;;
(2)在本次测试中,男生成绩和女生成绩的平均数相同,女生成绩的中位数与众数都比男生成绩的中位数与众数较高,
此次的体育测试成绩女生更好;
(3)由数据可知:
男生E组数据均为优秀,女生优秀人数为10人,
(人),
该校初2023届参加此次体育测试的学生中成绩为优秀的学生为人.
故答案为:545人.
22.(1)根据数据可知中位数在C组,
由C组数据同学跳绳个数:130,134,135,136,138,140,142,142,143,144,
145,145,147,148,150,152,155,157,158,159.
可得这50名学生1分钟跳绳个数的中位数是137.
故答案为:137.
(2)
答:这50名学生1分钟跳绳个数的平均数为156;
(3)(人)
答:该校八年级学生跳绳成绩优秀的约有368人.
23.(1)解:由条形统计图可得成绩为7环的次数为(次),
故答案为:4;
(2)解:平均数,
众数,
由折线统计图可得剩余两次的成绩和为,
众数为8,
剩余两次的成绩为7和8,
将乙的10次成绩从大到小依次排序为10,9,8,8,8,7,7,6,4,3,
中位数,
故答案为:7,7,7.5;
(3)解:方差,
甲队员的发挥更稳定,理由是方差越小稳定性越好,
故答案为:甲;
(4)解:由题意知,乙队员11次射箭成绩的中位数为,
即乙的11次成绩从大到小依次排序中第6次成绩为8,
,
的最小值为8,
故答案为:8.
.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
