9.2.4 总体离散程度的估计 课件(共39张PPT)高一下学期数学人教A版(2019)必修二
文档属性
| 名称 | 9.2.4 总体离散程度的估计 课件(共39张PPT)高一下学期数学人教A版(2019)必修二 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-14 00:00:00 | ||
图片预览











文档简介
(共39张PPT)
第九章 >》
统计
9.2 用样本估计总体
9.2.4 总体离散程度的估计
学习目标
活动方案 检测反馈
学习目标
1.结合实例,能用样本估计总体的离散程度参数(标准差、方 差、极差).
2.理解离散程度参数的统计含义.
活动方案
活 动 一 极差、方差、标准差的概念
— 《 背景引入 》—
有两位射击运动员在一次射击测试中各射靶10次,每次命中的环数 如下:
甲 7 8 7 9 5 4 9 10 7 4
乙 9 5 7 8 7 6 8 6 7 7
如果你是教练,你如何对两位运动员的射击情况作出评价 如果这 是一次选拔性考核,你应当如何作出选择
内容索引
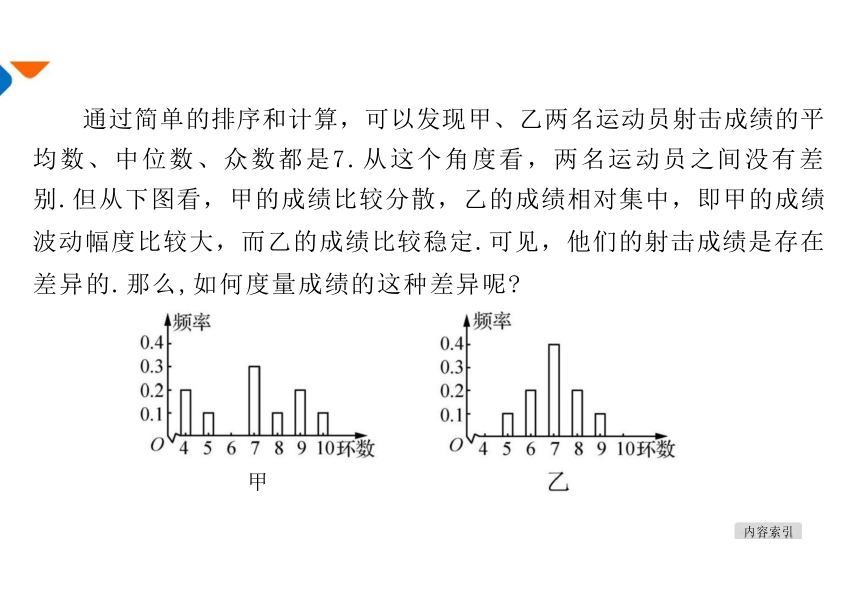
均数、中位数、众数都是7.从这个角度看,两名运动员之间没有差
别.但从下图看,甲的成绩比较分散,乙的成绩相对集中,即甲的成绩 波动幅度比较大,而乙的成绩比较稳定.可见,他们的射击成绩是存在 差异的.那么,如何度量成绩的这种差异呢
通过简单的排序和计算,可以发现甲、乙两名运动员射击成绩的平
内容索引
甲
【解析】如果射击的成绩很稳定,那么大多数的射击成绩离平均成 绩不会太远;相反,如果射击的成绩波动幅度很大,那么大多数的射击 成绩离平均成绩会比较远.因此,我们可以通过这两组射击成绩与它们 的平均成绩的“平均距离”来度量成绩的波动幅度.
思考
极差在一定程度上刻画了数据的离散程度,但只用了数据最大、最 小两个值,如要考虑两个运动员的成绩的稳定性,应该用什么去衡量
内容索引
方差与标准差的定义及公式:
在一组数据x ,x ,…,xn 中,各数据与它们的平均数x 的差的平方
的平均数,叫作这组数据的方差,常用s 表示,即 方差
的算术平方根叫作这组数据的标准差,用s 表示,即
内 容 索 引
s=√s =√ 10.5≈3.24.
练习 求52,49,48,55,47,48,56,53的方差及标准差.
内容索引
体均值类似,总体方差也可以写成加权的形式.如果总体的 N 个变量值
中,不同的值共有k(k≤N)个,不妨记为Y,Y ,…,Yk, 其 中Yi出现的
频数为f(i=1,2, … ,k), 则总体方差为
内 容 索 引
小 结
总体方差、总体标准差与样本方差、样本标准差的区别与联系:
(1)如果总体中所有个体的变量值分别为Y,Y , …,YN, 总体平均
为总体方差,S=S 为总体标准差.与总
数为Y, 则 称
(2)如果一个样本中个体的变量值分别为y ,y , …,yn, 样本平均
数为y, 则称 为样本方差,s=√s 为样本标准差.
内 容 索 引
活 动二掌握极差、方差、标准差的应用
例1 在对树人中学高一年级学生身高的调查中,采用样本量比例分 配的分层随机抽样,如果不知道样本数据,只知道抽取了男生23人,其 平均数和方差分别为170.6和12.59,抽取了女生27人,其平均数和方差分 别为160.6和38.62.你能由这些数据计算出总样本的方差,并对高一年级 全体学生的身高方差作出估计吗
内容索引
记为s ; 把女生样本记为y ,y , … ,y 7, 其平均数记为y, 方差记为
把总样本数据的平均数记为2,方差记为s .
根据方差的定义,总样本方差为
【解析】把男生样本记为 x ,x ,…,x 3, 其平均数记为x, 方差
内容索引
心
●
同理可
内容索引
所以
由x=170.6,y=160.6, 根据按比例分配分层随机抽样总样本平均数 与各层样本平均数的关系,可得总样本平均数为
内容索引
把已知的男生、女生样本平均数和方差的取值代入①,可得 {23×[12.59+(170.6—165.2) ]+27×[38.62+(160.6—165.2) ]}=51.4862.
我们可以计算出总样本的方差为51.4862,并据此估计高一年级学生 身高的总体方差为51.4862.
内容索引
1.标准差代表数据的离散程度,考虑数据范围时需要加减标准差.
2.计算样本平均数、样本方差直接利用公式,注意公式的变形和整 体代换.
内容索引
【解析】把专业人士打分样本记为x ,x , …,xg, 其平均数记为x,
方差记为s ; 把观众代表打分样本记为y ,y , … ,y , 其平均数为y,
方差记为s ; 把总体数据的平均数记为2,方差记为s ,
在一个文艺比赛中,8名专业人士和12名观众代表各组成一个评判小
组,给参赛选手打分.在给某选手的打分中,专业人士打分的平均数和 标准差分别为47.4和3.7,观众代表打分的平均数和标准差分别为56.2和 11.8,试根据这些数据计算这名选手得分的平均数和方差.
跟踪训练
内容索引
所以这名选手得分的平均数为52.68分,方差为107.6.
则总样本平均数为
总样本方差为
内容索引
≈10
使用 天数 151~ 180 181 210 211 240 241 270 271 300 301 330 331 360
361
390
日光 灯数 1 11 18 20 25 16 7
2
例2 为了保护学生的视力,教室内的日光灯在使用一段时间后必须
更换.已知某校使用的100只日光灯在必须换掉前的使用天数如下:
试估计这种日光灯使用寿命的平均数和标准差.
内容索引
255.5,285.5,315.5,345.5,375.5,
由此算得平均数约为165.5×1%+195.5×11%+225.5×18%十 255.5×20%+285.5×25%+315.5×16%+345.5×7%+375.5×2%=
268.4~268.
这些组中值的方差 +18×(225.5—268.4) +20×(255.5—268.4) +25×(285.5—268.4) +
16×(315.5—268.4) +7×(345.5—268.4) +2×(375.5—268.4) ]=
2128.59,
【解析】 各区间的组中值分别为165.5,195.5,225.5,
内容索引
故所求的标准差约为 √2128.59≈46,
故估计这种日光灯使用寿命的平均数为268天,标准差约为46天.
内容索引
对一组数据的评价,有多个角度,平均数、标准差等数值都是反映
这组数据的客观情况,根据实际需要确定求哪些数值.
内容索引
有一种鱼的身体吸收汞,身体中汞的含量超过其体重的1.00 ppm (即
百万分之一)的鱼被人食用后,就会对人体产生危害.在30条鱼的样本中 发现的汞含量(单位:ppm) 如下:
0.07 0.24 0.95 0.98 1.02 0.98 1.37 1.40 0.39
1.02
1.44 1.58 0.54 1.08 0.61 0.72 1.20 1.14 1.62
1.68
1.85 1.20 0.81 0.82 0.84 1.29 1.26 2.10 0.91
1.31
内 容 索 引
(1)请用合适的统计图描述上述数据,并分析这30条鱼的汞含量的分 布特点;
(2)求出上述样本数据的平均数和标准差;
(3)从实际情况看,许多鱼的汞含量超标的原因是这些鱼在出售之前 没有被检测过,你认为每批这种鱼的平均汞含量都比1.00 ppm 大吗
(4)在上述样本中,有多少条鱼的汞含量在以平均数为中心、距离平 均数为2倍标准差的范围内
内容索引
分组 频数
频率
[0.00,0.50] 3
0.10
[0.50,1.00] 10
0.33
(1.00,1.50) 12
0.40
[1.50,2.00] 4
0.13
[2.00,2.50] 1
0.03
合计 30
1.00
【解析】(1)频率分布表如下:
内容索引
作出如图所示的统计图如图:
A频率/组距
0.8
0.6
0.4
0.2
0 0.51.01.52.02.5汞含量/ppm
汞含量的分布偏向于1.00 ppm 的方向,即多数鱼的汞含量分布在大
于1.00 ppm 的区域.
内容索引
2.25×0.03≈1.07(ppm),
样本方差s ≈(0.25—1.07) ×0.1+(0.75—1.07) ×0.33+(1.25— 1.07) ×0.4+(1.75—1.07) ×0.13+(2.25—1.07) ×0.03≈0.22,
标准差s=√0.22≈0.47.
(3)不一定,因为我们不知道其他各批鱼的汞含量分布是否都和这 批鱼相同,即使其他各批鱼的汞含量分布与这批鱼相同,上面的数据也
只能为这个分布作出估计,不能保证每批鱼的平均汞含量都大于1.00
ppm.
(4)由题意得,该范围为(0.13,2.01),所以有28条鱼的汞含量在以平 均数为中心、距离平均数为2倍标准差的范围内.
内容索引
(2)样本平均数x≈0.25×0.1+0.75×0.33+1.25×0.4+1.75×0.13+
1. (2022葫芦岛一模)有一组样本数据x ,X , …,xn, 由这组数据得
到新样本数据y ,y ,…,yn, 其中y;=x;+c(i=1,2,…,n),c 为非零实 数,则下列关于这两组样本数据的结论中正确的是( )
A.平均数相同 B.众数相同
C.中位数相同 D.极差相同
【解析】设样本数据x ,x ,…,xn 的平均数为x, 众数为m, 中位 数为a, 极差为b=xmax一Xmin,则新样本数据y ,y ,…,yn 的平均数为x 十c, 众数为m+c, 中位数为a+c, 极差为ymax一Ymin=(xmax+c)一(xmin十 c)=b, 所以两组样本数据的极差相等.
【答案】D
内容索引
1
4 5
2
3
第一组 第二组 第三组 第四组
A. 第一组 B. 第二组
C. 第三组 D. 第四组
2 . 样 本 量 为 9 的 四 组 数 据 , 它 们 的 平 均 数 都 是 5 , 条 形 图 如 图 所 示 ,
则标准差最大的一组是( )
频率
1.0
0.4
0.3
0
45 6 数据
频率
1.0
0
5
内容索引
数据
2 3
4
5
1
【解析】第一组中,样本数据都为5,数据没有波动幅度,标准差
为0;第二组中,样本数据为4,4,4,5,5,5,6,6,6,标准差 第三组中,
第四组中,样本数据为
2,2,2,2,5,8,8,8,8,标准差为2 √2,故标准差最大的一组是第四组.
样本数据为3,3,4,4,5,6,6,7,7,标准差为
【答案】D
内容索引
2 3
4
5
1
则下列说法中正确的是( )
A.甲运动员得分的极差小于乙运动员得分的极差
B. 甲运动员得分的中位数小于乙运动员得分的中位数 C. 甲运动员得分的平均值大于乙运动员得分的平均值 D. 甲运动员的成绩比乙运动员的成绩稳定
场次 1 2 3 4 5
6
甲得分 31 16 24 34 18
9
乙得分 23 21 32 11 35
10
3. (多选)某赛季甲、乙两名篮球运动员各6场比赛得分情况如下表:
内容索引
4
2
5
1
【解析】由题意,得甲的极差为34—9=25,中位数是21,均值为 22,方差为s通=75,同样乙的极差为35—10=25,中位数是22,均值为 22,方差为s ≈89.3. 故选BD.
【答案】BD
内容索引
4
2
5
1
4.若给定一组数据x ,X , …,xn, 方差为s .
(1)ax ,ax ,…,axn 的方差是 a s ;
(2)ax +b,ax +b,…,axn+b 的方差是 a s
内 容 索 引
1 2
4 5
3
5.一个小商店从一家有限公司购进21袋白糖,每袋白糖的标准质量
是500 g, 为了了解这些白糖的质量情况,称出各袋白糖的质量(单位: g) 如下:486,495,496,498,499,493,493,498,484,497,504,489,495,503,499,503, 509,498,487,500,508.
(1)21袋白糖的平均质量是多少 标准差s是多少
(2)质量位于x-s 与x+s 之间有多少袋白糖 所占的百分比是多 少
内 容 索 引
2 3
4
1
【解析】(1)平均质量 486+495+296+…+508≈496.9,
×[(486-496.9) +(495-496.9) +…+(508-496.9) ]≈42.89, 所以s= √42.89≈6.55.
(2)质量位于x—s 与x+s 之间等于在区间(490.35,503.45)上的白糖的 袋数,共有14袋,
所占的百分比
内容索引
4
2
3
1
谢谢观看
Thankyou for watching
第九章 >》
统计
9.2 用样本估计总体
9.2.4 总体离散程度的估计
学习目标
活动方案 检测反馈
学习目标
1.结合实例,能用样本估计总体的离散程度参数(标准差、方 差、极差).
2.理解离散程度参数的统计含义.
活动方案
活 动 一 极差、方差、标准差的概念
— 《 背景引入 》—
有两位射击运动员在一次射击测试中各射靶10次,每次命中的环数 如下:
甲 7 8 7 9 5 4 9 10 7 4
乙 9 5 7 8 7 6 8 6 7 7
如果你是教练,你如何对两位运动员的射击情况作出评价 如果这 是一次选拔性考核,你应当如何作出选择
内容索引
均数、中位数、众数都是7.从这个角度看,两名运动员之间没有差
别.但从下图看,甲的成绩比较分散,乙的成绩相对集中,即甲的成绩 波动幅度比较大,而乙的成绩比较稳定.可见,他们的射击成绩是存在 差异的.那么,如何度量成绩的这种差异呢
通过简单的排序和计算,可以发现甲、乙两名运动员射击成绩的平
内容索引
甲
【解析】如果射击的成绩很稳定,那么大多数的射击成绩离平均成 绩不会太远;相反,如果射击的成绩波动幅度很大,那么大多数的射击 成绩离平均成绩会比较远.因此,我们可以通过这两组射击成绩与它们 的平均成绩的“平均距离”来度量成绩的波动幅度.
思考
极差在一定程度上刻画了数据的离散程度,但只用了数据最大、最 小两个值,如要考虑两个运动员的成绩的稳定性,应该用什么去衡量
内容索引
方差与标准差的定义及公式:
在一组数据x ,x ,…,xn 中,各数据与它们的平均数x 的差的平方
的平均数,叫作这组数据的方差,常用s 表示,即 方差
的算术平方根叫作这组数据的标准差,用s 表示,即
内 容 索 引
s=√s =√ 10.5≈3.24.
练习 求52,49,48,55,47,48,56,53的方差及标准差.
内容索引
体均值类似,总体方差也可以写成加权的形式.如果总体的 N 个变量值
中,不同的值共有k(k≤N)个,不妨记为Y,Y ,…,Yk, 其 中Yi出现的
频数为f(i=1,2, … ,k), 则总体方差为
内 容 索 引
小 结
总体方差、总体标准差与样本方差、样本标准差的区别与联系:
(1)如果总体中所有个体的变量值分别为Y,Y , …,YN, 总体平均
为总体方差,S=S 为总体标准差.与总
数为Y, 则 称
(2)如果一个样本中个体的变量值分别为y ,y , …,yn, 样本平均
数为y, 则称 为样本方差,s=√s 为样本标准差.
内 容 索 引
活 动二掌握极差、方差、标准差的应用
例1 在对树人中学高一年级学生身高的调查中,采用样本量比例分 配的分层随机抽样,如果不知道样本数据,只知道抽取了男生23人,其 平均数和方差分别为170.6和12.59,抽取了女生27人,其平均数和方差分 别为160.6和38.62.你能由这些数据计算出总样本的方差,并对高一年级 全体学生的身高方差作出估计吗
内容索引
记为s ; 把女生样本记为y ,y , … ,y 7, 其平均数记为y, 方差记为
把总样本数据的平均数记为2,方差记为s .
根据方差的定义,总样本方差为
【解析】把男生样本记为 x ,x ,…,x 3, 其平均数记为x, 方差
内容索引
心
●
同理可
内容索引
所以
由x=170.6,y=160.6, 根据按比例分配分层随机抽样总样本平均数 与各层样本平均数的关系,可得总样本平均数为
内容索引
把已知的男生、女生样本平均数和方差的取值代入①,可得 {23×[12.59+(170.6—165.2) ]+27×[38.62+(160.6—165.2) ]}=51.4862.
我们可以计算出总样本的方差为51.4862,并据此估计高一年级学生 身高的总体方差为51.4862.
内容索引
1.标准差代表数据的离散程度,考虑数据范围时需要加减标准差.
2.计算样本平均数、样本方差直接利用公式,注意公式的变形和整 体代换.
内容索引
【解析】把专业人士打分样本记为x ,x , …,xg, 其平均数记为x,
方差记为s ; 把观众代表打分样本记为y ,y , … ,y , 其平均数为y,
方差记为s ; 把总体数据的平均数记为2,方差记为s ,
在一个文艺比赛中,8名专业人士和12名观众代表各组成一个评判小
组,给参赛选手打分.在给某选手的打分中,专业人士打分的平均数和 标准差分别为47.4和3.7,观众代表打分的平均数和标准差分别为56.2和 11.8,试根据这些数据计算这名选手得分的平均数和方差.
跟踪训练
内容索引
所以这名选手得分的平均数为52.68分,方差为107.6.
则总样本平均数为
总样本方差为
内容索引
≈10
使用 天数 151~ 180 181 210 211 240 241 270 271 300 301 330 331 360
361
390
日光 灯数 1 11 18 20 25 16 7
2
例2 为了保护学生的视力,教室内的日光灯在使用一段时间后必须
更换.已知某校使用的100只日光灯在必须换掉前的使用天数如下:
试估计这种日光灯使用寿命的平均数和标准差.
内容索引
255.5,285.5,315.5,345.5,375.5,
由此算得平均数约为165.5×1%+195.5×11%+225.5×18%十 255.5×20%+285.5×25%+315.5×16%+345.5×7%+375.5×2%=
268.4~268.
这些组中值的方差 +18×(225.5—268.4) +20×(255.5—268.4) +25×(285.5—268.4) +
16×(315.5—268.4) +7×(345.5—268.4) +2×(375.5—268.4) ]=
2128.59,
【解析】 各区间的组中值分别为165.5,195.5,225.5,
内容索引
故所求的标准差约为 √2128.59≈46,
故估计这种日光灯使用寿命的平均数为268天,标准差约为46天.
内容索引
对一组数据的评价,有多个角度,平均数、标准差等数值都是反映
这组数据的客观情况,根据实际需要确定求哪些数值.
内容索引
有一种鱼的身体吸收汞,身体中汞的含量超过其体重的1.00 ppm (即
百万分之一)的鱼被人食用后,就会对人体产生危害.在30条鱼的样本中 发现的汞含量(单位:ppm) 如下:
0.07 0.24 0.95 0.98 1.02 0.98 1.37 1.40 0.39
1.02
1.44 1.58 0.54 1.08 0.61 0.72 1.20 1.14 1.62
1.68
1.85 1.20 0.81 0.82 0.84 1.29 1.26 2.10 0.91
1.31
内 容 索 引
(1)请用合适的统计图描述上述数据,并分析这30条鱼的汞含量的分 布特点;
(2)求出上述样本数据的平均数和标准差;
(3)从实际情况看,许多鱼的汞含量超标的原因是这些鱼在出售之前 没有被检测过,你认为每批这种鱼的平均汞含量都比1.00 ppm 大吗
(4)在上述样本中,有多少条鱼的汞含量在以平均数为中心、距离平 均数为2倍标准差的范围内
内容索引
分组 频数
频率
[0.00,0.50] 3
0.10
[0.50,1.00] 10
0.33
(1.00,1.50) 12
0.40
[1.50,2.00] 4
0.13
[2.00,2.50] 1
0.03
合计 30
1.00
【解析】(1)频率分布表如下:
内容索引
作出如图所示的统计图如图:
A频率/组距
0.8
0.6
0.4
0.2
0 0.51.01.52.02.5汞含量/ppm
汞含量的分布偏向于1.00 ppm 的方向,即多数鱼的汞含量分布在大
于1.00 ppm 的区域.
内容索引
2.25×0.03≈1.07(ppm),
样本方差s ≈(0.25—1.07) ×0.1+(0.75—1.07) ×0.33+(1.25— 1.07) ×0.4+(1.75—1.07) ×0.13+(2.25—1.07) ×0.03≈0.22,
标准差s=√0.22≈0.47.
(3)不一定,因为我们不知道其他各批鱼的汞含量分布是否都和这 批鱼相同,即使其他各批鱼的汞含量分布与这批鱼相同,上面的数据也
只能为这个分布作出估计,不能保证每批鱼的平均汞含量都大于1.00
ppm.
(4)由题意得,该范围为(0.13,2.01),所以有28条鱼的汞含量在以平 均数为中心、距离平均数为2倍标准差的范围内.
内容索引
(2)样本平均数x≈0.25×0.1+0.75×0.33+1.25×0.4+1.75×0.13+
1. (2022葫芦岛一模)有一组样本数据x ,X , …,xn, 由这组数据得
到新样本数据y ,y ,…,yn, 其中y;=x;+c(i=1,2,…,n),c 为非零实 数,则下列关于这两组样本数据的结论中正确的是( )
A.平均数相同 B.众数相同
C.中位数相同 D.极差相同
【解析】设样本数据x ,x ,…,xn 的平均数为x, 众数为m, 中位 数为a, 极差为b=xmax一Xmin,则新样本数据y ,y ,…,yn 的平均数为x 十c, 众数为m+c, 中位数为a+c, 极差为ymax一Ymin=(xmax+c)一(xmin十 c)=b, 所以两组样本数据的极差相等.
【答案】D
内容索引
1
4 5
2
3
第一组 第二组 第三组 第四组
A. 第一组 B. 第二组
C. 第三组 D. 第四组
2 . 样 本 量 为 9 的 四 组 数 据 , 它 们 的 平 均 数 都 是 5 , 条 形 图 如 图 所 示 ,
则标准差最大的一组是( )
频率
1.0
0.4
0.3
0
45 6 数据
频率
1.0
0
5
内容索引
数据
2 3
4
5
1
【解析】第一组中,样本数据都为5,数据没有波动幅度,标准差
为0;第二组中,样本数据为4,4,4,5,5,5,6,6,6,标准差 第三组中,
第四组中,样本数据为
2,2,2,2,5,8,8,8,8,标准差为2 √2,故标准差最大的一组是第四组.
样本数据为3,3,4,4,5,6,6,7,7,标准差为
【答案】D
内容索引
2 3
4
5
1
则下列说法中正确的是( )
A.甲运动员得分的极差小于乙运动员得分的极差
B. 甲运动员得分的中位数小于乙运动员得分的中位数 C. 甲运动员得分的平均值大于乙运动员得分的平均值 D. 甲运动员的成绩比乙运动员的成绩稳定
场次 1 2 3 4 5
6
甲得分 31 16 24 34 18
9
乙得分 23 21 32 11 35
10
3. (多选)某赛季甲、乙两名篮球运动员各6场比赛得分情况如下表:
内容索引
4
2
5
1
【解析】由题意,得甲的极差为34—9=25,中位数是21,均值为 22,方差为s通=75,同样乙的极差为35—10=25,中位数是22,均值为 22,方差为s ≈89.3. 故选BD.
【答案】BD
内容索引
4
2
5
1
4.若给定一组数据x ,X , …,xn, 方差为s .
(1)ax ,ax ,…,axn 的方差是 a s ;
(2)ax +b,ax +b,…,axn+b 的方差是 a s
内 容 索 引
1 2
4 5
3
5.一个小商店从一家有限公司购进21袋白糖,每袋白糖的标准质量
是500 g, 为了了解这些白糖的质量情况,称出各袋白糖的质量(单位: g) 如下:486,495,496,498,499,493,493,498,484,497,504,489,495,503,499,503, 509,498,487,500,508.
(1)21袋白糖的平均质量是多少 标准差s是多少
(2)质量位于x-s 与x+s 之间有多少袋白糖 所占的百分比是多 少
内 容 索 引
2 3
4
1
【解析】(1)平均质量 486+495+296+…+508≈496.9,
×[(486-496.9) +(495-496.9) +…+(508-496.9) ]≈42.89, 所以s= √42.89≈6.55.
(2)质量位于x—s 与x+s 之间等于在区间(490.35,503.45)上的白糖的 袋数,共有14袋,
所占的百分比
内容索引
4
2
3
1
谢谢观看
Thankyou for watching
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
