吉林省吉林市2023-2024学年高一下学期期末考试数学试题(含答案)
文档属性
| 名称 | 吉林省吉林市2023-2024学年高一下学期期末考试数学试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-13 15:19:28 | ||
图片预览




文档简介
吉林市普通高中2023-2024学年度高一年级下学期期末调研测试
数 学 试 题
说明:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上,贴好条形码。
2.答选择题时,选出每小题答案后,用2b铅笔把答题卡对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。答非选择题时,用0.5毫米的黑色签字笔将答案写在答题卡上。字体工整,笔迹清楚。
3.请按题号顺序在答题卡相应区域作答,超出区域所写答案无效;在试卷上、草纸上答题无效。
4.考试结束后,将本试卷和答题卡一并交回。
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个是符合题目要求.
1.已知样本数据:,,,,,,则这组样本数据的中位数为
A. B. C. D.
2.已知复数,则的模为
A. B. C. D.
3.若,是两条直线,是一个平面,则下列命题中正确的是
A.若,,则 B.若,,则
C.若,,则 D.若,,则
4.已知的内角,,的对边分别为,,,若,,,则
A. B. C. D.
5.已知圆锥的侧面展开图是半径为,圆心角为的扇形,则该圆锥的表面积为
A. B. C. D.
6.在中,,则
A. B.
C. D.
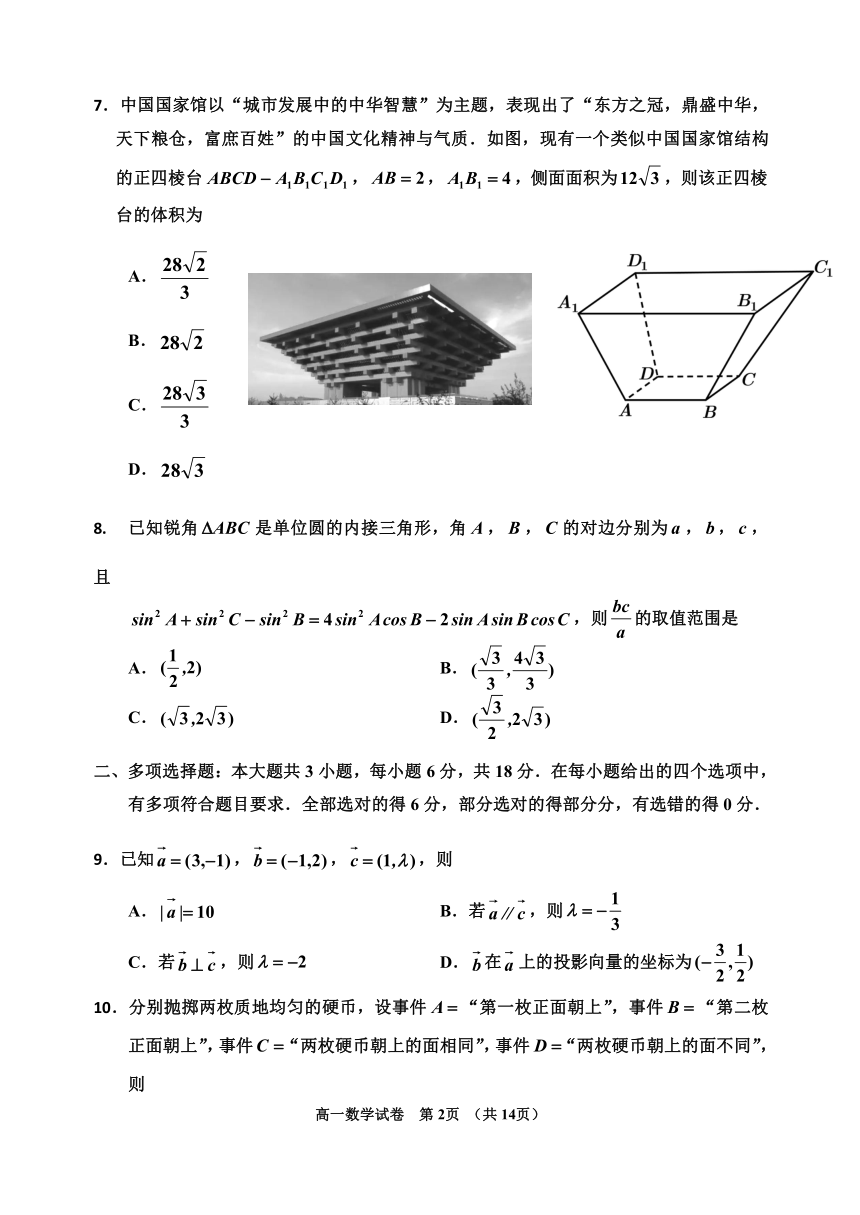
7.中国国家馆以“城市发展中的中华智慧”为主题,表现出了“东方之冠,鼎盛中华,天下粮仓,富庶百姓”的中国文化精神与气质.如图,现有一个类似中国国家馆结构的正四棱台,,,侧面面积为,则该正四棱台的体积为
A.
B.
C.
D.
已知锐角是单位圆的内接三角形,角,,的对边分别为,,,且
,则的取值范围是
A. B.
C. D.
二、多项选择题:本大题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.已知,,,则
A. B.若,则
C.若,则 D.在上的投影向量的坐标为
10.分别抛掷两枚质地均匀的硬币,设事件“第一枚正面朝上”,事件“第二枚正面朝上”,事件“两枚硬币朝上的面相同”,事件“两枚硬币朝上的面不同”,则
A. B.与互斥
C.与互为对立 D.与相互独立
11.如图,在棱长为的正方体中,,分别是棱,的中点,则
A.三棱锥的外接球的表面积为
B.三棱锥的外接球的体积为
C.点到平面的距离为
D.已知点是底面(不含边界)内一动点,
且平面,则线段的长度的取值范围是
三、填空题:本大题共3小题,每小题5分,共15分.其中第14题的第一个空填对得2分, 第二个空填对得3分.
12.已知是关于的方程的一个根,则实数 .
13.在中,,,为中点,则 .
14.我国古代数学家祖暅于世纪末提出了下面的体积计算原理:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面面积总相等,那么这两个几何体的体积相等.在正四棱柱中,,是上一点,于点,设,,则点绕旋转一周所得的圆的面积为 (用表示);将空间四边形绕旋转一周所得几何体的体积为 .
四、解答题:本大题共5小题,共77分.解答应写出文字说明,证明过程或演算步骤.
15.(本小题满分13分)
某高校强基计划考试分“笔试”和“面试”两部分,每部分考试成绩记“合格”或“不合格”.两部分考试成绩均“合格”者则考试“通过”,并给予录取.现甲、乙两人都参加此高校的强基计划考试,甲、乙在笔试中成绩“合格”的概率分别为,,在面试中成绩“合格”的概率分别为,,且每人在笔试和面试成绩是否“合格”是相互独立的.
(Ⅰ)甲、乙两人谁被录取的可能性大,并说明理由;
(Ⅱ)求甲、乙两人中至少有一人被录取的概率.
16.(本小题满分15分)
如图,测量河对岸的塔高时,可以选取与塔底在同一水平面内的两个测量基点与.现测得,,,并在点处测得塔顶的仰角.
(Ⅰ)求与两点间的距离;
(Ⅱ)求塔高.
17.(本小题满分15分)
随着全民健身意识增强,马拉松运动逐渐成为深受群众喜爱的体育健身项目之一.吉林市自年以来,现已成功举办五届马拉松比赛,“吉马”也因此成为了东北地区乃至全国颇具影响力的品牌赛事.年“吉马”被中国田径协会评为“城市形象媒体传播赛事典型案例”.时隔一年,吉林市委、市政府再次启动这一国际化赛事,将挑战自我、超越极限、坚韧不拔、永不放弃的马拉松精神与我市激流勇进的城市精神相结合,并将其发扬光大.为此,某校举办了“吉马”知识竞赛,从所有竞赛成绩中抽取一个容量为的样本,并按竞赛成绩(单位:分)分成六组:,,,,,,得到如下图所示的频率分布直方图.
(Ⅰ)求频率分布直方图中的值,并求样本中竞赛成绩的第百分位数;
(Ⅱ)现从样本中竞赛成绩在内用比例分配的分层随机抽样的方法抽取人,再从这人中抽取人座谈,求至少有一人竞赛成绩在内的概率;
(Ⅲ)已知样本中竞赛成绩在内的平均数,方差,样本中竞赛成绩在内的平均数,方差,并据此估计所有答卷中竞赛成绩在内的总体方差.
参考公式:总体分为层,通过分层随机抽样,各层抽取的样本量、样本平均数和样本方差分别为:;.记总的样本平均数为,样本方差为,.
18.(本小题满分17分)
如图,在四棱锥中,,,,且是的中点.
(Ⅰ)求证:平面;
(Ⅱ)若平面平面,且,.
(i)求证:平面;
(ii)求直线与平面所成的角的正弦值.
19.(本小题满分17分)
法国伟大的军事家、政治家拿破仑一生钟爱数学,他发现并证明了著名的拿破仑定理 :“以任意的三角形的三条边为边向外构造三个等边三角形,则这三个等边三角形的中心恰
为另一个等边三角形的顶点”.如图,的内角,,的对边分别为,,,,以,,为边向外作三个等边三角形,其中心分别为,,.
(Ⅰ)求角;
(Ⅱ)若,且的周长为,求;
(Ⅲ)若的面积为,求的角平分线的取值范围.
★ 保密·启用前 ★
高一数学试卷 第1页 (共6页)
数 学 试 题
说明:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上,贴好条形码。
2.答选择题时,选出每小题答案后,用2b铅笔把答题卡对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。答非选择题时,用0.5毫米的黑色签字笔将答案写在答题卡上。字体工整,笔迹清楚。
3.请按题号顺序在答题卡相应区域作答,超出区域所写答案无效;在试卷上、草纸上答题无效。
4.考试结束后,将本试卷和答题卡一并交回。
一、单项选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个是符合题目要求.
1.已知样本数据:,,,,,,则这组样本数据的中位数为
A. B. C. D.
2.已知复数,则的模为
A. B. C. D.
3.若,是两条直线,是一个平面,则下列命题中正确的是
A.若,,则 B.若,,则
C.若,,则 D.若,,则
4.已知的内角,,的对边分别为,,,若,,,则
A. B. C. D.
5.已知圆锥的侧面展开图是半径为,圆心角为的扇形,则该圆锥的表面积为
A. B. C. D.
6.在中,,则
A. B.
C. D.
7.中国国家馆以“城市发展中的中华智慧”为主题,表现出了“东方之冠,鼎盛中华,天下粮仓,富庶百姓”的中国文化精神与气质.如图,现有一个类似中国国家馆结构的正四棱台,,,侧面面积为,则该正四棱台的体积为
A.
B.
C.
D.
已知锐角是单位圆的内接三角形,角,,的对边分别为,,,且
,则的取值范围是
A. B.
C. D.
二、多项选择题:本大题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.已知,,,则
A. B.若,则
C.若,则 D.在上的投影向量的坐标为
10.分别抛掷两枚质地均匀的硬币,设事件“第一枚正面朝上”,事件“第二枚正面朝上”,事件“两枚硬币朝上的面相同”,事件“两枚硬币朝上的面不同”,则
A. B.与互斥
C.与互为对立 D.与相互独立
11.如图,在棱长为的正方体中,,分别是棱,的中点,则
A.三棱锥的外接球的表面积为
B.三棱锥的外接球的体积为
C.点到平面的距离为
D.已知点是底面(不含边界)内一动点,
且平面,则线段的长度的取值范围是
三、填空题:本大题共3小题,每小题5分,共15分.其中第14题的第一个空填对得2分, 第二个空填对得3分.
12.已知是关于的方程的一个根,则实数 .
13.在中,,,为中点,则 .
14.我国古代数学家祖暅于世纪末提出了下面的体积计算原理:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截得的两个截面面积总相等,那么这两个几何体的体积相等.在正四棱柱中,,是上一点,于点,设,,则点绕旋转一周所得的圆的面积为 (用表示);将空间四边形绕旋转一周所得几何体的体积为 .
四、解答题:本大题共5小题,共77分.解答应写出文字说明,证明过程或演算步骤.
15.(本小题满分13分)
某高校强基计划考试分“笔试”和“面试”两部分,每部分考试成绩记“合格”或“不合格”.两部分考试成绩均“合格”者则考试“通过”,并给予录取.现甲、乙两人都参加此高校的强基计划考试,甲、乙在笔试中成绩“合格”的概率分别为,,在面试中成绩“合格”的概率分别为,,且每人在笔试和面试成绩是否“合格”是相互独立的.
(Ⅰ)甲、乙两人谁被录取的可能性大,并说明理由;
(Ⅱ)求甲、乙两人中至少有一人被录取的概率.
16.(本小题满分15分)
如图,测量河对岸的塔高时,可以选取与塔底在同一水平面内的两个测量基点与.现测得,,,并在点处测得塔顶的仰角.
(Ⅰ)求与两点间的距离;
(Ⅱ)求塔高.
17.(本小题满分15分)
随着全民健身意识增强,马拉松运动逐渐成为深受群众喜爱的体育健身项目之一.吉林市自年以来,现已成功举办五届马拉松比赛,“吉马”也因此成为了东北地区乃至全国颇具影响力的品牌赛事.年“吉马”被中国田径协会评为“城市形象媒体传播赛事典型案例”.时隔一年,吉林市委、市政府再次启动这一国际化赛事,将挑战自我、超越极限、坚韧不拔、永不放弃的马拉松精神与我市激流勇进的城市精神相结合,并将其发扬光大.为此,某校举办了“吉马”知识竞赛,从所有竞赛成绩中抽取一个容量为的样本,并按竞赛成绩(单位:分)分成六组:,,,,,,得到如下图所示的频率分布直方图.
(Ⅰ)求频率分布直方图中的值,并求样本中竞赛成绩的第百分位数;
(Ⅱ)现从样本中竞赛成绩在内用比例分配的分层随机抽样的方法抽取人,再从这人中抽取人座谈,求至少有一人竞赛成绩在内的概率;
(Ⅲ)已知样本中竞赛成绩在内的平均数,方差,样本中竞赛成绩在内的平均数,方差,并据此估计所有答卷中竞赛成绩在内的总体方差.
参考公式:总体分为层,通过分层随机抽样,各层抽取的样本量、样本平均数和样本方差分别为:;.记总的样本平均数为,样本方差为,.
18.(本小题满分17分)
如图,在四棱锥中,,,,且是的中点.
(Ⅰ)求证:平面;
(Ⅱ)若平面平面,且,.
(i)求证:平面;
(ii)求直线与平面所成的角的正弦值.
19.(本小题满分17分)
法国伟大的军事家、政治家拿破仑一生钟爱数学,他发现并证明了著名的拿破仑定理 :“以任意的三角形的三条边为边向外构造三个等边三角形,则这三个等边三角形的中心恰
为另一个等边三角形的顶点”.如图,的内角,,的对边分别为,,,,以,,为边向外作三个等边三角形,其中心分别为,,.
(Ⅰ)求角;
(Ⅱ)若,且的周长为,求;
(Ⅲ)若的面积为,求的角平分线的取值范围.
★ 保密·启用前 ★
高一数学试卷 第1页 (共6页)
同课章节目录
