新疆维吾尔自治区乌鲁木齐市2023-2024学年七年级下学期期末数学试卷(含详细解答)
文档属性
| 名称 | 新疆维吾尔自治区乌鲁木齐市2023-2024学年七年级下学期期末数学试卷(含详细解答) |

|
|
| 格式 | docx | ||
| 文件大小 | 281.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-13 00:00:00 | ||
图片预览



文档简介
新疆维吾尔自治区乌鲁木齐市2023-2024学年七年级(下)期末数学试卷
一、选择题(共9小题,每小题3分,共27分)
1.(3分)若x是9的算术平方根,则x是( )
A.3 B.﹣3 C.9 D.81
2.(3分)下面四个数中,无理数是( )
A.3.14 B. C. D.
3.(3分)下列调查中,最适合用普查的是( )
A.调查全县七年级学生本学期期中考试数学成绩情况
B.为订做校服,了解七年级某班学生的校服尺码
C.调查全市中学生的视力情况
D.调查某品牌圆珠笔笔芯的使用寿命
4.(3分)如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,则∠2的度数为( )
A.35° B.45° C.55° D.125°
5.(3分)若a<b,下列不等式不一定成立的是( )
A.a﹣5<b﹣5 B.﹣5a>﹣5b C. D.a+c<b+c
6.(3分)有下列四个命题:
①相等的角是对顶角;
②两条直线被第三条直线所截,同位角相等;
③无理数包括正无理数、0、负无理数;
④同一平面内,垂直于同一条直线的两条直线平行.
是真命题的命题的个数有( )个.
A.1 B.2 C.3 D.4
7.(3分)如图,数轴上点N表示的数可能是( )
A. B. C. D.
8.(3分)《九章算术》中记载:“今有甲乙二人持钱不知其数,甲得乙半而钱五十,乙得甲太半而钱亦五十.问甲、乙持钱各几何?”其大意是:“今有甲乙二人,不知其钱包里有多少钱,若乙把其一半的钱给甲,则甲的钱数为50;而甲把其的钱给乙,则乙的钱数也能为50,问甲、乙各有多少钱?”设甲的钱数为x,乙的钱数为y,根据题意,可列方程组为( )
A. B.
C. D.
9.(3分)如图,一个质点在第一象限及x轴、y轴上运动,在第一秒钟,它从原点(0,0)运动到(0,1),然后接着按图中箭头所示方向运动,即(0,0)→(0,1)→(1,1)→(1,0)→ ,且每秒移动一个单位长度,那么第99秒时质点所在位置的坐标是( )
A.(9,0) B.(0,9) C.(8,0) D.(0,8)
二.填空题(共6小题。每小题3分,共18分)
10.(3分)如图,把小河里的水引到田地C处,作CD垂直于河岸,沿CD挖水沟,则水沟最短,其理论依据是
11.(3分)若A(2x﹣5,6﹣2x)在第四象限,求x的取值范围 .
12.(3分)如图,直线AB,CD相交于点O,已知∠AOC=75°,OE把∠B0D分成两部分,且∠BOE:∠EOD=3:2,则∠EOD= .
13.(3分)若关于x、y的方程组的解满足x+y=,则m= .
14.(3分)用一根80cm的绳子围成一个长方形,且这个长方形的长比宽多10cm,则围成长方形的面积为 cm2.
15.(3分)对x,y定义一种新的运算,规定,如F(2,1)=2﹣2×1=0,若关于正数m的不等式组恰好有2个整数解,则a的取值范围是 .
二.填空题(共8小题。每小题4分,共18分)
16.(4分)计算:.
17.(5分)解方程组:.
18.(6分)解不等式组,并把解集在数轴上表示出来.
19.(6分)如图,DB平分∠ADC,∠1=∠3.
(1)求证:AB∥DC;
(2)若∠2=55°,求∠A的度数.
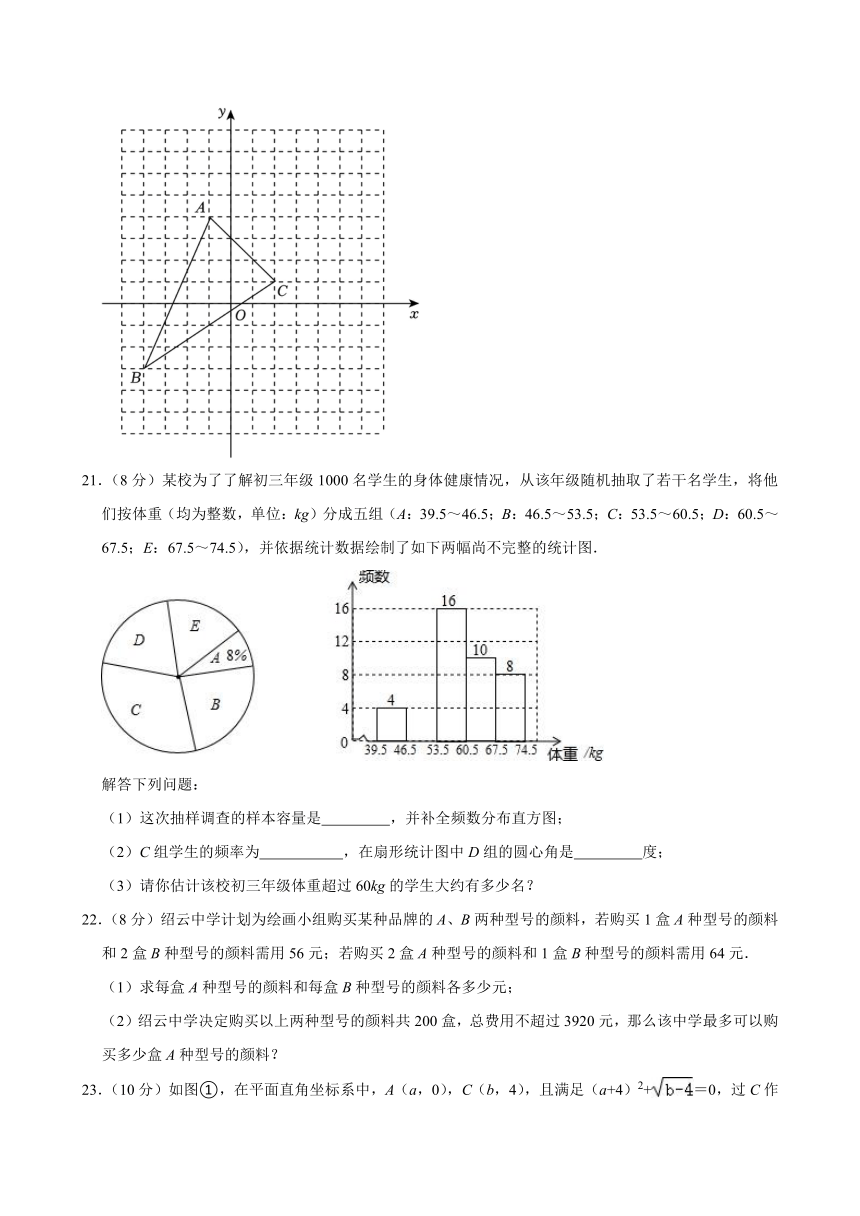
20.(9分)如图,将三角形ABC向右平移5个单位长度,再向上平移3个单位长度,请解答下列问题:
(1)写出点A,B,C的坐标;
(2)画出平移后的三角形A′B′C′;
(3)三角形ABC的面积是 .
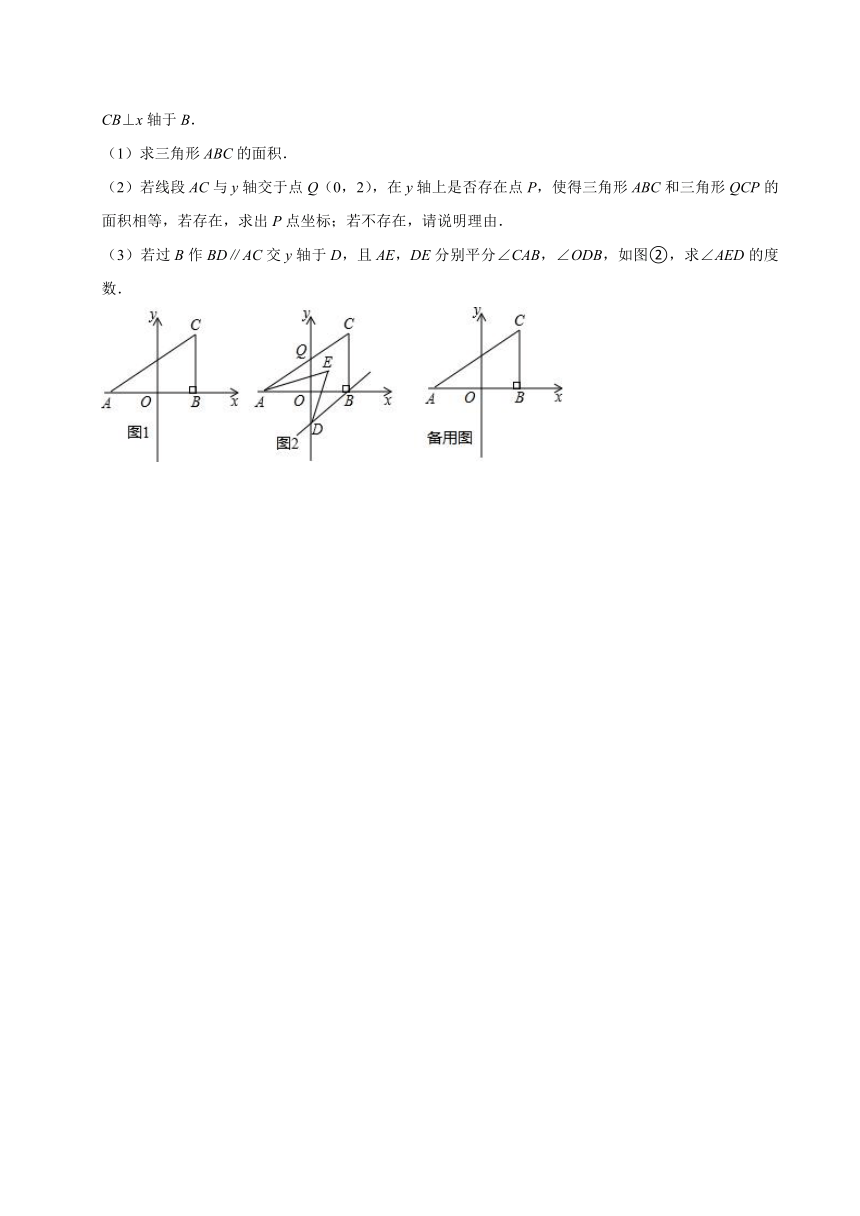
21.(8分)某校为了了解初三年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.
解答下列问题:
(1)这次抽样调查的样本容量是 ,并补全频数分布直方图;
(2)C组学生的频率为 ,在扇形统计图中D组的圆心角是 度;
(3)请你估计该校初三年级体重超过60kg的学生大约有多少名?
22.(8分)绍云中学计划为绘画小组购买某种品牌的A、B两种型号的颜料,若购买1盒A种型号的颜料和2盒B种型号的颜料需用56元;若购买2盒A种型号的颜料和1盒B种型号的颜料需用64元.
(1)求每盒A种型号的颜料和每盒B种型号的颜料各多少元;
(2)绍云中学决定购买以上两种型号的颜料共200盒,总费用不超过3920元,那么该中学最多可以购买多少盒A种型号的颜料?
23.(10分)如图①,在平面直角坐标系中,A(a,0),C(b,4),且满足(a+4)2+=0,过C作CB⊥x轴于B.
(1)求三角形ABC的面积.
(2)若线段AC与y轴交于点Q(0,2),在y轴上是否存在点P,使得三角形ABC和三角形QCP的面积相等,若存在,求出P点坐标;若不存在,请说明理由.
(3)若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,如图②,求∠AED的度数.
参考答案与试题解析
一、选择题(共9小题,每小题3分,共27分)
1.(3分)若x是9的算术平方根,则x是( )
A.3 B.﹣3 C.9 D.81
【解答】解:∵32=9,
∴=3,
故选:A.
2.(3分)下面四个数中,无理数是( )
A.3.14 B. C. D.
【解答】解:3.14是有限小数,是分数,=4是整数,它们不是无理数;
﹣是无限不循环小数,它是无理数;
故选:D.
3.(3分)下列调查中,最适合用普查的是( )
A.调查全县七年级学生本学期期中考试数学成绩情况
B.为订做校服,了解七年级某班学生的校服尺码
C.调查全市中学生的视力情况
D.调查某品牌圆珠笔笔芯的使用寿命
【解答】解:调查全县七年级学生本学期期中考试数学成绩情况,适合用抽样方式,A不合题意;
为订做校服,了解七年级某班学生的校服尺码,适合用普查方式,B符合题意;
调查全市中学生的视力情况,适合用抽样方式,C不合题意;
调查某品牌圆珠笔笔芯的使用寿命,适合用抽样方式,D不合题意;
故选:B.
4.(3分)如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,则∠2的度数为( )
A.35° B.45° C.55° D.125°
【解答】解:∵a∥b,
∴BC与b所夹锐角等于∠1=55°,
又AB⊥BC,
∴∠2=180°﹣90°﹣55°=35°.
故选:A.
5.(3分)若a<b,下列不等式不一定成立的是( )
A.a﹣5<b﹣5 B.﹣5a>﹣5b C. D.a+c<b+c
【解答】解:A、∵a<b,∴a﹣5<b﹣5,故A不符合题意;
B、∵a<b,∴﹣5a>﹣5b,故B不符合题意;
C、∵a<b,c>0,∴<,故C符合题意;
D、∵a<b,∴a+c<b+c,故D不符合题意;
故选:C.
6.(3分)有下列四个命题:
①相等的角是对顶角;
②两条直线被第三条直线所截,同位角相等;
③无理数包括正无理数、0、负无理数;
④同一平面内,垂直于同一条直线的两条直线平行.
是真命题的命题的个数有( )个.
A.1 B.2 C.3 D.4
【解答】解:①相等的角不一定是对顶角,原说法不正确,故不符合题意;
②两条平行线被第三条直线所截,同位角相等,故不符合题意;
③无理数包括正无理数、负无理数,0是有理数,故不符合题意;
④同一平面内,垂直于同一条直线的两条直线平行,所以命题正确;
所以真命题有1个;
故选:A.
7.(3分)如图,数轴上点N表示的数可能是( )
A. B. C. D.
【解答】解:∵N在3和4之间,
∴<N<,
∵﹣<<<,
∴可排除B,C、D.
故选:A.
8.(3分)《九章算术》中记载:“今有甲乙二人持钱不知其数,甲得乙半而钱五十,乙得甲太半而钱亦五十.问甲、乙持钱各几何?”其大意是:“今有甲乙二人,不知其钱包里有多少钱,若乙把其一半的钱给甲,则甲的钱数为50;而甲把其的钱给乙,则乙的钱数也能为50,问甲、乙各有多少钱?”设甲的钱数为x,乙的钱数为y,根据题意,可列方程组为( )
A. B.
C. D.
【解答】解:由题意可得,
,
故选:A.
9.(3分)如图,一个质点在第一象限及x轴、y轴上运动,在第一秒钟,它从原点(0,0)运动到(0,1),然后接着按图中箭头所示方向运动,即(0,0)→(0,1)→(1,1)→(1,0)→ ,且每秒移动一个单位长度,那么第99秒时质点所在位置的坐标是( )
A.(9,0) B.(0,9) C.(8,0) D.(0,8)
【解答】解:由题意可知:
当点移动到(1,1)时,用时2秒,
当点移动到(2,2)时,用时6秒,
当点移动到(3,3)时,用时12秒;
∴点移动到(n,n)时,用的时间为n(n+1)秒,
当点移动到(0,1)时,先向右移动1秒,得到(1,1),再向下移动1秒得到(1,0),
当点移动到(0,2)时,向上移动1秒,得到(0,3),
当点移动到(0,3)时,先向右移动3秒,得到(3,3),再向下移动3秒得到(3,0),
∴当点移动到(0,n)时,n为奇数时,先向右移动n秒,得到(n,n),再向下移动n秒,得到(n,0),n为偶数时,向上移动1秒,得到(0,n+1),
∴当点移动到(9,9)时,用时9×10=90秒,再向下移动9秒,得到(9,0),
即:第99秒时质点所在位置的坐标是为(9,0);
故选:A.
二.填空题(共6小题。每小题3分,共18分)
10.(3分)如图,把小河里的水引到田地C处,作CD垂直于河岸,沿CD挖水沟,则水沟最短,其理论依据是 垂线段最短
【解答】解:其依据是:连接直线外一点与直线上各点的所有线段中,垂线段最短.
故答案为:垂线段最短.
11.(3分)若A(2x﹣5,6﹣2x)在第四象限,求x的取值范围 x>3 .
【解答】解:∵A(2x﹣5,6﹣2x)在第四象限,
∴,
解得x>3.
故答案为x>3.
12.(3分)如图,直线AB,CD相交于点O,已知∠AOC=75°,OE把∠B0D分成两部分,且∠BOE:∠EOD=3:2,则∠EOD= 30° .
【解答】解:∵∠AOC=75°,
∴∠BOD=∠AOC=75°,
∵∠BOE:∠EOD=3:2,
∴∠BOE=45°,∠EOD=30°,
故答案为:30°.
13.(3分)若关于x、y的方程组的解满足x+y=,则m= 1 .
【解答】解:,
①+②得:5(x+y)=2m+1,
解得:x+y=,
代入已知等式得:=,
解得:m=1.
故答案为:1.
14.(3分)用一根80cm的绳子围成一个长方形,且这个长方形的长比宽多10cm,则围成长方形的面积为 375 cm2.
【解答】解:设长方形的宽为x cm,则长方形的长为(x+10)cm,
依题意得:2(x+10+x)=80,
解得:x=15,
∴(x+10) x=(15+10)×15=375,
即围成长方形的面积为375cm2.
故答案为:375.
15.(3分)对x,y定义一种新的运算,规定,如F(2,1)=2﹣2×1=0,若关于正数m的不等式组恰好有2个整数解,则a的取值范围是 4≤a<5 .
【解答】解:由题意,∵3>1,m>0,
∴3m>m.
∴F(3m,m)=3m﹣2m=m.
∵﹣3<﹣2,m>0,
∴﹣3m<﹣2m.
∴﹣1﹣3m<﹣3m<﹣2m.
∴F(﹣1﹣3m,﹣2m)=﹣2m﹣(﹣1﹣3m)=m+1.
∴原不等式组可以化为.
∴原不等式组的解集为1<m≤a﹣1.
∵原不等式组恰好有2个整数解,
∴3≤a﹣1<4.
∴4≤a<5.
二.填空题(共8小题。每小题4分,共18分)
16.(4分)计算:.
【解答】解:原式=﹣1+3﹣2
=.
17.(5分)解方程组:.
【解答】解:,
①×3,得6x+3y=15,③
②+③,得7x=21,
x=3.
把x=3代入①,得2×3+y=5,
y=﹣1.
∴原方程组的解是.
18.(6分)解不等式组,并把解集在数轴上表示出来.
【解答】解:,
解不等式①得:x>﹣,
解不等式②得:x≤5,
∴不等式组的解集为:﹣<x≤5,
在数轴上表示不等式组的解集为:
.
19.(6分)如图,DB平分∠ADC,∠1=∠3.
(1)求证:AB∥DC;
(2)若∠2=55°,求∠A的度数.
【解答】解:(1)∵DB平分∠ADC,
∴∠1=∠2,
又∵∠1=∠3,
∴∠2=∠3,
∴AB∥CD;
(2)∵DB平分∠ADC,
∴∠ADC=2∠2=2×55°=110°,
又∵AB∥CD,
∴∠A+∠ADC=180°,
∴∠A=180°﹣∠ADC,
=180°﹣110°
=70°.
20.(9分)如图,将三角形ABC向右平移5个单位长度,再向上平移3个单位长度,请解答下列问题:
(1)写出点A,B,C的坐标;
(2)画出平移后的三角形A′B′C′;
(3)三角形ABC的面积是 15 .
【解答】解:(1)A(﹣1,4),B(﹣4,﹣3),C(2,1);
(2)如图,△A′B′C′即为所求;
(3)△ABC的面积=6×7﹣×3×7﹣×3×3﹣×6×4=15.
故答案为:15.
21.(8分)某校为了了解初三年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.
解答下列问题:
(1)这次抽样调查的样本容量是 50 ,并补全频数分布直方图;
(2)C组学生的频率为 0.32 ,在扇形统计图中D组的圆心角是 72 度;
(3)请你估计该校初三年级体重超过60kg的学生大约有多少名?
【解答】解:(1)这次抽样调查的样本容量是4÷8%=50,B组的频数=50﹣4﹣16﹣10﹣8=12,
补全频数分布直方图,如图:
(2)C组学生的频率是0.32;D组的圆心角=;
(3)样本中体重超过60kg的学生是10+8=18(人),
该校初三年级体重超过60kg的学生大约=(人),
故答案为:(1)50;(2)0.32;72.
22.(8分)绍云中学计划为绘画小组购买某种品牌的A、B两种型号的颜料,若购买1盒A种型号的颜料和2盒B种型号的颜料需用56元;若购买2盒A种型号的颜料和1盒B种型号的颜料需用64元.
(1)求每盒A种型号的颜料和每盒B种型号的颜料各多少元;
(2)绍云中学决定购买以上两种型号的颜料共200盒,总费用不超过3920元,那么该中学最多可以购买多少盒A种型号的颜料?
【解答】解:(1)设每盒A种型号的颜料x元,每盒B种型号的颜料y元,
依题意得:,
解得:.
答:每盒A种型号的颜料24元,每盒B种型号的颜料16元.
(2)设该中学可以购买m盒A种型号的颜料,则可以购买(200﹣m)盒B种型号的颜料,
依题意得:24m+16(200﹣m)≤3920,
解得:m≤90.
答:该中学最多可以购买90盒A种型号的颜料.
23.(10分)如图①,在平面直角坐标系中,A(a,0),C(b,4),且满足(a+4)2+=0,过C作CB⊥x轴于B.
(1)求三角形ABC的面积.
(2)若线段AC与y轴交于点Q(0,2),在y轴上是否存在点P,使得三角形ABC和三角形QCP的面积相等,若存在,求出P点坐标;若不存在,请说明理由.
(3)若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,如图②,求∠AED的度数.
【解答】解:(1)∵(a+4)2+=0,
又∵(a+4)2+≥0,≥0
∴,
∴,
∴A(﹣4,0),C(4,4),B(4,0),
∴S△ABC= AB BC=×8×4=16.
(2)设P点坐标为(0,y),
∵Q(0,2),
∴PQ=|y﹣2|,
当S△PQC=S△ABC=16时,
|y﹣2|×4=16,
解得y=10或﹣6,
∴P(0,10)或(0,﹣6).
(3)如图2中:过点E作EF∥AC,
∵AC∥BD
∴EF∥BD
∴∠CAE=∠AEF,∠EDB=∠DEF
∴∠CAE+∠EDB=∠AEF+∠DEF
∴∠AED=∠CAE+∠BDE
∵AE、DE分别平分∠CAB和∠ODB
∴∠CAE=∠CAB,∠BDE=∠ODB,
∵AC∥BD
∴∠ODB=∠AQD
∴∠AED=(∠CAB+∠ODB)=(∠CAB+∠AQD)=×90°=45°.
一、选择题(共9小题,每小题3分,共27分)
1.(3分)若x是9的算术平方根,则x是( )
A.3 B.﹣3 C.9 D.81
2.(3分)下面四个数中,无理数是( )
A.3.14 B. C. D.
3.(3分)下列调查中,最适合用普查的是( )
A.调查全县七年级学生本学期期中考试数学成绩情况
B.为订做校服,了解七年级某班学生的校服尺码
C.调查全市中学生的视力情况
D.调查某品牌圆珠笔笔芯的使用寿命
4.(3分)如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,则∠2的度数为( )
A.35° B.45° C.55° D.125°
5.(3分)若a<b,下列不等式不一定成立的是( )
A.a﹣5<b﹣5 B.﹣5a>﹣5b C. D.a+c<b+c
6.(3分)有下列四个命题:
①相等的角是对顶角;
②两条直线被第三条直线所截,同位角相等;
③无理数包括正无理数、0、负无理数;
④同一平面内,垂直于同一条直线的两条直线平行.
是真命题的命题的个数有( )个.
A.1 B.2 C.3 D.4
7.(3分)如图,数轴上点N表示的数可能是( )
A. B. C. D.
8.(3分)《九章算术》中记载:“今有甲乙二人持钱不知其数,甲得乙半而钱五十,乙得甲太半而钱亦五十.问甲、乙持钱各几何?”其大意是:“今有甲乙二人,不知其钱包里有多少钱,若乙把其一半的钱给甲,则甲的钱数为50;而甲把其的钱给乙,则乙的钱数也能为50,问甲、乙各有多少钱?”设甲的钱数为x,乙的钱数为y,根据题意,可列方程组为( )
A. B.
C. D.
9.(3分)如图,一个质点在第一象限及x轴、y轴上运动,在第一秒钟,它从原点(0,0)运动到(0,1),然后接着按图中箭头所示方向运动,即(0,0)→(0,1)→(1,1)→(1,0)→ ,且每秒移动一个单位长度,那么第99秒时质点所在位置的坐标是( )
A.(9,0) B.(0,9) C.(8,0) D.(0,8)
二.填空题(共6小题。每小题3分,共18分)
10.(3分)如图,把小河里的水引到田地C处,作CD垂直于河岸,沿CD挖水沟,则水沟最短,其理论依据是
11.(3分)若A(2x﹣5,6﹣2x)在第四象限,求x的取值范围 .
12.(3分)如图,直线AB,CD相交于点O,已知∠AOC=75°,OE把∠B0D分成两部分,且∠BOE:∠EOD=3:2,则∠EOD= .
13.(3分)若关于x、y的方程组的解满足x+y=,则m= .
14.(3分)用一根80cm的绳子围成一个长方形,且这个长方形的长比宽多10cm,则围成长方形的面积为 cm2.
15.(3分)对x,y定义一种新的运算,规定,如F(2,1)=2﹣2×1=0,若关于正数m的不等式组恰好有2个整数解,则a的取值范围是 .
二.填空题(共8小题。每小题4分,共18分)
16.(4分)计算:.
17.(5分)解方程组:.
18.(6分)解不等式组,并把解集在数轴上表示出来.
19.(6分)如图,DB平分∠ADC,∠1=∠3.
(1)求证:AB∥DC;
(2)若∠2=55°,求∠A的度数.
20.(9分)如图,将三角形ABC向右平移5个单位长度,再向上平移3个单位长度,请解答下列问题:
(1)写出点A,B,C的坐标;
(2)画出平移后的三角形A′B′C′;
(3)三角形ABC的面积是 .
21.(8分)某校为了了解初三年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.
解答下列问题:
(1)这次抽样调查的样本容量是 ,并补全频数分布直方图;
(2)C组学生的频率为 ,在扇形统计图中D组的圆心角是 度;
(3)请你估计该校初三年级体重超过60kg的学生大约有多少名?
22.(8分)绍云中学计划为绘画小组购买某种品牌的A、B两种型号的颜料,若购买1盒A种型号的颜料和2盒B种型号的颜料需用56元;若购买2盒A种型号的颜料和1盒B种型号的颜料需用64元.
(1)求每盒A种型号的颜料和每盒B种型号的颜料各多少元;
(2)绍云中学决定购买以上两种型号的颜料共200盒,总费用不超过3920元,那么该中学最多可以购买多少盒A种型号的颜料?
23.(10分)如图①,在平面直角坐标系中,A(a,0),C(b,4),且满足(a+4)2+=0,过C作CB⊥x轴于B.
(1)求三角形ABC的面积.
(2)若线段AC与y轴交于点Q(0,2),在y轴上是否存在点P,使得三角形ABC和三角形QCP的面积相等,若存在,求出P点坐标;若不存在,请说明理由.
(3)若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,如图②,求∠AED的度数.
参考答案与试题解析
一、选择题(共9小题,每小题3分,共27分)
1.(3分)若x是9的算术平方根,则x是( )
A.3 B.﹣3 C.9 D.81
【解答】解:∵32=9,
∴=3,
故选:A.
2.(3分)下面四个数中,无理数是( )
A.3.14 B. C. D.
【解答】解:3.14是有限小数,是分数,=4是整数,它们不是无理数;
﹣是无限不循环小数,它是无理数;
故选:D.
3.(3分)下列调查中,最适合用普查的是( )
A.调查全县七年级学生本学期期中考试数学成绩情况
B.为订做校服,了解七年级某班学生的校服尺码
C.调查全市中学生的视力情况
D.调查某品牌圆珠笔笔芯的使用寿命
【解答】解:调查全县七年级学生本学期期中考试数学成绩情况,适合用抽样方式,A不合题意;
为订做校服,了解七年级某班学生的校服尺码,适合用普查方式,B符合题意;
调查全市中学生的视力情况,适合用抽样方式,C不合题意;
调查某品牌圆珠笔笔芯的使用寿命,适合用抽样方式,D不合题意;
故选:B.
4.(3分)如图,直线a∥b,点B在直线b上,且AB⊥BC,∠1=55°,则∠2的度数为( )
A.35° B.45° C.55° D.125°
【解答】解:∵a∥b,
∴BC与b所夹锐角等于∠1=55°,
又AB⊥BC,
∴∠2=180°﹣90°﹣55°=35°.
故选:A.
5.(3分)若a<b,下列不等式不一定成立的是( )
A.a﹣5<b﹣5 B.﹣5a>﹣5b C. D.a+c<b+c
【解答】解:A、∵a<b,∴a﹣5<b﹣5,故A不符合题意;
B、∵a<b,∴﹣5a>﹣5b,故B不符合题意;
C、∵a<b,c>0,∴<,故C符合题意;
D、∵a<b,∴a+c<b+c,故D不符合题意;
故选:C.
6.(3分)有下列四个命题:
①相等的角是对顶角;
②两条直线被第三条直线所截,同位角相等;
③无理数包括正无理数、0、负无理数;
④同一平面内,垂直于同一条直线的两条直线平行.
是真命题的命题的个数有( )个.
A.1 B.2 C.3 D.4
【解答】解:①相等的角不一定是对顶角,原说法不正确,故不符合题意;
②两条平行线被第三条直线所截,同位角相等,故不符合题意;
③无理数包括正无理数、负无理数,0是有理数,故不符合题意;
④同一平面内,垂直于同一条直线的两条直线平行,所以命题正确;
所以真命题有1个;
故选:A.
7.(3分)如图,数轴上点N表示的数可能是( )
A. B. C. D.
【解答】解:∵N在3和4之间,
∴<N<,
∵﹣<<<,
∴可排除B,C、D.
故选:A.
8.(3分)《九章算术》中记载:“今有甲乙二人持钱不知其数,甲得乙半而钱五十,乙得甲太半而钱亦五十.问甲、乙持钱各几何?”其大意是:“今有甲乙二人,不知其钱包里有多少钱,若乙把其一半的钱给甲,则甲的钱数为50;而甲把其的钱给乙,则乙的钱数也能为50,问甲、乙各有多少钱?”设甲的钱数为x,乙的钱数为y,根据题意,可列方程组为( )
A. B.
C. D.
【解答】解:由题意可得,
,
故选:A.
9.(3分)如图,一个质点在第一象限及x轴、y轴上运动,在第一秒钟,它从原点(0,0)运动到(0,1),然后接着按图中箭头所示方向运动,即(0,0)→(0,1)→(1,1)→(1,0)→ ,且每秒移动一个单位长度,那么第99秒时质点所在位置的坐标是( )
A.(9,0) B.(0,9) C.(8,0) D.(0,8)
【解答】解:由题意可知:
当点移动到(1,1)时,用时2秒,
当点移动到(2,2)时,用时6秒,
当点移动到(3,3)时,用时12秒;
∴点移动到(n,n)时,用的时间为n(n+1)秒,
当点移动到(0,1)时,先向右移动1秒,得到(1,1),再向下移动1秒得到(1,0),
当点移动到(0,2)时,向上移动1秒,得到(0,3),
当点移动到(0,3)时,先向右移动3秒,得到(3,3),再向下移动3秒得到(3,0),
∴当点移动到(0,n)时,n为奇数时,先向右移动n秒,得到(n,n),再向下移动n秒,得到(n,0),n为偶数时,向上移动1秒,得到(0,n+1),
∴当点移动到(9,9)时,用时9×10=90秒,再向下移动9秒,得到(9,0),
即:第99秒时质点所在位置的坐标是为(9,0);
故选:A.
二.填空题(共6小题。每小题3分,共18分)
10.(3分)如图,把小河里的水引到田地C处,作CD垂直于河岸,沿CD挖水沟,则水沟最短,其理论依据是 垂线段最短
【解答】解:其依据是:连接直线外一点与直线上各点的所有线段中,垂线段最短.
故答案为:垂线段最短.
11.(3分)若A(2x﹣5,6﹣2x)在第四象限,求x的取值范围 x>3 .
【解答】解:∵A(2x﹣5,6﹣2x)在第四象限,
∴,
解得x>3.
故答案为x>3.
12.(3分)如图,直线AB,CD相交于点O,已知∠AOC=75°,OE把∠B0D分成两部分,且∠BOE:∠EOD=3:2,则∠EOD= 30° .
【解答】解:∵∠AOC=75°,
∴∠BOD=∠AOC=75°,
∵∠BOE:∠EOD=3:2,
∴∠BOE=45°,∠EOD=30°,
故答案为:30°.
13.(3分)若关于x、y的方程组的解满足x+y=,则m= 1 .
【解答】解:,
①+②得:5(x+y)=2m+1,
解得:x+y=,
代入已知等式得:=,
解得:m=1.
故答案为:1.
14.(3分)用一根80cm的绳子围成一个长方形,且这个长方形的长比宽多10cm,则围成长方形的面积为 375 cm2.
【解答】解:设长方形的宽为x cm,则长方形的长为(x+10)cm,
依题意得:2(x+10+x)=80,
解得:x=15,
∴(x+10) x=(15+10)×15=375,
即围成长方形的面积为375cm2.
故答案为:375.
15.(3分)对x,y定义一种新的运算,规定,如F(2,1)=2﹣2×1=0,若关于正数m的不等式组恰好有2个整数解,则a的取值范围是 4≤a<5 .
【解答】解:由题意,∵3>1,m>0,
∴3m>m.
∴F(3m,m)=3m﹣2m=m.
∵﹣3<﹣2,m>0,
∴﹣3m<﹣2m.
∴﹣1﹣3m<﹣3m<﹣2m.
∴F(﹣1﹣3m,﹣2m)=﹣2m﹣(﹣1﹣3m)=m+1.
∴原不等式组可以化为.
∴原不等式组的解集为1<m≤a﹣1.
∵原不等式组恰好有2个整数解,
∴3≤a﹣1<4.
∴4≤a<5.
二.填空题(共8小题。每小题4分,共18分)
16.(4分)计算:.
【解答】解:原式=﹣1+3﹣2
=.
17.(5分)解方程组:.
【解答】解:,
①×3,得6x+3y=15,③
②+③,得7x=21,
x=3.
把x=3代入①,得2×3+y=5,
y=﹣1.
∴原方程组的解是.
18.(6分)解不等式组,并把解集在数轴上表示出来.
【解答】解:,
解不等式①得:x>﹣,
解不等式②得:x≤5,
∴不等式组的解集为:﹣<x≤5,
在数轴上表示不等式组的解集为:
.
19.(6分)如图,DB平分∠ADC,∠1=∠3.
(1)求证:AB∥DC;
(2)若∠2=55°,求∠A的度数.
【解答】解:(1)∵DB平分∠ADC,
∴∠1=∠2,
又∵∠1=∠3,
∴∠2=∠3,
∴AB∥CD;
(2)∵DB平分∠ADC,
∴∠ADC=2∠2=2×55°=110°,
又∵AB∥CD,
∴∠A+∠ADC=180°,
∴∠A=180°﹣∠ADC,
=180°﹣110°
=70°.
20.(9分)如图,将三角形ABC向右平移5个单位长度,再向上平移3个单位长度,请解答下列问题:
(1)写出点A,B,C的坐标;
(2)画出平移后的三角形A′B′C′;
(3)三角形ABC的面积是 15 .
【解答】解:(1)A(﹣1,4),B(﹣4,﹣3),C(2,1);
(2)如图,△A′B′C′即为所求;
(3)△ABC的面积=6×7﹣×3×7﹣×3×3﹣×6×4=15.
故答案为:15.
21.(8分)某校为了了解初三年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.
解答下列问题:
(1)这次抽样调查的样本容量是 50 ,并补全频数分布直方图;
(2)C组学生的频率为 0.32 ,在扇形统计图中D组的圆心角是 72 度;
(3)请你估计该校初三年级体重超过60kg的学生大约有多少名?
【解答】解:(1)这次抽样调查的样本容量是4÷8%=50,B组的频数=50﹣4﹣16﹣10﹣8=12,
补全频数分布直方图,如图:
(2)C组学生的频率是0.32;D组的圆心角=;
(3)样本中体重超过60kg的学生是10+8=18(人),
该校初三年级体重超过60kg的学生大约=(人),
故答案为:(1)50;(2)0.32;72.
22.(8分)绍云中学计划为绘画小组购买某种品牌的A、B两种型号的颜料,若购买1盒A种型号的颜料和2盒B种型号的颜料需用56元;若购买2盒A种型号的颜料和1盒B种型号的颜料需用64元.
(1)求每盒A种型号的颜料和每盒B种型号的颜料各多少元;
(2)绍云中学决定购买以上两种型号的颜料共200盒,总费用不超过3920元,那么该中学最多可以购买多少盒A种型号的颜料?
【解答】解:(1)设每盒A种型号的颜料x元,每盒B种型号的颜料y元,
依题意得:,
解得:.
答:每盒A种型号的颜料24元,每盒B种型号的颜料16元.
(2)设该中学可以购买m盒A种型号的颜料,则可以购买(200﹣m)盒B种型号的颜料,
依题意得:24m+16(200﹣m)≤3920,
解得:m≤90.
答:该中学最多可以购买90盒A种型号的颜料.
23.(10分)如图①,在平面直角坐标系中,A(a,0),C(b,4),且满足(a+4)2+=0,过C作CB⊥x轴于B.
(1)求三角形ABC的面积.
(2)若线段AC与y轴交于点Q(0,2),在y轴上是否存在点P,使得三角形ABC和三角形QCP的面积相等,若存在,求出P点坐标;若不存在,请说明理由.
(3)若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,如图②,求∠AED的度数.
【解答】解:(1)∵(a+4)2+=0,
又∵(a+4)2+≥0,≥0
∴,
∴,
∴A(﹣4,0),C(4,4),B(4,0),
∴S△ABC= AB BC=×8×4=16.
(2)设P点坐标为(0,y),
∵Q(0,2),
∴PQ=|y﹣2|,
当S△PQC=S△ABC=16时,
|y﹣2|×4=16,
解得y=10或﹣6,
∴P(0,10)或(0,﹣6).
(3)如图2中:过点E作EF∥AC,
∵AC∥BD
∴EF∥BD
∴∠CAE=∠AEF,∠EDB=∠DEF
∴∠CAE+∠EDB=∠AEF+∠DEF
∴∠AED=∠CAE+∠BDE
∵AE、DE分别平分∠CAB和∠ODB
∴∠CAE=∠CAB,∠BDE=∠ODB,
∵AC∥BD
∴∠ODB=∠AQD
∴∠AED=(∠CAB+∠ODB)=(∠CAB+∠AQD)=×90°=45°.
同课章节目录
