22.3 实际问题与二次函数 专题练习(无答案) 2024—2025学年人教版数学九年级上册
文档属性
| 名称 | 22.3 实际问题与二次函数 专题练习(无答案) 2024—2025学年人教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 426.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-13 16:09:51 | ||
图片预览


文档简介
22.3 实际问题与二次函数 专题练习
1.某工厂计划从现在开始,在每个生产周期内生产并销售完某型号设备,该设备的生产成本为10万元件.设第个生产周期设备的售价为万元/件,售价与之间的函数解析式是,其中是正整数.当时,;当时,.
(1)求,的值:
(2)设第个生产周期生产并销售完设备的数量为件,且与满足关系式.则工厂第几个生产周期获得的利润最大?最大的利润是多少万元?
2.一次足球训练中,小华从球门正前方的A处射门,足球射向球门的运行路线呈抛物线,当球飞行的水平距离为时,球达到最高点,此时球离地面.已知球门高OB为,现以O为原点建立如图所示直角坐标系.
(1)求出抛物线的函数解析式并说明此次射门在不受干扰的情况下能否进球;
(2)若防守队员小明跳起后能摸到的最大高度为2.25米,他此时站在离球门3米远的位置,求小明至少后退多少米才能防守住这次射门?
(3)在射门路线的形状、最大高度均保持不变情况下,适当靠近球门进球的把握会更大,小华决定将足球向球门方向移动一定距离后再射门,他最多可以向球门移动__________.(填序号即可,)
①; ②; ③.
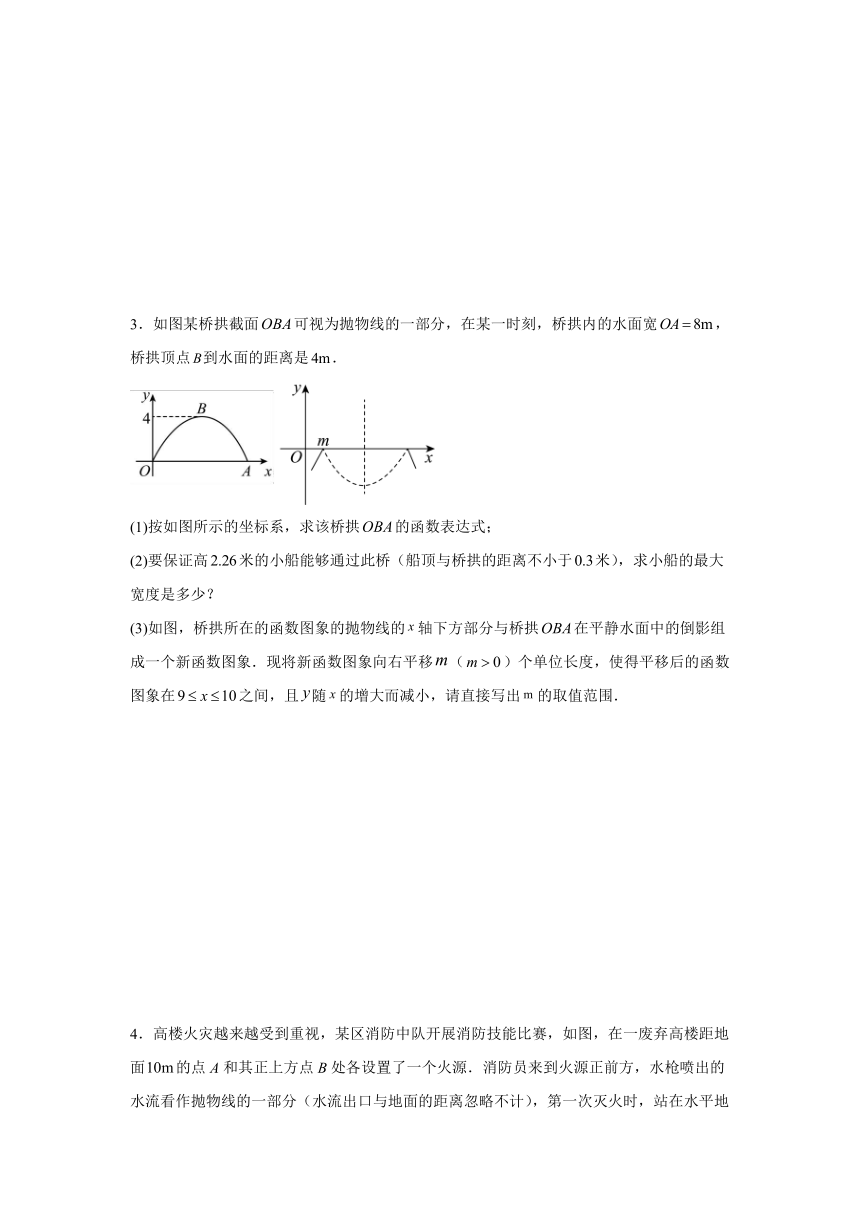
3.如图某桥拱截面可视为抛物线的一部分,在某一时刻,桥拱内的水面宽,桥拱顶点到水面的距离是.
(1)按如图所示的坐标系,求该桥拱的函数表达式;
(2)要保证高米的小船能够通过此桥(船顶与桥拱的距离不小于米),求小船的最大宽度是多少?
(3)如图,桥拱所在的函数图象的抛物线的轴下方部分与桥拱在平静水面中的倒影组成一个新函数图象.现将新函数图象向右平移()个单位长度,使得平移后的函数图象在之间,且随的增大而减小,请直接写出的取值范围.
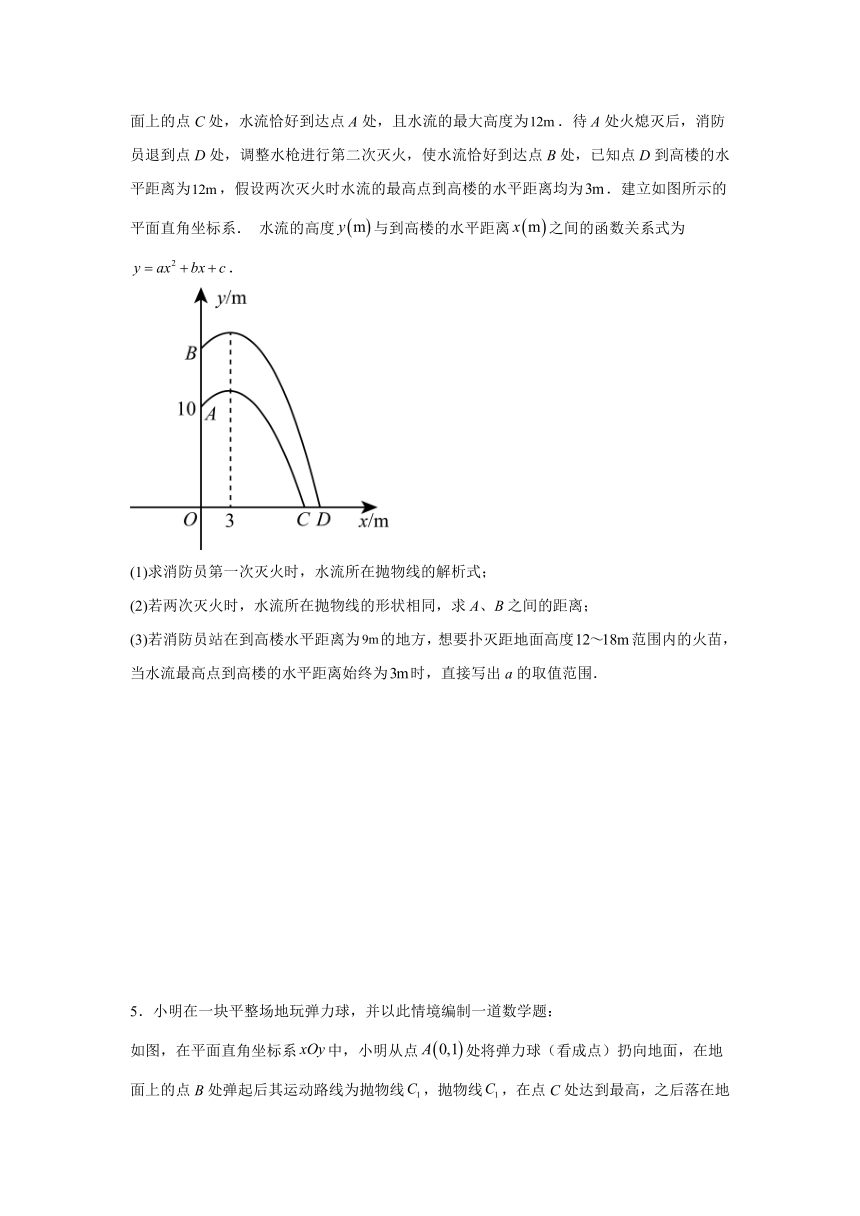
4.高楼火灾越来越受到重视,某区消防中队开展消防技能比赛,如图,在一废弃高楼距地面的点A和其正上方点B处各设置了一个火源.消防员来到火源正前方,水枪喷出的水流看作抛物线的一部分(水流出口与地面的距离忽略不计),第一次灭火时,站在水平地面上的点C处,水流恰好到达点A处,且水流的最大高度为.待A处火熄灭后,消防员退到点D处,调整水枪进行第二次灭火,使水流恰好到达点B处,已知点D到高楼的水平距离为,假设两次灭火时水流的最高点到高楼的水平距离均为.建立如图所示的平面直角坐标系. 水流的高度与到高楼的水平距离之间的函数关系式为.
(1)求消防员第一次灭火时,水流所在抛物线的解析式;
(2)若两次灭火时,水流所在抛物线的形状相同,求A、B之间的距离;
(3)若消防员站在到高楼水平距离为的地方,想要扑灭距地面高度范围内的火苗,当水流最高点到高楼的水平距离始终为时,直接写出a的取值范围.
5.小明在一块平整场地玩弹力球,并以此情境编制一道数学题:
如图,在平面直角坐标系中,小明从点处将弹力球(看成点)扔向地面,在地面上的点B处弹起后其运动路线为抛物线,抛物线,在点C处达到最高,之后落在地面上的点D处,已知,点C坐标为.
(1)求抛物线的表达式及点D坐标;
(2)弹力球在点D处再次弹起,其运动路线为抛物线,抛物线与的形状一致且在E处最高,点E与点O的水平距离为,
①求抛物线与最高点的高度差;
②有一竖直放置的隔板高,且,若弹力球沿C下落过程中要落在隔板上(含端点),其他条件都不变的情况下,需要将起弹点B右移n米,直接写出n的取值范围.
6.一条河上横跨着一座宏伟壮观的悬索桥.桥梁的缆索与缆索均呈抛物线型,桥塔与桥塔均垂直于桥面,如图所示,以O为原点,以直线为x轴,以桥塔所在直线为y轴,建立平面直角坐标系.
已知:缆索所在抛物线与缆索所在抛物线关于y轴对称,桥塔与桥塔之间的距离,,缆索的最低点P到的距离(桥塔的粗细忽略不计)
(1)求缆索所在抛物线的函数表达式;
(2)点E在缆索上,,且,,求的长.
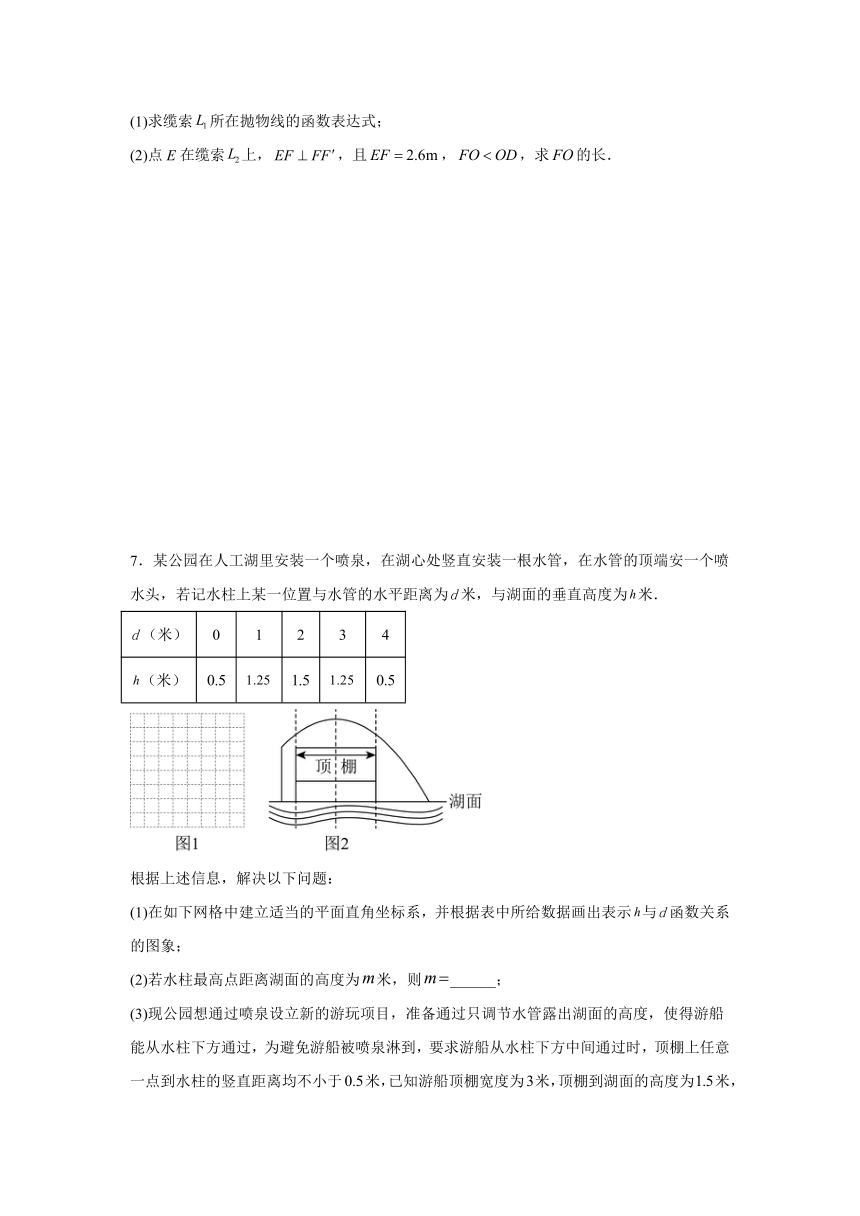
7.某公园在人工湖里安装一个喷泉,在湖心处竖直安装一根水管,在水管的顶端安一个喷水头,若记水柱上某一位置与水管的水平距离为米,与湖面的垂直高度为米.
(米) 0 1 2 3 4
(米)
根据上述信息,解决以下问题:
(1)在如下网格中建立适当的平面直角坐标系,并根据表中所给数据画出表示与函数关系的图象;
(2)若水柱最高点距离湖面的高度为米,则______;
(3)现公园想通过喷泉设立新的游玩项目,准备通过只调节水管露出湖面的高度,使得游船能从水柱下方通过,为避免游船被喷泉淋到,要求游船从水柱下方中间通过时,顶棚上任意一点到水柱的竖直距离均不小于米,已知游船顶棚宽度为米,顶棚到湖面的高度为米,那么公园应将水管露出湖面的高度(喷水头忽略不计)至少调节到多少米才能符合要求.(结果保留一位小数).
8.某课外科技小组制作了一架航模飞机,计划参加学校举办的航模比赛.通过试验;收集了该飞机相对于出发点飞行的水平距离(单位:)、飞行高度(单位:)随飞行时间(单位:)变化的数据,如下表所示:
飞行时间 0 2 4 6 8
飞行水平距离 0 8 16 24 32
飞行高度 0 18 32 42 48
已知与满足一次函数关系,即,与满足二次函数关系.
(1)求关于的函数解析式.(不必写出自变量的取值范围)
(2)如图,活动小组在水平安全线上的点处设置一个起飞平台试飞该航模飞机(平台的高度忽略不计).
①求飞机落到水平安全线时飞行的水平距离.
②若航模比赛规定,以该起飞平台为起点,参赛选手需要控制航模飞机在飞行水平距离为的范围内进行特技动作展示,且动作展示时飞行高度不能低于,请你判断该航模飞机此次试飞能否达到要求,并说明理由.
9.为了解新建道路的通行能力,查阅资料获知:在某种情况下,车流速度V(单位:千米/时)是车流密度x(单位:辆/千米)的函数,其函数图象如图所示.
(1)当时,求V关于x的函数表达式.
(2)车流量是单位时间内通过观测点的车辆数,计算公式为:车流量车流速度车流密度.若车流速度V不超过80千米/时,求当车流密度x为多少时,车流量P(单位:辆/时)达到最大,并求出这一最大值.
10.2024年“五一”假期期间,阆中古城景区某特产店销售A,B两类特产.A类特产进价50元/件,B类特产进价60元/件.已知购买1件A类特产和1件B类特产需132元,购买3件A类特产和5件B类特产需540元.
(1)求A类特产和B类特产每件的售价各是多少元?
(2)A类特产供货充足,按原价销售每天可售出60件.市场调查反映,若每降价1元,每天可多售出10件(每件售价不低于进价).设每件A类特产降价x元,每天的销售量为y件,求y与x的函数关系式,并写出自变量x的取值范围.
(3)在(2)的条件下,由于B类特产供货紧张,每天只能购进100件且能按原价售完.设该店每天销售这两类特产的总利润为w元,求w与x的函数关系式,并求出每件A类特产降价多少元时总利润w最大,最大利润是多少元?(利润=售价-进价)
11.人勤春来早,奋进正当时.眼下正是温室大棚育苗的好时节,大棚种植户开始了新一年的辛勤劳作,在新的一年播下希望的种子.如图是小颖爸爸在屋侧的菜地上搭建的一抛物线型蔬菜大棚,其中一端固定在离水平地面高3米的墙体A处(墙高大于4米),另一端固定在地面上的C点处,现分别以地面和墙体为x轴和y轴建立平面直角坐标系,已知大棚的高度y(米)与大棚离墙体的水平距离x(米)之间的关系式用表示,抛物线的顶点B的横坐标为2.
请根据以上信息,解答下列问题:
(1)求抛物线的函数表达式;
(2)小颖的爸爸准备在抛物线上取一点P(不与A,C重合),安装一直角形钢架对大棚进行加固(点D、E分别在y轴,x轴上,且轴,轴),小颖为爸爸设计了两种方案:
方案一:如图1,将点P设在抛物线的顶点B处,安装直角形钢架对大棚进行加固;
方案二:如图2,将点P设在到墙的水平距离为5米的抛物线上,安装直角形钢架对大棚进行加固.
方案一、二中钢架DPE所需钢材长度分别记为、,请通过计算说明哪种方案更省钢材?(忽略接口处的材料损耗)
12.芯片行业是制约我国工业发展的主要技术之一.经过大量科研、技术人员艰苦攻关,我国芯片有了新突破.某芯片实现国产化后,芯片价格大幅下降.原来每片芯片的单价为元,准备进行两次降价,如果每次降价的百分率都为,经过两次降价后的价格为(元).
(1)求与之间的函数关系式;
(2)如果该芯片经过两次降价后每片芯片单价为元,求每次降价的百分率.
13.如图,二次函数的图像交x轴于A,两点,交y轴于.
(1)求这个二次函数的解析式.
(2)点M为这个二次函数图像上一个动点,点N为坐标平面上任意一点,设点M的横坐标为m,则点N的横坐标为,且轴.
①若点N也在二次函数的图像上,求m的值;
②当线段与二次函数的图像有两个公共点时,请直接写出m的取值范围.
14.如图,某农户计划用篱笆围成一个矩形场地养殖家禽,为充分利用现有资源,该矩形场地一面靠墙(墙的长度为),另外三面用篱笆围成,中间再用篱笆把它分成三个面积相等的矩形分别养殖不同的家禽,计划购买篱笆的总长度为,设矩形场地的长为, 宽为, 面积为.
(1)分别求出y与x,s与x的函数解析式;
(2)当x为何值时,矩形场地的总面积最大?最大面积为多少?
(3)若购买的篱笆总长增加,矩形场地的最大总面积能否达到 若能,请求出x的值;若不能,请说明理由.
15.为有力有效推进乡村全面振兴,在驻村工作队的帮扶下,某村积极推动“合作社+农户”模式托起村民致富梦.村合作社推广种植某特色农产品,每千克成本为20元,规定每千克售价需超过成本,但不高于50元,日销售量y(千克)与售价x(元/千克)之间存在一次函数关系,部分图象如图所示,设该农产品的日销售利润为W元.
(1)分别求出y与x,W与x之间的函数解析式;
(2)该合作社决定从每天的销售利润中拿出200元设立“助学基金”,若捐款后合作社的剩余利润是800元,求该农产品的售价;
(3)若该农产品的日销量不低于90千克,当销售单价定为多少元时,每天获取的利润最大,最大利润是多少元.
1.某工厂计划从现在开始,在每个生产周期内生产并销售完某型号设备,该设备的生产成本为10万元件.设第个生产周期设备的售价为万元/件,售价与之间的函数解析式是,其中是正整数.当时,;当时,.
(1)求,的值:
(2)设第个生产周期生产并销售完设备的数量为件,且与满足关系式.则工厂第几个生产周期获得的利润最大?最大的利润是多少万元?
2.一次足球训练中,小华从球门正前方的A处射门,足球射向球门的运行路线呈抛物线,当球飞行的水平距离为时,球达到最高点,此时球离地面.已知球门高OB为,现以O为原点建立如图所示直角坐标系.
(1)求出抛物线的函数解析式并说明此次射门在不受干扰的情况下能否进球;
(2)若防守队员小明跳起后能摸到的最大高度为2.25米,他此时站在离球门3米远的位置,求小明至少后退多少米才能防守住这次射门?
(3)在射门路线的形状、最大高度均保持不变情况下,适当靠近球门进球的把握会更大,小华决定将足球向球门方向移动一定距离后再射门,他最多可以向球门移动__________.(填序号即可,)
①; ②; ③.
3.如图某桥拱截面可视为抛物线的一部分,在某一时刻,桥拱内的水面宽,桥拱顶点到水面的距离是.
(1)按如图所示的坐标系,求该桥拱的函数表达式;
(2)要保证高米的小船能够通过此桥(船顶与桥拱的距离不小于米),求小船的最大宽度是多少?
(3)如图,桥拱所在的函数图象的抛物线的轴下方部分与桥拱在平静水面中的倒影组成一个新函数图象.现将新函数图象向右平移()个单位长度,使得平移后的函数图象在之间,且随的增大而减小,请直接写出的取值范围.
4.高楼火灾越来越受到重视,某区消防中队开展消防技能比赛,如图,在一废弃高楼距地面的点A和其正上方点B处各设置了一个火源.消防员来到火源正前方,水枪喷出的水流看作抛物线的一部分(水流出口与地面的距离忽略不计),第一次灭火时,站在水平地面上的点C处,水流恰好到达点A处,且水流的最大高度为.待A处火熄灭后,消防员退到点D处,调整水枪进行第二次灭火,使水流恰好到达点B处,已知点D到高楼的水平距离为,假设两次灭火时水流的最高点到高楼的水平距离均为.建立如图所示的平面直角坐标系. 水流的高度与到高楼的水平距离之间的函数关系式为.
(1)求消防员第一次灭火时,水流所在抛物线的解析式;
(2)若两次灭火时,水流所在抛物线的形状相同,求A、B之间的距离;
(3)若消防员站在到高楼水平距离为的地方,想要扑灭距地面高度范围内的火苗,当水流最高点到高楼的水平距离始终为时,直接写出a的取值范围.
5.小明在一块平整场地玩弹力球,并以此情境编制一道数学题:
如图,在平面直角坐标系中,小明从点处将弹力球(看成点)扔向地面,在地面上的点B处弹起后其运动路线为抛物线,抛物线,在点C处达到最高,之后落在地面上的点D处,已知,点C坐标为.
(1)求抛物线的表达式及点D坐标;
(2)弹力球在点D处再次弹起,其运动路线为抛物线,抛物线与的形状一致且在E处最高,点E与点O的水平距离为,
①求抛物线与最高点的高度差;
②有一竖直放置的隔板高,且,若弹力球沿C下落过程中要落在隔板上(含端点),其他条件都不变的情况下,需要将起弹点B右移n米,直接写出n的取值范围.
6.一条河上横跨着一座宏伟壮观的悬索桥.桥梁的缆索与缆索均呈抛物线型,桥塔与桥塔均垂直于桥面,如图所示,以O为原点,以直线为x轴,以桥塔所在直线为y轴,建立平面直角坐标系.
已知:缆索所在抛物线与缆索所在抛物线关于y轴对称,桥塔与桥塔之间的距离,,缆索的最低点P到的距离(桥塔的粗细忽略不计)
(1)求缆索所在抛物线的函数表达式;
(2)点E在缆索上,,且,,求的长.
7.某公园在人工湖里安装一个喷泉,在湖心处竖直安装一根水管,在水管的顶端安一个喷水头,若记水柱上某一位置与水管的水平距离为米,与湖面的垂直高度为米.
(米) 0 1 2 3 4
(米)
根据上述信息,解决以下问题:
(1)在如下网格中建立适当的平面直角坐标系,并根据表中所给数据画出表示与函数关系的图象;
(2)若水柱最高点距离湖面的高度为米,则______;
(3)现公园想通过喷泉设立新的游玩项目,准备通过只调节水管露出湖面的高度,使得游船能从水柱下方通过,为避免游船被喷泉淋到,要求游船从水柱下方中间通过时,顶棚上任意一点到水柱的竖直距离均不小于米,已知游船顶棚宽度为米,顶棚到湖面的高度为米,那么公园应将水管露出湖面的高度(喷水头忽略不计)至少调节到多少米才能符合要求.(结果保留一位小数).
8.某课外科技小组制作了一架航模飞机,计划参加学校举办的航模比赛.通过试验;收集了该飞机相对于出发点飞行的水平距离(单位:)、飞行高度(单位:)随飞行时间(单位:)变化的数据,如下表所示:
飞行时间 0 2 4 6 8
飞行水平距离 0 8 16 24 32
飞行高度 0 18 32 42 48
已知与满足一次函数关系,即,与满足二次函数关系.
(1)求关于的函数解析式.(不必写出自变量的取值范围)
(2)如图,活动小组在水平安全线上的点处设置一个起飞平台试飞该航模飞机(平台的高度忽略不计).
①求飞机落到水平安全线时飞行的水平距离.
②若航模比赛规定,以该起飞平台为起点,参赛选手需要控制航模飞机在飞行水平距离为的范围内进行特技动作展示,且动作展示时飞行高度不能低于,请你判断该航模飞机此次试飞能否达到要求,并说明理由.
9.为了解新建道路的通行能力,查阅资料获知:在某种情况下,车流速度V(单位:千米/时)是车流密度x(单位:辆/千米)的函数,其函数图象如图所示.
(1)当时,求V关于x的函数表达式.
(2)车流量是单位时间内通过观测点的车辆数,计算公式为:车流量车流速度车流密度.若车流速度V不超过80千米/时,求当车流密度x为多少时,车流量P(单位:辆/时)达到最大,并求出这一最大值.
10.2024年“五一”假期期间,阆中古城景区某特产店销售A,B两类特产.A类特产进价50元/件,B类特产进价60元/件.已知购买1件A类特产和1件B类特产需132元,购买3件A类特产和5件B类特产需540元.
(1)求A类特产和B类特产每件的售价各是多少元?
(2)A类特产供货充足,按原价销售每天可售出60件.市场调查反映,若每降价1元,每天可多售出10件(每件售价不低于进价).设每件A类特产降价x元,每天的销售量为y件,求y与x的函数关系式,并写出自变量x的取值范围.
(3)在(2)的条件下,由于B类特产供货紧张,每天只能购进100件且能按原价售完.设该店每天销售这两类特产的总利润为w元,求w与x的函数关系式,并求出每件A类特产降价多少元时总利润w最大,最大利润是多少元?(利润=售价-进价)
11.人勤春来早,奋进正当时.眼下正是温室大棚育苗的好时节,大棚种植户开始了新一年的辛勤劳作,在新的一年播下希望的种子.如图是小颖爸爸在屋侧的菜地上搭建的一抛物线型蔬菜大棚,其中一端固定在离水平地面高3米的墙体A处(墙高大于4米),另一端固定在地面上的C点处,现分别以地面和墙体为x轴和y轴建立平面直角坐标系,已知大棚的高度y(米)与大棚离墙体的水平距离x(米)之间的关系式用表示,抛物线的顶点B的横坐标为2.
请根据以上信息,解答下列问题:
(1)求抛物线的函数表达式;
(2)小颖的爸爸准备在抛物线上取一点P(不与A,C重合),安装一直角形钢架对大棚进行加固(点D、E分别在y轴,x轴上,且轴,轴),小颖为爸爸设计了两种方案:
方案一:如图1,将点P设在抛物线的顶点B处,安装直角形钢架对大棚进行加固;
方案二:如图2,将点P设在到墙的水平距离为5米的抛物线上,安装直角形钢架对大棚进行加固.
方案一、二中钢架DPE所需钢材长度分别记为、,请通过计算说明哪种方案更省钢材?(忽略接口处的材料损耗)
12.芯片行业是制约我国工业发展的主要技术之一.经过大量科研、技术人员艰苦攻关,我国芯片有了新突破.某芯片实现国产化后,芯片价格大幅下降.原来每片芯片的单价为元,准备进行两次降价,如果每次降价的百分率都为,经过两次降价后的价格为(元).
(1)求与之间的函数关系式;
(2)如果该芯片经过两次降价后每片芯片单价为元,求每次降价的百分率.
13.如图,二次函数的图像交x轴于A,两点,交y轴于.
(1)求这个二次函数的解析式.
(2)点M为这个二次函数图像上一个动点,点N为坐标平面上任意一点,设点M的横坐标为m,则点N的横坐标为,且轴.
①若点N也在二次函数的图像上,求m的值;
②当线段与二次函数的图像有两个公共点时,请直接写出m的取值范围.
14.如图,某农户计划用篱笆围成一个矩形场地养殖家禽,为充分利用现有资源,该矩形场地一面靠墙(墙的长度为),另外三面用篱笆围成,中间再用篱笆把它分成三个面积相等的矩形分别养殖不同的家禽,计划购买篱笆的总长度为,设矩形场地的长为, 宽为, 面积为.
(1)分别求出y与x,s与x的函数解析式;
(2)当x为何值时,矩形场地的总面积最大?最大面积为多少?
(3)若购买的篱笆总长增加,矩形场地的最大总面积能否达到 若能,请求出x的值;若不能,请说明理由.
15.为有力有效推进乡村全面振兴,在驻村工作队的帮扶下,某村积极推动“合作社+农户”模式托起村民致富梦.村合作社推广种植某特色农产品,每千克成本为20元,规定每千克售价需超过成本,但不高于50元,日销售量y(千克)与售价x(元/千克)之间存在一次函数关系,部分图象如图所示,设该农产品的日销售利润为W元.
(1)分别求出y与x,W与x之间的函数解析式;
(2)该合作社决定从每天的销售利润中拿出200元设立“助学基金”,若捐款后合作社的剩余利润是800元,求该农产品的售价;
(3)若该农产品的日销量不低于90千克,当销售单价定为多少元时,每天获取的利润最大,最大利润是多少元.
同课章节目录
