6.3.1空间图形基本位置关系的认识 教案
文档属性
| 名称 | 6.3.1空间图形基本位置关系的认识 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 403.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-13 00:00:00 | ||
图片预览

文档简介
第六章 立体几何初步
6.3.1空间图形基本位置关系的认识
1.借助长方体,通过对图形的观察和操作,在直观中认识空间点、直线、平面的位置关系.
2.提升直观想象和数学抽象素养.
教学重点:空间点、直线、平面的位置关系.
教学难点:空间直线与平面、平面与平面的位置关系.
一、新课导入
想一想:构成平面图形的基本元素是什么?它们之间的位置关系有哪些?
追问1:构成空间立体图形的元素有哪些呢?它们之间又存在什么位置关系呢?
答案:点、线、面.
今天我们就来学习,在空间图形中点线面的位置关系是怎么样的.
设计意图:通过复习平面图形中点、线的位置关系引入空间图形中的基本位置关系,方便学生进行知识的迁移.
二、新知探究
问题1:空间图形中,点与直线、点与平面的位置关系有哪些?
追问1:点A与直线AB是什么关系?
答案:点A在直线AB上.
追问2:点A与直线BC是什么关系?
答案:点A在直线BC外(点A不在直线BC上).
总结:点与直线的位置关系:点在直线上、点在直线外.
思考:能否从集合的角度出发,用符号语言表示点与直线的位置关系呢?
答案:点可以看成是一个元素,直线可以看成是由无数个点构成的集合,所以点与直线的位置关系可以表示为:
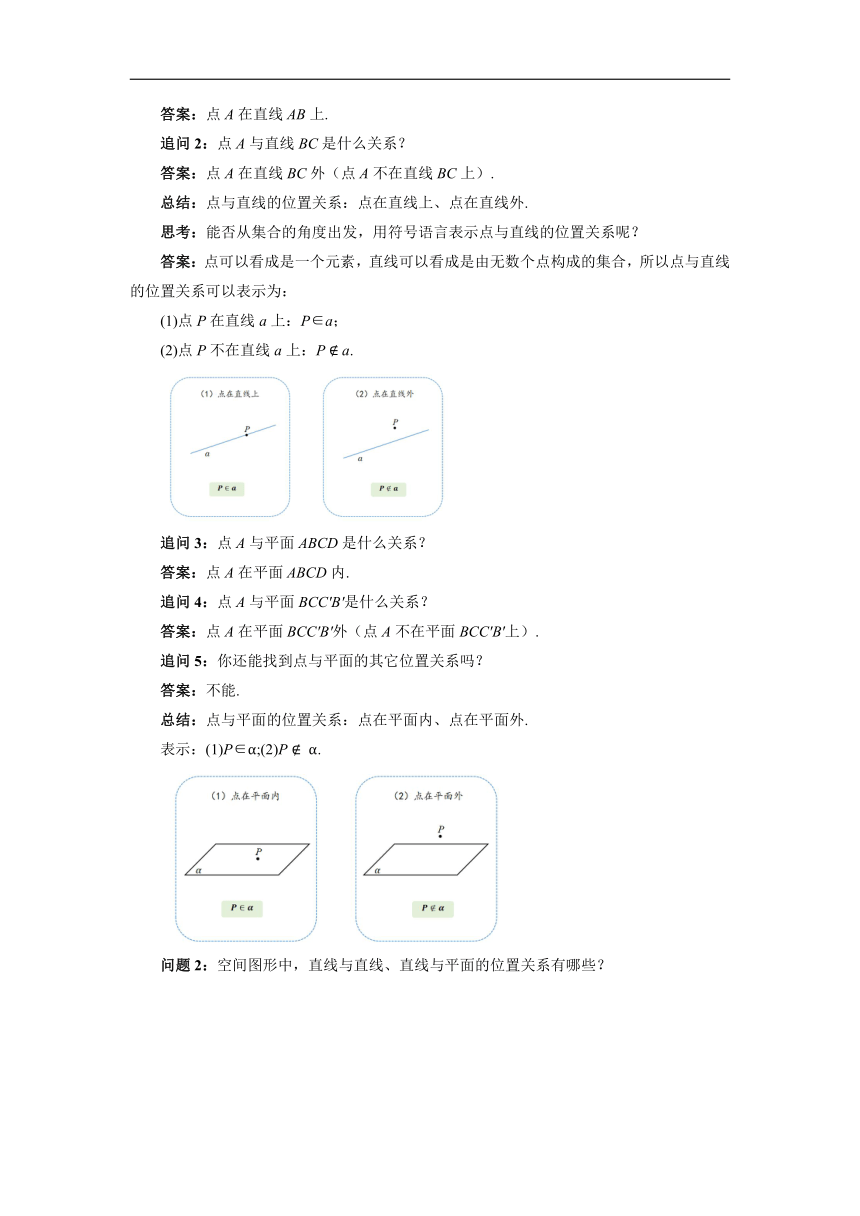
(1)点P在直线a上:P∈a;
(2)点P不在直线a上:P a.
追问3:点A与平面ABCD是什么关系?
答案:点A在平面ABCD内.
追问4:点A与平面BCC′B′是什么关系?
答案:点A在平面BCC′B′外(点A不在平面BCC′B′上).
追问5:你还能找到点与平面的其它位置关系吗?
答案:不能.
总结:点与平面的位置关系:点在平面内、点在平面外.
表示:(1)P∈;(2)P .
问题2:空间图形中,直线与直线、直线与平面的位置关系有哪些?
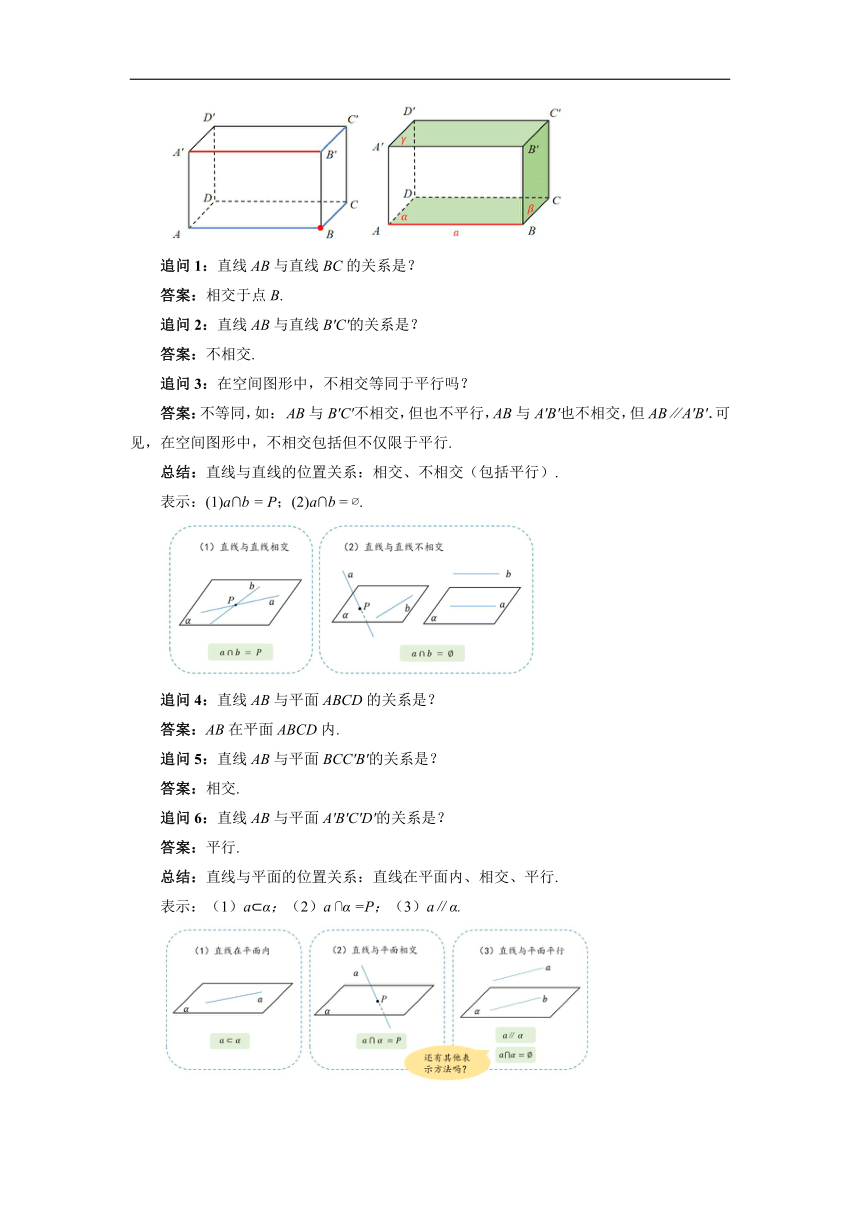
追问1:直线AB与直线BC的关系是?
答案:相交于点B.
追问2:直线AB与直线B′C′的关系是?
答案:不相交.
追问3:在空间图形中,不相交等同于平行吗?
答案:不等同,如: AB与B′C′不相交,但也不平行,AB与A′B′也不相交,但AB∥A′B′.可见,在空间图形中,不相交包括但不仅限于平行.
总结:直线与直线的位置关系:相交、不相交(包括平行).
表示:(1)a∩b = P;(2)a∩b = .
追问4:直线AB与平面ABCD的关系是?
答案:AB在平面ABCD内.
追问5:直线AB与平面BCC′B′的关系是?
答案:相交.
追问6:直线AB与平面A′B′C′D′的关系是?
答案:平行.
总结:直线与平面的位置关系:直线在平面内、相交、平行.
表示:(1)a α;(2)a α =P;(3)a∥α.
各抒己见:用符号语言表示:
(1)直线AD在哪些平面内?
(2)直线AD与哪些平面相交?
(3)直线AD与哪些平面平行?
答案:(1)AD 平面ABCD、AD 平面ADD′A′;
(2)AD 平面ABB′A′、AD 平面CDD′C′;
(3)AD∥平面BCC′B′、AD∥平面A′B′C′D′;(或AD平面BCC′B′、AD平面A′B′C′D′)
问题3:空间图形中,平面与平面的位置关系有哪些?
追问1:平面ABCD与平面BCC′B′的位置关系是?
答案:相交.
追问2:平面ABCD与平面C′B′D′A′的位置关系是?
答案:不相交(平行).
总结:平面与平面的位置关系:相交、不相交(平行).
表示:(1)α β=l;(2)α∥β.(或)
各抒己见:用符号语言表示:
(1)平面ADD′A′与哪些平面平行?
(2)平面ADD′A′与哪些平面相交?
答案:(1)平面ADD′A′∥平面BCC′B′;
平面ADD′A′平面ABB′A′、平面ADD′A′平面CDD′C′DD′、平面ADD′A′平面ABCDAD、平面ADD′A′平面A′B′C′D′A′D′.
三、应用举例
例1 画图表示下列由集合符号给出的关系:
(1)A∈α,B α,A∈l,B∈l;
(2)a α,b β,a∥c,b c=P,α β=c.
解:(1)如图所示 (2)如图所示
例2 如图所示,用符号语言可表达为( )
A. α β=m,n α,m n=A B. α β=m,n∈α,m n=A
C. α β=m,n α,A m,A n D. α β=m,n∈α,A∈m,A∈n
分析:点是元素,线、面是点的集合
n∈α错误,B、D错误
A m,A n错误,C错误
故选择A.
设计意图:通过例题,熟悉空间图形的基本位置关系.
四、课堂练习
1.在正六棱柱ABCDEF-A′B′C′D′E′F′有 条棱与棱BC平行.
2.用符号语言描述下列语句:
(1)点C在平面内;
(2)直线m与n相交与点A;
(3)点A在平面与平面的交线l上;
(4)平面内的直线a平行于平面内的直线b.
3.根据下列符号表示的语句,说明点、线、面之间的位置关系,并画出相应的图形:
(1)A∈α,B α;
(2)A∈α,m=A,A l,l α;
(3)P∈l,P α,Q∈l,Q∈α.
参考答案:
1.分析:做出正六棱柱,如图
与棱BC平行的连线有:EF、E′F′、B′C′
故共有3条.
2.(1);
(2);
(3);
(4)∥b.
3.解析:(1)点A在平面α内,点B不在平面α内;
(2)直线l在平面α内,直线m与平面α相交于点A,且点A不在直线l上;
(3)直线l经过平面α外一点P和平面α内一点Q.
图形分别如下图所示:
(1)(2)(3)
五、课堂小结
1、点与线:点在线上、点在线外
2、点与面:点在面内、点在面外
3、线与线:相交、不相交(包括平行)
4、线与面:线在面内、相交、平行
5、面与面:相交、平行
六、布置作业
教材第214页习题6-3第1题.
6.3.1空间图形基本位置关系的认识
1.借助长方体,通过对图形的观察和操作,在直观中认识空间点、直线、平面的位置关系.
2.提升直观想象和数学抽象素养.
教学重点:空间点、直线、平面的位置关系.
教学难点:空间直线与平面、平面与平面的位置关系.
一、新课导入
想一想:构成平面图形的基本元素是什么?它们之间的位置关系有哪些?
追问1:构成空间立体图形的元素有哪些呢?它们之间又存在什么位置关系呢?
答案:点、线、面.
今天我们就来学习,在空间图形中点线面的位置关系是怎么样的.
设计意图:通过复习平面图形中点、线的位置关系引入空间图形中的基本位置关系,方便学生进行知识的迁移.
二、新知探究
问题1:空间图形中,点与直线、点与平面的位置关系有哪些?
追问1:点A与直线AB是什么关系?
答案:点A在直线AB上.
追问2:点A与直线BC是什么关系?
答案:点A在直线BC外(点A不在直线BC上).
总结:点与直线的位置关系:点在直线上、点在直线外.
思考:能否从集合的角度出发,用符号语言表示点与直线的位置关系呢?
答案:点可以看成是一个元素,直线可以看成是由无数个点构成的集合,所以点与直线的位置关系可以表示为:
(1)点P在直线a上:P∈a;
(2)点P不在直线a上:P a.
追问3:点A与平面ABCD是什么关系?
答案:点A在平面ABCD内.
追问4:点A与平面BCC′B′是什么关系?
答案:点A在平面BCC′B′外(点A不在平面BCC′B′上).
追问5:你还能找到点与平面的其它位置关系吗?
答案:不能.
总结:点与平面的位置关系:点在平面内、点在平面外.
表示:(1)P∈;(2)P .
问题2:空间图形中,直线与直线、直线与平面的位置关系有哪些?
追问1:直线AB与直线BC的关系是?
答案:相交于点B.
追问2:直线AB与直线B′C′的关系是?
答案:不相交.
追问3:在空间图形中,不相交等同于平行吗?
答案:不等同,如: AB与B′C′不相交,但也不平行,AB与A′B′也不相交,但AB∥A′B′.可见,在空间图形中,不相交包括但不仅限于平行.
总结:直线与直线的位置关系:相交、不相交(包括平行).
表示:(1)a∩b = P;(2)a∩b = .
追问4:直线AB与平面ABCD的关系是?
答案:AB在平面ABCD内.
追问5:直线AB与平面BCC′B′的关系是?
答案:相交.
追问6:直线AB与平面A′B′C′D′的关系是?
答案:平行.
总结:直线与平面的位置关系:直线在平面内、相交、平行.
表示:(1)a α;(2)a α =P;(3)a∥α.
各抒己见:用符号语言表示:
(1)直线AD在哪些平面内?
(2)直线AD与哪些平面相交?
(3)直线AD与哪些平面平行?
答案:(1)AD 平面ABCD、AD 平面ADD′A′;
(2)AD 平面ABB′A′、AD 平面CDD′C′;
(3)AD∥平面BCC′B′、AD∥平面A′B′C′D′;(或AD平面BCC′B′、AD平面A′B′C′D′)
问题3:空间图形中,平面与平面的位置关系有哪些?
追问1:平面ABCD与平面BCC′B′的位置关系是?
答案:相交.
追问2:平面ABCD与平面C′B′D′A′的位置关系是?
答案:不相交(平行).
总结:平面与平面的位置关系:相交、不相交(平行).
表示:(1)α β=l;(2)α∥β.(或)
各抒己见:用符号语言表示:
(1)平面ADD′A′与哪些平面平行?
(2)平面ADD′A′与哪些平面相交?
答案:(1)平面ADD′A′∥平面BCC′B′;
平面ADD′A′平面ABB′A′、平面ADD′A′平面CDD′C′DD′、平面ADD′A′平面ABCDAD、平面ADD′A′平面A′B′C′D′A′D′.
三、应用举例
例1 画图表示下列由集合符号给出的关系:
(1)A∈α,B α,A∈l,B∈l;
(2)a α,b β,a∥c,b c=P,α β=c.
解:(1)如图所示 (2)如图所示
例2 如图所示,用符号语言可表达为( )
A. α β=m,n α,m n=A B. α β=m,n∈α,m n=A
C. α β=m,n α,A m,A n D. α β=m,n∈α,A∈m,A∈n
分析:点是元素,线、面是点的集合
n∈α错误,B、D错误
A m,A n错误,C错误
故选择A.
设计意图:通过例题,熟悉空间图形的基本位置关系.
四、课堂练习
1.在正六棱柱ABCDEF-A′B′C′D′E′F′有 条棱与棱BC平行.
2.用符号语言描述下列语句:
(1)点C在平面内;
(2)直线m与n相交与点A;
(3)点A在平面与平面的交线l上;
(4)平面内的直线a平行于平面内的直线b.
3.根据下列符号表示的语句,说明点、线、面之间的位置关系,并画出相应的图形:
(1)A∈α,B α;
(2)A∈α,m=A,A l,l α;
(3)P∈l,P α,Q∈l,Q∈α.
参考答案:
1.分析:做出正六棱柱,如图
与棱BC平行的连线有:EF、E′F′、B′C′
故共有3条.
2.(1);
(2);
(3);
(4)∥b.
3.解析:(1)点A在平面α内,点B不在平面α内;
(2)直线l在平面α内,直线m与平面α相交于点A,且点A不在直线l上;
(3)直线l经过平面α外一点P和平面α内一点Q.
图形分别如下图所示:
(1)(2)(3)
五、课堂小结
1、点与线:点在线上、点在线外
2、点与面:点在面内、点在面外
3、线与线:相交、不相交(包括平行)
4、线与面:线在面内、相交、平行
5、面与面:相交、平行
六、布置作业
教材第214页习题6-3第1题.
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
