6.6简单几何体的再认识 教案
文档属性
| 名称 | 6.6简单几何体的再认识 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 480.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-13 00:00:00 | ||
图片预览



文档简介
第六章 立体几何初步
6.6 简单几何体的再认识(1)
1.使学生能够了解柱、锥、台体的侧面积公式并运用公式求解柱、锥、台体的侧面积以及柱、锥的体积;
2.经历几何体的侧面展开过程,感知几何体的形状,培养转化与化归的能力;
3.激发学生探索创新的意识,增强学习的积极性.
教学重点:柱、锥、台体的侧面积公式的由来与计算;柱、锥体的体积公式与计算.
教学难点:展开图与空间几何体的转化.
一、新课导入
情境:有1000个这样的圆柱,现在想给它涂上一个漂亮的颜色,假如每平方米需要油漆0.1千克,那么一共需要多少千克的油漆呢?
解决这个问题的关键是什么?在于计算圆柱的表面积,而圆柱的表面积等于两个底面面积加上侧面的面积,而圆柱的侧面是曲面,如何计算圆柱的侧面(曲面)的面积呢?
今天我们就来学习曲面转化为平面的思想方法在柱、锥、台体侧面积的计算上的应用.
设计意图:通过学生们熟悉的圆柱体进行导入,给出“曲面转化为平面”的思想在此类问题中的妙用,引导学生后面对锥体、台体侧面展开上的应用.
二、新知探究
问题1:已知圆柱的底面半径为与高为,如何计算圆柱的侧面积与表面积?
分析:通过对情境中问题的思考,我们已经知道圆柱的表面积等于两个底面面积加上侧面的面积,而圆柱的侧面是曲面,能否把曲面转化为平面来计算面积呢?怎么转化呢?
追问1:把圆柱的侧面沿一条母线展开,得到的是什么图形?
答案:矩形
追问2:矩形的长和宽分别是什么?
答案:矩形的长是圆柱底面圆的周长;宽是圆柱的高
已知圆柱底面圆的半径为,高为,则圆柱的侧面积和表面积分别为:
问题2:已知圆锥的底面半径为与母线长为,如何计算圆锥的侧面积和表面积?
追问1:把圆锥的侧面沿一条母线展开,得到的是什么图形?
答案:扇形
追问2:扇形的半径和弧长分别是什么?
答案:扇形的半径是圆锥的母线,扇形的弧长是底面圆的周长
已知圆锥底面圆的半径为,母线长为,则圆锥的侧面积和表面积分别为:
问题3:已知圆台的两个底面半径分别为,,母线长为,如何求圆台的侧面积和表面积?
分析:可先将圆台还原成圆锥再展开侧面,圆台的侧面展开图是扇环,扇环面积即两扇形面积之差.
答案:由相似性可知,,所以,
小结1:圆柱、圆台、圆锥的侧面展开与侧面积
.
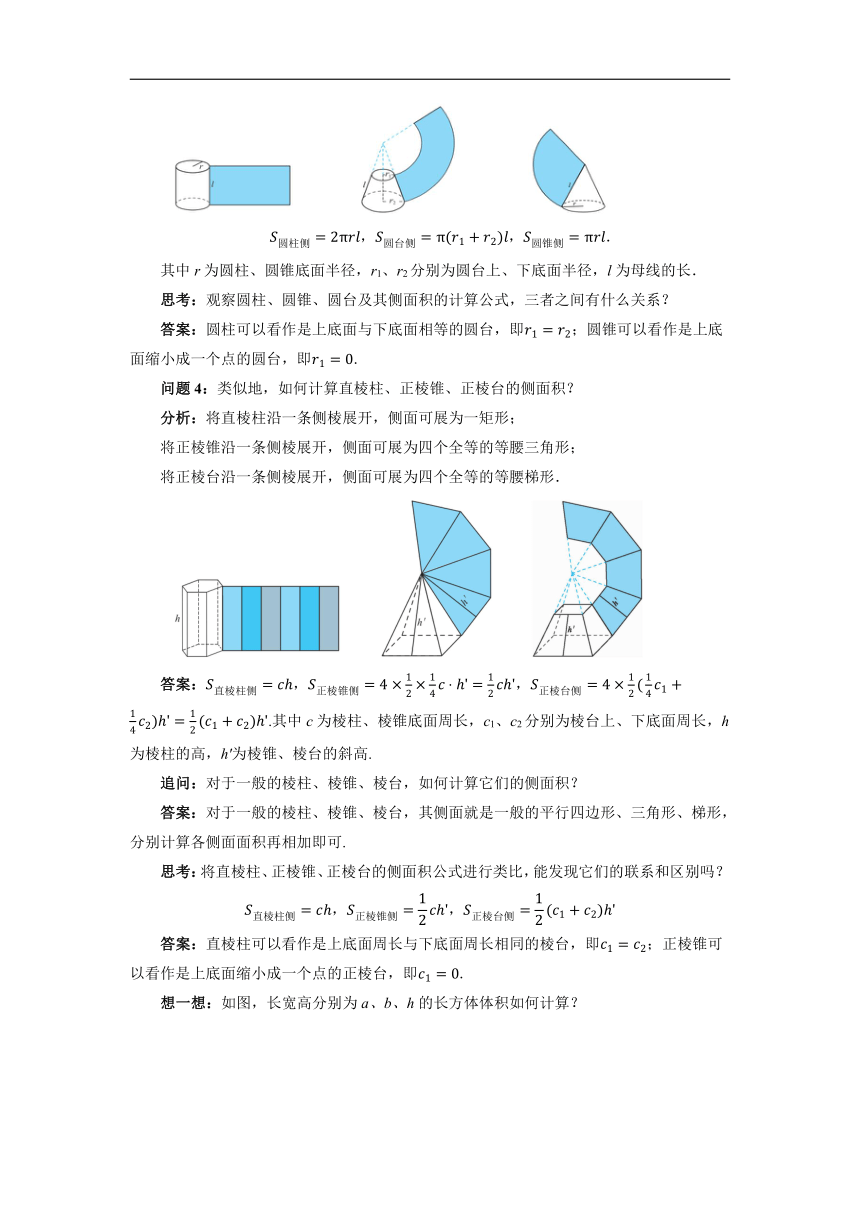
其中r为圆柱、圆锥底面半径,r1、r2分别为圆台上、下底面半径,l为母线的长.
思考:观察圆柱、圆锥、圆台及其侧面积的计算公式,三者之间有什么关系?
答案:圆柱可以看作是上底面与下底面相等的圆台,即;圆锥可以看作是上底面缩小成一个点的圆台,即.
问题4:类似地,如何计算直棱柱、正棱锥、正棱台的侧面积?
分析:将直棱柱沿一条侧棱展开,侧面可展为一矩形;
将正棱锥沿一条侧棱展开,侧面可展为四个全等的等腰三角形;
将正棱台沿一条侧棱展开,侧面可展为四个全等的等腰梯形.
答案:.其中c为棱柱、棱锥底面周长,c1、c2分别为棱台上、下底面周长,h为棱柱的高,h′为棱锥、棱台的斜高.
追问:对于一般的棱柱、棱锥、棱台,如何计算它们的侧面积?
答案:对于一般的棱柱、棱锥、棱台,其侧面就是一般的平行四边形、三角形、梯形,分别计算各侧面面积再相加即可.
思考:将直棱柱、正棱锥、正棱台的侧面积公式进行类比,能发现它们的联系和区别吗?
答案:直棱柱可以看作是上底面周长与下底面周长相同的棱台,即;正棱锥可以看作是上底面缩小成一个点的正棱台,即.
想一想:如图,长宽高分别为a、b、h的长方体体积如何计算?
答案:.我们知道,长方体实际上就是直四棱柱,所以我们可知.
猜想:对于一般的棱柱,体积该如何计算?
答案:.其中,S为柱体的底面积,h为柱体的高.由祖暅原理知,该公式对圆柱同样适用.
问题5:如图,三棱柱ABC-A′B′C′中,连接A′C、A′B、B′C,得到三个三棱锥A′-ABC、C-A′B′C′、A′-BCB′,比较其体积V1、V2、V3的大小.
答案:不妨设三棱柱的高为h,点A′到BCC′B′的距离为h′,
由图可知,三棱锥A′-ABC、C-A′B′C′等底同高(高为h),故;
三棱锥C-A′B′C′、A′-BCB′等底同高(高为h′),故;
故.
追问:由此你能得出什么结论?
答案:棱柱的体积是与它同底等高的棱锥体积的3倍,.同样地,该公式对圆锥也适用.
小结3:柱体、锥体的体积
,,其中,S为柱体、锥体的底面积,h为柱体、锥体的高.
三、应用举例
例1 一个圆柱形的锅炉,底面直径d=1 m,高h=2.3 m,求锅炉的表面积(精确到 0.1 m2).
分析:注意直径是半径的两倍,计算表面积要在侧面积的基础上加底面积的两倍.
解:
因此,锅炉的表面积约为.
例2 圆台的上、下底面半径分别是10 cm 和20 cm ,它的侧面展开图的扇环的圆心角是180°,那么圆台的侧面积是多少?(结果中保留)
分析:利用扇环圆心角,可求SA、SB长,作差可得母线长,进而可求侧面积.
解:如图,设圆台上底面周长为c cm,
∵圆环的圆心角是180°,∴.
又∵ (cm),
∴SA=20 cm.同理SB=40 cm.
∴AB=SB SA=20 (cm),
(cm2)
因此,圆台的侧面积为600 cm2.
例3 一个正三棱台的上、下底面边长分别为 3 cm 和 6 cm ,高是 cm.求这个正三棱台的侧面积.
解:如图,点O1,O分别是上、下底面的中心,则 cm.
连接并延长交于点,连接并延长交BC于点D;
过作AD的垂线,垂足为点E;连接.
在Rt△D1ED中, cm,
(cm),
(cm).
∴(cm2),
∴三棱台的侧面积为 cm2.
例4 埃及胡夫金字塔大约建于公元前 2580 年,其形状为正四棱锥.塔高约 146.6 m,底面边长约 230.4 m.求这座金字塔的侧面积和体积.(精确到 0.1)
解:如图,AC为高,BC为底面的边心距,则AC=146.6 m,BC=115.2 m,
底面周长c=4×230.4 m.
(m2)
(m3)
因此,金字塔的侧面积约为85 914.9 m2,体积约为2 594 046.0 m3.
设计意图:通过例题,帮助学生巩固柱体、锥体、台体的侧面展开及侧面积、体积的计算.
四、课堂练习
1.轴截面是边长为2的正三角形的圆锥的侧面积是 .
2.陀螺是中国民间的娱乐工具之一,其形状结构如图所示,由一个同底的圆柱体和圆锥体组合而成,若圆锥体和圆柱体的高以及底面圆的半径长分别为h1、h2、r,且h1=h2=2r,设圆锥体的侧面积和圆柱体的侧面积分别为S1和S2,则 = .
3. 如图所示,一竖立在地面上的圆锥形物体的母线长为2,一只小虫从圆锥的底面圆上的点P出发,绕圆锥爬行一周后回到点P处,若该小虫爬行的最短路程为,求这个圆锥的表面积.
4.如图,圆锥底面半径为1,高为3.求圆锥内接圆柱(一底面在圆锥底面上,另一底面切于圆锥侧面)侧面积的最大值.
参考答案:
1.∵圆锥的轴截面是边长为2的正三角形,
∴底面半径r=1,母线长l=2,
∴.
故答案为.
2.由题意,圆锥的母线,
则,,
∴.
故答案为.
3.如图,PP′是小虫爬行的最短路程.
由余弦定理可得,
∴,设底面圆的半径为r,
则有,解得.
∴.
4.设圆柱的底面半径为r,高为h,
由相似性可得:,解得,
∴,
当时,内接圆柱侧面积取得最大值.
五、课堂小结
一、圆柱、圆锥、圆台的侧面展开与侧面积
其中r为圆柱、圆锥底面半径,r1、r2分别为圆台上、下底面半径,l为母线的长.
二、直棱柱、正棱锥、正棱台的侧面展开与侧面积
其中c为棱柱、棱锥底面周长,c1、c2分别为棱台上、下底面周长,h为棱柱的高,h′为棱锥、棱台的斜高.
三、柱体、锥体的体积
,,其中,S为柱体、锥体的底面积,h为柱体、锥体的高.
设计意图:引导学生对本节课所学知识方法有一个全面的认识,培养学生的归纳总结能力,帮助学生深化对知识的理解与掌握,体会研究解决实际问题的思路、途径、方法,为进一步学习打下坚实基础.
六、布置作业
教材第241页练习第1、2、3题.
6.6 简单几何体的再认识(1)
1.使学生能够了解柱、锥、台体的侧面积公式并运用公式求解柱、锥、台体的侧面积以及柱、锥的体积;
2.经历几何体的侧面展开过程,感知几何体的形状,培养转化与化归的能力;
3.激发学生探索创新的意识,增强学习的积极性.
教学重点:柱、锥、台体的侧面积公式的由来与计算;柱、锥体的体积公式与计算.
教学难点:展开图与空间几何体的转化.
一、新课导入
情境:有1000个这样的圆柱,现在想给它涂上一个漂亮的颜色,假如每平方米需要油漆0.1千克,那么一共需要多少千克的油漆呢?
解决这个问题的关键是什么?在于计算圆柱的表面积,而圆柱的表面积等于两个底面面积加上侧面的面积,而圆柱的侧面是曲面,如何计算圆柱的侧面(曲面)的面积呢?
今天我们就来学习曲面转化为平面的思想方法在柱、锥、台体侧面积的计算上的应用.
设计意图:通过学生们熟悉的圆柱体进行导入,给出“曲面转化为平面”的思想在此类问题中的妙用,引导学生后面对锥体、台体侧面展开上的应用.
二、新知探究
问题1:已知圆柱的底面半径为与高为,如何计算圆柱的侧面积与表面积?
分析:通过对情境中问题的思考,我们已经知道圆柱的表面积等于两个底面面积加上侧面的面积,而圆柱的侧面是曲面,能否把曲面转化为平面来计算面积呢?怎么转化呢?
追问1:把圆柱的侧面沿一条母线展开,得到的是什么图形?
答案:矩形
追问2:矩形的长和宽分别是什么?
答案:矩形的长是圆柱底面圆的周长;宽是圆柱的高
已知圆柱底面圆的半径为,高为,则圆柱的侧面积和表面积分别为:
问题2:已知圆锥的底面半径为与母线长为,如何计算圆锥的侧面积和表面积?
追问1:把圆锥的侧面沿一条母线展开,得到的是什么图形?
答案:扇形
追问2:扇形的半径和弧长分别是什么?
答案:扇形的半径是圆锥的母线,扇形的弧长是底面圆的周长
已知圆锥底面圆的半径为,母线长为,则圆锥的侧面积和表面积分别为:
问题3:已知圆台的两个底面半径分别为,,母线长为,如何求圆台的侧面积和表面积?
分析:可先将圆台还原成圆锥再展开侧面,圆台的侧面展开图是扇环,扇环面积即两扇形面积之差.
答案:由相似性可知,,所以,
小结1:圆柱、圆台、圆锥的侧面展开与侧面积
.
其中r为圆柱、圆锥底面半径,r1、r2分别为圆台上、下底面半径,l为母线的长.
思考:观察圆柱、圆锥、圆台及其侧面积的计算公式,三者之间有什么关系?
答案:圆柱可以看作是上底面与下底面相等的圆台,即;圆锥可以看作是上底面缩小成一个点的圆台,即.
问题4:类似地,如何计算直棱柱、正棱锥、正棱台的侧面积?
分析:将直棱柱沿一条侧棱展开,侧面可展为一矩形;
将正棱锥沿一条侧棱展开,侧面可展为四个全等的等腰三角形;
将正棱台沿一条侧棱展开,侧面可展为四个全等的等腰梯形.
答案:.其中c为棱柱、棱锥底面周长,c1、c2分别为棱台上、下底面周长,h为棱柱的高,h′为棱锥、棱台的斜高.
追问:对于一般的棱柱、棱锥、棱台,如何计算它们的侧面积?
答案:对于一般的棱柱、棱锥、棱台,其侧面就是一般的平行四边形、三角形、梯形,分别计算各侧面面积再相加即可.
思考:将直棱柱、正棱锥、正棱台的侧面积公式进行类比,能发现它们的联系和区别吗?
答案:直棱柱可以看作是上底面周长与下底面周长相同的棱台,即;正棱锥可以看作是上底面缩小成一个点的正棱台,即.
想一想:如图,长宽高分别为a、b、h的长方体体积如何计算?
答案:.我们知道,长方体实际上就是直四棱柱,所以我们可知.
猜想:对于一般的棱柱,体积该如何计算?
答案:.其中,S为柱体的底面积,h为柱体的高.由祖暅原理知,该公式对圆柱同样适用.
问题5:如图,三棱柱ABC-A′B′C′中,连接A′C、A′B、B′C,得到三个三棱锥A′-ABC、C-A′B′C′、A′-BCB′,比较其体积V1、V2、V3的大小.
答案:不妨设三棱柱的高为h,点A′到BCC′B′的距离为h′,
由图可知,三棱锥A′-ABC、C-A′B′C′等底同高(高为h),故;
三棱锥C-A′B′C′、A′-BCB′等底同高(高为h′),故;
故.
追问:由此你能得出什么结论?
答案:棱柱的体积是与它同底等高的棱锥体积的3倍,.同样地,该公式对圆锥也适用.
小结3:柱体、锥体的体积
,,其中,S为柱体、锥体的底面积,h为柱体、锥体的高.
三、应用举例
例1 一个圆柱形的锅炉,底面直径d=1 m,高h=2.3 m,求锅炉的表面积(精确到 0.1 m2).
分析:注意直径是半径的两倍,计算表面积要在侧面积的基础上加底面积的两倍.
解:
因此,锅炉的表面积约为.
例2 圆台的上、下底面半径分别是10 cm 和20 cm ,它的侧面展开图的扇环的圆心角是180°,那么圆台的侧面积是多少?(结果中保留)
分析:利用扇环圆心角,可求SA、SB长,作差可得母线长,进而可求侧面积.
解:如图,设圆台上底面周长为c cm,
∵圆环的圆心角是180°,∴.
又∵ (cm),
∴SA=20 cm.同理SB=40 cm.
∴AB=SB SA=20 (cm),
(cm2)
因此,圆台的侧面积为600 cm2.
例3 一个正三棱台的上、下底面边长分别为 3 cm 和 6 cm ,高是 cm.求这个正三棱台的侧面积.
解:如图,点O1,O分别是上、下底面的中心,则 cm.
连接并延长交于点,连接并延长交BC于点D;
过作AD的垂线,垂足为点E;连接.
在Rt△D1ED中, cm,
(cm),
(cm).
∴(cm2),
∴三棱台的侧面积为 cm2.
例4 埃及胡夫金字塔大约建于公元前 2580 年,其形状为正四棱锥.塔高约 146.6 m,底面边长约 230.4 m.求这座金字塔的侧面积和体积.(精确到 0.1)
解:如图,AC为高,BC为底面的边心距,则AC=146.6 m,BC=115.2 m,
底面周长c=4×230.4 m.
(m2)
(m3)
因此,金字塔的侧面积约为85 914.9 m2,体积约为2 594 046.0 m3.
设计意图:通过例题,帮助学生巩固柱体、锥体、台体的侧面展开及侧面积、体积的计算.
四、课堂练习
1.轴截面是边长为2的正三角形的圆锥的侧面积是 .
2.陀螺是中国民间的娱乐工具之一,其形状结构如图所示,由一个同底的圆柱体和圆锥体组合而成,若圆锥体和圆柱体的高以及底面圆的半径长分别为h1、h2、r,且h1=h2=2r,设圆锥体的侧面积和圆柱体的侧面积分别为S1和S2,则 = .
3. 如图所示,一竖立在地面上的圆锥形物体的母线长为2,一只小虫从圆锥的底面圆上的点P出发,绕圆锥爬行一周后回到点P处,若该小虫爬行的最短路程为,求这个圆锥的表面积.
4.如图,圆锥底面半径为1,高为3.求圆锥内接圆柱(一底面在圆锥底面上,另一底面切于圆锥侧面)侧面积的最大值.
参考答案:
1.∵圆锥的轴截面是边长为2的正三角形,
∴底面半径r=1,母线长l=2,
∴.
故答案为.
2.由题意,圆锥的母线,
则,,
∴.
故答案为.
3.如图,PP′是小虫爬行的最短路程.
由余弦定理可得,
∴,设底面圆的半径为r,
则有,解得.
∴.
4.设圆柱的底面半径为r,高为h,
由相似性可得:,解得,
∴,
当时,内接圆柱侧面积取得最大值.
五、课堂小结
一、圆柱、圆锥、圆台的侧面展开与侧面积
其中r为圆柱、圆锥底面半径,r1、r2分别为圆台上、下底面半径,l为母线的长.
二、直棱柱、正棱锥、正棱台的侧面展开与侧面积
其中c为棱柱、棱锥底面周长,c1、c2分别为棱台上、下底面周长,h为棱柱的高,h′为棱锥、棱台的斜高.
三、柱体、锥体的体积
,,其中,S为柱体、锥体的底面积,h为柱体、锥体的高.
设计意图:引导学生对本节课所学知识方法有一个全面的认识,培养学生的归纳总结能力,帮助学生深化对知识的理解与掌握,体会研究解决实际问题的思路、途径、方法,为进一步学习打下坚实基础.
六、布置作业
教材第241页练习第1、2、3题.
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
