2.1 复数的加法与减法 教案
文档属性
| 名称 | 2.1 复数的加法与减法 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 360.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-13 17:20:57 | ||
图片预览


文档简介
第五章 复数
§2 2.1复数的加法与减法
1.掌握复数代数形式的加减运算法则.
2.了解复数代数形式的加减运算的几何意义.
3.借助复数代数形式的加减运算与几何意义提升数学运算、直观想象的素养.
教学重点:复数的加、减运算.
教学难点:复数加减的几何意义.
PPT课件.
一、探索新知
问题1前面我们学习了复数的概念、复数的几何意义.请问复数i与复平面内的点、向量是什么关系?
师生活动:学生回忆,举手回答.
预设答案:一一对应关系.
问题2我们知道实数、向量的加减都有相应的运算法则,那么如何进行复数的加减运算呢?
师生活动:学生思考,教师提示.
预设答案:我们这节课要研究的就是复数的加减运算,下面我们一起探究复数的运算.
设计意图:通过复习引入本节的内容---§2 2.1复数的加法与减法.(板书)
1.复数的加法与减法
问题3:类比多选式的加法运算,想一想复数如何进行加法的运算?
师生活动:学生独立思考,举手回答.
预设答案:两个复数相加就是把实部与实部、虚部与虚部分别相加.
追问:设z1=a+bi,z2=c+di是任意两个复数,如何求z1+z2的值?
师生活动:学生独立思考,举手回答.
预设答案:z1+z2=(a+bi)+(c+di)=(a+c)+(b+d)i.
设计意图:推导复数加法的运算.
问题4:若z1=a+bi,z2=c+di,如何求z1-z2?
师生活动:学生思考,小组讨论.
预设答案:z1-z2=(a+bi)-(c+di)=(a-c)+(b-d)i.
设计意图:探究复数的减法运算.
问题5:你能写出复数的加法的交换律和结合律吗?你能证明复数加法的结合律吗?
师生活动:学生阅读教材第170页,证明加法的结合和交换律,小组讨论.
预设答案:对任意z1,z2,z3∈C,有①z1+z2=z2+z1;②(z1+z2)+z3=z1+(z2+z3).
能,证明:设z1=a+bi,z2=c+di(a,b,c,d∈R),z3=x+yi,(x,y∈R),
则(z1+z2)+z3=,
z1+(z2+z3) =,
所以(z1+z2)+z3=z1+(z2+z3)。
设计意图:探究复数加法的运算律.
问题6两个复数的和是什么数,它的值唯一确定吗?
师生活动:学生独立思考,举手回答.
预设答案:是复数,唯一确定.
设计意图:帮助学生理解复数的加法运算.
问题7:如何计算(5+3i)+(24i)+(4i)?
师生活动:学生思考、计算.
预设答案:5i.
设计意图:巩固向量加法的运算.
2.复数加法的几何意义
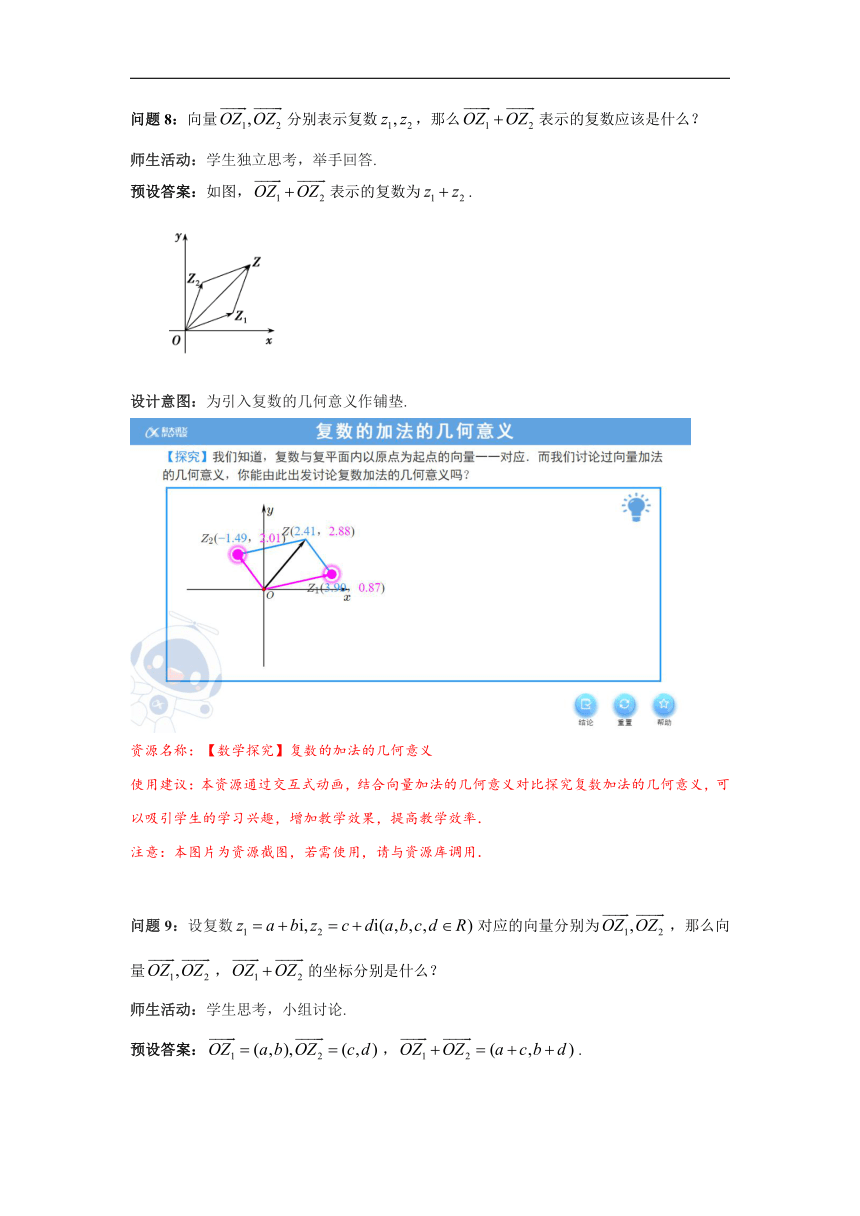
问题8:向量分别表示复数,那么表示的复数应该是什么?
师生活动:学生独立思考,举手回答.
预设答案:如图,表示的复数为.
设计意图:为引入复数的几何意义作铺垫.
资源名称:【数学探究】复数的加法的几何意义
使用建议:本资源通过交互式动画,结合向量加法的几何意义对比探究复数加法的几何意义,可以吸引学生的学习兴趣,增加教学效果,提高教学效率.
注意:本图片为资源截图,若需使用,请与资源库调用.
问题9:设复数对应的向量分别为,那么向量,的坐标分别是什么?
师生活动:学生思考,小组讨论.
预设答案:,.
问题10:根据上述分析,总结复数加法的几何意义?
师生活动:学生思考、归纳.
预设答案:如图所示,分别与向量,
对应,则.
这说明两个向量的和就与复数(a+c)+(b+d)i是对应的向量.因此复数的加法可以按照向量的加法来进行,这就是复数加法的几何意义.
问题11:类比绝对值|x-x0|的几何意义,|z-z0|(z,z0∈C)的几何意义是什么?
师生活动:教师引导学生思考,并补充完善.
预设答案:|z-z0|(z,z0∈C)的几何意义是复平面内点Z到点Z0的距离.
设计意图:巩固复数加法的几何意义.
二、初步应用
例1设,求与.
师生活动:学生分析解题思路,写出解题过程.
预设答案:,.(详解参考教材P169例2的解析.)
设计意图:巩固复数的相关概念.
例2 已知向量对应的复数是,请计算的结果,并给出几何解释.
师生活动:学生分析解题思路,板书解题过程.
预设答案:。(详解参考教材P170例4的解析.)
设计意图:巩固复数加法的几何意义.
例3已知|z1|=|z2|=|z1-z2|=1,求|z1+z2|.
师生活动:学生分析解题思路,教师板书解题过程.
预设答案:解法一:设z1=a+bi,z2=c+di(a,b,c,d∈R),
∵|z1|=|z2|=|z1-z2|=1,
∴a2+b2=c2+d2=1,①
(a-c)2+(b-d)2=1.②
由①②得2ac+2bd=1.
∴|z1+z2|=
=.
解法二:设O为坐标原点,z1,z2,z1+z2对应的点分别为A,B,C.
∵|z1|=|z2|=|z1-z2|=1,∴OAB是边长为1的正三角形,
∴四边形OACB是一个内角为60°,边长为1的菱形,且|z1+z2|是菱形的较长的对角线OC的长,∴|z1+z2|=|OC|
=.
设计意图:巩固复数加法的几何意义的应用.
练习:教科书第171页练习1,2.
师生活动:学生做练习,教师根据学生练习情况给予点评指导.
【板书设计】
§2 2.1复数的加法与减法
一、探索新知 二、初步应用
1.复数的加法与减法 例1
例2
2.复数加法的几何意义 例3
【课堂小结】
三、归纳小结,布置作业
问题12:通过本节课的学习,你有什么收获?可以从以下几个问题归纳.
(1)复数代数形式的加、减法运算方法是什么?
(2)用复数加、减运算的几何意义的解题技巧是什么?
(3)满足|z|=1的所有复数z对应的点组成什么图形?
(4)若|z-1|=|z+1|,则复数z对应的点组成什么图形?
师生活动:学生尝试总结,老师适当补充.
预设的答案:
(1)复数与复数相加减,相当于多项式加减法的合并同类项,将两个复数的实部与实部相加(减),虚部与虚部相加(减).
(2)形转化为数:利用几何意义可以把几何图形的变换转化成复数运算去处理.
数转化为形:对于一些复数运算也可以给予几何解释,使复数作为工具运用于几何之中.
(3)满足|z|=1的所有复数z对应的点在以原点为圆心,半径为1的圆上.
(4)∵|z-1|=|z+1|,∴点Z到(1,0)和(-1,0)的距离相等,即点Z在以(1,0)和(-1,0)为端点的线段的中垂线上.
布置作业:教科书第167页,A组1.
四、目标检测设计
1.复数z1=3+i,z2=1-i,则z1-z2在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
设计意图:检查学生对复数加减法的掌握情况.
2.□ABCD中,点A、B、C分别对应复数4+i、3+4i、3-5i,则点D对应的复数是( )
A.2-3i B.4+8i C.4-8i D.1+4i
设计意图:检查学生对加法运算与几何意义的掌握情况.
3.已知复数z1=a2-3-i,z2=-2a+a2i,若z1+z2是纯虚数,则实数a= .
设计意图:检查学生对复数加法的掌握情况.
4.已知平行四边形ABCD中,与对应的复数分别是3+2i与1+4i,两对角线AC与BD相交于P点.
(1)求对应的复数;
(2)求对应的复数;
(3)求APB的面积.
设计意图:检查学生对加法运算与几何意义的掌握情况.
参考答案:
1.A ∵z1-z2=(3+i)-(1-i)=2+2i,∴z1-z2在复平面内对应的点位于第一象限.
2.C 对应的复数为(3+4i)-(4+i)=(3-4)+(4-1)i=-1+3i,
设点D对应的复数为z,则对应的复数为(3-5i)-z.
由平行四边形法则知=,
∴-1+3i=(3-5i)-z,
∴z=(3-5i)-(-1+3i)=(3+1)+(-5-3)i=4-8i.故应选C.
3.3由条件知z1+z2=a2-2a-3+(a2-1)i,又z1+z2是纯虚数,所以,解得a=3.
4.解析:(1)由于ABCD是平行四边形,所以,于是,而(1+4i)-(3+2i)=-2+2i,即对应的复数是-2+2i.
(2)由于,而(3+2i)-(-2+2i)=5,即对应的复数是5.
(3)由于,,
于是,而||=,||=,
所以·cos∠APB=,
因此cos∠APB=-,故sin∠APB=,
故S△APB=sin∠APB=,即APB的面积为.
教学目标
教学重难点
课前准备
教学过程
§2 2.1复数的加法与减法
1.掌握复数代数形式的加减运算法则.
2.了解复数代数形式的加减运算的几何意义.
3.借助复数代数形式的加减运算与几何意义提升数学运算、直观想象的素养.
教学重点:复数的加、减运算.
教学难点:复数加减的几何意义.
PPT课件.
一、探索新知
问题1前面我们学习了复数的概念、复数的几何意义.请问复数i与复平面内的点、向量是什么关系?
师生活动:学生回忆,举手回答.
预设答案:一一对应关系.
问题2我们知道实数、向量的加减都有相应的运算法则,那么如何进行复数的加减运算呢?
师生活动:学生思考,教师提示.
预设答案:我们这节课要研究的就是复数的加减运算,下面我们一起探究复数的运算.
设计意图:通过复习引入本节的内容---§2 2.1复数的加法与减法.(板书)
1.复数的加法与减法
问题3:类比多选式的加法运算,想一想复数如何进行加法的运算?
师生活动:学生独立思考,举手回答.
预设答案:两个复数相加就是把实部与实部、虚部与虚部分别相加.
追问:设z1=a+bi,z2=c+di是任意两个复数,如何求z1+z2的值?
师生活动:学生独立思考,举手回答.
预设答案:z1+z2=(a+bi)+(c+di)=(a+c)+(b+d)i.
设计意图:推导复数加法的运算.
问题4:若z1=a+bi,z2=c+di,如何求z1-z2?
师生活动:学生思考,小组讨论.
预设答案:z1-z2=(a+bi)-(c+di)=(a-c)+(b-d)i.
设计意图:探究复数的减法运算.
问题5:你能写出复数的加法的交换律和结合律吗?你能证明复数加法的结合律吗?
师生活动:学生阅读教材第170页,证明加法的结合和交换律,小组讨论.
预设答案:对任意z1,z2,z3∈C,有①z1+z2=z2+z1;②(z1+z2)+z3=z1+(z2+z3).
能,证明:设z1=a+bi,z2=c+di(a,b,c,d∈R),z3=x+yi,(x,y∈R),
则(z1+z2)+z3=,
z1+(z2+z3) =,
所以(z1+z2)+z3=z1+(z2+z3)。
设计意图:探究复数加法的运算律.
问题6两个复数的和是什么数,它的值唯一确定吗?
师生活动:学生独立思考,举手回答.
预设答案:是复数,唯一确定.
设计意图:帮助学生理解复数的加法运算.
问题7:如何计算(5+3i)+(24i)+(4i)?
师生活动:学生思考、计算.
预设答案:5i.
设计意图:巩固向量加法的运算.
2.复数加法的几何意义
问题8:向量分别表示复数,那么表示的复数应该是什么?
师生活动:学生独立思考,举手回答.
预设答案:如图,表示的复数为.
设计意图:为引入复数的几何意义作铺垫.
资源名称:【数学探究】复数的加法的几何意义
使用建议:本资源通过交互式动画,结合向量加法的几何意义对比探究复数加法的几何意义,可以吸引学生的学习兴趣,增加教学效果,提高教学效率.
注意:本图片为资源截图,若需使用,请与资源库调用.
问题9:设复数对应的向量分别为,那么向量,的坐标分别是什么?
师生活动:学生思考,小组讨论.
预设答案:,.
问题10:根据上述分析,总结复数加法的几何意义?
师生活动:学生思考、归纳.
预设答案:如图所示,分别与向量,
对应,则.
这说明两个向量的和就与复数(a+c)+(b+d)i是对应的向量.因此复数的加法可以按照向量的加法来进行,这就是复数加法的几何意义.
问题11:类比绝对值|x-x0|的几何意义,|z-z0|(z,z0∈C)的几何意义是什么?
师生活动:教师引导学生思考,并补充完善.
预设答案:|z-z0|(z,z0∈C)的几何意义是复平面内点Z到点Z0的距离.
设计意图:巩固复数加法的几何意义.
二、初步应用
例1设,求与.
师生活动:学生分析解题思路,写出解题过程.
预设答案:,.(详解参考教材P169例2的解析.)
设计意图:巩固复数的相关概念.
例2 已知向量对应的复数是,请计算的结果,并给出几何解释.
师生活动:学生分析解题思路,板书解题过程.
预设答案:。(详解参考教材P170例4的解析.)
设计意图:巩固复数加法的几何意义.
例3已知|z1|=|z2|=|z1-z2|=1,求|z1+z2|.
师生活动:学生分析解题思路,教师板书解题过程.
预设答案:解法一:设z1=a+bi,z2=c+di(a,b,c,d∈R),
∵|z1|=|z2|=|z1-z2|=1,
∴a2+b2=c2+d2=1,①
(a-c)2+(b-d)2=1.②
由①②得2ac+2bd=1.
∴|z1+z2|=
=.
解法二:设O为坐标原点,z1,z2,z1+z2对应的点分别为A,B,C.
∵|z1|=|z2|=|z1-z2|=1,∴OAB是边长为1的正三角形,
∴四边形OACB是一个内角为60°,边长为1的菱形,且|z1+z2|是菱形的较长的对角线OC的长,∴|z1+z2|=|OC|
=.
设计意图:巩固复数加法的几何意义的应用.
练习:教科书第171页练习1,2.
师生活动:学生做练习,教师根据学生练习情况给予点评指导.
【板书设计】
§2 2.1复数的加法与减法
一、探索新知 二、初步应用
1.复数的加法与减法 例1
例2
2.复数加法的几何意义 例3
【课堂小结】
三、归纳小结,布置作业
问题12:通过本节课的学习,你有什么收获?可以从以下几个问题归纳.
(1)复数代数形式的加、减法运算方法是什么?
(2)用复数加、减运算的几何意义的解题技巧是什么?
(3)满足|z|=1的所有复数z对应的点组成什么图形?
(4)若|z-1|=|z+1|,则复数z对应的点组成什么图形?
师生活动:学生尝试总结,老师适当补充.
预设的答案:
(1)复数与复数相加减,相当于多项式加减法的合并同类项,将两个复数的实部与实部相加(减),虚部与虚部相加(减).
(2)形转化为数:利用几何意义可以把几何图形的变换转化成复数运算去处理.
数转化为形:对于一些复数运算也可以给予几何解释,使复数作为工具运用于几何之中.
(3)满足|z|=1的所有复数z对应的点在以原点为圆心,半径为1的圆上.
(4)∵|z-1|=|z+1|,∴点Z到(1,0)和(-1,0)的距离相等,即点Z在以(1,0)和(-1,0)为端点的线段的中垂线上.
布置作业:教科书第167页,A组1.
四、目标检测设计
1.复数z1=3+i,z2=1-i,则z1-z2在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
设计意图:检查学生对复数加减法的掌握情况.
2.□ABCD中,点A、B、C分别对应复数4+i、3+4i、3-5i,则点D对应的复数是( )
A.2-3i B.4+8i C.4-8i D.1+4i
设计意图:检查学生对加法运算与几何意义的掌握情况.
3.已知复数z1=a2-3-i,z2=-2a+a2i,若z1+z2是纯虚数,则实数a= .
设计意图:检查学生对复数加法的掌握情况.
4.已知平行四边形ABCD中,与对应的复数分别是3+2i与1+4i,两对角线AC与BD相交于P点.
(1)求对应的复数;
(2)求对应的复数;
(3)求APB的面积.
设计意图:检查学生对加法运算与几何意义的掌握情况.
参考答案:
1.A ∵z1-z2=(3+i)-(1-i)=2+2i,∴z1-z2在复平面内对应的点位于第一象限.
2.C 对应的复数为(3+4i)-(4+i)=(3-4)+(4-1)i=-1+3i,
设点D对应的复数为z,则对应的复数为(3-5i)-z.
由平行四边形法则知=,
∴-1+3i=(3-5i)-z,
∴z=(3-5i)-(-1+3i)=(3+1)+(-5-3)i=4-8i.故应选C.
3.3由条件知z1+z2=a2-2a-3+(a2-1)i,又z1+z2是纯虚数,所以,解得a=3.
4.解析:(1)由于ABCD是平行四边形,所以,于是,而(1+4i)-(3+2i)=-2+2i,即对应的复数是-2+2i.
(2)由于,而(3+2i)-(-2+2i)=5,即对应的复数是5.
(3)由于,,
于是,而||=,||=,
所以·cos∠APB=,
因此cos∠APB=-,故sin∠APB=,
故S△APB=sin∠APB=,即APB的面积为.
教学目标
教学重难点
课前准备
教学过程
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
