【湘教版数学九年级上册同步练习】 第二章一元二次方程综合检测题(含答案)
文档属性
| 名称 | 【湘教版数学九年级上册同步练习】 第二章一元二次方程综合检测题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 6.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-13 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【湘教版数学九年级上册同步练习】
第二章一元二次方程综合检测题
一、单选题
1.方程x2-2x=0的根是( )
A.x1=0,x2=2 B.x1=0,x2=-2
C.x=0 D.x=2
2.对于任意的实数m,关于x的方程的根的情况是( )
A.有两个相等的实数根 B.有两个不相等的实数根
C.无实数根 D.无法确定
3.下列方程是一元二次方程的是( )
A. B. C. D.
4.方程(x-1)(x+3)=12化为ax2+bx+c=0的形式后,a,b,c的值分别为( )
A.1,2,-15 B.1,-2,-15
C.-1,-2,-15 D.-1,2,-15
5.如果,那么的值为( )
A.2或-1 B.0或2 C.2 D.-1
二、填空题
6.若 无实数解,则m的取值范围是 .
7.如果关于x的一元二次方程x2﹣6x+c=0(c是常数)没有实根,那么c的取值范围是 .
8.已知一元二次方程的两根为,,则 .
9.已知方程x2﹣10x+24=0的两个根是一个等腰三角形的两边长,则这个等腰三角形的周长为 .
10.解方程: 则方程的两个根是 , .
11.阅读理解:对于 这类特殊的代数式可以按下面的方法分解因式:
理解运用:如果 ,那么 ,
即有 或 ,
因此,方程 和 的所有解就是方程 的解.
解决问题:求方程 的解为 .
三、计算题
12.解方程:
(1)x2﹣9=0
(2)x2+2x﹣1=0.
13.用适当的方法解下列方程.
(1)x2﹣3x+1=0;
(2)(x+4)2=5(x+4);
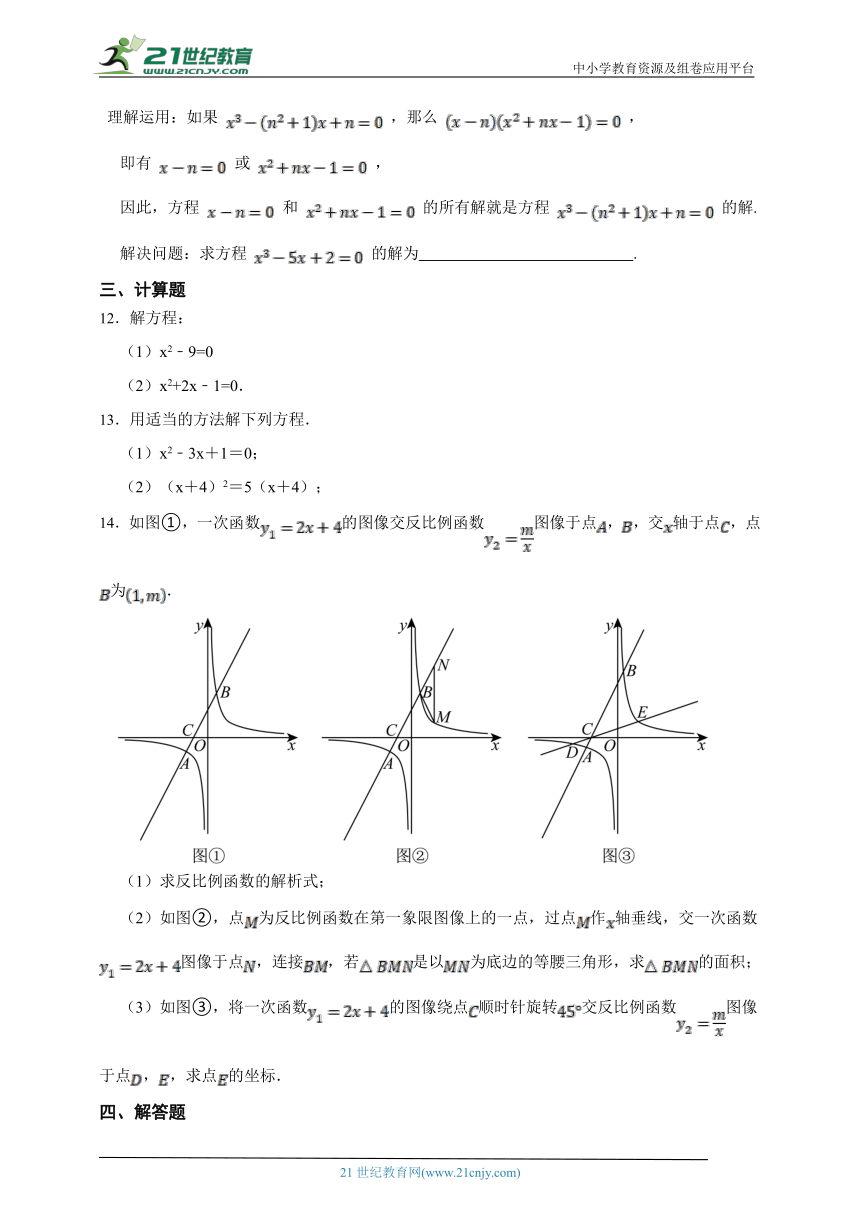
14.如图①,一次函数的图像交反比例函数图像于点,,交轴于点,点为.
(1)求反比例函数的解析式;
(2)如图②,点为反比例函数在第一象限图像上的一点,过点作轴垂线,交一次函数图像于点,连接,若是以为底边的等腰三角形,求的面积;
(3)如图③,将一次函数的图像绕点顺时针旋转交反比例函数图像于点,,求点的坐标.
四、解答题
15.解方程:(1) x2-2x=4
(2)(x+1)2-3(x+1)=0
16.上数学课时,王老师在讲完乘法公式的多种运用后,要求同学们运用所学知识解答:求代数式的最小值?同学们经过交流、讨论,最后总结出如下解答方法:
解:.
,
当时,的值最小,最小值是0.
.
当时,的最小值是1.
请你根据上述方法,解答下列各题:
(1)知识再现:当 时,代数式的最小值是 ;
(2)知识运用:若,当 时,有最 值(填“大”或“小”),这个值是 ;
(3)知识拓展:若,求的最小值.
17.已知: ABCD的两边AB,AD的长是关于x的方程x -mx+ - =0的两个实数根.
(1)当m为何值时,四边形ABCD是菱形 求出这时菱形的边长;
(2)若AB的长为2,那么 ABCD的周长是多少
五、综合题
18.如图是某停车场的平面示意图,停车场外围的长为30米,宽为19米,若停车位总占地面积为390平方米,停车场内车道的宽都相等,求车道的宽.
19.已知关于 的一元二次方程 有两个不相等的实数根.
(1)求 的取值范围;
(2)若 为正整数,求此时方程的根.
20.为进一步改善路容路貌,提升干线公路美化度,某地相关部门初步拟定派一个工程队对一段长度不少于39000米的公路进行路基标准化整修.该工程队以旧设备与新设备交替使用的方式施工,原计划旧设备每小时整修公路30米,新设备每小时整修公路60米
(1)出于保护旧设备的目的,该工程队计划使用新设备的时间比使用旧设备的时间多 ,当这个工程完工时,旧设备的使用时间至少为多少小时?
(2)通过精确的勘察、测测量、规划,以及新增了部分支线公路整修,此工程的实际施工里程比最初拟定的最少里程39000米多了9000米,于是在实际施工中,旧设备在整修公路效率不变的情况下,使用时间比(1)中的最小值多 ,同时,因为工人操作新设备不够熟练,使得得新设备整修公路的效率比原计划下降了 ,使用时间比(1)中新设备使用的最短时间多 ,求a的值.
六、实践探究题
21.已知关于的方程.
(1)若是方程的一个根,求的值和方程的另一根;
(2)当为何实数时,方程有实数根;
(3)若是方程的两个根,阅读材料:设一元二次方程的两根为,则两根与方程系数之间有如下关系:.根据该材料且,试求实数的值.
答案解析部分
1.【答案】A
【知识点】因式分解法解一元二次方程
2.【答案】B
【知识点】一元二次方程根的判别式及应用
3.【答案】A
【知识点】一元二次方程的定义及相关的量
4.【答案】A
【知识点】一元二次方程的定义及相关的量
5.【答案】D
【知识点】零指数幂;因式分解法解一元二次方程
6.【答案】m<-3
【知识点】一元二次方程的根;解一元一次不等式;偶次方的非负性
7.【答案】c>9
【知识点】一元二次方程根的判别式及应用
8.【答案】2
【知识点】一元二次方程的根与系数的关系(韦达定理)
9.【答案】14或16
【知识点】配方法解一元二次方程;三角形三边关系;等腰三角形的性质
10.【答案】2
【知识点】因式分解法解一元二次方程
11.【答案】x=2或 或
【知识点】因式分解法解一元二次方程
12.【答案】(1)解:x2﹣9=0,
∴x2=9,
∴x=±3,
∴x1=3,x2=﹣3
(2)解:x2+2x﹣1=0,
移项得:x2+2x=1,
配方得:x2+2x+1=2,
∴(x+1)2=2,
∴x+1=± ,
∴ x1=﹣1+ ,x2=﹣1﹣ .
【知识点】直接开平方法解一元二次方程;配方法解一元二次方程
13.【答案】(1)解:由x2﹣3x+1=0,
∴ ,
而△=(﹣3)2﹣4×1×1=5>0,
∴x= = ,
解得:x1= ,x2= ;
(2)解:方程移项得:(x+4)2﹣5(x+4)=0,
分解因式得:(x+4)(x+4﹣5)=0,
解得:x1=﹣4,x2=1.
【知识点】公式法解一元二次方程;因式分解法解一元二次方程
14.【答案】(1)
(2)
(3)
【知识点】反比例函数与一次函数的交点问题;三角形全等及其性质;等腰三角形的判定与性质;一元二次方程的应用-几何问题
15.【答案】(1) x=1;(2) x=﹣1或x=2
【知识点】配方法解一元二次方程;因式分解法解一元二次方程
16.【答案】(1)3;3
(2)1;大;
(3)解:,
,
,
,
当时,的最小值为.
【知识点】完全平方公式及运用;配方法的应用
17.【答案】(1)解:∵ 四边形ABCD是菱形
∴AB=AD
∴此方程有两个相等实数根
即b2-4ac=(-m)2-4(-)=0
∴m=1
当m=1时,原方程为x2-x+=0
∴x1=x2=,
即菱形边长为.
即当m=1时,四边形ABCD是菱形,此时边长是.
(2)解:把AB=2代入原方程得:22-2m+-=0
∴m=
又由根与系数关系得:AB+AD=m=
∴AD=-2=
又 ∵平行四边形ABCD
∴AB=CD、BC=AD
∴平行四边形ABCD周长=2(2+)=5。
【知识点】一元二次方程的根;一元二次方程根的判别式及应用;菱形的判定与性质
18.【答案】车道的宽为4米
【知识点】一元二次方程的应用-几何问题
19.【答案】(1)解:∵方程 有两个不相等的实数根,
∴ ,
∴ .
(2)解:∵ 为正整数,且 ,
∴ .
当 时,方程为 ,
∴ , .
【知识点】一元二次方程根的判别式及应用
20.【答案】(1)解:设这个工程完工时,旧设备的使用时间至少为x小时,则新设备的使用时间为 小时,根据题意得
答:当这个工程完工时,旧设备的使用时间至少为300小时
(2)解:由题意得
300×(1+3.2a%)×30+60×(1-a%)×300 × (1+ a%+30%)=39000+9000
原方程化简得
解得 或 ,
∵a﹥0
∴a=
答:a的值是
【知识点】一元二次方程的其他应用;一元一次不等式的应用
21.【答案】(1)解:把代入,得,
解得:,
∴此方程为
根据设方程两根为,则,即,
,
∴方程的另一根是2;
(2)解:①当时,方程是一元一次方程,即,此时的实数解为;
②当时,原方程为一元二次方程,要使方程有实数根,则有,
,
解得:,
即当时,方程有实数根;
(3)解:,
,
整理得,
解得:,
,
;
【知识点】一元二次方程的根;一元二次方程根的判别式及应用;一元二次方程的根与系数的关系(韦达定理)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【湘教版数学九年级上册同步练习】
第二章一元二次方程综合检测题
一、单选题
1.方程x2-2x=0的根是( )
A.x1=0,x2=2 B.x1=0,x2=-2
C.x=0 D.x=2
2.对于任意的实数m,关于x的方程的根的情况是( )
A.有两个相等的实数根 B.有两个不相等的实数根
C.无实数根 D.无法确定
3.下列方程是一元二次方程的是( )
A. B. C. D.
4.方程(x-1)(x+3)=12化为ax2+bx+c=0的形式后,a,b,c的值分别为( )
A.1,2,-15 B.1,-2,-15
C.-1,-2,-15 D.-1,2,-15
5.如果,那么的值为( )
A.2或-1 B.0或2 C.2 D.-1
二、填空题
6.若 无实数解,则m的取值范围是 .
7.如果关于x的一元二次方程x2﹣6x+c=0(c是常数)没有实根,那么c的取值范围是 .
8.已知一元二次方程的两根为,,则 .
9.已知方程x2﹣10x+24=0的两个根是一个等腰三角形的两边长,则这个等腰三角形的周长为 .
10.解方程: 则方程的两个根是 , .
11.阅读理解:对于 这类特殊的代数式可以按下面的方法分解因式:
理解运用:如果 ,那么 ,
即有 或 ,
因此,方程 和 的所有解就是方程 的解.
解决问题:求方程 的解为 .
三、计算题
12.解方程:
(1)x2﹣9=0
(2)x2+2x﹣1=0.
13.用适当的方法解下列方程.
(1)x2﹣3x+1=0;
(2)(x+4)2=5(x+4);
14.如图①,一次函数的图像交反比例函数图像于点,,交轴于点,点为.
(1)求反比例函数的解析式;
(2)如图②,点为反比例函数在第一象限图像上的一点,过点作轴垂线,交一次函数图像于点,连接,若是以为底边的等腰三角形,求的面积;
(3)如图③,将一次函数的图像绕点顺时针旋转交反比例函数图像于点,,求点的坐标.
四、解答题
15.解方程:(1) x2-2x=4
(2)(x+1)2-3(x+1)=0
16.上数学课时,王老师在讲完乘法公式的多种运用后,要求同学们运用所学知识解答:求代数式的最小值?同学们经过交流、讨论,最后总结出如下解答方法:
解:.
,
当时,的值最小,最小值是0.
.
当时,的最小值是1.
请你根据上述方法,解答下列各题:
(1)知识再现:当 时,代数式的最小值是 ;
(2)知识运用:若,当 时,有最 值(填“大”或“小”),这个值是 ;
(3)知识拓展:若,求的最小值.
17.已知: ABCD的两边AB,AD的长是关于x的方程x -mx+ - =0的两个实数根.
(1)当m为何值时,四边形ABCD是菱形 求出这时菱形的边长;
(2)若AB的长为2,那么 ABCD的周长是多少
五、综合题
18.如图是某停车场的平面示意图,停车场外围的长为30米,宽为19米,若停车位总占地面积为390平方米,停车场内车道的宽都相等,求车道的宽.
19.已知关于 的一元二次方程 有两个不相等的实数根.
(1)求 的取值范围;
(2)若 为正整数,求此时方程的根.
20.为进一步改善路容路貌,提升干线公路美化度,某地相关部门初步拟定派一个工程队对一段长度不少于39000米的公路进行路基标准化整修.该工程队以旧设备与新设备交替使用的方式施工,原计划旧设备每小时整修公路30米,新设备每小时整修公路60米
(1)出于保护旧设备的目的,该工程队计划使用新设备的时间比使用旧设备的时间多 ,当这个工程完工时,旧设备的使用时间至少为多少小时?
(2)通过精确的勘察、测测量、规划,以及新增了部分支线公路整修,此工程的实际施工里程比最初拟定的最少里程39000米多了9000米,于是在实际施工中,旧设备在整修公路效率不变的情况下,使用时间比(1)中的最小值多 ,同时,因为工人操作新设备不够熟练,使得得新设备整修公路的效率比原计划下降了 ,使用时间比(1)中新设备使用的最短时间多 ,求a的值.
六、实践探究题
21.已知关于的方程.
(1)若是方程的一个根,求的值和方程的另一根;
(2)当为何实数时,方程有实数根;
(3)若是方程的两个根,阅读材料:设一元二次方程的两根为,则两根与方程系数之间有如下关系:.根据该材料且,试求实数的值.
答案解析部分
1.【答案】A
【知识点】因式分解法解一元二次方程
2.【答案】B
【知识点】一元二次方程根的判别式及应用
3.【答案】A
【知识点】一元二次方程的定义及相关的量
4.【答案】A
【知识点】一元二次方程的定义及相关的量
5.【答案】D
【知识点】零指数幂;因式分解法解一元二次方程
6.【答案】m<-3
【知识点】一元二次方程的根;解一元一次不等式;偶次方的非负性
7.【答案】c>9
【知识点】一元二次方程根的判别式及应用
8.【答案】2
【知识点】一元二次方程的根与系数的关系(韦达定理)
9.【答案】14或16
【知识点】配方法解一元二次方程;三角形三边关系;等腰三角形的性质
10.【答案】2
【知识点】因式分解法解一元二次方程
11.【答案】x=2或 或
【知识点】因式分解法解一元二次方程
12.【答案】(1)解:x2﹣9=0,
∴x2=9,
∴x=±3,
∴x1=3,x2=﹣3
(2)解:x2+2x﹣1=0,
移项得:x2+2x=1,
配方得:x2+2x+1=2,
∴(x+1)2=2,
∴x+1=± ,
∴ x1=﹣1+ ,x2=﹣1﹣ .
【知识点】直接开平方法解一元二次方程;配方法解一元二次方程
13.【答案】(1)解:由x2﹣3x+1=0,
∴ ,
而△=(﹣3)2﹣4×1×1=5>0,
∴x= = ,
解得:x1= ,x2= ;
(2)解:方程移项得:(x+4)2﹣5(x+4)=0,
分解因式得:(x+4)(x+4﹣5)=0,
解得:x1=﹣4,x2=1.
【知识点】公式法解一元二次方程;因式分解法解一元二次方程
14.【答案】(1)
(2)
(3)
【知识点】反比例函数与一次函数的交点问题;三角形全等及其性质;等腰三角形的判定与性质;一元二次方程的应用-几何问题
15.【答案】(1) x=1;(2) x=﹣1或x=2
【知识点】配方法解一元二次方程;因式分解法解一元二次方程
16.【答案】(1)3;3
(2)1;大;
(3)解:,
,
,
,
当时,的最小值为.
【知识点】完全平方公式及运用;配方法的应用
17.【答案】(1)解:∵ 四边形ABCD是菱形
∴AB=AD
∴此方程有两个相等实数根
即b2-4ac=(-m)2-4(-)=0
∴m=1
当m=1时,原方程为x2-x+=0
∴x1=x2=,
即菱形边长为.
即当m=1时,四边形ABCD是菱形,此时边长是.
(2)解:把AB=2代入原方程得:22-2m+-=0
∴m=
又由根与系数关系得:AB+AD=m=
∴AD=-2=
又 ∵平行四边形ABCD
∴AB=CD、BC=AD
∴平行四边形ABCD周长=2(2+)=5。
【知识点】一元二次方程的根;一元二次方程根的判别式及应用;菱形的判定与性质
18.【答案】车道的宽为4米
【知识点】一元二次方程的应用-几何问题
19.【答案】(1)解:∵方程 有两个不相等的实数根,
∴ ,
∴ .
(2)解:∵ 为正整数,且 ,
∴ .
当 时,方程为 ,
∴ , .
【知识点】一元二次方程根的判别式及应用
20.【答案】(1)解:设这个工程完工时,旧设备的使用时间至少为x小时,则新设备的使用时间为 小时,根据题意得
答:当这个工程完工时,旧设备的使用时间至少为300小时
(2)解:由题意得
300×(1+3.2a%)×30+60×(1-a%)×300 × (1+ a%+30%)=39000+9000
原方程化简得
解得 或 ,
∵a﹥0
∴a=
答:a的值是
【知识点】一元二次方程的其他应用;一元一次不等式的应用
21.【答案】(1)解:把代入,得,
解得:,
∴此方程为
根据设方程两根为,则,即,
,
∴方程的另一根是2;
(2)解:①当时,方程是一元一次方程,即,此时的实数解为;
②当时,原方程为一元二次方程,要使方程有实数根,则有,
,
解得:,
即当时,方程有实数根;
(3)解:,
,
整理得,
解得:,
,
;
【知识点】一元二次方程的根;一元二次方程根的判别式及应用;一元二次方程的根与系数的关系(韦达定理)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
