河北省张家口市宣化区2023-2024学年八年级下学期期末数学试题(含答案)
文档属性
| 名称 | 河北省张家口市宣化区2023-2024学年八年级下学期期末数学试题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 236.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-13 00:00:00 | ||
图片预览




文档简介
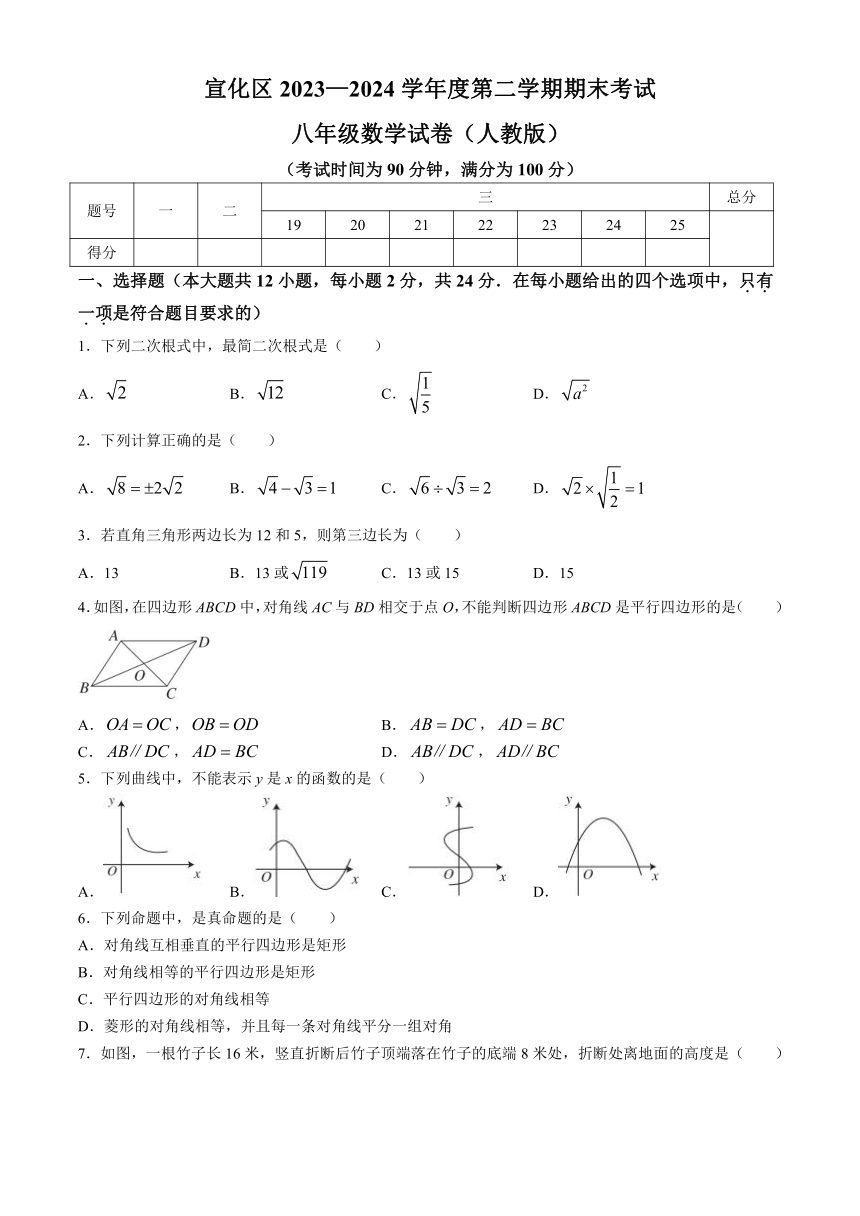
宣化区2023—2024学年度第二学期期末考试
八年级数学试卷(人教版)
(考试时间为90分钟,满分为100分)
题号 一 二 三 总分
19 20 21 22 23 24 25
得分
一、选择题(本大题共12小题,每小题2分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列二次根式中,最简二次根式是( )
A. B. C. D.
2.下列计算正确的是( )
A. B. C. D.
3.若直角三角形两边长为12和5,则第三边长为( )
A.13 B.13或 C.13或15 D.15
4.如图,在四边形ABCD中,对角线AC与BD相交于点O,不能判断四边形ABCD是平行四边形的是( )
A., B.,
C., D.,
5.下列曲线中,不能表示y是x的函数的是( )
A. B. C. D.
6.下列命题中,是真命题的是( )
A.对角线互相垂直的平行四边形是矩形
B.对角线相等的平行四边形是矩形
C.平行四边形的对角线相等
D.菱形的对角线相等,并且每一条对角线平分一组对角
7.如图,一根竹子长16米,竖直折断后竹子顶端落在竹子的底端8米处,折断处离地面的高度是( )
A.6米 B.7米 C.9米 D.10米
8.下表记录了四名同学最近几次一分钟踢毽子选拔赛成绩的平均数与方差.
姓名 甲 乙 丙 丁
平均数 74.25 70 70 65.75
方差 3.07 4.28 2.57 6.78
根据表中数据,要从中选择两名成绩更好且发挥稳定的同学参加正式比赛,应选择( )
A.甲和乙 B.乙和丙 C.甲和丁 D.甲和丙
9.下列说法中不正确的是( )
A.函数的图象经过原点
B.函数的图象位于第二、三、四象限
C.函数的值随x值增大而增大
D.函数的图象不经过第二象限
10.如图,在△ABC中,点D、E、F分别是边AB、AC、BC的中点,要判定四边形DBFE是菱形,下列所添加条件不正确的是( )
A. B. C.BE平分 D.
11.我区某中学刘老师是一名健步走运动的爱好者,她用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),将记录结果绘制成了如图所示的统计图.在每天健步走的步数这组数据中,众数和中位数分别是( )
A.1.2,1.3 B.1.4,1.3 C.1.4,1.35 D.1.3,1.3
12.如图,在平面直角坐标系中,线段AB的端点,.若直线与线段AB有交点,则k的值可能是( )
A.2 B.3 C. D.
二、填空题(本大题共6小题,每小题3分,共18分.把答案写在题中横线上)
13.函数的自变量x的取值范围是______.
14.已知菱形两对角线的长度分别是6cm和8cm,那么菱形的周长______.
15.一组数据3,2,1,4,x的平均数为3,则x为______.
16.已知正比例函数的图象过点,则m的值为______.
17.如图,在△ABC中,于点D,E,F分别为AC,BC的中点,,,,则△DEF的周长是______.
18.如图,直线与直线(k,b为常数,)相交于点,则关于x的不等式的解集为______.
三、解答题(本大题共7小题,共58分)
19.(本小题满分8分)
计算:
20.(本小题满分8分)
如图,在边长为1的小正方形组成的网格中,四边形ABCD的顶点均在格点上.
(1)求证:△ACD是直角三角形;
(2)求四边形ABCD的面积.
21.(本小题满分8分)
如图,菱形ABCD的对角线AC,BD相交于点O,DE垂直平分BC,垂足为点E,求的大小.
22.(本小题满分8分)
某景区有甲、乙两条上山的小路,均由连续的台阶构成,如图所示是甲、乙两路段部分台阶示意图(图中数据表示每一级台阶的高度,单位:cm)
嘉淇的计算 解: .
(1)分别求出两段台阶高度的中位数;
(2)嘉淇计算了甲路段台阶高度的方差,请参照如下她的计算方法,计算乙路段台阶高度的方差,并分析哪段台阶路走起来更舒服?为什么?
23.(本小题满分8分)
如图,一次函数的图象与y轴交于点B,与正比例函数的图象相交于点,且.
(1)分别求出这两个函数的解析式;
(2)求△AOB的面积;
(3)点P在x轴上,且△POA是以OA为腰的等腰三角形,请直接写出点P的坐标.
24.(本小题满分9分)
如图,四边形ABCD的对角线AC、BD交于点O,已知O是AC的中点,,.
(1)求证:;
(2)若,则四边形ABCD是什么特殊四边形?请证明你的结论.
25.(本小题满分9分)
我市某店购进A,B两种雨伞,已知购买A种雨伞30把,B种雨伞40把,共花费2900元,A种雨伞的单价比B种雨伞的单价高15元.
(1)A,B两种雨伞的单价分别是多少元?
(2)商店决定再次购进A,B两种雨伞共50把,正好赶上厂家进行促销活动,促销方式如下:A种雨伞按单价的八折出售,B种雨伞每把降价5元出售,如果此次购买A种雨伞的数量不低于B种雨伞数量的,那么应购买多少把A种雨伞,使此次购买雨伞的总费用最少?最少费用是多少元?
宣化区2023-2024学年度第二学期期末考试
八年级数学试卷参考答案及评分标准(人教版)
一、选择题(本大题有12个小题,每小题2分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 A D B C C B A D C A B D
二、填空题(本大题共6小题,每小题3分,共18分.把答案写在题中横线上)
13.x≥0且x≠2;14.20cm;15.5;16.1;17.14.5;18.x>-1.
三、解答题(本大题共8小题,共58分.解答应写出文字说明、证明过程或演算步骤)
19.解:原式
.
20.解:(1)根据题意得:,,.
.
∴∠ACD=90°,即△ACD是直角三角形.
(2);
∴四边形ABCD的面积为13.
21.解:在菱形ABCD中,有AB=BC=CD=DA,且DC∥AB,
∵DE垂直平分BC,∴BD=DC,
∴BD=BC=DC,
∴△BDC为等边三角形,∴∠DCB=60°,
∵DC∥AB,
∴∠ABC=180°-∠BCD=180°-60°=120°,
答:∠ABC的度数为120°.
22.解:(1)将甲路段台阶的高度从小到大进行排序后,排在中间的两个数为15,15,
∴甲路段台阶高度的中位数为(15+15)÷2=15,
将乙路段台阶的高度从小到大进行排序后,排在中间的两个数为15,17,
∴乙路段台阶高度的中位数为(15+17)÷2=16;
(2)
,
,
,
∵甲、乙路段台阶高度的平均数相等,但甲的方差较小即波动较小,
∴甲路段的台阶走起来更舒服一些.
23.解:(1)∵一次函数的图象与y轴交于点B,与正比例函数的图象相交于点A(4,3),
∴,解得:∴正比例函数的解析式为,
∵A(4,3),∴,
∵OA=OB,∴OB=5,∴点B(0,-5),
把点A(4,3),B(0,-5)代入,得:
,解得:,
∴一次函数的解析式为y=2x-5;
由题意知S△AOB=·OB·∣xA∣=×5×4=10
答:△AOB的面积为10;
(3)点P的坐标为(-5,0)或(5,0)或(8,0).
24.(1)证明:∵DF∥BE,∴∠FDO=∠EBO,∠DFO=∠BEO,
∵O为AC的中点,∴OA=OC,
又∵AE=CF,∴OE=OF,
∴△BOE≌△DOF(AAS);
(2)解:四边形ABCD是矩形,
证明:∵△BOE≌△DOF,∴OB=OD,
又∵OA=OC,∴四边形ABCD是平行四边形,
∵AC=2OA=2OC,又∵AC=2OD,∴OA=OB=OC=OD,即BD=AC,
∴四边形ABCD为矩形.
25.解:(1)设B种雨伞的单价为x元,则A种雨伞的单价为(x+15)元.
30(x+15)+40x=2900,
解得x=35,
∴A种:35+15=50(元)
答:A、B两种雨伞的单价分别是50元、35元.
(2)设购买m把A种雨伞,总费用为W元,
则解得,
∴最小整数解为m=13,
.
∵10﹥0,∴W随m的增大而增大.
∴当m=13时,W取得最小值,最小值为10×13+1500=1630.
答:应购买13把A种雨伞,购买雨伞的总费用最小,最小费用为1630元.
八年级数学试卷(人教版)
(考试时间为90分钟,满分为100分)
题号 一 二 三 总分
19 20 21 22 23 24 25
得分
一、选择题(本大题共12小题,每小题2分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列二次根式中,最简二次根式是( )
A. B. C. D.
2.下列计算正确的是( )
A. B. C. D.
3.若直角三角形两边长为12和5,则第三边长为( )
A.13 B.13或 C.13或15 D.15
4.如图,在四边形ABCD中,对角线AC与BD相交于点O,不能判断四边形ABCD是平行四边形的是( )
A., B.,
C., D.,
5.下列曲线中,不能表示y是x的函数的是( )
A. B. C. D.
6.下列命题中,是真命题的是( )
A.对角线互相垂直的平行四边形是矩形
B.对角线相等的平行四边形是矩形
C.平行四边形的对角线相等
D.菱形的对角线相等,并且每一条对角线平分一组对角
7.如图,一根竹子长16米,竖直折断后竹子顶端落在竹子的底端8米处,折断处离地面的高度是( )
A.6米 B.7米 C.9米 D.10米
8.下表记录了四名同学最近几次一分钟踢毽子选拔赛成绩的平均数与方差.
姓名 甲 乙 丙 丁
平均数 74.25 70 70 65.75
方差 3.07 4.28 2.57 6.78
根据表中数据,要从中选择两名成绩更好且发挥稳定的同学参加正式比赛,应选择( )
A.甲和乙 B.乙和丙 C.甲和丁 D.甲和丙
9.下列说法中不正确的是( )
A.函数的图象经过原点
B.函数的图象位于第二、三、四象限
C.函数的值随x值增大而增大
D.函数的图象不经过第二象限
10.如图,在△ABC中,点D、E、F分别是边AB、AC、BC的中点,要判定四边形DBFE是菱形,下列所添加条件不正确的是( )
A. B. C.BE平分 D.
11.我区某中学刘老师是一名健步走运动的爱好者,她用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),将记录结果绘制成了如图所示的统计图.在每天健步走的步数这组数据中,众数和中位数分别是( )
A.1.2,1.3 B.1.4,1.3 C.1.4,1.35 D.1.3,1.3
12.如图,在平面直角坐标系中,线段AB的端点,.若直线与线段AB有交点,则k的值可能是( )
A.2 B.3 C. D.
二、填空题(本大题共6小题,每小题3分,共18分.把答案写在题中横线上)
13.函数的自变量x的取值范围是______.
14.已知菱形两对角线的长度分别是6cm和8cm,那么菱形的周长______.
15.一组数据3,2,1,4,x的平均数为3,则x为______.
16.已知正比例函数的图象过点,则m的值为______.
17.如图,在△ABC中,于点D,E,F分别为AC,BC的中点,,,,则△DEF的周长是______.
18.如图,直线与直线(k,b为常数,)相交于点,则关于x的不等式的解集为______.
三、解答题(本大题共7小题,共58分)
19.(本小题满分8分)
计算:
20.(本小题满分8分)
如图,在边长为1的小正方形组成的网格中,四边形ABCD的顶点均在格点上.
(1)求证:△ACD是直角三角形;
(2)求四边形ABCD的面积.
21.(本小题满分8分)
如图,菱形ABCD的对角线AC,BD相交于点O,DE垂直平分BC,垂足为点E,求的大小.
22.(本小题满分8分)
某景区有甲、乙两条上山的小路,均由连续的台阶构成,如图所示是甲、乙两路段部分台阶示意图(图中数据表示每一级台阶的高度,单位:cm)
嘉淇的计算 解: .
(1)分别求出两段台阶高度的中位数;
(2)嘉淇计算了甲路段台阶高度的方差,请参照如下她的计算方法,计算乙路段台阶高度的方差,并分析哪段台阶路走起来更舒服?为什么?
23.(本小题满分8分)
如图,一次函数的图象与y轴交于点B,与正比例函数的图象相交于点,且.
(1)分别求出这两个函数的解析式;
(2)求△AOB的面积;
(3)点P在x轴上,且△POA是以OA为腰的等腰三角形,请直接写出点P的坐标.
24.(本小题满分9分)
如图,四边形ABCD的对角线AC、BD交于点O,已知O是AC的中点,,.
(1)求证:;
(2)若,则四边形ABCD是什么特殊四边形?请证明你的结论.
25.(本小题满分9分)
我市某店购进A,B两种雨伞,已知购买A种雨伞30把,B种雨伞40把,共花费2900元,A种雨伞的单价比B种雨伞的单价高15元.
(1)A,B两种雨伞的单价分别是多少元?
(2)商店决定再次购进A,B两种雨伞共50把,正好赶上厂家进行促销活动,促销方式如下:A种雨伞按单价的八折出售,B种雨伞每把降价5元出售,如果此次购买A种雨伞的数量不低于B种雨伞数量的,那么应购买多少把A种雨伞,使此次购买雨伞的总费用最少?最少费用是多少元?
宣化区2023-2024学年度第二学期期末考试
八年级数学试卷参考答案及评分标准(人教版)
一、选择题(本大题有12个小题,每小题2分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 A D B C C B A D C A B D
二、填空题(本大题共6小题,每小题3分,共18分.把答案写在题中横线上)
13.x≥0且x≠2;14.20cm;15.5;16.1;17.14.5;18.x>-1.
三、解答题(本大题共8小题,共58分.解答应写出文字说明、证明过程或演算步骤)
19.解:原式
.
20.解:(1)根据题意得:,,.
.
∴∠ACD=90°,即△ACD是直角三角形.
(2);
∴四边形ABCD的面积为13.
21.解:在菱形ABCD中,有AB=BC=CD=DA,且DC∥AB,
∵DE垂直平分BC,∴BD=DC,
∴BD=BC=DC,
∴△BDC为等边三角形,∴∠DCB=60°,
∵DC∥AB,
∴∠ABC=180°-∠BCD=180°-60°=120°,
答:∠ABC的度数为120°.
22.解:(1)将甲路段台阶的高度从小到大进行排序后,排在中间的两个数为15,15,
∴甲路段台阶高度的中位数为(15+15)÷2=15,
将乙路段台阶的高度从小到大进行排序后,排在中间的两个数为15,17,
∴乙路段台阶高度的中位数为(15+17)÷2=16;
(2)
,
,
,
∵甲、乙路段台阶高度的平均数相等,但甲的方差较小即波动较小,
∴甲路段的台阶走起来更舒服一些.
23.解:(1)∵一次函数的图象与y轴交于点B,与正比例函数的图象相交于点A(4,3),
∴,解得:∴正比例函数的解析式为,
∵A(4,3),∴,
∵OA=OB,∴OB=5,∴点B(0,-5),
把点A(4,3),B(0,-5)代入,得:
,解得:,
∴一次函数的解析式为y=2x-5;
由题意知S△AOB=·OB·∣xA∣=×5×4=10
答:△AOB的面积为10;
(3)点P的坐标为(-5,0)或(5,0)或(8,0).
24.(1)证明:∵DF∥BE,∴∠FDO=∠EBO,∠DFO=∠BEO,
∵O为AC的中点,∴OA=OC,
又∵AE=CF,∴OE=OF,
∴△BOE≌△DOF(AAS);
(2)解:四边形ABCD是矩形,
证明:∵△BOE≌△DOF,∴OB=OD,
又∵OA=OC,∴四边形ABCD是平行四边形,
∵AC=2OA=2OC,又∵AC=2OD,∴OA=OB=OC=OD,即BD=AC,
∴四边形ABCD为矩形.
25.解:(1)设B种雨伞的单价为x元,则A种雨伞的单价为(x+15)元.
30(x+15)+40x=2900,
解得x=35,
∴A种:35+15=50(元)
答:A、B两种雨伞的单价分别是50元、35元.
(2)设购买m把A种雨伞,总费用为W元,
则解得,
∴最小整数解为m=13,
.
∵10﹥0,∴W随m的增大而增大.
∴当m=13时,W取得最小值,最小值为10×13+1500=1630.
答:应购买13把A种雨伞,购买雨伞的总费用最小,最小费用为1630元.
同课章节目录
